Экономико-математическая модель оценки эффективности интеграционных формирований

Автор: Богомолова И.П., Стукало О.Г., Устюгова И.Е.

Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet

Статья в выпуске: 2 (64), 2015 года.

Бесплатный доступ

Оценка эффективности интеграционных формирований требует комплексного подхода, сочетающего использование как количественных, так и качественных показателей. Существующие методы анализа эффективности экономических процессов не могут быть формально применены к задаче выполнения оценки эффективности интеграционных формирований по многим причинам. Применение статистических ретроспективных данных или анализ прецедентов вызывает затруднения вследствие уникальности интеграционных мероприятий и невозможности тиражирования управленческих решений в силу специфичности внутренней среды организаций, нестабильности рынка, действия различных природных факторов, что обусловило необходимость экономико-математического моделирования, экспертных оценок эффективности интеграционных формирований (ЭИФ) с использованием лингвистических переменных и методов теории нечетких чисел. Выбранный математический инструментарий, использованный в предложенной модели - теория нечетких множеств, которые дает возможность анализировать качественные переменные, оперировать нечеткими входными данными и лингвистическими критериями, а так же моделировать сложные системы и сравнивать их между собой. Экономико-математическая модель предусматривает проведение оценки ЭИФ в два этапа. На первом определяются обобщенные оценки каждого из девяти блоков, характеризующих вклад блока в ЭИФ, на втором выполняется интегральная оценка ЭИФ. Заключение об интегральной оценке ЭИФ может быть получено на основе анализа значений комплексных оценок, отражающих результативность блока. Последние учитывают, в свою очередь, что комплексные оценки были получены в результате анализа значений показателей. При этом необходимо обеспечить выполнения требования, чтобы рост значения каждой оценки или показателя был сопряжен с увеличением значения ЭИФ. Это требование выполняется при переходе к лингвистическим значениям. Алгоритмы реализации этапов различаются правилами перехода к лингвистическим переменным - качественным значениям показателей и лингвистическим переменным - оценкам ЭИФ, в остальном алгоритмы идентичны. Представленная экономическо-математическая модель позволяет получить комплексные качественные оценки эффективности интеграционных формирований. Разработанная модель направлена на повышение репрезентативности управленческих решений и снижение рисков интеграционных формирований с учетом отраслевых особенностей мясоперерабатывающей промышленности.

Еще

Интеграция, экономико-математическая модель, мясная промышленность

Короткий адрес: https://sciup.org/14040422

IDR: 14040422

Текст научной статьи Экономико-математическая модель оценки эффективности интеграционных формирований

Оценка эффективности интеграционных формирований требует комплексного подхода, сочетающего использование как количественных, так и качественных показателей. Проведенное исследование подтвердило, что существующие методы анализа эффективности экономических процессов не могут быть формально применены к задаче выполнения оценки эффективности интеграционных формирований по многим причинам. В качестве основных аргументов укажем на то, что прибыль или убытки организации вследствие ее интеграции достаточно трудно оценить, так как сложно прогнозировать объективные результаты как интеграции, так и оценить социально-экономические последствия отказа от нее. Кроме того, использование статистических ретроспективных данных или анализ прецедентов также вызывает затруднения вследствие уникальности интеграционных мероприятий и невозможности тиражирования управленческих решений в силу специфичности внутренней среды организаций, нестабильности рынка, действия различных природных факторов и т.п. Кроме того, многие аспекты интеграции вообще не поддаются количественному измерению, тем более количественному анализу.

Все вышеизложенное обусловило необходимость применения экономико математического моделирования, экспертных оценок эффективности интеграционных формирований с использованием лингвистических переменных и методов теории нечетких чисел. Последовательность проведения экспертного оценивания эффективности интеграционных формирований (ЭИФ) включают следующие этапы:

1. Разработка двухуровневой системы показателей.
2. Определение веса каждого блока в зависимости от степени его значимости – вклада блока в эффективность интеграционных формирований. Определить вес блока можно следующим образом: если веса показателей упорядочены, т.е. имеется информация о том, что Г > 1* 2 > ... > r_n и больше никакой инфор-
,

Первый уровень – уровень блоков. С целью получения репрезентативных оценок выделены девять блоков, в каждом из которых определена система соответствующих показателей (таблица 1).

мации об этих величинах нет, то вес определяется по правилу Фишберна [3]:

r = 2⁽п ^- i + 1 ) , n=9. (1)

¹ (n — 1 )n

Т а б л и ц а 1

Двухуровневая система показателей для оценки ЭИФ

Показатели

1. Блок сырьевого рынка
- 1.1. Структура сырья по видам
- 1.2. Доля отечественного сырья
- 1.3. Доля импортного сырья
2. Блок рынка продаж
- 2.1. Доля рынка реализации
- 2.2. Устойчивость продаж
- 2.3. Ассортимент
3. Финансово экономический блок
4. Блок эффективности интеграционных формирований
5. Социальный блок
6. Инвестиционный блок
7. Инновационный блок
8. Логистический блок
9. Блок качества
3. Назначение веса показателям в каждом блоке, которое выполняется способами, указанными в п. 2.

При условии, что блоки равно предпочтительны или система предпочтений соответствует, то будем считать, что они обладают равным весом:

r_t = 1 / n . (2)

Экономико-математическая модель предусматривает проведение оценки ЭИФ в два этапа.

На первом определяются обобщенные оценки каждого из девяти блоков, характеризующих вклад блока в ЭИФ, на втором выполняется интегральная оценка ЭИФ.

Заключение об интегральной оценке ЭИФ может быть получено на основе анализа значений комплексных оценок, отражающих результативность блока. Последние учитывают, в свою очередь, что комплексные оценки были получены в результате анализа значений показателей. При этом необходимо обеспечить выполнения требования, чтобы рост значения каждой оценки или показателя был сопряжен с увеличением значения ЭИФ. Это требование выполняется при переходе к лингвистическим значениям.

Алгоритмы реализации этапов различаются правилами перехода к лингвистическим переменным – качественным значениям показателей и лингвистическим переменным – оценкам ЭИФ, в остальном алгоритмы идентичны.

Алгоритм может быть представлен следующей последовательностью шагов.

Шаг 1. Определяем общий классификатор для лингвистической оценки значения каждого показателя ЭИФ как разновидность так называемой «серой» шкалы Поспелова [1], представляющей собой полярную (оппозиционную) шкалу, в которой переход от свойства А+ к свойству А- происходит плавно. Шкалы удовлетворяют условиям [2]: взаимной компенсации между свойствами А+ и А- (чем в большей степени проявляется А+, тем в меньшей степени проявляется А-, и наоборот); наличия нейтральной точки А0, интерпретируемой как точка наибольшего противоречия, в которой оба свойства присутствуют в равной степени.

Примем следующие основные обозначения: S - качественная обобщенная оценка ЭИФ;

H - качественная обобщенная оценка блока показателей в смысле вклада блока в оценку ЭИФ;

G - качественная оценка значения показателя.

Значения показателей и оценок ЭИФ будем определять в виде качественных значений - лингвистических переменных.

Шаг 2. Введем лингвистическую переменную s=«значение эффективности интеграционных формирований».

Универсальным множеством для переменной s является отрезок [0,1], а множеством значений переменной s – терм-множество S качественных оценок ЭИФ:

5 = { S 1 , S 2 , S 3 , S 4 , S 5 } , (3)

где S = значение ЭИФ крайне низкое; S = значение ЭИФ ниже среднего; S = значение ЭИФ среднее; S = значение ЭИФ выше среднего; S = значение ЭИФ высокое.

Каждый терм из множества S является именем нечеткого подмножества на отрезке [0,1].

Будем рассматривать эти нечеткие под- множества как трапециевидные нечеткие числа.

Примем, что каждая лингвистическая переменная имеет трапециевидную функцию принадлежности, которая может быть определена четверкой чисел 5 = ( a 1 , a ₂, a ₃, a ₄) , т.е. функция принадлежности каждого терма имеет вид (4).

0, если 5 < a 1 ;

. ^{( 5} ) = -

5 — a,

-------, если a 1 < 5 < a ₂; a ₂ - a 1

1, если a ₂< 5 < a ₃;

5 - a ₄

a ₃ - a ₄

если a ₃< 5 < a ₄ ;

0, если 5 > a ₄.

Составим таблицу функций принадлеж- ности каждого терма (таблица 2).

Т а б л и ц а 2

Функции принадлежности подмножеств терм-множества g

Терм S k	Функции принадлежности нечеткого множества S
Крайне низкое значение ЭИФ S j e [0; 0,25]	Г 1, если 0 < 5 < 0,15; . = ¹ [ 10(0,25 - 5 ), если 0,15 < 5 < 0,25
Значение ЭИФ ниже среднего S ₂ e (0,15; 0,45]	. 2 ='	'1 - 10(0,25 - 5 ), если 0,15 < 5 < 0,25; 1, если 0,25 < 5 < 0,35 10(0,45 - 5 ), если 0,35 < 5 < 0,45
Среднее значение ЭИФ S ₃ e (0,35; 0,65]	" =j	1 - 10(0,45 - 5 ), если 0,35 < 5 < 0,45; 1, если 0,45 < 5 < 0,55 ^ 10(0,65 - 5 ), если 0,55 < 5 < 0,65
Значение ЭИФ выше среднего S ₄ e (0,55; 0,85]	. 4 = <	'1 - 10(0,65 - 5 ), если 0,55 < 5 < 0,65; 1, если 0,65 < 5 < 0,75 10(0,85 - 5 ), если 0,75 < 5 < 0,85
Высокое значение ЭИФ S ₅ e (0,75; 1]	Г 1 - 10(0,85 - 5 ), если 0,75 < 5 < 0,85; . ₅ = ] [ 1, если 0,85 < 5 < 1

Примечание в формулах функций принадлежности не включены интервалы, на которых функция принимает нулевое значение.

Шаг 3. Выполняется для каждого из восьми блоков. Введем лингвистическую переменную h=«значение обобщенной оценки блока показателей в смысле вклада блока в оценку ЭИФ». Как и на шаге 2, универсальным множеством для переменной h является отрезок [0,1], а множеством значений переменной h – терм-множество H качественных оценок результативности блока:

H = { H 1 , H 2 , H 3 , H 4 , H 5 } , ⁽⁵⁾

где H = значение оценки крайне низкое;

H = значение оценки ниже среднего; H = зна- чение оценки среднее; H = значение оценки вы- ше среднего; H = значение оценки высокое.

Каждый терм из множества H является именем нечеткого подмножества на отрезке [0,1]. Также будем рассматривать эти нечеткие подмножества как трапециевидные нечеткие числа h = ( a_x , a ₂, a ₃, a ₄ ), т.е. функция принадлежности каждого терма имеет вид (4).

Шаг 4. Выполняется для каждого показателя в каждом из девяти блоков.

Оценку показателя в смысле его вклада в совокупную оценку блока будем проводить в зависимости от его значения также с использованием лингвистической переменной. Введем лингвистическую переменную g = «значение показателя Х». Универсальным множеством для переменной g является отрезок [n,m], где n – минимальное, m – максимальное значение показателя, а множество значений переменной g – терм-множество G. Примем, что каждая лингвистическая переменная имеет трапециевидную функцию принадлежности, которая определена четверкой чисел g = ( a_x , a ₂, a ₃, a ₄), т.е. функция принадлежности каждого терма G имеет вид (4).

Далее необходимо определить правила перехода от значений показателя Х к значению лингвистической переменной g. При этом, можно выделить три схемы перехода. Ориентируясь на стандартный пятиуровневый классификатор, где функции принадлежности – трапециевидные нечеткие числа (таблица 3), имеем следующие.

Схема 1. Явное экспертное определение значения лингвистической переменной и значения функции принадлежности как степени уверенности эксперта. Сюда можно отнести и балльную оценку по 10 балльной шкале с последующей проекцией балла на классификатор [0; 1].

Схема 2. Если можно определить границы допустимых значений показателя Х, то нормируя достигнутое значение по формуле:

x-xmax x̅ = , xmax-xmin

получаем значение терма и функцию принадлежности в форме (4).

Схема 3. Для каждого терма (значения: низкий, ниже среднего, средний, выше среднего и высокий) следует определить нечеткие интервалы количественных значений, т.е. задать функцию принадлежности g = ( a_x , a_T , a₃ , a ₄ ), а затем определить, в какой интервал попадают достигнутое значение показателя и значение функции принадлежности.

В результате выполнения Шага 4 каждый показатель будет представлен значением лингвистической переменной и значением функции принадлежности.

Шаг 5. Определение лингвистической переменной h=«значение обобщенной оценки блока показателей в смысле вклада блока в оценку ЭИФ». Выполняется для каждого блока.

При выбранной системе весов показателей для каждого из девяти блоков правило перехода от значений показателей к весам термов лингвистической переменной h=«значение обобщенной оценки блока показателей в смысле вклада блока в оценку ЭИФ» имеет вид:

Pk = E r t M ki , ^k = 1,2,3,4,5 , (7) i = 1

где r_i - вес показателя, определяемый по (1) или (2).

Вычислив наблюдаемые веса каждого терма Н i лингвистической переменной, получим значения самой переменной h по формуле:

h = E P k h k , k = 1,2, 3,4,5, ⁽⁸⁾ k = 1

где h k - середина промежутка, который является носителем терма H_k e ( a_kx, a_k ₄].

Шаг 6. Определение лингвистической переменной s=«значение эффективности интеграционных формирований».

При выбранной системе весов, отражающих степень вклада блока в оценку эффективности, правило перехода от значений обобщенных оценок блоков к весам термов лингвистической переменной s=«значение эффективности интеграционных формирований» имеет вид (6).

Вычислив веса каждого терма S i лингвистической переменной, получим значения самой переменной s по формуле:

5 _

5 = ^ P k S k , k = 1,2, 3,4, 5, (9) k = 1

где s k - середина промежутка, который является носителем терма S_k e ( a_k _t, a_k ₄].

Рассмотрим пример реализации экономико-математической модели по объектам исследования.

Шаги с первого по третий определяют классификатор и форму функции принадлежности и имеют общий характер.

Результат выполнения Шага 4 представлены в таблице 3, в которой индекс показателя содержит номер блока (i) и номер показателя в блоке (j) в соответствии с данными таблицы 1. В таблице 3 также отраженно вычисление весов термов лингвистических переменных h i по формуле (6).

Т а б л и ц а 3

Первичная обработка показателей ЭИФ

Показатель		Значения функции принадлежности ^µ ik лингвистической переменной g ij
Х ij	Значение на носителе [0; 1]	Mu	M i 2	^M i3	^M i4	^M i5
1	2	3	4	5	6	7
Х 11	0,82	0	0	0	0,3	0,7
Х 12	0,64	0	0	0,1	0,9	0
Х 13	0,5	0	0	1	0	0
Вес терма лингвистической переменной h 1		0	0	0,367	0,400	0,233
Х 21	0,55	0	0	1	0	0
Х 22	0,3	0	1	0	0	0
Х 23	0,25	0	1	0	0	0
Вес терма лингвистической переменной h 2		0	0,667	0,333	0	0
Х 31	0,58	0	0	0,7	0,3	0
Х 32	0,8	0	0	0	0,5	0,5
Х 33	0,66	0	0	0	1	0
Х 34	0,65	0	0	0	1	0
Х 35	0,82	0	0	0	0,3	0,7
Вес терма лингвистической переменной h 3		0	0	0,140	0,620	0,240
Х 41	0,6	0	0	0,5	0,5	0
Х 42	0,8	0	0	0	0,5	0,5
Х 43	0,3	0	1	0	0	0
Вес терма лингвистической переменной h 4		0	0,333	0,167	0,333	0,167

П р о д о л ж е н и е т а б л. 3

1	2	3	4	5	6	7
Х 51	0,7	0	0	0	1	0
Х 52	0,6	0	0	0,5	0,5	0
Х 53	0,8	0	0	0	0,5	0,5
Х 54	0,68	0	0	0	1	0
Х 55	0,78	0	0	0	0,7	0,3
Х 56	0,4	0	0,5	0,5	0	0
Х 57	0,2	0,5	0,5	0	0	0
Вес терма лингвистической переменной h 5		0,071	0,143	0,143	0,529	0,114
Х 61	0,45	0	0	1	0	0
Х 62	0,35	0	1	0	0	0
Х 63	0,68	0	0	0	1	0
Х 64	0,5	0	0	1	0	0
Вес терма лингвистической переменной h 6		0	0,250	0,500	0,250	0
Х 71	0,7	0	0	0	0,5	0,5
Х 72	0,7	0	0	0	0,5	0,5
Х 73	0,85	0	0	0	0	1
Х 74	0,45	0	0	1	0	0
Вес терма лингвистической переменной h 7		0	0	0,250	0,250	0,500
Х 81	0,55	0	0	1	0	0
Х 82	0,45	0	0	1	0	0
Х 83	0,65	0	0	0	1	0
Вес терма лингвистической переменной h 8		0	0	0,667	0,333	0
Х 91	0,65	0	0	0	1	0
Х 92	0,85	0	0	0	0	1
Х 93	0,7	0	0	0	1	0
Вес терма лингвистической переменной h 9		0	0	0	0,667	0,333

Т а б л и ц а 4

Вычисление значений лингвистических переменных h i =«значение обобщенной оценки блока показателей в смысле вклада блока в оценку ЭИФ» (для первых трех подробно)

Вес терма p лингвистической переменной h i ^*	Множество-носитель k-го терма лингвистической переменной h	Середина промежутка H k , h k	h_k = p_kh k
1	2	3	4
Вес p 1 =0	H e [0; 0,25]	0,125	0
Вес p 2 =0	H ₂ e (0,15; 0,45]	0,3	0
Вес р 3 =0,367	H ₃ e (0,35; 0,65]	0,5	0,1835
Вес p 4 =0,400	H ₄ e (0,55; 0,85]	0,7	0,2800
Вес p 5 =0,233	H ₅ e (0,75; 1]	0,875	0,2039
5 _ ^h1 = T P k h k k = 1			0,6674
Вес p 1 =0	H ₁ e [0; 0,25]	0,125	0
Вес p 2 =0,667	H ₂ e (0,15; 0,45]	0,3	0,2001
Вес р 3 =0,333	H e (0,35; 0,65]	0,5	0,1665
Вес p 4 =0	H e (0,55; 0,85]	0,7	0
Вес p 5 =0	H ₅ e (0,75; 1]	0,875	0
5 _ h 2 = E P k h k k = 1			0,3666

П р о д о л ж е н и е т а б л. 4

1	2	3	4
Вес p 1 =0	H 1 e [0; 0,25]	0,125	0
Вес p 2 =0	H ₂ e (0,15; 0,45]	0,3	0
Вес р 3 =0,140	H ₃ e (0,35; 0,65]	0,5	0,070
Вес p 4 =0,620	H ₄ e (0,55; 0,85]	0,7	0,434
Вес p 5 =0,240	H ₅ e (0,75; 1]	0,875	0,210
5 _ h 3 = Z P k^hk к = 1			0,7140
h ₄			0,5626
^h 5			0,5993
^h 6			0,5000
h			0,7375
^h 8			0,5666
h ₉			0,7583

^* См. итоговые строки таблицы 3

Шаг 5. Выполняется для каждого блока. Определение лингвистической переменной h=«значение обобщенной оценки блока показателей в смысле вклада блока в оценку ЭИФ».

Вычислим значение функции принадлежности лингвистической переменной h=«значение обобщенной оценки блока показателей» по формуле (7) и с учетом весов, определенных в таблице 3. Полученные результаты по девяти блокам представлены в таблице 4 , где подробно показан расчет по первым трем блокам, а для остальных отражен только результат.

Шаг 6. Определение лингвистической переменной s=«значение эффективности интеграционных формирований».

Используя данные таблицы 1, найдем значения функций принадлежности Ц к ( h ) . Например, для первого блока показателей (Блок сырьевого рынка), если h 1 =0,6674, то по формуле (4) и информации таблицы 2: для H 4 =«значение оценки выше среднего»

ц ₄(0,6674) = 1,0

Ц _к (0,6674) =0 для к = 1, 2, 3,5.

Если h 2 =0,3666, то по формуле (4) и информации таблицы 2:

для H =« значение оценки ниже среднего»: ц ₂(0,3666) = 10 - (0,45 - 0,3666) = 0,834 H =« значение оценки среднее»:

ц ₃ (0,3666) = 1 - 10 - (0,45 - 0,3666) = 0,166 ц _к (0,3666) =0 для к = 1, 4, 5 .

Если h 3 =0,7140, то: для H 4 =«значение оценки выше среднего»:

^ 4 (0,7140) = 1 , и ц _к (0,7140) =0

для к = 1, 2,3, 5 .

Итоговые результаты представлены в таблице 5.

Т а б л и ц а 5 Функции принадлежности лингвистических переменных h i =«значение обобщенной оценки блока показателей в смысле вклада блока в оценку ЭИФ»

Лингвистическая переменная		Значения функции принадлежности ^µ ik лингвистической переменной h i
^hi	Значение на носителе [0; 1]	^t 1	Ц - 2	^Ц 3	^Ц 4	Ц 5
^h 1	0,6674	0	0	0	1,0	0
^h - 2	0,3666	0	0,834	0,166	0	0
^h 3	0,7140	0	0	0	1,0	0
h ₄	0,5626	0	0	0,874	0,126	0
^h5	0,5993	0	0	0,507	0,493	0
^h 6	0,5000	0	0	1,0	0	0
h	0,7375	0	0	0	1,0	0
^h 8	0,5666	0	0	0,834	0,166	0
h ₉	0,7583	0	0	0	0,917	0,083
Вес терма лингвистической переменной s		0	0,0927	0,3757	0,5224	0,0092

В результате, используя информация таблицы 1, найдем значения функций принадлежности M k ⁽ s ) :

для S 3 =« значение ЭИФ среднее»

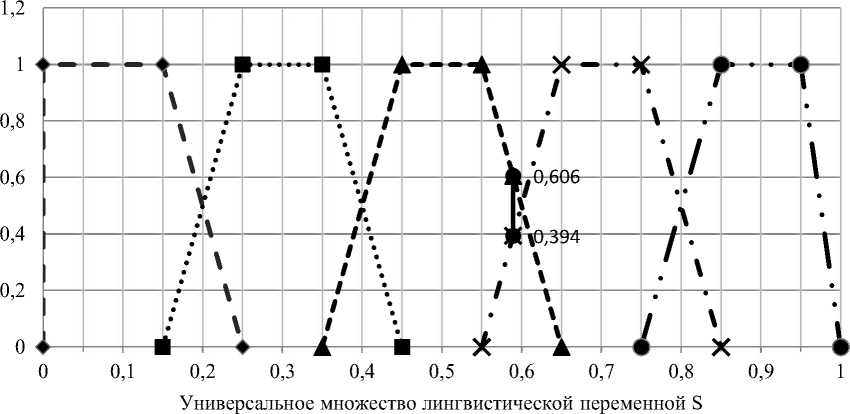
M (0,5894) = 10 • (0,65 - 0,5894) = 0,606

для S 4 =« значение ЭИФ выше среднего»

M ₄ (0,5894) = 1 - 10 • (0,65 - 0,5894) = 0,394 M (0,5894) =0 для к = 1, 2, 5 •

Согласно полученным значениям анализируемых показателей эффективности интеграционных формирований может быть оценена на уровне «значение ЭИФ среднее», что является третьим уровнем эффективности из пяти возможных. Полученные результаты схематично иллюстрирует рисунок 1.

Вычислим значение функции принадлежности лингвистической переменной s=«значение эффективности интеграционных формирований» по формуле (8) и с учетом значений весов, определенных в таблице 5. Итоговые данный вычисления представлены в таблице 6.

Т а б л и ц а 6

* См. итоговую строку таблицы 5.

Вычисление значения лингвистической переменной s=«значение эффективности интеграционных формирований»

Вес терма p лингвистической переменной s i	Множество-носитель k-го терма лингвистической переменной s	Середина промежутка S k , s k	s_k = p_ks k
Вес p 1 =0	S t е [0; 0,25]	0,125	0
Вес p 2 =0,0927	S ₂ е (0,15; 0,45]	0,3	0,0278
Вес р 3 =0,3757	S ₃ е (0,35; 0,65]	0,5	0,1879
Вес p 4 =0,5224	S ₄ е (0,55; 0,85]	0,7	0,3657
Вес p 5 =0,0092	S 5 е (0,75; 1]	0,875	0,0081
s	5 _ = ∑ p_ks k к = 1		0,5894

ЭИФ низкая ЭИФ ниже среднего

Значение ЭИФ среднее ЭИФ выше среднего

Самый высокий уровень ЭИФ Расчетные значения

Рисунок 1. Функции принадлежности лингвистической переменной "оценка эффективности инвестиционных формирований"

Таким образом, выбранный математический инструментарий, использованный в предложенной модели – теория нечетких множеств, потому что использование нечетких множеств, дает возможность анализировать качественные переменные; оперировать нечеткими входными данными и оперировать лингвистическими критериями; моделировать сложные системы и сравнивать их между собой.

Представленная экономическо-математическая модель позволяет получить комплексные качественные оценки эффективности интеграционных формирований. Разработанная модель направлена на повышение репрезентативности управленческих решений и снижение рисков интеграционных формирований с учетом отраслевых особенностей мясоперерабатывающей промышленности.

Список литературы Экономико-математическая модель оценки эффективности интеграционных формирований

Недосекин А.О. Применение теории нечетких множеств к задачам управления финансами//Аудит и финансовый анализ. 2010. № 2.
Конышева Л.К., Назаров Д.М. Основы теории нечетких множеств. СПб: Питер, 2011. 192с.
Богомолова И.П., Стукало О.Г., Устюгова И.Е. Методические подходы к оценке эффективности функционирования интеграционных формирований//Вестник ВГУИТ. 2014. № 1 (59).

Статья научная