Экономико-математическая модель решения логистических задач бизнес-процессов в технологических системах

Большинство предприятий объективно расставляют приоритеты в маркетинге, и продажи находятся на переднем крае бизнеса, однако логистические потери часто приводят к финансовым потерям. Таким образом, своевременное наведение порядка в логистических подразделениях позволяет организовать точность учета, тем самым повысить приоритет предприятия на рынке поставщиков и покупателей [1, 2].

Основными стратегическими задачами логистики являются: оптимизация логистических затрат; оптимизация маршрута движения автомобиля; сокращение времени обработки заказа; количества сотрудников, работающих в отделе логистики; повышение подотчетности и проведение мониторинга текущих показателей; повышение качества услуг [3, 4].

Большинство специалистов по логистике на вопрос о том, можно ли в программном обеспечении предприятия внедрить систему автоматизированного контроля за эффективным использованием транспортных средств, отвечают утвердительно, поскольку без программного обеспечения при планировании движения даже одной машины количество ошибок и просчетов будет уменьшать выгоду от объема экспортируемых товаров [5, 6].

Предприятия с филиалами, разделенными географически, должны четко и правильно выстраивать маршруты движения транспортных средств. Необходимость быстрой и своевременной доставки сырья (от поставщиков и с собственных складов и перемещения между ними) приводит к повышению качества и скорости производства (товаров), а также привлекательности организации в глазах клиентов и, в конечном итоге, увеличению прибыли. В связи с этим промышленные предприятия сталкиваются с необходимостью повышения качества и скорости работы собственной службы доставки или логистических служб. В обязанности логистики входит расчет оптимального пути, минимизация затрат на доставку, заключение договоров с поставщиками и покупателями, что требует больших временных затрат. Отсюда необходимость решения транспортной проблемы, логистической проблемы для ведения бизнес-процессов при внедрении интегрированных экономических и управленческих систем [7].

Материалы и методы

Транспортная задача относится к классу задач линейного программирования и поэтому обладает всеми качествами задач линейной оптимизации, но в то же время имеет несколько дополнительных полезных свойств, которые позволили разработать специальные методы ее решения [8, 9].

Математическая модель транспортной задачи выглядит следующим образом:

Z ⁽ x ) = £ IL c u x u ^ min.

i = 1 j = 1

Математическое описание полной инвентаризации поставщиков транспортных услуг представляет собой систему равенств: n

^ x _jj = a i , i = 1,..., m.

j = 1

Математическое описание удовлетворения запросов потребителей выражается соотношением:

n

ЕХ» = Ь, j = 1,..., П ij           i j=1

Условие неотрицательности всех переменных задачи имеет вид:

x_y >  0, i = 1,..., m , j = 1,..., n .

Далее необходимо добавить математическое описание общей инвентаризации поставщиков и потребителей с указанием типов задачи. Если происходит равенство, то у нас тип задачи с правильным балансом, и модель закрыта, если не соблюдается, то модель имеет вид:

mn a.=^ j i=1         j=1

Этапы решения транспортных задач методом потенциалов показаны на рисунке 1.

Построение начального опорного решения, применяя метод минимальной стоимости, проверка правильности его построения по количеству занятых клеток (m+n-l)

Проверка выполнения необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводится фиктивный поставщик или потребитель с недостающими запасами или запросами и нулевыми стоимостями перевозок

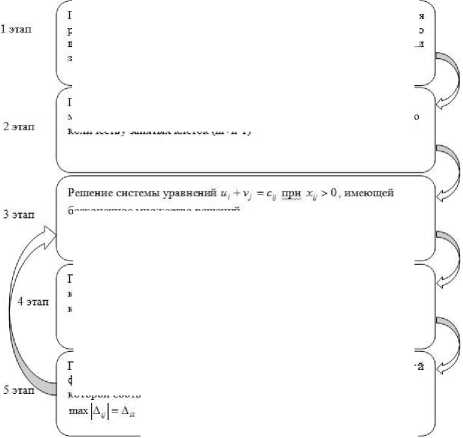
Рисунок 1. Этапы решения транспортных задач методом потенциалов

Figure 1. Stages of solving transport problems by the method of potentials

эесконечное множество решении

Проверить выполнаше условия оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формулам: Д^ — и, + v^ —с^

Перейти к новому опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка:

Для решения транспортной задачи мы решили отойти от классических методов ее решения из-за огромного количества параметров, которые необходимо учитывать при решении задачи и обратились к методам кластерного анализа, позволяющим выявить наиболее значимые факторы, определяющие движение транспортных средств и упрощающие постановку транспортной задачи [10, 11].

Кластерный анализ – это многомерная статистическая процедура, которая выполняет сбор данных, содержащих информацию о выборке объектов, а затем «собирает» объекты в относительно однородные группы. Алгоритм k-средних работает итеративно, чтобы назначить каждую точку данных одной из k групп. Точки данных группируются на основе сходства объектов [12, 13]. Результаты кластеризации алгоритма k-средних получаются из алгоритма:

• • необходимо получить центроиды k кластеров, которые можно использовать для маркировки новых данных;

• •    получить метки для обучающих данных.

Перед проведением процедуры анализа данных, их кластеризация позволяет найти и проанализировать правильно сформированные группы объектов. Каждый центроид кластера – это набор объектов, которые определяют результат группы. Изучение весов центроидов может быть использовано для качественной интерпретации того, что группа представляет единый кластер.

Алгоритм кластеризации k-means включает:

• • общие бизнес-кейсы, в которых мы используем k-means;

• •    шаги, связанные с выполнением алгоритма;

• •    использование данных для доставки.

Алгоритм кластеризации используется для поиска групп, которые не были явно отмечены в данных. Это можно использовать для подтверждения бизнес-предположений о том, какие типы данных существуют, или для идентификации неизвестных групп в сложных наборах данных [14-16]. После запуска алгоритма и определения групп данных любые новые данные можно легко перевести в нужную группу.

Это универсальный алгоритм, который можно использовать для группировки данных любого типа, как показано на рисунке 2.

Кроме того, этот алгоритм поддерживает возможность мониторинга, если отслеживаемые точки данных меняются между группами с течением времени, а также может использоваться для обнаружения значительных изменений в наборе данных [17-19].

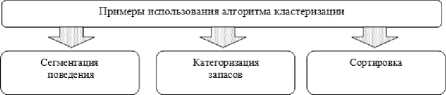
поставщиков

- определение групп «добросовестных»

- сегмент по истории покупок;

- сегмент по видам деятельности в

- групповые запасы пс операциям продажи;

- групповая инвентаризация по произв о дственным метрикам

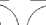
или на платформе:.

- определение персон на основе интересов

Рисунок 2. Примеры использования алгоритма кластеризации k-средних

Figure 2. Examples of using the k-means clustering algorithm

Результаты

В алгоритме кластеризации k-средних мы использовали итеративное уточнение для получения окончательного результата. Для кластеризации входными данными были: количество кластеров k и набор данных. Набор данных состоял из набора объектов для каждой точки данных. Алгоритм начинается с начальных оценок k центроидов, которые случайным образом выбираются из набора данных. Затем алгоритм был разбит на два шага, показанных на рисунке 3.

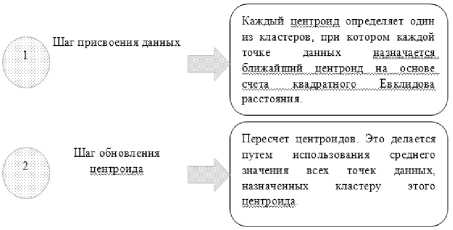
Рисунок 3. Алгоритм кластерного анализа методом k-средних

Figure 3. Algorithm for k-means cluster analysis

Алгоритм повторяется между шагами один и два до тех пор, пока не будет остановлен. Критерий остановки: никакие точки данных не изменят кластеры, сумма расстояний сведена к минимуму, или не будет достигнуто некоторое максимальное количество итераций.

Гарантированная сходимость этого алгоритма приводит к результату, необходимому при ведении технологических процессов. Результатом может быть локальный оптимум (т.е. не обязательно наилучший возможный результат), что означает, что оценка более чем одного прогона алгоритма с рандомизированными начальными центроидами может дать лучший результат.

Одним из показателей, который мы использовали для сравнения результатов для различных значений k - средних, было расстояние между точками данных и их центроидами кластера.

Рассмотрим эволюцию решений транспортной задачи и проследим ее движение от простого к сложному. Уже с появлением двух поставщиков, находящихся в разных уголках страны, возникнут первые трудности в решении транспортной проблемы. Необходим расчет и сравнение нескольких вариантов предотвращения ненужной перевозки на дальние расстояния, выполняемый с использованием экономикоматематического моделирования и компьютерных технологий.

Для формирования маршрутного листа требуется построить маршрут движения автомобиля. В свою очередь, для построения маршрута необходимо проверить грузоподъемность доставляемых товаров в имеющихся транспортных средствах. Если товар не помещается в автомобиле, необходимо разделить существующие точки доставки на группы или кластеры. Каждый кластер элементов имеет общую характеристику, а именно близость расстояния по отношению друг к другу. Для кластеризации используется механизм k-средних, встроенный в технологическую платформу «1С: Предприятие 8.3» [20].

После проведения кластеризации на выходе формируются два кластера, из которых выбирается тот, у которого общий вес доставляемых товаров минимален. После выбора кластера вводятся весогабаритные параметры доставляемых товаров и выполняется итерация по имеющимся транспортным средствам в случае заполнения всех имеющихся товаров. Далее точку доставки из выбранного кластера нужно выстроить в том порядке, в котором будет осуществляться доставка товара. Для этого воспользуйтесь математическим методом до ближайшего соседа. От точки расположения склада производится поиск ближайшего кластера к конечным точкам. Если масса или габариты поставляемого товара превышают грузоподъемность транспортного средства, баллы добавляются в список до тех пор, пока стоимость товара не превышает заложенные в алгоритм параметры. При добавлении баллов в переменные записывается сумма масс доставленных товаров и их габариты. После формирования отгрузочной ведомости формируется маршрутная квитанция, в которую заносится информация о доставленном товаре, его количестве и адресе доставки.

Алгоритм использования метода кластеризации представлен на рисунке 4.

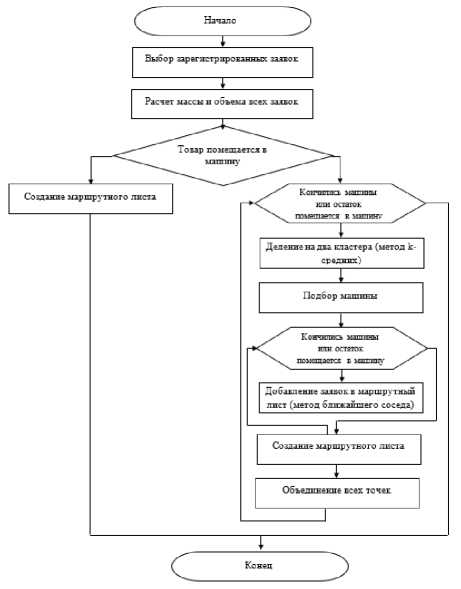
Рисунок 4. Алгоритм процесса заполнения заявки на доставку с помощью кластерного анализа Figure 4. Algorithm of the process of filling out a delivery request using cluster analysis

Заключение

С внедрением автоматизированной системы управления транспортировкой грузов при проведении бизнес-процессов в организациях появится возможность в любой момент получать актуальную картину выполнения заказов клиентов, позволит логистам оптимально управлять доставкой грузов на предприятия. Функциональные возможности автоматизированной системы управления логистическими процессами показаны на рисунке 5.

Рисунок 5. Функциональные возможности автоматизированной системы управления логистикой

Figure 5. Functionality of the automated logistics management system

Информационный поток напрямую контролирует как финансовый поток, так и физическое движение товаров. Информация является неотъемлемым и решающим фактором эффективности управления логистикой, а задачи повышения прозрачности логистической деятельности, ее гибкости и эффективности становятся приоритетными для бизнеса.

Бизнес-возможности по внедрению интегрированных информационных и управленческих систем представлены на рисунке 6.

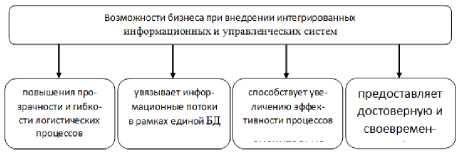
Рисунок 6. Возможности бизнеса при внедрении интегрированных информационных и управленческих систем

Figure 6. Business opportunities in the implementation of integrated information and management systems

Таким образом, метод кластеризации может быть использован для решения транспортной задачи. Построение реальных маршрутов и сравнение их с запланированными закрывает целый ряд проблем. Это дает руководителю гарантию добросовестности персонала и дает возможность корректировать коэффициенты и начальные условия, заданные программой для расчета. Если у руководителя среднее время погрузки и разгрузки товаров больше, чем ожидалось, или некоторые дороги, включенные в маршрут, закрыты, то их нужно исключить из маршрутов. В результате у нас есть удобный мониторинг работы в транспортной логистике предприятия за счет возможности сравнения запланированного маршрута и фактических данных. Руководитель видит фактический маршрут и пробег автомобиля. Информация о опозданиях и отклонениях от маршрута отображается на карте.

Ведение стабильных и понятных бизнес-процессов компанией, предоставление актуальных данных о состоянии заказов и загруженности ресурсов, восстановление порядка в документах, а также оптимизация взаимодействия между отделами – ощутимое повышение эффективности логистики предприятия.

Благодаря автоматическому учету этих и других параметров построенные маршруты будут оптимальными. По опыту наших предприятий-партнеров, это экономит до 20% транспортных расходов.

Подсистема управления логистикой распределяет работу таким образом, чтобы исполнители прибывали в места назначения в удобных для получателя окнах доставки. Система распределяет работу и рассчитывает время прибытия с учетом множества факторов: требований к транспортному средству и его типу, информации об исторических пробках, особенностях и условиях работы каждого водителя.

Подсистема «Управление логистикой» в режиме реального времени отслеживает процесс доставки и при появлении нового заказа анализирует текущее местонахождение и загруженность персонала. На основе этой информации система предлагает наиболее подходящего подрядчика и вносит изменения в маршрут движения.