Экономико-статистическое моделирование производственных процессов в регионах Арктической зоны Российской Федерации

DOI:

Экономико-статистическое моделирование явлений и процессов в региональных системах составляет важное направление исследований в рамках региональной экономики. Очевидно, что это связано с насущной необходимостью в изучении количественной стороны региональных явлений и процессов, обусловленных их качественными характеристиками, познании закономерностей общественного развития, количественной оценке взаимосвязей экономических явлений и процессов, обоснованном прогнозе развития региональных систем. О недостатках и ограничениях применения моделирования к реальным данным, в том числе регионального уровня, говорится значительно меньше. Однако ряд исследователей, включая авторов настоящей статьи, посвятил серию публикаций обсуждению этого вопроса

[1, с. 9–14, 59–65; 2–7]. Полагаем, такие публикации были полезны читателю, в том числе и потому, что, как справедливо указывает Новосельцев В.Н. и Новосельцева Ж.А., «кроме ошибок самого метода моделирования существуют и ошибки, связанные с квалификацией исследователей. Они не свойственны моделям как таковым, а являются, возможно, отражением недостаточного внимания исследователей к создаваемой модели» [8].

Одним из таких недостатков является недоучёт специфики протекания реальных экономических процессов, вызванных не столько внутрирегиональными факторами функционирования региональной системы, сколько внешним управляющим воздействием, которое столь существенно искажает поведение системы и её компонентов, что затрудняет и/или делает невозможным применение типовых экономико-статистических моделей, хорошо работающих в стандартных экономических региональных системах. Например, наши предшествующие исследования показали, что статистически подтверждённая специфика функционирования экономик регионов Севера и Арктики [9; 10] может ограничивать возможности использования производственных функций (ПФ) в силу разбалансированности поведения основных факторов производства [11; 12].

ПФ, несмотря на их известные ограничения, традиционно широко применяются как исследовательский инструмент не только в научных исследованиях, но также в отечественной и зарубежной практике управления, в том числе в официальных прогнозах развития стран и регионов [13, с. 119–134; 14]. Это связано с тем, что они являются удобным инструментом для анализа и прогноза, отображая связь между физическим объёмом факторов производства и физическим объёмом выпуска в процессе производства товаров или услуг. Также важно, что ПФ, как правило, хорошо «работают» на реальных данных. В связи с этим представляет интерес построение ПФ для регионов АЗРФ с учётом возможных ограничений их использования в ряде регионов АЗРФ. Таким образом, цель исследования — экономикостатистическое моделирование производственных процессов в регионах АЗРФ с помощью инструментария ПФ.

Исходные данные и оценка возможностей построения моделей производственных функций для регионов АЗРФ

Как отмечалось, наши предшествующие исследования показали, что специфика функционирования экономик регионов Севера и Арктики может ограничивать возможности использования ПФ в силу разбалансированности взаимодействия основных факторов производства [11; 12]. Поэтому на предварительном этапе был проведён детальный корреляционнорегрессионный анализ, устанавливающий взаимосвязи в поведении факторов производства в регионах АЗРФ. Для представления общероссийской ситуации рассмотрена и РФ в целом.

В работе использовались следующие данные за 2000–2021 гг.: индекс физического объёма ВРП РФ в постоянных ценах в % к предыдущему году, приведённый к значениям 2000 г.; индекс физического объёма инвестиций в основной капитал (ИОК) в сопоставимых ценах в % предыдущему году, приведённый к значениям 2000 г.; стоимость основных фон- дов (СОФ) на конец года по полной учётной стоимости c учётом степени износа, приведённая к значениям 2000 г. с помощью индекса дефлятора ВВП; степень износа основных (на конец года; в процентах); индексы — дефляторы ВВП; среднегодовая численность занятых в экономике РФ, приведённая к индексному виду относительно 2000 г. (ЧЗ).

Анализ динамики ВРП, инвестиций в основной капитал, стоимости основных фондов и численности занятых за 2000–2021 гг. (рис. 1, 2) показал, что имеются существенные различия в поведении этих показателей. В частности, в ряде регионов (Республика Карелия, Республика Коми, Мурманская область, Красноярский край и Чукотский АО) изменения ВРП и численности занятых демонстрируют противоположную динамику. Для того чтобы количественно охарактеризовать эту особенность, были рассчитаны коэффициенты корреляции Пирсона между ВРП и факторами производства: ВРП и инвестициями в основной капитал, ВРП и стоимостью основных фондов, ВРП и численностью занятых (табл. 1). Исходя из анализа корреляций исследуемые регионы были разбиты на 3 группы.

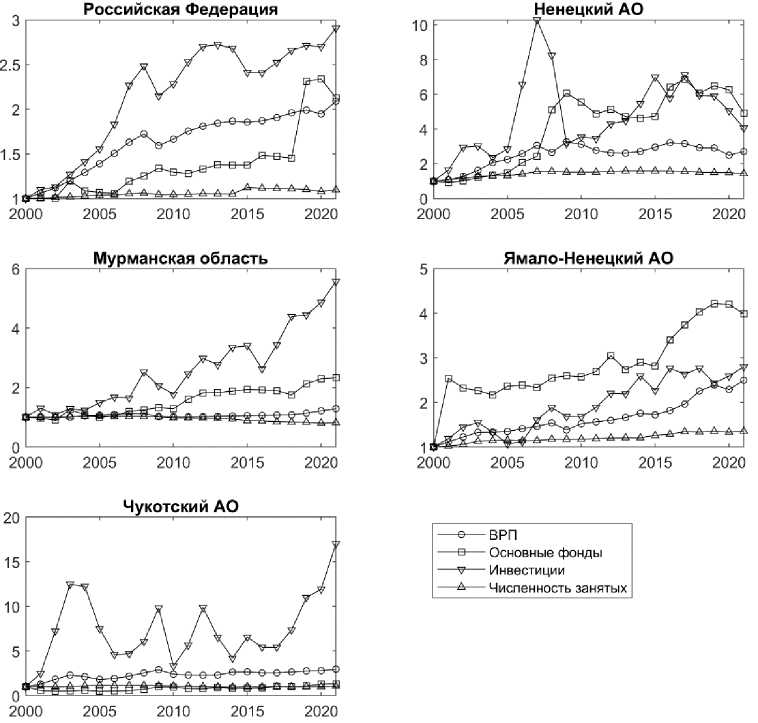
Рис. 1. Динамика факторов производства ВРП за 2000–2021 гг. для всей РФ и регионов, полностью входящих в АЗРФ. Значения показателей (ВРП, стоимость основных фондов, инвестиции в основной капитал, численность занятых) использовались в индексах физического объёма в сопоставимых ценах.

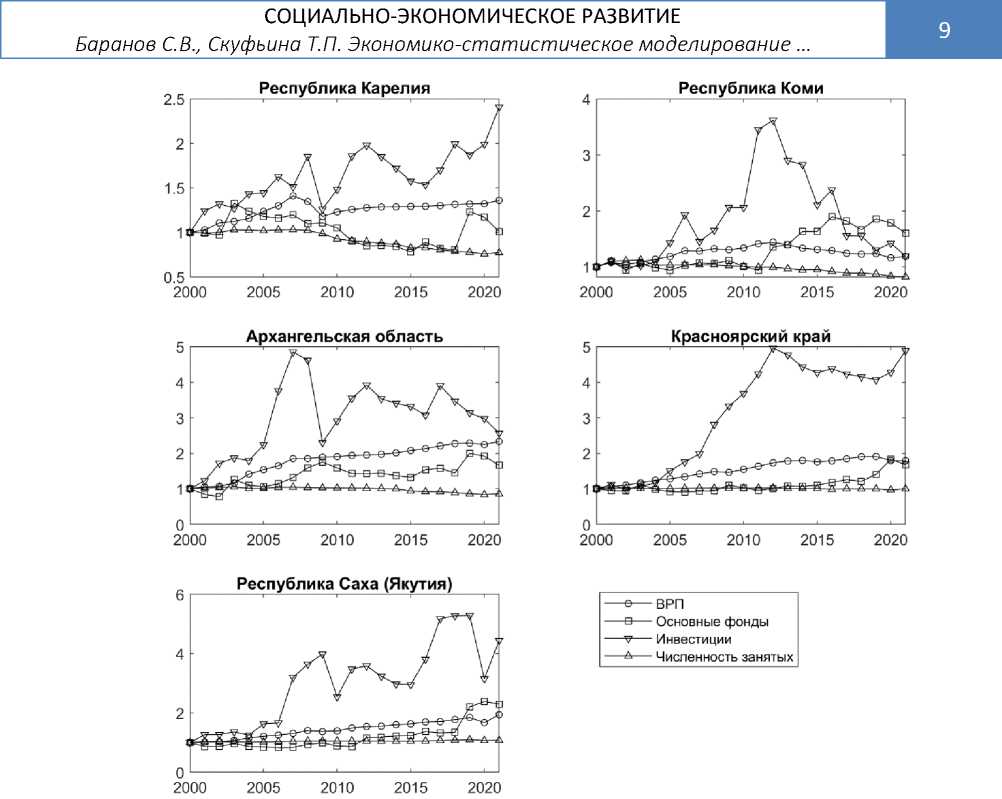
Рис. 2. Динамика факторов производства ВРП за 2000–2021 гг. регионов, частично входящих в АРЗФ. Значения показателей (ВРП, стоимость основных фондов, инвестиции в основной капитал, численность занятых) использовались в индексах физического объёма в сопоставимых ценах.

Таблица 1

Коэффициенты корреляции Пирсона между ВРП и факторами производства за 2000–2021 гг. между ВРП и инвестициями в основной капитал (ИОК), ВРП и стоимостью основных фондов отраслей экономики (СОФ), ВРП и численностью занятых в экономике (ЧЗ) 1

Регион	ВРП-ИОК	ВРП-СОФ	ВРП-ЧЗ	СОФ-ЧЗ	ИОК-ЧЗ
Российская Федерация	0.98	0.73	0.86	0.64	0.77
Полностью в АЗРФ
Мурманская область	0.73	0.56	-0.59	-0.88	-0.90
Ненецкий АО	0.65	0.81	0.93	0.80	0.70
Чукотский АО	0.56	0.54	-0.08	-0.33	0.06
Ямало-Ненецкий АО	0.88	0.94	0.95	0.92	0.89
Частично в АЗРФ
Архангельская область	0.67	0.84	-0.69	-0.62	-0.08
Красноярский край	0.94	0.56	-0.42	-0.81	-0.32
Республика Карелия	0.77	-0.11	-0.49	0.49	-0.69
Республика Коми	0.87	0.18	-0.23	-0.84	-0.13
Республика Саха (Якутия)	0.89	0.75	0.89	0.72	0.91

Группа 1 включает субъекты, в которых взаимное поведение основных факторов производства (труда и капитала) укладывается в общепринятые представления: имеется значимая положительная связь между ВРП и факторами производства. В группу 1 входят: РФ в це-

1 Значения показателей использовались в индексах физического объёма в сопоставимых ценах.

лом, Ненецкий АО, Ямало-Ненецкий АО, Республика Саха (Якутия). Для этих регионов возможно построение классических моделей производства ВРП в виде производственных функций.

Группа 2 — субъекты, в которых взаимное поведение основных факторов производства не укладывается в классические представления: имеется достаточная по силе положительная связь (квадрат коэффициента корреляции не менее 0.6) лишь с одним из факторов производства. Например, ВРП Архангельской области (табл. 1) имеет достаточно значимую положительную связь со стоимостью основных фондов (ВРП-СОФ = 0.84) и отрицательную связь с численностью занятых (ВРП-ЧЗ = -0.69). В группу 2 входят: Архангельская область, Красноярский край, Республика Коми. Для каждого региона из этой группы дополнительно была построена однофакторная модель, в которую был включён фактор, имеющий положительную связь с ВРП.

Группа 3 — субъекты, для которых отсутствует достаточная по силе положительная связь (квадрат коэффициента корреляции менее 0.6) между ВРП и факторами производства. К группе 3 относится Мурманская область, Республика Карелия и Чукотский АО. Для Мурманской области максимальный коэффициент корреляции наблюдается между ВРП и инвестициями в основной капитал ВРП-ИОК = 0.77 (квадрат этого значения равен 0.59). Построение модели производства ВРП для регионов группы 3 по имеющимся факторам производства, которая объясняла бы не менее 60% разброса ВРП невозможно. Использование же модели, которая описывает менее 60% разброса, не является обоснованным с практической точки зрения.

Методика построения моделей

Для каждого региона группы 1 были построены как минимум 4 модели в виде ПФ. Лучшая модель выбиралась с помощью информационного критерия Акаике, скорректированного для малых выборок [15]: чем меньше значение критерия для данного региона, тем лучше модель. Рассматривались Показательная ПФ и ПФ Кобба-Дугласа.

Показательная ПФ имеет вид:

Y = AC? Li,A,р,q >  0,#(1)

где Y — ВРП, С — капитал, L — труд. A , p, q — оцениваемые параметры. Параметры p , q — эластичности по капиталу и труду соответственно; A — общая факторная производительность, характеризует влияние нематериальных факторов, таких как особенности технологии и знаний.

ПФ Кобба-Дугласа является частным случаем показательной ПФ, к которой добавлено ограничение, что сумма эластичностей равна 1:

Y = A&L « ,A,р,q > 0,р + q = 1.#(2)

Для регионов из группы 1 были выполнены оценки параметров ПФ (1) и (2), при этом в качестве капитала C использовались как стоимость основных фондов (СОФ), так и инвестиции в основной капитал (ИОК). Таким образом, для каждого региона из группы 1 были оценены как минимум 4 модели. Если в модели какой-то параметр оказывался незначимым, то модель дополнительно оценивалась без него.

Соответствие модели исходным данным оценивалось по значению скорректированного (по числу параметров модели) коэффициента детерминации Ra ², который отражает процент разброса исходных данных, объясняемый моделью. Если Ra ² не превышает 60%, то модель не использовалась для характеристики экономики исследуемого региона. Отметим, что поскольку ПФ (1) и (2) нелинейные, некорректно выбирать лучшую модель только с помощью Ra ², поэтому дополнительно использовался информационный критерий Акаике.

Для каждой модели было рассчитано значение F -статистики для проверки с помощью F-теста гипотезы о том, что анализируемая модель лучше соответствует исходным данным, чем постоянная величина (константа). Вероятность ошибочного принятия модели вместо константы характеризуется значением p -value, то есть модель является значимой на уровне p -value.

Для каждого параметра моделей были рассчитаны стандартная ошибка ( σ ) и статистика t -value = оценка/ а , чтобы проверить гипотезу о том, что соответствующий параметр равен 0. Уровень незначимости параметра задаётся величиной Pr (> Itl ), то есть если для какого-то параметра Pr (> Itl ) > 0.05, то он является незначимым на 5%-ном уровне. С формальной точки зрения незначимые параметры необходимо исключить из модели, однако в нашем случае параметрами являются производства, и просто исключить труд или капитал из модели нельзя. Например, о каком производстве можно говорить без рабочей силы или основных фондов?

Причины незначимости параметров в регрессионных моделях могут быть разные: например, отсутствие значимой корреляции между независимой и зависимой переменной. Чтобы избежать этого, мы рассчитали коэффициенты корреляции (табл. 1) и отобрали регионы, где имеются значимые корреляции между ВРП и факторами производства. Другой часто встречающейся причиной является высокая мультиколлинеарность (сильная корреляция независимых переменных — факторов производства). Согласно значениям коэффициентов корреляции (табл. 1), эта проблема имеет место для ряда регионов. Например, для Ненецкого и Ямало-Ненецкого АО, Республики Саха (Якутия): присутствует высокая корреляция между стоимостью основных фондов и численностью занятых (СОФ-ЧЗ), а также между инвестициями в основной капитал и численностью занятых (ИОК-ЧЗ). Чтобы учесть влияние этих фактов на производство ВРП (в случае, если это необходимо), были оценены однофакторные модели

Y~ C p , Y= L q , p > 0, q > 0 (~ означает пропорциональность ) (3)

Использование оцениваемого параметра в виде показателя степени в однофакторных моделях (3) обусловлено тем, что это позволяет одинаково интерпретировать параметры с моделями в виде ПФ (1) и (2) как эластичность соответствующего фактора производства. Оценка параметров моделей (1)–(3) выполнялась методом наименьших квадратов после логарифмирования.

Результаты

Рассмотрим результаты моделирования для регионов группы 1. Для РФ в целом (табл. 2) все модели получились статистически значимыми ( p -value < 0.05). Однако для ПФ (2) при C = СОФ (за капитал принята стоимость основных фондов) значение R ² = 0.48, это означает, что модель описывает менее половины разброса исходных данных и должна быть исключена из анализа. При оценивании ПФ (2) при C = ИОК (инвестиции в основной капитал) параметр A оказался незначимым ( Pr (> |t| ) = 0.14), поэтому мы оценили эту модель при A = 1 (log( A ) = 0); оценки приведены в последней строке табл. 2. Для РФ в целом ПФ (1) при C = ИОК оказалась предпочтительнее, чем ПФ (1) при C = СОФ, так как имеет меньшее значение критерия Акаике AICс (табл. 2). В табл. 2 предпочтительные для РФ в целом модели выделены жирным шрифтом. Эти модели объясняют более 97% разброса исходных данных.

Таблица 2 Оценки параметров моделей для РФ в целом по данным за 2000–2021 гг. при использовании в качестве капитала (С) стоимости основных фондов (С = СОФ) и инвестиций в основной капитал (С = ИОК) 2

Параметр	Оценка	σ	t- value	Pr (>| t |)	F	p -value	Ra 2	AICc
ПФ (1), С = СОФ					35.7	3.7E-07	0.77	-32.1
log( A )	0.17	0.04	3.80	1.0E-03
p	0.29	0.13	2.20	4.0E-02
q	3.94	0.93	4.24	4.0E-04
ПФ (1), С = ИОК					1230.0	7.7E-21	0.99	- 105.1
log( A )	0.02	0.01	2.04	5.0E-02
p	0.52	0.02	25.24	4.5E-16
q	1.40	0.20	6.95	1.3E-06
ПФ (2), C = СОФ					20.3	2.2E-04	0.48	-22.2
log( A )	0.27	0.04	6.33	3.5E-06
p	0.60	0.13	4.50	2.2E-04
ПФ (2), C = ИОК					840.0	8.2E-18	0.98	-90.2

2 Жирным шрифтом выделены модели, которые имеют только значимые параметры и объясняют не менее 60% разброса исходных данных. Примечание: оценка — оценённое значение параметра модели; σ — стандартная ошибка оценки параметра; t-value — значение t-статистики; Pr(>|t|) — уровень незначимости параметра; F — F-статистика; p-value — уровень значимость модели; Ra2 — скорректированный коэффициент детерминации; AICc — информационной критерий Акаике.

log( A )	0.02	0.01	1.53	1.4E-01
p	0.60	0.02	28.99	8.2E-18
ПФ (2), A = 1, C = ИОК					867.5	1.5E-18	0.97	-89.5
p	0.62	0.01	69.39	2.7E-26

РФ в целом. Согласно оценкам параметров ПФ (1) при C = ИОК, оценённой для РФ в целом (табл. 2), сумма эластичностей по капиталу и труду ( p + q =1.92) больше 1, что характеризует растущую экономику, то есть каждая единица ресурсов (труда и капитала) используется с большей отдачей. Значение эластичности по ИОК p = 0.52, показывает, что при росте этого фактора производства на 1% ВРП увеличится на 0.52%. Аналогично значение эластичности по численности занятых (ЧЗ) q = 1.4, показывает, что при росте этого фактора производства на 1% ВРП увеличится на 1.4%. Соответствие этой модели, как имеющей наименьшее значение AICc , исходным данным показано на рис. 3. Оценки параметров ПФ (2) при A = 1 и C = ИОК (табл. 2) показывают, что вклад ИОК в производство ВРП составляет 62% ( p = 0.62), а ЧЗ — 38% ( q = 1- p = 0.38).

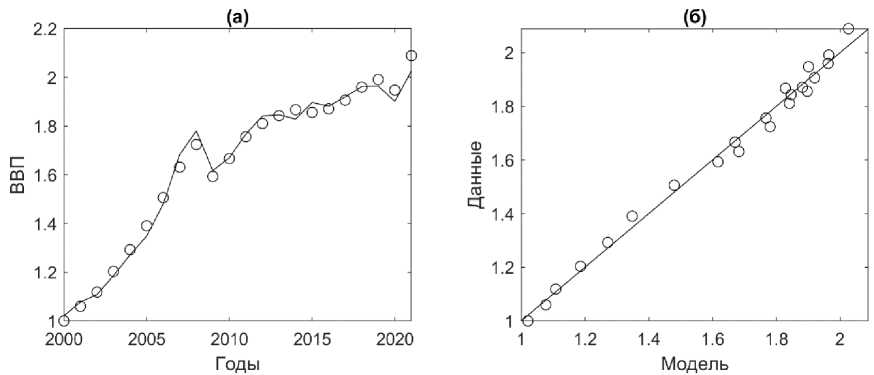
Рис. 3. Соответствие ПФ (1) при использовании в качестве капитала инвестиций в основной капитал ( C = ИОК) исходным данным за 2000–2021 гг. (a) кружки — фактические данные ВРП, чёрная линия — модельные значения, рассчитанные по формуле (1) при A = 1, p = 0.52, q = 1.4 (табл. 2). (б) кружки — фактические данные ВРП, чёрная линия — прямая наилучшего соответствия. Скорректированный коэффициент детерминации Ra ² = 0.99.

Ненецкий АО. Оценки параметров моделей для Ненецкого АО (табл. 3), показывают, что ПФ (1) как при С = СОФ, так и при C =ИОК имеют незначимые параметры А и p , которые должны быть исключены, то есть log( A ) = 0 ( A =1), p = 0. Получившееся модель Y = L^q также была изучена и, согласно оценкам её параметров (табл. 3), при росте ЧЗ на 1% ожидается увеличение ВРП Ненецкого АО на 2.44%. Эта модель лучше остальных соответствует исходным данным для Ненецкого АО (имеет минимальное значение AICc при значимых параметрах). Соответствующая иллюстрация приведена на рис. 4.

Таблица 3

Оценки параметров моделей для Ненецкого АО по данным за 2000–2021 гг. при использовании в качестве капитала (С) стоимости основных фондов (С = СОФ) и инвестиций в основной капитал (С = ИОК) 3

Параметр	Оценка	σ	t-value	Pr(>|t|)	F	p-value	R2	AICc
ПФ (1), С = СОФ					98.3	9.5E-11	0.90	-30.9
log( A )	0.00	0.08	-0.04	9.7E-01
p	0.05	0.07	0.78	4.4E-01
q	2.26	0.37	6.06	7.9E-06
ПФ (1), С = ИОК					95.7	1.2E-10	0.90	-30.4
log( A )	-0.03	0.07	-0.35	7.3E-01
p	-0.03	0.08	-0.37	7.1E-01
q	2.62	0.33	7.83	2.3E-07
ПФ (2), C = СОФ					29.9	2.4E-05	0.58	-19.3
log( A )	0.27	0.05	5.05	6.1E-05
p	0.29	0.05	5.47	2.4E-05
ПФ (2), C = ИОК					13.0	1.8E-03	0.36	-10.2
log( A )	0.16	0.10	1.58	1.3E-01
p	0.32	0.09	3.61	1.8E-03
ПФ: Y = L4					195.3	4.2E-12	0.90	-35.1
q	2.44	0.06	41.06	1.5E-21
ПФ: Y = ACp, C = СОФ					57.3	2.7E-07	0.73	-9.9
log( A )	0.37	0.08	4.92	8.2E-05
p	0.41	0.05	7.57	2.7E-07
ПФ: Y = Cp, C = ИОК					44.8	1.3E-06	0.68	-2.5
p	0.60	0.03	19.15	8.9E-15

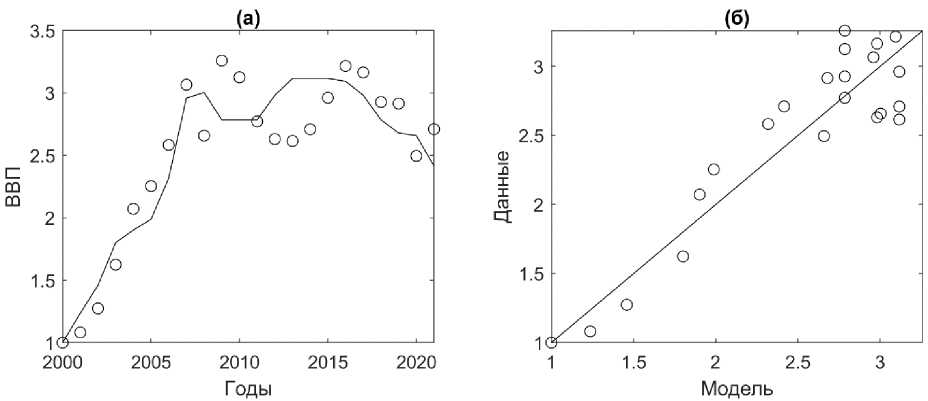
Рис. 4. Соответствие ПФ Y = L^q исходным данным Ненецкого АО за 2000–2021 гг. (a) кружки — фактические данные ВРП, чёрная линия — модельные значения, рассчитанные по формуле (1) при q = 2.44 (табл. 2). (б) кружки — фактические данные ВРП, чёрная линия — прямая наилучшего соответствия. Скорректированный коэффициент детерминации Ra ² = 0.9.

Модели в виде ПФ (2) при C = СОФ и C = ИОК для Ненецкого АО хоть и является статистически значимыми (табл. 3), описывают лишь 58% и 36% разброса исходных данных (соответственно ( Ra ² = 0.58, Ra ² = 0.36)) и поэтому исключены из анализа. Для того чтобы выяснить влияние СОФ на ВРП, была оценена модель ПФ: Y = AC^p при C = СОФ, которая оказалась статистически значимой и объясняет 73% разброса исходных данных (табл. 3). У этой модели эластичность по СОФ p = 0.41, следовательно, при росте этого фактора на 1% ожидаемое увеличение ВРП составляет на 0.41%. Также была оценена модель Y = C^p при C = ИОК (табл. 3). Эта модель значима и объясняет 68% разброса исходных данных (в модели Y = AC^p параметр А оказался незначимым); оценка p = 0.60, то есть рост ИОК на 1% даст увеличение ВРП на 60%.

Ямало-Ненецкий АО. Оценки моделей для Ямало-Ненецкого АО (табл. 4) показывают, что ПФ (1) как при С = СОФ, так и при C =ИОК имеют незначимые параметры А и p , которые должны быть исключены, то есть log( A ) = 0 ( A =1), p = 0. Получившаяся модель Y = L^q также была изучена и, согласно оценкам её параметров, при росте ЧЗ на 1% ожидается увеличение ВРП Ненецкого АО на 2.65%. Эта модель лучше остальных соответствует исходным данным для Ямало-Ненецкого АО (имеет минимальное значение AICc при значимом параметре). Соответствующая иллюстрация приведена на рис. 5.

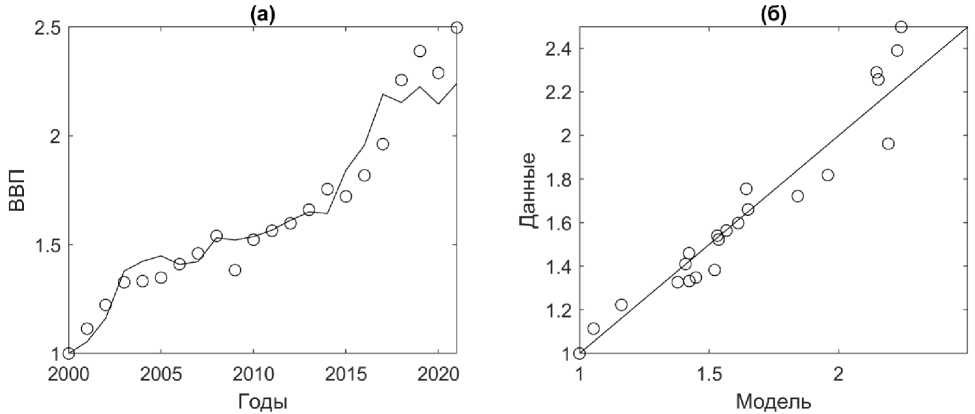
Рис. 5. Соответствие ПФ Y = L^q исходным данным Ненецкого АО за 2000–2021 гг. (a) кружки — фактические данные ВРП, чёрная линия — модельные значения, рассчитанные по формуле (1) при q = 2.65 (табл. 2). (б) кружки — фактические данные ВРП, чёрная линия — прямая наилучшего соответствия. Скорректированный коэффициент детерминации Ra ² = 0.94.

Таблица 4

Оценки параметров моделей для Ямало-Ненецкого АО по данным за 2000–2021 гг. при использовании в качестве капитала (С) стоимости основных фондов (С = СОФ) и инвестиций в основной капитал (С = ИОК) 4

Параметр	Оценка	σ	t -value	Pr(>|t|)	F	p -value	Ra 2	AICc
ПФ (1), С = СОФ					169.0	7.9E-13	0.94	- 57.9
log( A )	-0.07	0.05	-1.52	1.5E-01

4 Обозначения столбцов даны в примечании к табл. 2. Жирным шрифтом выделены модели, которые имеют только значимые параметры и объясняют не менее 60% разброса исходных данных.

p	0.14	0.09	1.65	1.2E-01
q	2.26	0.30	7.46	4.6E-07
ПФ (1), С = ИОК					160.0	1.3E-12	0.94	- 56.7
log( A )	-0.01	0.03	-0.36	7.2E-01
p	0.10	0.08	1.27	2.2E-01
q	2.34	0.31	7.51	4.2E-07
ПФ (2), C = СОФ					35.7	7.7E-06	0.62	- 37.0
log( A )	-0.16	0.08	-2.01	5.8E-02
p	0.54	0.09	5.97	7.7E-06
ПФ (2), C = ИОК					34.1	1.0E-05	0.61	- 36.4
log( A )	0.08	0.04	1.97	6.3E-02
p	0.48	0.08	5.84	1.0E-05
ПФ: Y = L л q					312.8	4.3E-14	0.94	- 60.0
q	2.65	0.07	40.627	1.9E-21
ПФ (2): A = 1, C = СОФ					14.5	1.0E-03	0.57	- 35.4
p	0.36	0.03	13.978	4.2E-12
ПФ (2): A = 1, C = ИОК					50.8	5.0E-07	0.56	- 34.9
p	0.62	0.05	13.81	5.3E-12	14.5	1.0E-03
ПФ: Y = AC, C = СОФ					75.6	3.1E-08	0.78	- 30.5
log( A )	-0.23	0.08	-2.78	1.2E-02
p	0.70	0.08	8.6975	3.1E-08
ПФ: Y = Cp, C = ИОК					89.0	5.3E-09	0.81	- 29.2
p	0.74	0.04	19.80	4.6E-15

Модели в виде ПФ (2) при C = СОФ и C = ИОК для Ямало-Ненецкого АО, хоть и являются статистически значимыми (табл. 4), имеют незначимый параметр A ( Pr (>| t |) > 0.05), который должен быть исключён. Были выполнены оценки ПФ (2) при A =1 C = СОФ и C = ИОК, оказалось, что они объясняют менее 60% разброса исходных данных (табл. 4), потому в дальнейшем анализе использоваться не будут.

Коэффициенты корреляции ВРП-СОФ и ВРП-ИОК для Ямало-Ненецкого АО больше 0.8 (табл. 1), это даёт нам основание отдельно оценить зависимость ВРП от СОФ и ИОК без учёта ЧЗ, то есть в ПФ (1) положить q = 1.Тогда Y = ACp, где капитал C = СОФ или C = ИОК. Советующие оценки приведены в табл. 4 в двух последних строках (при C = ИОК параметр A оказался незначимым и был исключён). Обе модели оказались значимыми и описывают 78 и 81% разброса исходных данных соответственно. Получившееся значение эластичности по СОФ (ИОК) p = 0.7 (p = 0.74) показывает, что при увеличении этого фактора на 1% ожидается рост ВРП на 70% (74%). Несмотря на то, что не удалось построить модель производства ВРП Ямало-Ненецкого АО, которая бы включала как труд, так и капитал, значение коэффициента кор- реляции ИОК-ЧЗ 0.89 (табл. 1) даёт основание оценить зависимость ЧЗ от СОФ и ИОК, которая была приведена ниже.

Республика Саха (Якутия). Оценки моделей для Республики Саха (Якутия) (табл. 5) показывают, что ПФ (1) как при С = СОФ, так и при C =ИОК имеют незначимые параметры А и p , которые необходимо исключить, чтобы избежать смещения оценок эластичностей, то есть log( A ) = 0 ( A =1), p = 0. Получившаяся модель Y = L^q также была изучена. Согласно оценкам (табл. 5), модель объясняет 74% разброса исходных данных, а при росте ЧЗ на 1% ожидается увеличение ВРП Ненецкого АО на 7.49%.

Таблица 5 Оценки параметров моделей для Республики Саха (Якутия) по данным за 2000–2021 гг. при использовании в качестве капитала (С) стоимости основных фондов (С = СОФ) и инвестиций в основной капитал (С = ИОК) 5

Параметр	Оценка	σ	t -value	Pr (>| t |)	F	p -value	Ra 2	AICc
ПФ (1), С = СОФ					39.5	1.7E-07	0.79	-37.6
log( A )	0.01	0.06	0.21	8.4E-01
p	0.14	0.09	1.52	1.4E-01
q	6.69	1.40	4.79	1.3E-04
ПФ (1), С = ИОК					58.1	5.8E+01	0.85	-44.6
log( A )	-0.03	0.04	-0.77	4.5E-01
p	0.24	0.08	3.22	4.5E-03
q	2.91	1.84	1.58	1.3E-01
ПФ (2), C = СОФ					22.2	1.4E-04	0.50	-24.9
log( A )	0.26	0.03	9.26	1.1E-08
p	0.42	0.09	4.71	1.3E-04
ПФ (2), C = ИОК					88.5	8.8E-09	0.81	-45.7
log( A )	-0.01	0.04	-0.20	8.4E-01
p	0.33	0.03	9.41	8.8E-09
ПФ: Y = L					60.0	1.4E-07	0.74	-39.3
q	7.49	0.399	18.80	1.3E-14
ПФ: Y = Cp, C = ИОК					110.6	8.0E-10	0.84	-47.0
p	0.35	0.02	22.59	3.3E-16
ПФ: Y = ACp , C = СОФ					26.7	4.7E-05	0.55	-22.8
log( A )	0.29	0.03	9.22	1.2E-08
p	0.46	0.09	5.17	4.7E-05
ПФ (2), A = 1, C = ИОК					89.3	5.2E-09	0.82	-48.1
p	0.32	0.02	20.12	3.3E-15

ПФ (2) при C =СОФ хоть и является значимой, однако объясняет всего 50% разброса исходных данных и поэтому исключается из дальнейшего анализа. ПФ (2) при C =ИОК имеет незначимый параметр A . Оценка этой модели при A =1 показывает, что модель является статистически значимой, объясняет 82% разброса исходных данных и имеет наименьшее зна-

• ⁵    Обозначения столбцов даны в примечании к табл. 2. Жирным шрифтом выделены модели, которые имеют только значимые параметры и объясняют не менее 60% разброса исходных данных.

чение критерия Акаике AICc =-48.1 (табл. 5) и, следовательно, является наиболее предпочтительной для Республики Саха (Якутия). Оценки параметров этой модели показывают, что вклад в производство ВРП ИОК составляет 32% ( p = 0.32), а ЧЗ 68% ( q = 1 — p = 0.68). Соответствие этой модели исходным данным показано на рис. 6.

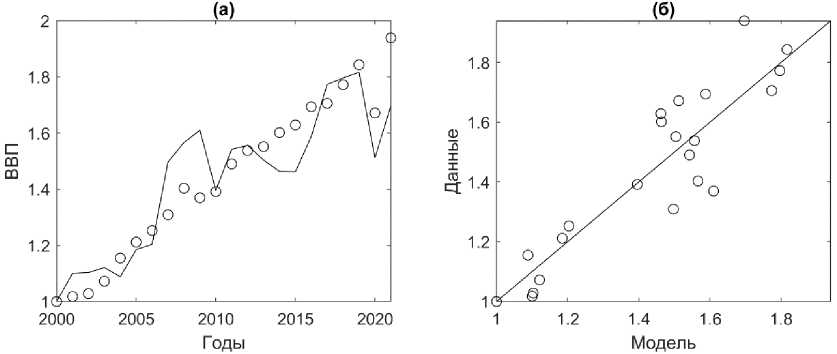
Рис. 6. Соответствие ПФ (2) при C = ИОК исходным данным Республики Саха (Якутия) за 2000–2021 гг. (a) кружки — фактические данные ВРП, чёрная линия — модельные значения, рассчитанные по формуле (2) при A = 1 и p = 0.32 (Табл. 2). (б) кружки — фактические данные ВРП, чёрная линия — прямая наилучшего соответствия. Скорректированный коэффициент детерминации Ra ² = 0.82.

Количественно охарактеризовать влияние капитала на производства ВРП Республики Саха (Якутия) можно по модели Y = C^p , при C = СОФ или при C = ИОК (табл. 5). При C = СОФ оказалась, что эта модель объясняет лишь 55% исходных данных и не может использоваться для анализа. При C = ИОК (модель значима и объясняет 84% разброса исходных данных) ожидается, что рост ИОК на 1% будет сопровождаться ростом ВРП на 35% ( p = 0.35).

Рассмотрим результаты моделирования для регионов группы 2. Для этих регионов построение модели в виде ПФ (1) не имеет смысла, поскольку эластичность одного из факторов производства будет либо статистически незначимой, либо вообще отрицательной. Последнее противоречит экономической теории. Построение модели в виде ПФ (2), напротив, является оправданным и позволяет оценить вклад каждого фактора в производства. Действительно ПФ (2) можно переписать в виде Y / L = A ( C / L ) ^p . Пусть корреляция ВРП-СОФ положительная, а ВРП-ЧЗ отрицательная (например, Архангельская обл.). Тогда корреляция отношений Y / L (ВРП на одного работника) и C / L ( СОФ на одного работника) может оказаться положительной. В этом случае p характеризует вклад СОФ в производство ВРП, а q = 1- p — вклад ЧЗ в производство ВРП. Чем сильнее ЧЗ снижается на фоне роста ВРП, тем больше отношение Y/L и тем сильнее вклад этого фактора.

Архангельская область. Оценки параметров ПФ (2) при С = СОФ показывают (табл. 6), что модель является статистически значимой (p-value < 0.05) и объясняет 80% разброса исходных данных (Ra2 = 0.8). Вклад в производства ВРП СОФ p = = 98%, а ЧЗ q = 1 — p = 2%. Фактически ВРП этого региона не зависит от имеющейся ЧЗ, так как за 2000–2021 гг. ЧЗ постоянно снижалась на фоне постоянного роста ВРП (рис. 2). Оценки параметров ПФ (2) при С = ИОК и A = 1 (оценка параметра A статистически незначима) показывают (табл. 6), что модель ста- тистически значима и объясняет 66% разброса исходных данных. В этой двухфакторной мо дели вклад ИОК в производство ВРП p = = 57%, а ЧЗ q = 1 — p = 43%.

Таблица 6 Оценки параметров моделей для Архангельской области по данным за 2000–2021 гг. при использовании в качестве капитала (С) стоимости основных фондов (С = СОФ) и инвестиций в основной капитал (С = ИОК) 6

Параметр	Оценка	σ	t -value	Pr (>| t |)	F	p -value	Ra 2	AICc
ПФ (2), С = СОФ					84.1	1.3E-08	0.80	-20.5
log( A )	0.27	0.05	5.75	1.3E-05
p	0.98	0.11	9.17	1.3E-08
ПФ (2), A = 1, С = ИОК					35.8	6.1E-06	0.66	-10.2
p	0.57	0.04	15.98	3.2E-13
ПФ: Y = A C, C = СОФ					54.7	3.8E-07	0.72	-20.7
log( A )	0.28	0.05	5.62	1.7E-05
p	0.95	0.128	7.40	3.8E-07
ПФ: Y = C, C = ИОК					41.8	2.1E-06	0.65	-16.9
p	0.55	0.03	17.57	4.9E-14

Для того чтобы количественно охарактеризовать зависимость ВРП от СОФ и ИОК, были оценены однофакторные модели (3). Согласно оценкам (табл. 6), при изменении СОФ на 1% ВРП ожидаемое изменение ВРП составит p = 0.95%, при этом соответствующая модель ( Y ~ C^p ) является значимой и объясняет 72% разброса исходных данных, согласно значению критерия Акаике AICc модель является наилучшей для Архангельской области (рис. 7). При изменении ИОК на 1% ожидаемое изменение ВРП составит p = 0.55%, соответствующая модель ( Y ~ C^p ) является значимой и объясняет 65% разброса исходных данных. Обращает внимание отсутствие корреляции между СОФ и ИОК (табл. 1) для Архангельской области. Это объясняет столь разные значения эластичностей ( p ) по СОФ и ИОК.

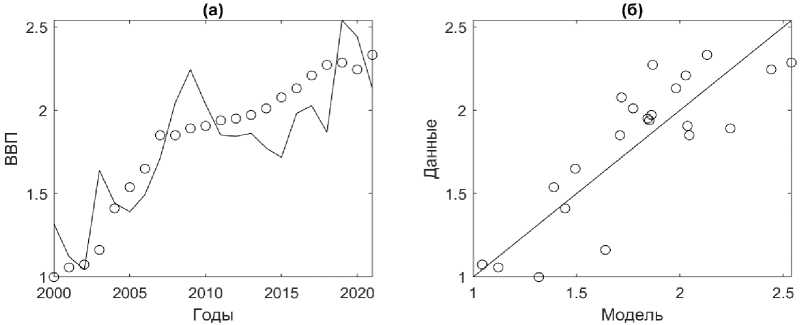
Рис. 7. Соответствие модели Y ~ C^p при C = СОФ исходным данным Архангельской области за 2000–2021 гг. (a) кружки — фактические данные ВРП, чёрная линия — модельные значения, рассчитанные по формуле (3) при A = 1.32 и p = 0.95 (табл. 7). (б) кружки — фактические данные ВРП, чёрная линия — прямая наилучшего соответствия. Скорректированный коэффициент детерминации Ra ² = 0.72.

• ⁶    Обозначения столбцов даны в примечании к табл. 2. Жирным шрифтом выделены модели, которые имеют только значимые параметры и объясняют не менее 60% разброса исходных данных.

Красноярский край. ПФ (2) при С = СОФ описывает лишь 34% разброса исходных данных (табл. 7) и поэтому исключается из анализа. Оценка ПФ (2) при C = ИОК показала, что модель является значимой и описывает 91% разброса исходных данных. Влад ИОК в производство ВРП p = 33%, вклад ЧЗ q = 100 — p = 67%. В этом регионе рост ВРП происходит на фоне практически постоянной ЧЗ: отношение максимального и минимального значений за 2000–2021 гг. составляет 1.06, при этом ВРП практически удвоился за это период, а рост ИОК увеличился в 5 раз по сравнению с базовым 2000 г. (рис. 2). То есть рост ВРП происходит за счёт роста ИОК при фактическом дефиците рабочей силы, потому вклад ЧЗ в ВРП больше вклада ИОК.

Таблица 7 Оценки параметров моделей для Красноярского края по данным за 2000–2021 гг. при использовании в качестве капитала (С) стоимости основных фондов (С = СОФ) и инвестиций в основной капитал (С = ИОК) 7

Параметр	Оценка	σ	t -value	Pr (>| t |)	F	p -value	Ra 2	AICc
ПФ (2), С = СОФ					11.6	2.8E-03	0.34	-12.6
log( A )	0.35	0.04	8.75	2.8E-08
p	0.64	0.19	3.40	2.8E-03
ПФ (2), C = ИОК					211.0	4.3E-12	0.91	-56.4
log( A )	0.08	0.03	3.14	5.2E-03
p	0.33	0.02	14.54	4.3E-12
ПФ: Y = ACp , C = СОФ					9.9	5.1E-03	0.30	-13.1
log( A )	0.35	0.04	8.61	3.7E-08
p	0.62	0.198	3.14	5.1E-03
ПФ: Y = AC, C = ИОК					228.0	2.1E-12	0.92	-59.0
log( A )	0.09	0.02	3.72	1.4E-03
p	0.32	0.02	15.10	2.1E-12

Оценки однофакторных моделей (3) показали (табл. 7) при C = СОФ, что модель Y ~ C^p объясняет лишь 30% разброса исходных данных и, следовательно, не может использоваться в дальнейшем анализе. Модель Y ~ C^p при ф = ИОК является значимой и объясняет 92% разброса исходных данных; при изменении ИОК на 1% ожидаемое увеличение ВРП составит 0.32%. Согласно значениям критерия AICc , эта модель лучше всего соответствует исходным данным (рис. 8).

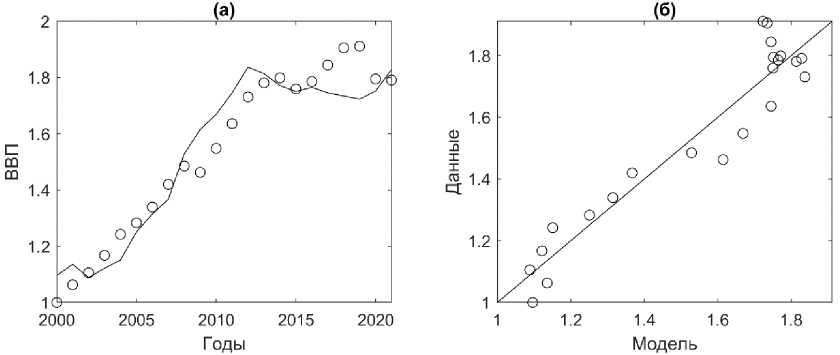
Рис. 8. Соответствие модели Y ~ C при C = ИОК исходным данным Красноярского края за 2000-2021 гг. (a) кружки — фактические данные ВРП, чёрная линия — модельные значения, рассчитанные по формуле (3) при A = 1.1 и p = 0.32 (табл. 7). (б) кружки — фактические данные ВРП, чёрная линия — прямая наилучшего соответствия. Скорректированный коэффициент детерминации Ra ² = 0.92.

Республика Коми. ПФ (2) при C = СОФ для Республики Коми имеет Ra2 = 0.47 (табл. 8), то есть модель объясняет 47% разброса исходных данных и исключается из анализа. ПФ (2)

при C = ИОК значима и объясняет 67% разброса исходных данных; вклад ИОК в производство ВРП p = 29%, а ЧЗ q = 100 — p = 71%. При этом значимой корреляции между ВРП и ЧЗ не наблюдается (ВРП-ЧЗ = -0.23, ВРП-ИОК = 0.87, ВРП-СОФ = 0.18, табл. 1), то есть оценка моделей вида Y = L^q и Y = C^p при С = СОФ лишена смысла. Оценка модели Y = C^p при С = ИОК показывает (табл. 8), что модель значима и объясняет 82% разброса исходных данных; при увеличении ИОК на 1% ожидаемый прирост ВРП составит 0.22%. Эта модель имеет минимальное значение критерия AICc и является наиболее предпочтительной для Республики Коми; соответствие этой модели исходным данным показано на рис. 9.

Таблица 8 Оценки параметров моделей для Республики Коми по данным за 2000–2021 гг. при использовании в качестве капитала (С) стоимости основных фондов (С = СОФ) и инвестиций в основной капитал

(С = ИОК) 8

Параметр	Оценка	σ	t -value	Pr (>| t |)	F	p -value	Ra 2	AICc
ПФ (2), С = СОФ					19.3	2.8E-04	0.47	-33.4
log( A )	0.15	0.03	5.31	3.3E-05
p	0.30	0.07	4.39	2.8E-04
ПФ (2), С = ИОК					44.0	1.9E-06	0.67	-44.2
log( A )	0.08	0.03	2.67	1.5E-02
p	0.29	0.04	6.63	1.9E-06
ПФ: Y = AC Лр, C = ИОК					97.6	3.9E-09	0.82	-74.7
log( A )	0.09	0.01	6.34	3.5E-06
p	0.22	0.02	9.88	3.9E-09

• ⁸ Обозначения столбцов даны в примечании к табл. 2. Жирным шрифтом выделены модели, которые имеют только значимые параметры и объясняют не менее 60% разброса исходных данных.

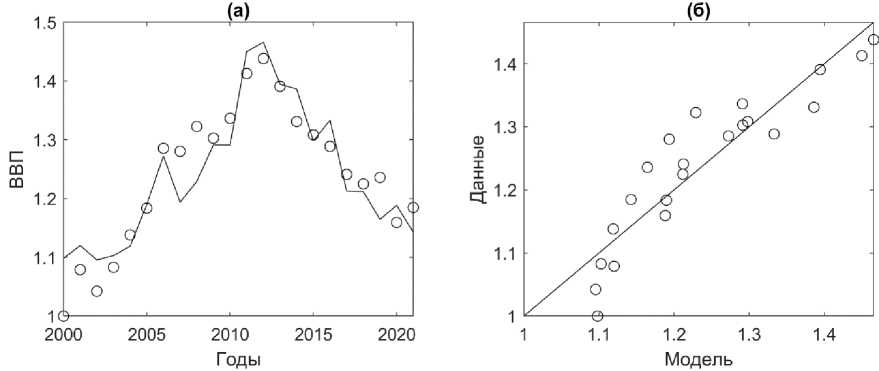
Рис. 9. Соответствие модели Y ~ C^p при C = ИОК исходным данным для Республики Коми за 2000–2021 гг. (a) кружки — фактические данные ВРП, чёрная линия — модельные значения, рассчитанные по формуле (3) при A = 1.09 и p = 0.22 (табл. 8). (б) кружки — фактические данные ВРП, чёрная линия — прямая наилучшего соответствия. Скорректированный коэффициент детерминации Ra ² = 0.82.

Для ряда регионов (Ямало-Ненецкий АО, Республика Саха Якутия) имеется значительная корреляция между ИОК и ЧЗ. Это позволяет оценить модель вида L ~ C ^p при C = ИОК и оценить влияние ИОК на ЧЗ для этих регионов. Расчёты показывают (табл. 9), что для обоих регионов модели являются статистически значимыми и объясняют не менее 72% разброса исходных данных. Для Ямало-Ненецкого АО при увеличении ИОК на 1% ожидаемый рост ЧЗ составляет 0.28%. Для Республики Саха (Якутия) при увеличении ИОК на 1% ожидаемый рост ЧЗ составляет 0.04%.

Таблица 9

Оценки параметров модели L ~ Cp для ряда регионов АЗРФ по данным за 2000–2021 гг. при использовании в качестве капитала инвестиций в основной капитал (С = ИОК) 9

Параметр	Оценка	σ	t -value	Pr (>| t |)	F	p -value	Ra 2
Ямало-Ненецкий АО, ПФ: L = C, C = ИОК					85.8	7.3E-09	0.72
p	0.28	0.01	19.41	6.8E-15
Респ. Саха (Якутия), ПФ: L = AC, C = ИОК					85.3	8.5E+01	0.80
log( A )	0.01	0.004	2.40	2.6E-02
p	0.04	0.004	9.23	1.2E-08

Заключение

Выяснение динамики ВРП, инвестиций в основной капитал, стоимости основных фондов, численности занятых регионов АЗРФ за 2000–2021 гг. показало, что имеются существенные различия в производстве ВРП этих субъектов. Анализ корреляций между ВРП и факторами производства (ВРП и инвестициями в основной капитал, ВРП и стоимостью основных фондов, ВРП и численностью занятых) подтвердил исходную гипотезу о разбалансированности взаимодействия основных факторов производства в ряде регионов АЗРФ.

Исходя из анализа корреляций регионы АЗРФ были разбиты на 3 группы: субъекты, в которых взаимное поведение основных факторов производства (труда и капитала) укладывается в общепринятые представления (РФ в целом, Ненецкий АО, Ямало-Ненецкий АО, Республика Саха (Якутия)); 2) субъекты, в которых взаимное поведение основных факторов производства не укладывается в классические представления: имеется достаточная по силе положительная связь (квадрат коэффициента корреляции не менее 0.6) лишь с одним из факторов производства (Архангельская область, Красноярский край, Республика Коми); 3) субъекты, для которых отсутствует достаточная по силе положительная связь (квадрат коэффициента корреляции менее 0.6) между ВРП и факторами производства (Мурманская область, Республика Карелия, Чукотский АО), что лишь частично согласуется с предшествующими результатами моделирования производственных процессов в регионах российского Севера и Арктики, указывая на их трансформацию [16, с. 38–39].

Для каждого региона группы 1 были построены как минимум 4 модели в виде ПФ (использовались показательная ПФ и ПФ Кобба-Дугласа). Лучшая модель выбиралась с помощью информационного критерия Акаике, скорректированного для малых выборок. Для каждого региона группы 2 оценены модели ПФ Кобба-Дугласа и однофакторные модели, в которые был включён фактор, имеющий положительную связь с ВРП. Построение моделей ПФ для регионов группы 3 невозможно.