Эксперимент натижаларини айта ишлашда сплайн функциялардан фойдаланиш

Маълумки, интерполяцион формулалардан турли хил амалий масалаларни ечишда кенг фойдаланиб келинмоқда. Шундай масалалардан бири эксперимент натижаларини қайта ишлаш масаласидир. Маълумки, эксперимент натижалари асосан жадвал кўринишда берилади. Бу эса ундан фойдаланиш имкониятларини чегаралаб қўяди. Масалан, эксперимент ўтказиш оралиқларида эксперимент натижаларини аниқлай олмаслик. Қандай усулда оралиқ эксперимент қийматларини тақрибий ҳисоблаш мумкин? Бу муоммани ҳал қилиш бир неча усуллар ёрдамида амалга ошириш мумкин. Шулардан бири сплайн функциялардан фойдаланишдир.

Фараз килайлик y=f(х ) функциянинг кийматлари n та нуктада берилган булсин, яъни yi=f(xi), i=1,..., n. Тугун нукталарни (n-1) та I_i=[x_i,x_i+1], i=1,..., n-1 кесмаларга ажратамиз.

^ар бир I i кесмага мос келувчи (n-1) та параболаларни g i ( x ) = a i 2 x ² + a i1 x + a i 0 , i=1,2,3,...,n-1

кўринишларда ифодалаймиз. Бу параболаларнинг бирлашмасидан иборат сплайн функцияни аниклаш учун 3(n-1) та a ij номаълум коэффициентлар зарур булади. 3(n-1) та номаълумни аниклаш учун шунча тенглама ҳосил қилиш лозим. Ҳар бир парабола учун интерполяция шартлари:

g i ^{( x}i ) = y_t , g i ^{( х} + 1 ) = У ш, =1,-, ^{n-1 (1)}

ёрдамида 2(n-1) та тенгламани косил киламиз.

(n-2) та нуктада параболалар кесишади, бу нукталарда сплайн функциянинг дифференциалланувчилигидан фойдаланиб, яна (n-2) та тенглама ҳосил қиламиз:

g i ^{( x} i + i ) = g ' + i ^{( x}i + i ) i= 1,..., ^n-2. ⁽²⁾

Натижада (3n-3) та номаълумли 2(n-1)+(n-2)=3n-4 тенгламага эга бўламиз. Сплайн функция ягона бўлиши учун яна битта шарт керак бўлади. Бу шарт сплайн функциянинг бирор тугун нуқтадаги оғишини бериш оркали аникланади, масалан g ‘ ( x₁ ) = d , бу ерда d- берилган катталик. Натижада, сплайн функцияни бир кийматли аникловчи (3n-3) та номаълумли (3n-3) та чизикли тенгламалар системасига эга буламиз.

Дастлабки 2(n-1) та интерполяция шартларини каноатлантирувчи тенглама қуйидаги кўринишга эга:

2 a12 x + an xi + aw                              = y 1 an x 2 + aiix 2 + aio                                = y2 2 a 22 x 2 + a 21 x 2 + a 20                    = y 2 a 22 x 3 + a 21 x 3 + a 20                    = y3 2 an -1,2 xn-1 + an -1,1 xn -1 + an -1,0 = yn -1 2 an -1,2 xn + an -1,1 xn + an -1,0     = yn Агар gi(x) = 2a^2x + a^1 эканлигини ^исобга олсак, (2) тенглама 2 ai 2 xi+1 + ai1 = 2 ai+1,2 xi+1 + ai+1,1 ёки 2ai2xi+1 + ai1 - 2ai+1,2xi+1 - ai+1,1 = 0. кўринишга эга бўлади. Шу сабабли сплайн функция дифференциалланувчанлигини ифодаловчи тенгламалар системаси қуйидагича ифодаланади:

2 a 12 x 2 + a 11 - 2 a 22 x 2 - a 21                                 = 0 2 a22x з + a 21 - 2 a 32 x 3 - a 3j               = 0 . 2 a n - 2,2 x n - 1 + a n - 2,1 - 2 a n - 1,2 x n - 1 - a n - 1,1 = 0 2 a 12 x 1 + a11                                             = d

Умумий ҳолда сплайн функция коэффициентларини аниқловчи

чизиқли

алгебраик  тенгламалар  системаси,  матрица  кўринишда

қуйидагича ифодаланади:

x 1²

x 2²

x ₁

x ₂

2 x ₂ x ₃ ²

x ₂  1

x ₃  1

.

.

.

2 x 2 1

—

2 x ₂

2 x ₃

— 1

1   0

2 x n — 1	x n — 1
2 xn	xn

^{— 2 x} 3 ^{— 1}

...

2 x n — 1   1 0

—

2 x ₁  1

² x n — 1

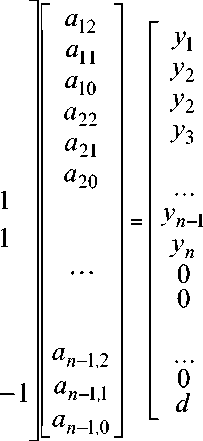
Матрицанинг бўш қолдирилган элементлари 0 га тенг. Бу системани ечиб (3n-3) та a^ номаълум коэффициентлар ани^лаймиз ва ^ар бир Ii=[xi,xi+1] кесмага мос келувчи gi (x ) = ai 2 x 2 + ai1 x + ai 0 , i=1,2,3,...,n-1

сплайн функциясига эга бўламиз.

Юқоридаги кубик сплайн функция қуриш алгоритми учун ABC Pasсal тизимида дастурий таъминот яратилган. Бу дастур ёрдамида қуйида берилган

x 12 16 20 24 28 32 y 11 15 13 12 14 15 тажриба натижалари қайта ишланиб, х нинг бир неча оралиқ қийматлари учун y нинг қийматлари аниқланган:

x	14	15,7	22	26,3	29
y	13,35	14,88	12,07	12,90	14,71

Хулоса сифатида шуни айтишимиз мумкинкин: жадвалдан кўриниб турибдики, тажриба натижаларини квадратик сплайн функцияларидан фойдаланиб қайта ишлаш усули юқори аниқликга эга; юқорида келтирилган тажриба натижаларини қайта ишлаш усулини кўп факторли тажриба натижаларига ҳам қўллаш мумкин. Шунингдек, қайта ишлаш натижаларининг аниқлигини ошириш учун юқори даражали, масалан кубик сплайн функциялардан ҳам фойдаланиш мумкин.

ФОЙДАЛАНИЛГАН АДАБИЁТЛАР РУЙХАТИ

• 1.    Yusupov, M., Tazhibayeva, R., Ziyaeva, S., Kubyashev K. (2021). Numerical modeling of the salt-transfer problem in soils. E3S Web of Conferences, 264, 01005.

• 2.    Рахманкулова, Б. О., Юсупов, М., Мирзаев, С. С. (2021). Numerical simulation of vehicle dynamics problems. Международный научный журнал «Научные горизонты», 2(42), 111-120.

• 3.    Юсупов, М., Мирзаев, С., Рахманкулова, Б. Международный

• 4.    Mirzaev S.S., Kholmatova I., Shadmanova G., Yusupov M. and Kubyashev K. Numerical modeling of two-dimensional two-phase filtration under frontal drive. Construction Mechanics, Hydraulics and Water Resources Engineering (CONMECHYDRO - 2020). Tashkent Institute of Irrigation and Agricultural Mechanization Engineers. 23-25 April, (2020).

• 5.    Yusupov, M., Akhmedov, B. A., & Karpova, O. V. (2020). Numerical simulation of nonlinear vibrations of discrete mass with harmonic force perturbation. Acta of Turin Polytechnic University in Tashkent, 10 (4), 71-75.

научный журнал «Научные горизонты», 2(42), 75-81.

"Экономика и социум" №11(90) 2021