Экспериментальная проверка алгоритма определения точки кюри электрода термопары по результатам измерения термоэдс

Введение. Постановка задачи1

Для оценки собственного состояния в средствах измерения температуры могут использоваться вещества с фазовыми переходами. Наибольшую распространённость на сегодня получили техниче- ские решения на основе точек плавления – разновидность фазовых переходов2 1-го рода [1]. Но уже проведены успешные опыты контроля показаний термопары по положению точек Кюри для фазовых переходов 2-го рода [2].

Эталонные вещества для калибровки термометров на основе фазовых переходов 2-го рода, по сравнению с аналогичными эталонными веществами на основе точек плавления обладают важным преимуществом – они находятся в твердом состоянии при всех рабочих температурах термометра. Коэффициент диффузии вещества в твёрдой фазе по сравнению с коэффициентом диффузии в жидкой фазе меньше на несколько порядков, поэтому эффекты загрязнения эталонного вещества оказывают гораздо меньшее влияние на температуру фазового перехода. Важным преимуществом такого технического решения является его технологичность, в том числе при реализации в одном измерительном устройстве нескольких точек фазового перехода, используемых затем для полной самостоятельной перекалибровки датчика температуры в процессе эксплуатации. Отметим, что при фазовых переходах 2-го рода не происходит выделения и поглощения энергии, а потому не изменяется температурная инерция сенсора.

В работе [2] была показана принципиальная возможность создания сенсоров с оценкой собственного состояния в процессе работы на основе термопары, но точные значения температуры Кюри полученных сплавов не были известны заранее. Поэтому оценить погрешность измерения термопарой точки Кюри по результатам работы [2] не представлялось возможным. Целью данной работы является уточненная оценка погрешности измерения температуры Кюри на основе термоЭДС термопары, одним из электродов которой является никель высокой чистоты – металл с заранее точно известной точкой Кюри, а вторым электродом является неферромагнитная платина – инертный металл, относительно которого принято измерять термоЭДС остальных металлов.

Физическая модель

Фазовый перехода 2-го рода протекает в широкой области изменения температуры, но заканчивается при строго определённой критической температуре Т с переходом в разупорядоченное состояние атомов сплава или магнитных моментов. При критической температуре происходит лишь изменение симметрии кристаллической решётки, сопровождаемое скачком производных от основных термодинамических характеристик: теплоёмкости, сопротивления, термоЭДС и др. К фазовым превращениям 2-го рода относятся переходы: парамагнетик – ферромагнетик, парамагнетик – антиферромагнетик, диэлектрик – сегнетоэлектрик, сопровождающиеся появлением самопроизвольной поляризации вещества, порядок – беспорядок в расположении атомов в решётке сплавов, а также переход от нормальной проводимости к сверхпроводимости. Известно, что наклон кривых температурной зависимости сопротивления и тер-моЭДС при Т _с изменяется так, что производные d p/ dT и dS/dT обнаруживают лямбда-пик при

Тс, то есть вблизи Тс температурное изменение этих величин можно представить одним и тем же законом [3]:

1 d p Р с dT

a T-T a^ Тс

-a

A

- 1 + B ,

где А , В и a - константы,

T _с – критическая темпе-

ратура. Поскольку a > 0, то из (1) следует, что при Т ^ Тс производные dp/dT и dS/dT стремятся к бесконечности (пик). Но так как измерения проводятся через конечный интервал по температуре, то реально при T = Tc должен наблюдаться макси- мум. Следует иметь в виду, что если Sa есть абсолютная дифференциальная термоЭДС электрода А, а Sb – электрода В, то измеряемая (интегральная) термоЭДС Е пары А–В при данной температуре Т:

T

E = J ( S a - S b ) dT .                          (2)

Примем, что металл А – ферромагнитный никель, а В – неферромагнитный металл, например, платина. Тогда продифференцировав выражение (2), найдём величину абсолютной дифференциальной термоЭДС никеля:

dE

S Ni =     ⁺ S Pt .

dT

Данные об абсолютной дифференциальной термоЭДС платины для многих температур приведены в монографии [4]. Аппроксимация численных значений полиномом третьей степени приводит к выражению:

S _Pt = ^ A i t , мкВ/К,                      (4)

i = 0

где А 0 = 2,39763;           А 1 = –2,894000∙10^–2;

А 2 = 1,105310∙10^–5;     А 3 = –2,513250∙10^–9.

Эксперимент

Для эксперимента была изготовлена никельплатиновая термопара, использовался никель чистоты 99,999 %. «Горячий» конец термопары вместе с эталонным термометром помещали в прецизионный термостат, «холодные» концы термопары подвергали термостабилизации в водно-ледяном термостате. ТермоЭДС термопары и термосопротивление эталонного термометра измерялись с помощью прецизионного преобразователя сигналов термосопротивлений и термопар. В эксперименте использовался неравномерный шаг задаваемой температуры, уменьшающийся в точке Кюри до 0,5 К. Результаты измерений приведены в виде графиков на рис. 1.

Обработка результатов эксперимента

Переводя измеренную температуру в Кельвины, как это принято в физике, проведем численное дифференцирование термоЭДС по температуре, а на основе формулы (3) рассчитаем абсолютную

Я .В. Кузнецов а, К.А. Уманец, М.Д.Белоусов, В.В. Дьячук , Д.А. Мирзаев, А.Л. Шестаков

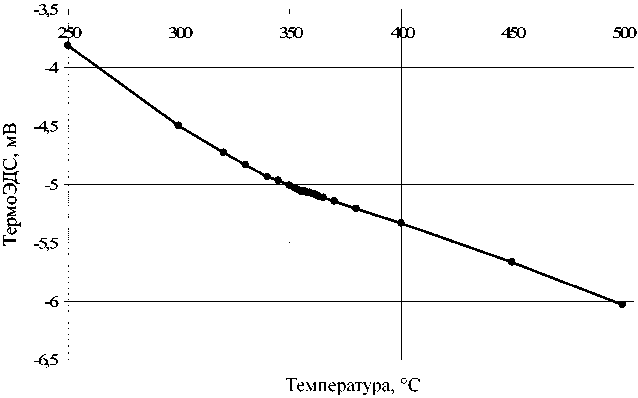
Рис. 1. Измеренная термоЭДС никель-платиновой термопары

дифференциальную термоЭДС никеля, учитывая, что абсолютная дифференциальная термоЭДС платины в [4] приведена в мкВ/К. Для повышения точности численного дифференцирования в качестве абсциссы использовали среднее значение температур соседних точек. Результаты приведены в виде графиков на рис. 2. Справочное значение точки Кюри никеля составляет 627,4 К [5].

Температура главного максимума составляет 629,68 К, а погрешность определения точки Кюри составляет соответственно 2,28 К.

На графике вблизи точки излома отчётливо наблюдается главный максимум, а также несколько локальных экстремумов. Эти экстремумы не могут быть объяснены наличием в измерительном тракте шумов, либо каких-нибудь других воздействий на измерительную аппаратуру. Природа данных экстремумов, по мнению авторов статьи, в следующем: поскольку в точке Кюри производная термоЭДС от температуры имеет точку разрыва, то при уменьшении шага дифференцирования численные расчеты решение становится нестабильными. Данная гипотеза подтверждается тем, что при достаточном увеличении шага численного дифференцирования указанные экстремумы полностью пропадают, однако при этом точность вычисления точки Кюри становится недостаточной. Данные локальные экстремумы численного дифференцирования, по мнению авторов работы, напротив, заключают в себе информацию о положении точки Кюри и должны использоваться в алгоритме её нахождения.

Для более точного нахождения точки Кюри производится второе численное дифференцирование данных графика на рис. 2. Его результаты приведены на рис. 3.

Для повышения точности численного дифференцирования в качестве аргумента полученной зависимости также используем средние значения

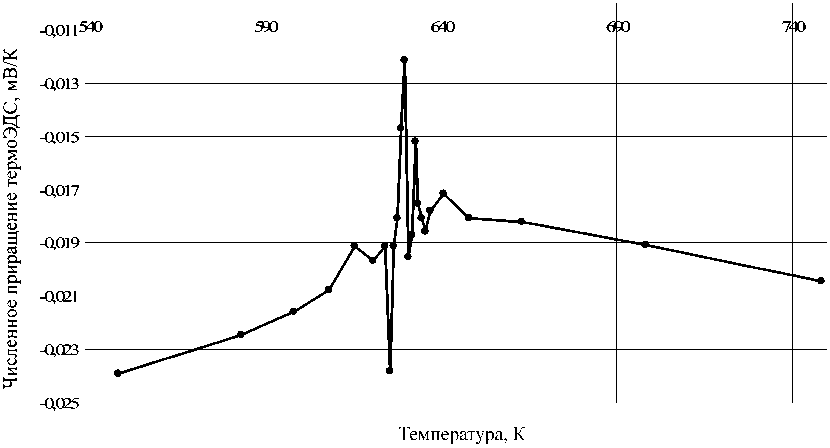
Рис. 2. Собственная термоЭДС никеля, полученная численным дифференцированием

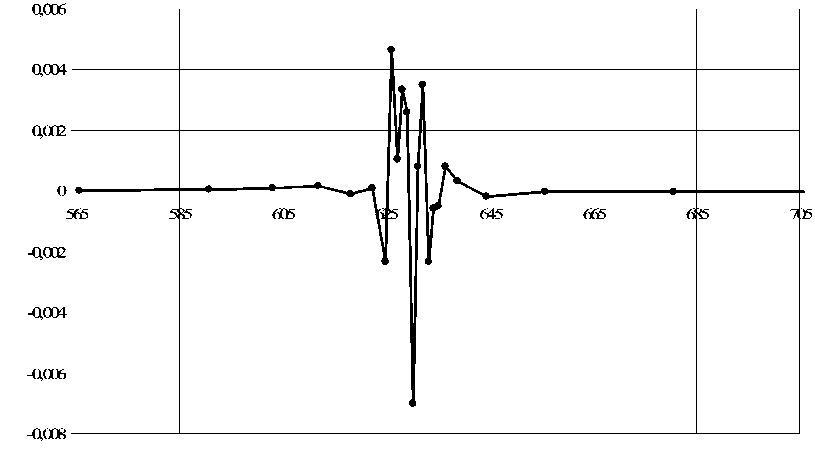
Рис. 3. Производная собственной термоЭДС никеля, полученная повторным численным дифференцированием

аргументов, по которым производилось дифференцирование.

Очевидно, что точка Кюри находится в области возмущений графика на рис. 3. Среднее значение температур максимума и минимума графика даёт значение 355,03 К, а погрешность определения точки Кюри составляет соответственно 0,78 К. Среднее значение крайних экстремумов, величина которых превышает 25 % от наибольшего экстремума, составляет 355,41 К, а погрешность определения точки Кюри составляет соответственно 1,17 К.

Порядок полученных погрешностей определения точки Кюри соответствует погрешностям термопар промышленного применения при исследуемых температурах [6].

Заключение

В результате данного исследования подтверждена работоспособность алгоритмов для оценки собственного состояния термометров на основе термопар с фазовым переходом 2-го рода.

Приведенное исследование показывает, что метод термоЭДС позволяет зафиксировать температуру фазового перехода 2-го рода. Оцененные погрешности метода составляют от 0,7 до 2,2 К и соизмеримы с погрешностями термопар, наиболее распространённых в промышленных измерениях при данных температурах.

Однако, вследствие существования лямбда-пика термоЭДС, для дальнейшего уменьшения погрешности, требуется специальные методы обработки экспериментальных данных, развитие которых, с точки зрения авторов, является дальнейшей задачей исследования.