Экспериментально-расчётное обоснование геометрических параметров резания корнеплодов

Введение. Процесс экстракции сахаров из корнеплодов [12] в значительной степени зависит от геометрических размеров формируемой стружки [10, 11]. Если получаемая толщина больше рекомендуемых размеров, то результативность операции экстракции снижается из-за сокращения объёма сырья, участвующего в диффузии. В противном случае, при меньшей толщине стружки, при экстракции происходит большее насыщение диффузионного сока несахарами, механическими загрязнениями остатков резания, что снижает качество получаемого продукта и ставит задачи дополнительной очистки в процессе производства. Это сопряжено с большей нагрузкой на технологию, персонал, окружающую среду [7, 8]. Дополнительным недостатком здесь является сложность в технической реализации малых значений толщины. Обоснование размеров свеклосахарной стружки в процессе производства сахара [9] из корнеплодов лежит в плоскости как теоретического исследования, так и экспериментальной оценки. Важным во всех случаях выступает поддержка элементами математического моделирования.

Основная часть. При современных технологиях получения сахара из свёклы, значительная её часть расходуется нерационально, так как продукт из сырья экстрагируется неполностью [1]. Для повышения выработки целесообразно провести исследование с применением математического моделирования.

Казалось бы, чем меньше толщина стружки, тем большее количество содержащегося в ней сахара диффундирует, что обеспечивает эффективность процесса. Однако, вследствие использования повышенных температур в технологии сахароотдачи, помимо большего количества мезги (мелких частиц корнеплодов), возникает другая весомая проблема – эффект скручивания свекловичной стружки меньшей толщины. При этом площадь поверхности контакта стружки с экстрагирующим агентом значительно снижается, что приводит к уменьшению выработки (экстракции) сахара.

Возникает задача оценки степени уменьшения площади стружки малой толщины при эффекте скручивания. Впоследствии эти величины становятся исходными данными для моделирования в системе «резание – экстрагирование» в технологии получения сахара.

Объектом экспериментально-расчётного проектирования [5] является плод сахарной свёклы среднего размера. Для формирования математической модели, объект условно признаётся шарообразным, характеризуемым усреднённым значением диаметра. При этом шар рассекается на части параллельными сечениями с заданным постоянным шагом i .

Для определения площади контакта стружки с экстрагирующим агентом (в эксперименте – с водой), принимаем расчётную геометрическую модель корнеплода (рисунок). Используя классическую теорему о хордах, имеем:

AE ■ EB = CE ■ ED .

В таком случае сечение CD удаляется от центра к периферии окружности диаметром D через определённый шаг i . Таким образом, формула приводится к следующему виду:

CE ²

f D 2

V

—

22 in

л

где n – число выполненных шагов сечения от центра окружности к периферии.

Исходя из такой формулы, площадь круга, получаемого в результате сечения, определяется следующим образом:

5 = _K. CE ² =п

f ^{D Т} T^— "

V n .

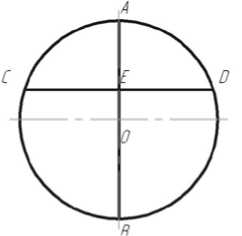
Рисунок 1 - Расчётная геометрическая модель корнеплода

В этом случае, при суммировании по полученной формуле, будет учтена только диаметральная половина окружности. Для определения всей площади поверхности контакта необходимо учесть дополнительное условие: так как стружка обладает двумя

поверхностями контакта, получаемая зависимость приводится к виду

N

5 E = S n = 0

f n2 ⁴"“

V

— i ² n ²   +-n D ²,

JJ 2

где N – число шагов от центра к краю окружности,

N = D — 1.

2 i

Средняя величина площади в таком случае может быть рассчитана по формуле:

5^ = .

ср 2 • ( 2 N + 1 )

Из выше изложенного следует, что максимальная площадь поверхности контакта стружки с экстрагирующим агентом получится при минимальном шаге нарезки i . В данной ситуации вероятен эффект скручивания стружки в трубочку, что изменяет в меньшую сторону площадь поверхности контакта.

Для оценки эффекта сворачиваемости осуществлен расчёт площади стружки, свернувшейся в трубку в результате термального воздействия при экстрагировании. Для упрощения такой задачи предложена модель, где площадь круга заменена площадью квадрата равной площади. При этом сторона такого квадрата равна

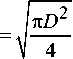
Экспериментируя со сворачиванием моделей в трубочку, принимаем условие, что каждый оборот будет иметь свою длину окружности. При известном диаметре получаемого внутреннего отверстия d формулы длин окружности имеют следующий вид:

Cо = nd; C = nd + n2 i; C2 = n d + 2n2 i, и т.д., что позволяет сделать вывод о закономерности увеличения длин окружностей в зависимости от шага

C n = n ( d + 2 iz ) , где z – число оборотов.

Таким образом, сумма всех длин будет находиться по формуле: z

C _E = X [n ( d + 2 ik ) ]• k = 0

На основе эксперимента определяем число слоев z , минимально превышающее сторону квадрата a .

В качестве программы математического моделирования использованы средства математического пакета MathCad. Подбирается первое (наибольшее) значение, при котором сумма длин получается немного больше, чем определённая величина стороны квадратаa . При подстановке в расчётную формулу осуществляется проверка по выражению Ce > a . Истинное значение выражения позволяет снизить число оборотов скручивания n на единицу, ложное – фиксирует величину n в имеющемся значении. В случае, если выражение Ce < a верно, остаётся часть, образующая незаконченный (по объему) цилиндр. Если получаемая длина окружности в его основании становится равной a - Ce , то часть незаконченного цилиндра становится равна q =     a - Ce     ,

¹ п ( d + ( z + 1 ) - 2 i )

а оставшаяся часть незаконченного цилиндра будет равна

_ i a — C ^      .

q 2       n ( d + ( z + 1 ) - 2 i )

Таким образом, площадь незаконченного цилиндра можно вычислить по формуле:

51 _ qina [ d + 2 i (z +1)] ■

Площадь законченного цилиндра будет равна

5 2 _ q 2 П a ( d + 2 iz ) ■

Внутри цилиндра имеется полость, площадь поверхности которой определяется выражением:

5 о _ n da ■

Таким образом, общая площадь поверхности стружки, скрученной в цилиндр в результате термического воздействия, вычисляется по формуле:

5 _ 5 ₀ + 5 1 + 5 2 .

На основе результатов, полученных после проведённого эксперимента [17], установлено отношение площади плоской стружки корнеплода для сахароотдачи к площади её свернувшейся формы в интервале от 2 до 5. Для плодов большего размера, такая величина может достигать интервалаот 11 до 13.

Выводы: В результате экспериментально-расчётного моделирования подтверждена технологическая нецелесообразность использования стружки меньшей толщины. Большая эффективность диффузии при меньшей толщине стружки в результате полного процесса диффузии не учитывает явление скручивания, которое увеличивает технологическую толщину за счёт слойности. Таким образом, для определения оптимальной величины толщины стружки следует руководствоваться данными о скручивании, что позволит учесть специфику процесса.

При этом рекомендованная в литературных источниках толщина стружки в 1 мм, трудно реализуема на производстве [13]. Это связано с тем, что интенсивное механическое воздействие приводит к образованию большего количества мезги, большему вымыванию трудно удаляемых далее несахаров, а также продиктовано сложностью производственной реализации малых значений толщин получаемой стружки [18]. На сегодняшний момент используются устройства центробежного, барабанного и дискового принципа действия, реализующих большее значение толщины, например, 4 - 7 мм [19].

Ранее авторским коллективом проводилось экспериментальное исследование [3, 4, 6, 14-16], которое на практике подтвердило выше представленные утверждения.

Полученные экспериментально-расчётные обоснования и конкретные рекомендации позволяют при моделировании и проектировании процесса диффузии сахаров из корнеплодов обеспечить оптимальные технологические параметры процесса резания, эффективно обеспечивающего формирования заданного оптимального значения толщины стружки.