Экспериментальное исследование деформаций бедренной кости с установленным эндопротезом тазобедренного сустава

Большое количество работ посвящено экспериментальному исследованию влияния конструкции эндопротеза на напряженно-деформированное состояние бедренной кости. Проведенные экспериментальные исследования выявили особенности влияния конструкции эндопротеза на перераспределение внешней нагрузки в бедренной кости. Недостатком экспериментальных методов исследования являются технические ограничения, не позволяющие моделировать сложные условия нагружения системы кость–имплантат, отражающие физиологическую активность человека. Кроме того, для описания процессов, протекающих в костной ткани, необходима регистрация напряжений внутри кортикального слоя бедренной кости, которая также трудно осуществима при экспериментальном подходе. Поэтому все большую популярность завоевывают методы математического моделирования механического поведения

задняя сторона А – А внутренняя сторона

наружная сторона передняя сторона

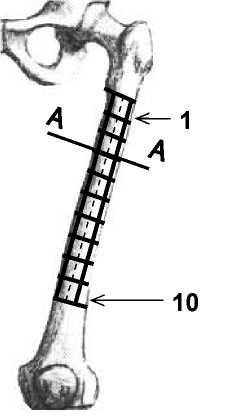
Рис. 1. Участки измерений продольных перемещений системы кость–эндопротез. При этом полученные экспериментальные данные используются для верификации параметров и оценки адекватности математических моделей.

В настоящей работе описано экспериментальное исследование, проведенное для проверки адекватности математического моделирования механического поведения конечно-элементной модели бедренной кости с установленным эндопротезом тазобедренного сустава. Сравнение результатов численного и натурного экспериментов показало соответствие экспериментальных данных численному решению.

Экспериментальное исследование продольных деформаций кортикального слоя бедренной кости

Для проверки адекватности математического моделирования механического поведения конечно-элементной модели бедренной кости с установленным эндопротезом тазобедренного сустава в лаборатории физико-механических свойств материалов Института механики сплошных сред УрО РАН при участии сотрудников кафедры травматологии, ортопедии и военно-полевой хирургии Пермской государственной медицинской академии проведено экспериментальное исследование полей продольных деформаций наружного слоя бедренной кости при воздействии на нее вертикальной нагрузки в 3000 Н, близкой по величине и направлению к физиологическим нагрузкам, действующим на тазобедренный сустав.

Бедренная кость при помощи специально изготовленных подкладок была закреплена в анатомическом положении на испытательном приборе 1925ПА-10М и нагружена со скоростью 5 мм/мин. Наружная поверхность бедренной кости была размечена в продольном направлении на 10 одинаковых участков (рис. 1).

Продольные поверхностные перемещения регистрировались тензодатчиком наружного крепления с базой 25 мм. Измерения проводились с передней, задней, внутренней и наружной сторон каждого участка. В результате проведенного эксперимента были получены данные о перемещениях в 40 участках бедренной кости. Далее в бедренную кость был установлен эндопротез модели "Феникс" и проведена повторная серия испытаний (рис. 2). По измеренным продольным перемещениям было

а

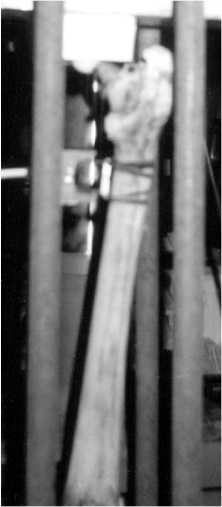
б

Рис. 2. Расположение «здоровой» бедренной кости (а) и эндопротезированного бедра (б) на испытательном приборе 1925ПА-10М определено поле продольных деформаций "здоровой" и протезированной бедренной кости (рис. 3,4). Анализ результатов эксперимента показал линейное поведение системы кость-имплантат при внешних нагрузках до 3000 Н.

Для математического моделирования механического поведения бедренной кости с установленным эндопротезом была построена пространственно неоднородная анизотропная линейно-упругая модель системы кость-имплантат.

Модель системы кость–имплантат

Система бедро-эндопротез представляет собой неоднородное анизотропное линейно-упругое тело сложной геометрической формы (рис. 5). Неоднородность вызвана различием механических свойств эндопротеза, кортикальной и губчатой костных тканей. Эндопротез и губчатая кость являются изотропными материалами, кортикальная кость - ортотропным материалом. Фиксация имплантата в костном ложе обеспечивается прорастанием костной ткани в пористое покрытие поверхности эндопротеза.

Механическое поведение системы, занимающей область V в R ³ с границей S , описывается следующими уравнениями линейной теории упругости:

V• о = 0, x е V,(1)

£ = _(Vu + (Vu)T), x е V ,(2)

о = E(x) • •£, x е V ,(3)

u = 0, x е Su,(4)

n • о = 0, x е S\(( Sp n Sb) и Su и S,),(5)

n • о -1 = 0, x е St,(6)

где V = V U S , S = S u U S t , о - тензор напряжений; в - тензор упругих деформаций; E ( x ) - тензор упругих свойств.

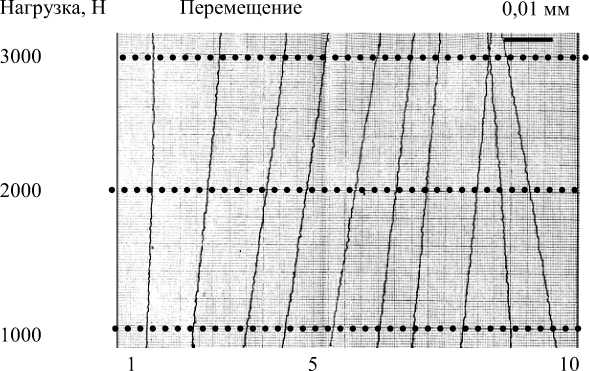
Номер участка

Рис. 3. Графики продольных перемещений, зарегистрированных в 1 – 10 участках переднего края «здоровой» бедренной кости

Нагрузка, Н

Номер участка

Рис. 4. Графики продольных перемещений, зарегистрированных в 1 – 10 участках переднего края протезированной бедренной кости

S t

S b

u

S p

Рис. 5. Расчетная модель системы кость–имплантат: Sb – полная поверхность кости, включая поверхность мозгового канала, Sp – поверхность имплантата, Sb ∩ Sp – поверхность контакта кости с имплантатом, St – поверхности нагружения, Su – поверхность поперечного расчленения бедра

Исследуемая область имеет сложную геометрическую форму и неоднородное распределение анизотропных механических свойств, поэтому для определения пространственного напряженно-деформированного состояния системы кость-имплантат применим метод конечных элементов.

При построении конечно-элементной модели бедренной кости с установленным эндопротезом используем ортогональную декартову систему координат. Ось Y направим вдоль продольной оси бедра, ось Z перпендикулярна фронтальной плоскости и образует с осями X , Y правостороннюю ортогональную систему координат.

Математическая модель механического поведения системы бедренная кость – эндопротез

Для определения пространственной геометрии исследуемой области использованы: бедренная кость трупа 50-летнего мужчины и эндопротез модели "Феникс" (рис. 6).

Для построения пространственной конечно-элементной модели (рис. 7) использованы тетрагональные элементы с линейной аппроксимацией перемещений.

Экспериментальному исследованию механических свойств твердых биологических тканей посвящены многочисленные исследования [1-5, 7]. При расчетах используем данные об анизотропных механических свойствах кортикальной кости, полученные в экспериментальной работе [5] (табл. 1). Спонигиозную кость будем моделировать однородным материалом с изотропными механическими свойствами, взятыми из работы [7] (табл. 2). В табл. 3 приведены необходимые для расчетов значения материальных констант имплантата.

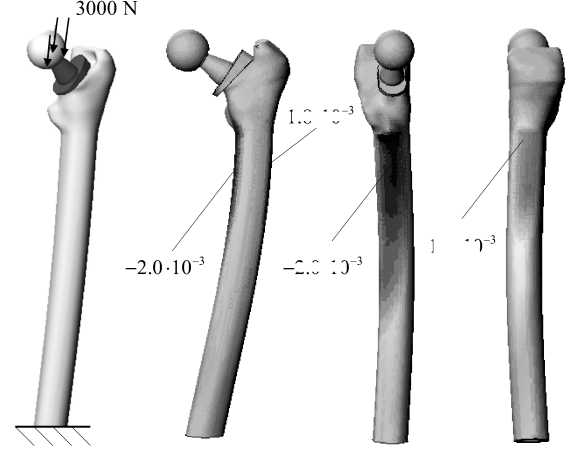
С помощью построенной пространственной конечно-элементной модели системы бедро-эндопротез были рассчитаны поля продольных деформаций бедренной кости при следующих граничных условиях: нижний край кости консольно закреплен; головка протеза нагружена вертикальной нагрузкой 3000 Н (рис. 8).

Сравнительный анализ экспериментальных данных и результатов численного решения

Величины поверхностных продольных деформаций на внутреннем и наружном крае бедренной кости, зарегистрированных в эксперименте и рассчитанных при помощи численной модели, отображены на рис. 9, 10.

Как видно из рис. 9, 10, результаты проведенного экспериментального исследования хорошо согласуются с имеющимися литературными данными. Наблюдаемые на рис. 9 различия в величине продольных деформаций вызваны тем, что при проведении испытаний авторы работы [6] консольно закрепляли нижнюю часть бедренной кости, а в нашем исследовании бедренная кость фиксировалась на испытательной машине при помощи специально подготовленной подкладки. Некоторые количественные отличия экспериментальных данных от результатов численного решения (рис. 10) обусловлены некоторой неопределенностью данных о механических свойствах исследованной бедренной кости и использованием при расчетах значений из литературных источников.

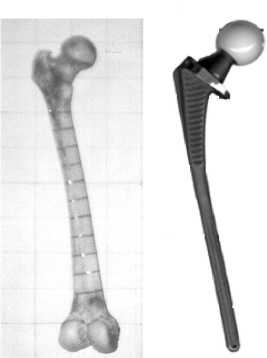
а

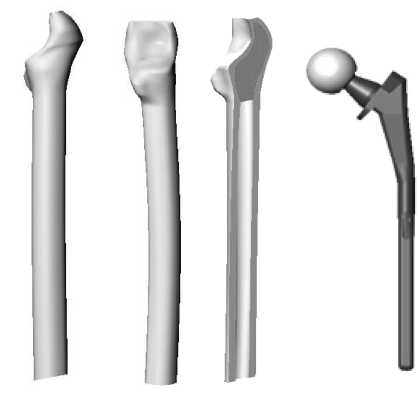
Рис. 6. Пространственная модель бедренной кости и эндопротеза "Феникс": а – физический объект, б – конечно-элементная модель

Таблица 1

Механические свойства кортикальной костной ткани
	Независимые постоянные	Значение
	E X	8,70 ГПа
	E Y	17,10 ГПа
	E Z	8,70 ГПа
	G XY	4,15 ГПа
	G XZ	4,50 ГПа
	G YZ	4,15 ГПа
	ν XY	0,25
	ν XZ	0,05
	ν YZ	0,50

Механические свойства губчатой костной ткани

Модуль упругости, E , ГПа	Коэффициент поперечной деформации, ν
2,50	0,32

Таблица 2

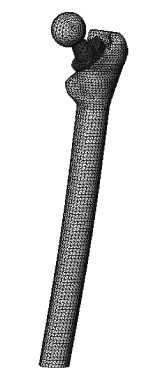
Рис. 7. Пространственная конечно-элементная модель системы бедро–эндопротез

1.8 ⋅ 10

-

2.0 ⋅ 10

а                б

1.8 ⋅ 10

• 2.0 ⋅ 10 ^{- 3}

• 1.8 ⋅ 10 ^{- 3}

• 1.6 ⋅ 10 ^{- 3}

• 1.4 ⋅ 10 ^{- 3}

• 1.2 ⋅ 10 ^{- 3}

• 1 .0 ⋅ 10 ^{- 3}

0.8 ⋅ 10 ^{- 3} 0.6 ⋅ 10 ^{- 3} 0.4 ⋅ 10 ^{- 3} 0.2 ⋅ 10 ^{- 3}

• - 0.2 ⋅ 10 ^{- 3}

• - 0.4 ⋅ 10 ^{- 3}

• - 0.6 ⋅ 10 ^{- 3}

• - 0.8 ⋅ 10 ^{- 3}

• - 1.0 ⋅ 10 ^{- 3}

• - 1.2 ⋅ 10 ^{- 3}

• - 1.4 ⋅ 10 ^{- 3}

• - 1.6 ⋅ 10 ^{- 3}

• - 1.8 ⋅ 10 ^{- 3}

• - 2.0 ⋅ 10 ^{- 3}

в                г

Рис. 8. Граничные условия (а) и результаты расчета продольных деформаций: б – деформация бедра во фронтальной плоскости, в – продольные деформации на внутреннем крае, г – продольные деформации на наружном крае

Таблица 3

"Феникс"

Механические свойства элементов

Модуль упругости, E , ГПа	Коэффициент поперечной деформации, ν
210,00	0,32

3000 H

по данным [6] эксперимент

ε , %

Рис. 9. Продольные деформации на наружном и внутреннем крае «здоровой» бедренной кости, полученные в эксперименте, в сравнении с данными других авторов

3000 H

по данным [6]

эксперимент численное решение

I ε , %

Рис. 10. Продольные деформации на наружном и внутреннем крае протезированной бедренной кости, полученные в эксперименте, в сравнении с численными расчетами и данными других авторов

Заключение

Проведенное экспериментальное исследование показало, что система уравнений 1–6 адекватно описывает механическое поведение системы бедро–имплантат. Использование метода конечных элементов для расчета напряженно- деформированного состояния данной системы позволяет количественно рассчитать поля деформаций, подтвержденные в эксперименте.