Экспериментальное исследование модели фандрайзинга с фиксированной величиной рекомендованного пожертвования

Исторически широко известны проекты на основе краудфандинга – осуществляемые за счёт жертвователей – доноров, которые добровольно способствуют реализации некоторого проекта своими финансовыми пожертвованиями, бесплатной работой и другими ресурсами. С развитием электронных платёжных систем получили широкое распространение проекты, финансируемые через Интернет, появились специализированные платформы – kickstarter.com, planeta.ru, indiegogo.com и ряд других, но поскольку платформы берут существенную комиссию за свои услуги, то многие проекты осуществляют сбор средств на своих собственных сайтах. Одной из разновидностей краудфандинга является фандрайзинга – предполагается что донор не получит от реализации проекта какого-либо специального вознаграждения или это вознаграждение чисто символическое (бесплатно раздаваемая открытка, благодарственный e-mail и т.д.). Феномену фандрайзинга посвящено значительное число публикаций, но они в основном изучают общественные и медийные аспекты, эконометрическому анализу посвящено мало публикаций, можно отметить работу1, в которой приведены сводные данные по ряду крупных фандрайзинговых компаний.

Многие, возможно даже почти все, краудфандинговые проекты помимо собственно вариантов поддержки проекта с реальным вознаграждением, предлагают варианты с символическим, например проект на Kickstarter по созданию светящихся растений2 предлагал следующие варианты финансирования – 5$ (стикер на телефон); 25$ (футболка); 40$ (семена светящихся растений); 65$ (ваза из переработанной электрической лампочки и семена светящегося растения); 65$ (чашка для выращивания и семена светящегося растения); 80$ (ваза другого типа и семена светящегося растения); 90$ (руководство по выращиванию и семена светящегося растения); 120$ (семена светящегося растения в первой поставке); 150$ (выращенный экземпляр светящегося растения в первой поставке); 250$ (набор для выращивания светящегося растения); 500$ (возможность закодировать сообщение длиной до 140 символов в коде ДНК, которая будет выслана донору и семена светящегося растения); 5000$ (однодневный мастер-класс разработчиков к выездом к донору); 10 000$ (сообщение длиной до 30 символов будет закодировано в коде ДНК светящегося растения). Легко видеть, что самые дешёвые и дорогие позиции связаны скорее с моральным удовлетворением, а не с материальной выгодой от реализации проекта. Проект собрал на Kickstarter 484013 $ от 8433 доноров, стал одним из самых знаменитых, сильно повлиял на общественное сознание и на нормативную базу – в частности Kickstarter после финансового успеха проекта запретил краудфандинговые кампании, связанные с генной модификацией. К сожалению, реализация проекта скорее закончилась неудачей – растения светились очень тускло и разработчикам не удалось выполнить требования законодательства США, поэтому он был свёрнут, а накопленные опыт и технологии попытались вложить в проект создания ароматного мха, вызвавшего неоднозначную реакцию аудитории. Для исследователя подобные компании представляют интерес тем, что указывают, сколько тех или иных лотов было реально приобретено. К сожалению, несколько осложняют исследование лоты, где все экземпляры выбраны, но всё-таки обычно число «символических» лотов, не влекущих материального вознаграждения, организаторами не ограничено.

Настоящая работа посвящена разработке структуры модели, с помощью которой в перспективе можно будет оптимизировать процесс фандрайзинга – увеличить скорость сбора пожертвований. Полезным инструментом для анализа особенностей сбора пожертвований является твиттер-аккаунт «Мундеп-деньги», данные с которого позволили уточнить модель, разработанную на основании опыта финансирования проекта «Памяти МИХМа» и проведённые в социальных сетях Одноклассники и Facebook опросы.

Структура модели фандрайзинга

Сложилось три основных подхода к финансированию проектов:

– донор может пожертвовать произвольную сумму (в рамках возможностей платёжной системы, например в диапазоне 1 – 15 000 рублей при использовании Яндекс-денег), рекомендуемый размер пожертвования не указывается, см. например3;

– указывается один или несколько рекомендуемых размеров пожертвований с комментариями (100 рублей – «Спасибо! », 500 рублей – «Большое спасибо», либо указанием – на сколько часов продлится деятельность проекта за счёт этого пожертвования и т.д.). Как правило, в этом случае также даётся возможность пожертвовать произвольную сумму;

• -    донору предлагается подписаться на ежемесячный платёж (обычно с банковской карты). Этот способ удобен для планирования финансового состояния проекта, в реальности составляет существенную часть финансирования ряда проектов, но в данной работе не рассматривается.

Сформулируем принятые при разработке модели допущения4:

• -    успешная реализация проекта не даёт каких-либо преимуществ донорам, т.е. он может пользоваться (или не пользоваться) результатами наравне с лицами не принимавшими участия в проекте;

• -    участие в проекте не приносит проблем донору;

• -    исключаем из рассмотрения доноров с очень большими финансовыми возможностями (как правило есть ограничения на максимальный размер платежа, и с такими донорами ними проводятся переговоры и поддержка идёт отдельно, не общим порядком);

• -    принимаем что минимально возможное пожертвование (в 2017 году - обычно 100 рублей) является незначительной суммой для практически всех потенциальных доноров;

• -    считаем незначительной комиссию платёжных систем или платформ-посредников (в некоторых случаях комиссия может быть очень значительной, но учёт влияния комиссий требует отдельного рассмотрения). Например, если комиссия 3% берётся с получателя пожертвования и донор пожертвовал 100 рублей, то получатель получил 97 рублей. В этом случае принимаем, что пожертвование составило 100 рублей. Если комиссия берётся с донора (т.е. получателю отправляется 100 рублей, а с донора списывается 103 рубля), то также принимаем что пожертвование составило 100 рублей;

• -    принимаем, что за время сбора средств не происходит заметных изменений в финансовом состоянии доноров и не происходит вызванного инфляцией обесценивания собранных средств. Поскольку большинство фандрайзинговых компаний длятся несколько дней или недель (см. [1, 2]) то это допущение выглядит довольно реалистично, но для случаев когда донор жертвует средства в виде ежемесячного и ежегодного платежа (а такой вариант очень привлекателен для долгосрочных проектов), необходим учёт инфляции;

• -    предполагается что потенциальные доноры обладают соизмеримыми финансовыми возможностями, принадлежат одному сообществу - если пожертвования собираются в разных странах или в сообществах с заметно различными уровнями доходов, то модель имеет смысл разбить на несколько, с учётом этих фактов;

• -    пожертвования «некруглого» размера не учитываются в рамках текущей работы, т.к. они явно являются сочетанием желания помочь проекту и одновременно - обнулить счёт списания. Учёт таких платежей может быть введён в модель дополнительно, но как правило они очень

малы, т.к. являются остатком на счету, который не получается потратить обычным образом.

Хотя наиболее часто встречается ситуация, когда проект рекомендует фиксированную сумму пожертвования, с возможностью ввода донором произвольной суммы в некоторых пределах, ограниченных платёжной системой или законодательством (последнее ограничение, например, критично при финансировании предвыборных компаний кандидатов в муниципальные депутаты) и в настоящей работе возможность ввода произвольной величины пожертвования не рассматривается.

Допустим, что посетитель сайта проекта готов стать донором – пожертвовать x рублей (мера удовлетворения донора проектом, мера желания ему помочь, текущих финансовых возможностей донора). По общему мнению⁵ доля доноров составляет не более 1 – 3% от числа заинтересованных в успешном завершении проекта, поднимаясь примерно до 10% только в исключительных случаях.

Будем предполагать, что величина x >  0 является случайной, её значения для каждого донора независимы, а x подчиняется некоторому стационарному закону, например – экспоненциальному:

f ( x ) = e - ‘ x ’ , (1) где f ( x ) - доля доноров, готовых пожертвовать x рублей или меньшую сумму, т.е. небольшие суммы готовы пожертвовать почти все доноры, а крупные – почти никто;

• - Л_х - параметр модели, фиксированный для конкретного проекта и

  совокупности доноров.

  
  
  

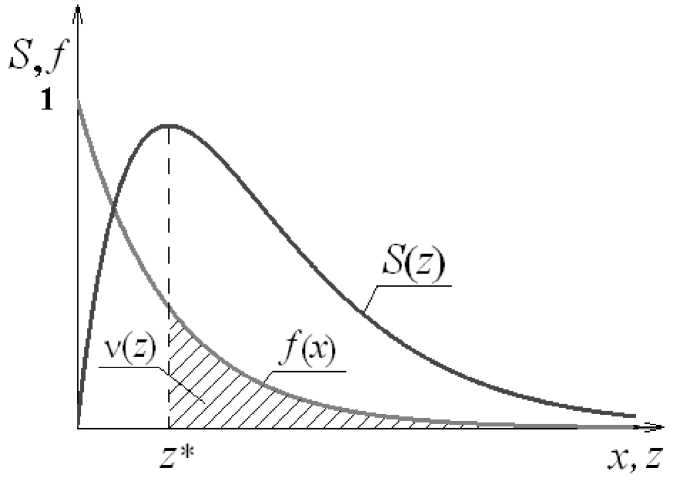
  Рис. 1. Зависимость доли готовых к пожертвованию доноров f ( x ) и общей суммы сборов S ( z ) от величины рекомендованного пожертвования

  
  

Обозначим сумму рекомендованного пожертвования z. Доля доноров, готовых пожертвовать не менее z рублей равна v(z) = j f (x)dx = e-z4 4 , а общий объём полученных средств составит S(z) = Nv(z)z = Nze"z4 /4 , где N - общее количество потенциальных доноров. Найдём оптимальное значение z * , обеспечивающее максимум

S (z):

dS^ = 0 ^ e- ^ x z *( 1 - z* 4 ) = 0 ^ z* = —.

dz              ^X      x’              4

На рис. 1 проиллюстрированы вышеприведённые рассуждения.

Оценку параметра 4 можно найти из статистики проекта: например предлагая потенциальным донорам две рекомендованные суммы

(обозначим их как zx и z2) или показывая потенциальному донору случайным образом одно из двух значений фиксированное число раз. Обозначим число совершённых пожертвований на сумму zx и z2 как пх и n2, соответственно. С учётом ранее полученного выражения для v(z), найдём

_{х =} M n l/ n J x      z 2 ^- z i

Получив параметр модели 4 можно скорректировать величину рекомендуемого пожертвования и добиться большей величины сборов.

Экспериментальное исследование фандрайзинга

Эксперимент 1. Эксперимент, проведённый с помощью проекта «Памяти МИХМа»6. На главной странице портала была установлена форма для сбора пожертвований от Яндекс-денег (ЯД), полученные средства зачислялись на ЯД-кошелёк, с которого списываются средства на хостинг проекта. Также доноры направляются на страницу, где они могут видеть текущее состояние баланса ЯД. Набору лично знакомых людей администраторы проекта высылали сообщение с предложением поддержать проект и ссылкой на страницу портала, где предварительно устанавливалась величина рекомендованного пожертвования 100, 500 или 1000 рублей. Эксперимент проводился более года (с осени 2015 по весну 2017), было получено, что вероятность пополнения счёта портала на 100, 500 и на 1000 рублей - практически одинаковая. Многие адресаты перезванивали, писали ответные письма, убеждались, что письмо прислали не мошенники и, примерно, в 5 процентах случаев от общего числа адресатов рассылки поддерживали проект, причём практически всегда - на рекомендованную сумму. Таким образом, было показано, что для случая с персональным обращением к донору предложенная модель не применима.

Эксперимент 2. В социальной сети Одноклассники было создано сообщество, куда вступило более 2000 человек, заинтересованных в развитии проекта «Памяти МИХМа». На портале проекта была создана страница для сбора пожертвований доноров, пришедших со страницы упомянутого сообщества, таким образом, были получены реальные данные, по которым с использованием формулы (2) была найдена величина оптимального рекомендуемого пожертвования – 400 рублей. После публикации страницы сбора пожертвований с величиной рекомендованного пожертвования 400 рублей, вместо ожидаемого роста было получено резкое снижение пожертвований, они практически прекратились, более того, установив величину рекомендуемого пожертвования 200 рублей также были получены сборы значительно меньшие, чем когда рекомендуемое пожертвование было равно 500 рублей. Для прояснения этого обстоятельства в упомянутом сообществе был создан анонимный опрос, в котором участникам предлагалось ответить, какой размер пожертвования для них является наиболее предпочтительным. Результаты опроса представлены на рис. 2.

Табл. Результаты опроса в социальной среде Одноклассники

Величина пожертвования	100	150	200	250	300	400	500	700	900	1000	1100	1500	2000
Число проголосовавших	5	0	5	0	6	0	5	0	0	4	0	0	0

Всего опрос открыли более 1700 уникальных пользователей, потенциальные доноры ни одного раза не выбрали величины 150; 250; 400; 700; 1100; 1500; 2000 рублей, что согласуется с данными реальных платежей. Таким образом, исключим из набора данных значения, которые не были выбраны и построим на основе полученных экспериментальных данных экспериментальную и модельную

Экспериментальные данных хорошо согласуются с моделью (1).

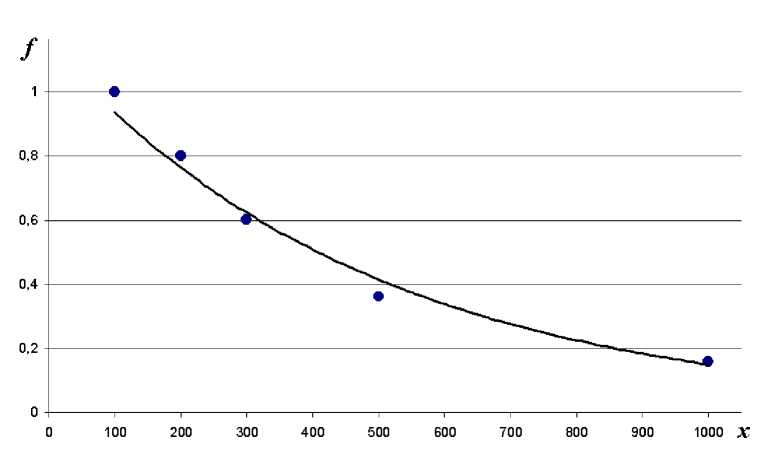
Рис. 2. Сравнение экспериментальных значений f ( x ) и построенных по уравнению (1)

Эксперимент 3. В социальной сети Facebook в сообществе «Проблемы образования и науки», в котором на момент опроса было около 2000 членов был размещён опрос, аналогичный опросу эксперимента 2. В опросе приняло участие 43 человека, были получены результаты аналогичные эксперименту 2, за исключением того, что пользователи выбрали значения из набора (100; 500; 1000; 1500), т.е. довольно «популярные» у пользователей Одноклассников значения 200 и 300 рублей совершенно не интересны для пользователей Facebook.

По результатам экспериментов 2 и 3 можно сделать вывод, что для конкретной аудитории по предварительным опытам возможно определить ряд «допустимых» значений и параметры модели, после чего выбрать из «допустимых» значений величину z , обеспечивающих максимум функции S ( z ) .

Эксперимент 4. В ходе эксперимента проанализированы сообщения о поступивших пожертвованиях в твиттер-аккаунте «Мундеп-деньги»7 в период с 8 сентября по 17 октября 2017 года. В качестве рекомендуемых величин пожертвования предлагались 1000; 1500; 3000 рублей. При анализе оставлены только «круглые» значения пожертвований и только в рублях – данные по другим валютам малочисленны. Всего таких платежей оказалось 79. На рис. 4 представлены данные, обработанные аналогично рис. 3.

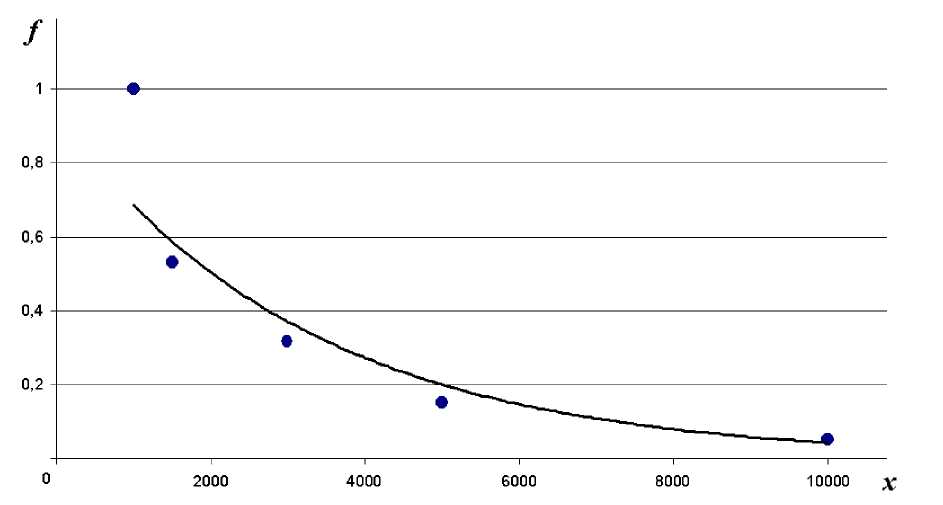
Рис. 3. Сравнение экспериментальных значений f ( x ) и построенных по уравнению (1) для реальных сборов

Из рис. 4 видно, что несмотря на то, что среди предложенных рекомендованных значений не было 5000 и 10000 – заметное количество доноров всё-таки сделали такое пожертвование. Модель (1) хорошо описывает данные на рис. 3, особенно если исключить первую точку, x =1000. По предыдущим экспериментам также видно, что величина х= 1000 является «предпочтительным» значением для многих пользователей, что необходимо учитывать при определении параметров модели.

Следует принимать во внимание, что использование только трёх рекомендуемых значений вынуждает использовать для анализа «самостоятельно» введённые донорами значения 5000 и 10000, что требует усложнения модели и учёта влияния «трудоёмкости» самостоятельного введения значения пожертвования.

Выводы

По результатам анализа ряда фандрайзинговых проектов становится очевидным, что в большинстве случаев жертвуется именно одна из рекомендованных сумм, т.е. трудозатраты донора по определению для себя допустимого пожертвования и вводу его в строку ввода довольно значительны – люди предпочитают просто нажать кнопку с одной из уже обозначенных величин. Более того, некоторые значения – например 200 рублей, 900 рублей – являются, видимо, менее предпочтительными, чем 250 и 1000 рублей. Скорее всего, это связано с психологическими эффектами.

При сборе статистики следует принимать во внимание, что аудитория доноров, пришедшая с разных информационных площадок существенно различается по своим финансовым характеристикам и техническим навыкам. На основе собственных наблюдений автор полагает, что аудитория социальной сети Facebook существенно легче отзывается призывы к поддержке проекта и испытывает значительно меньше технических трудностей при проведении платежа, чем аудитория социальной сети Одноклассники, хотя с другой стороны – аудитория Одноклассников намного более стабильна в своей поддержке проекта.

Возможные направление развития работы

Полученная модель может быть модифицирована:

• 1.    Возможно усовершенствование сбора и анализа статистики проекта, например путём организации рандомизированного показа рекомендуемого пожертвования;

• 2.    Эксперимент 4 показывает, что для ряда проектов необходимо введение учёта возможности ввода произвольной суммы пожертвования;

• 3.    Возможно, необходим учёт пожертвований сумм, существенно больших, чем рекомендуемая;

• 4.    Если проект существует долгое время (более нескольких месяцев), то значения коэффициентов модели могут измениться, соответственно возникает задача определения периода пересчета величины рекомендуемого пожертвования по текущим данным.