Экспериментальное исследование расхода масла через подшипник турбокомпрессора при различных параметрах процесса смазки и условиях эксплуатации

В сегменте дизельных двигателей для грузовых автомобилей и тяжелой техники в последнее время основное внимание уделяется надлежащей смазке, использование которой обеспечивает долговечность ДВС, экономию топлива и снижение вредного экологического воздействия [1–3]. Однако стремление к увеличению производительности, повышению качества производственных процессов заставляет непрерывно увеличивать мощность используемых ДВС. Эффективным способом прибавки мощности выступает оснащение ДВС турбонаддувом [4–6]. Турбонаддув обеспечивает без значительных конструктивных доработок прибавку мощности на 20…50 % [7– 9]. Трендом сегодняшнего машиностроения выступает даунсайсинг [10–13]. Даунсайсингом называется направление конструктивного совершенствования современной автотракторной техники, обеспечивающее существенную прибавку мощности при сохранении габаритно-массовых размеров силовых агрегатов. Однако помимо значительной прибавки мощности автотракторная техника, оборудованная турбонаддувом, становится очень уязвимой к качеству используемых смазочных материалов, срокам технического обслуживания, соблюдению тепловых и нагрузочных режимов и т. д. [14–16]. Перечисленные недостатки заставляют машиностроительные предприятия разрабатывать большое количество систем, узлов и механизмов, устраняющих данные недостатки. Среди них можно выделить: турботаймер, конструктивную доработку подшипников и масляных каналов, саморегулирующиеся элементы и узлы турбокомпрессора, антипомпажные клапаны, электронные системы управления процессами работы турбокомпрессора и его смазки, новые узлы системы смазки турбонаддува, системы масляного, воздушного и жидкостного охлаждения турбонаддува, механизмы преодоления турбоямы [17–19].

Актуальна проблема поддержания необходимого расхода масла через подшипниковый узел при обеспечении заданного температурного режима [20–22]. Решить эту задачу можно посредством технологических, конструктивных, эксплуатационных мероприятий. На наш взгляд, значительными преимуществами обладает конструктивное мероприятие, заключающееся в установке в систему смазки автономной смазочной системы с регулируемым электрическим приводом [23– 25]. Автономный привод масляной системы имеет ряд существенных преимуществ: использование прокачки масла при запуске ДВС, установка любой необходимой подачи масла независимо от режима работы ДВС, обеспечение заданного теплового режима подшипника ТКР, обеспечение высокой надежности подшипника ТКР в эксплуатации. Однако для всестороннего изучения возможностей применения автономной системы смазки требуется проведение комплексного исследования по обоснованию допустимых и достаточных границ эффективности ее работы. С учетом сказанного целью исследования выступает теоретический и экспериментальный анализ расхода масла через подшипник турбокомпрессора (ТКР) при варьировании величины входного давления и оборотов вала ротора турбокомпрессора при постоянной температуре входного масла 50 °С.

Материалы и методы

Основой теоретических исследований является анализ применимости различных уравнений по определению расхода масла через подшипники ТКР [26–28]. За основу анализа возьмем формулу контроля коэффициента чувствительности:

К =А П , A U

где А П - интервал диапазона изменения расхода масла через подшипник ТКР, л/с (м ³ /с); A U -интервал диапазона изменения структурного параметра (давление масла на входе в подшипник ТКР ( P вх ), МПа и частота вращения вала ротора ТКР (n, мин^–1).

Анализ моделей, рабочих выражений и формул для расчета расхода масла через подшипники вала ротора ТКР позволил выявить значительное их число. Рассмотрим основные из них:

Широко известная формула Рейнольдса:

Q = п • D • h • n • -^Р- • | ^{A P}- | ,                                                              (2)

2 • р ^ р • L )

где Q – объемный расход масла через подшипник, м³/с; D – диаметр вала ротора ТКР, м; h – ра- диальный зазор в подшипнике ТКР, м; n - частота вращения вала ротора ТКР, об/с; р - вязкость масла, м2/с; р - плотность масла, кг/м3; AP - разность величин давлений перед входом в подшипник ТКР, Па; L – длина подшипника ТКР, м.

Вычислим чувствительность параметра Q от n :

dQ , Р ( A P Л — = п • D • h • —•!I dn 2 • р ^ р • L )

Определим чувствительность параметра Q от P :

dQ           L

— = п • D • h • n---

dP

2 • Р

Формула Рейнольдса – одна из самых простых формул в области определения расхода масла, но ее применение ограничено низкой точностью. Она не учитывает влияние эксцентриситета и радиуса кривизны [29].

Формула Лэмба:

Q = п • D • h • n • ^P -⁽ 1 + 6 • - H^ P | ,                                                  (5)

p L     h ) L p • L J где - - эксцентриситет вала ротора ТКР, м.

Определим выражение для расчета чувствительности параметра Q от n :

dQ      p 7      (л   - Л ( A P

— = п • D • h • — • I 1 + 6 • — I • II.(6)

dn            p L      h ) ^ p • L )

Выразим показатель чувствительности параметра Q от P :

dQ = п • D • h • n • L -(1 + 6 •- \(7)

dP           p L

Формула Лэмба учитывает значение эксцентриситета, однако применяется при расчетах для подшипников с малым эксцентриситетом ( ε / h < 0,1).

Формула Петрусевича:

p ,    P (7  - £Л (7 h Л ( ^ P Л

Q = п • D • h • n I l + 6 •—I'I l +--I-I------I .                                                          (8)

P L       h ) L 3 • R ) L P • L )

Определим чувствительность расхода масла Q от частоты вращения вала ротора турбоком- прессора n:

dQ      p 7 P (-   -           h ( A P Л

— = п • D • h • — • I 1 + 6 •- I-I 1 +-----I-I----- I .

dn           p L      h )L 3 • R ) L P • L )

Вычислим чувствительность параметра Q от P :

dQ     p 7     P (7   - ^£ Л (, h Л

= п • D • h • n 1 + 6 •    •   1 + .

dP             p L      h )L 3 • R )

Формула Петрусевича гораздо более точна, чем формула Лэмба. Она учитывает влияние радиуса кривизны поверхности вала ( R ).

Формула Ляпунова:

(        £2 Л

Q = п • D • h • n • ^P '1 +12 • — • ----- .                                                      (11)

p l        h ² ) L p • l )

Определим чувствительность параметра Q от n :

dQ p 7 P

— = п • D • h • —• dn         p

£² Л

1 + 12 • — • h2 J

A P p • L

Выразим чувствительность параметра Q от P :

dQ = п • D • h • n • ^L • ⁽1 +12 • ^—— dP            p L       h ²

Формула Ляпунова имеет самую высокую точность из представленных выше, но сложная в применении. С применением прикладных программ расчетов рекомендуется к применению для получения достоверных результатов.

Формула Стерлинга:

(

Q = п • D • h • n11 + 3 •—I'  1 + p L      h) I

h ²

12 • D ²

A P p • L

Вычислим чувствительность параметра Q от n :

dQ = x-d • h • P .(1 + 3 • - )• dn          p L      h )

h ²

12 • D ²

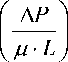
Определим чувствительность параметра Q от P :

dQ            L I     £i

— = n • D • h • n---1 1 + 3 ■— I •

dP

p

h

1 +------2

к 12 • D ²

Формула Стерлинга имеет существенное сходство с формулой Ляпунова, но менее точная.

Формула Гюгонио:

Q = n • D • h • n • — •11 + 6 •£ P к      h.

(

•  1 +

к

h ²

к

12 • D ² _J

(

•  1 +

к

£ h2 J

AP

— • L

Выразим чувствительность параметра Q от n :

dQ    — , P — = n • D • h • — • dn         p	(1 + 6• £ ] • к       h J	f,       h 2 1 + к   12 • D 2 j		I    /22 ^ 1 + — к    h 2 J	1 A P
			•		к — • L

Вычислим чувствительность параметра Q от P :

dQ               — I .£

— = n • D • h • n •   • 1 + 6 •• dP            p к

к

1 + h 2 к 12 • D2j

I

•  1 +

к

£

h 2 _J

Формула Гюгонио обладает самой высокой точностью, но ее применение значительно усложняется.

В качестве основных выводов следует отметить: формула Рейнольдса рекомендуется к использованию для расчета параметров процесса смазки подшипников ТКР с малым эксцентриситетом. В том случае, когда применяемые подшипники ТКР имеют малый и средний эксцентриситеты, рекомендуется использовать формулу Петрусевича. Формулы Ляпунова и Гюгонио могут быть применимы для расчета параметров процесса смазки для подшипников ТКР с любым эксцентриситетом.

Для возможности проведения экспериментальных исследований была спроектирована и разработана независимая (автономная) система смазки подшипников ТКР (рис. 1).

Независимая (автономная) система смазки ТКР (см. рис. 1) состоит из масляного бака, электродвигателя, масляного насоса, приводимого в движение электродвигателем, нагревательных тэнов, встроенных в масляный бак, соединительных масляных магистралей, измерительных датчиков и контрольных устройств. Независимая (автономная) система смазки ТКР представляет собой универсальную систему, которая может быть использована для полноценного питания всех элементов ДВС или только для смазки подшипников ТКР. Электродвигатель и частотный регулятор независимой (автономной) системы смазки ТКР могут работать от аккумулятора или электрической сети 220 Вольт в случае стационарного двигателя или генераторной установки.

В представленных исследованиях автономная система смазки подсоединялась только к магистрали питания турбокомпрессора. Все элементы автономной системы смазки компактно размещались под экспериментальным стендом (рис. 2).

Рис. 1. Независимая (автономная) система смазки

Fig. 1. Independent (autonomous) lubrication system

Рис. 2. Экспериментальный стенд

Fig. 2. Experimental stand

Независимая (автономная) система смазки ТКР со средствами измерения максимально приближена к контролируемому турбокомпрессору (см. рис. 2). Длины соединительных масляных магистралей выбраны с учетом минимизации пути масла и минимальной диссипации тепловой энергии до места входа масла в подшипник ТКР.

С целью контроля выбранных входных и выходных параметров в гидравлические соединения были подсоединены следующие датчики и устройства: расходомеры масла в подающей магистрали и стоке подшипника ТКР, датчик мгновенного давления, термопары для контроля мгновенных изменений температуры масла в подающей магистрали и на стоке подшипника ТКР (рис. 3).

Рис. 3. Используемые датчики для комплексного контроля рабочих параметров масла

Fig. 3. Sensors used for complex monitoring of oil operating parameters

Рис. 4. Датчик контроля частоты вращения вала ротора ТКР

Fig. 4. Turbocharger rotor shaft speed control sensor

В отдельные точки системы смазки ТКР подсоединены датчики (см. рис. 3). Их присоединение выполнено с учетом минимального воздействия на увеличение гидравлического объема и гидравлических сопротивлений.

Для фиксации значений частоты вращения вала ротора ТКР использовался датчик Д-01Н, работа которого основана на эффекте Холла (рис. 4).

Датчик контроля частоты вращения вала ротора ТКР (см. рис. 4) представляет собой магнитную систему со специальными мерками, встроенными во вращающиеся элементы турбокомпрессора. Контроль всех входных и выходных параметров производился с помощью цифрового осциллографа USB AutoScope 4. Обработка полученных осциллограмм входных и выходных параметров производится в приложении USB AutoScope 4.

Анализ и обработка статистических данных выполнены в программном приложении SigmaPlot с использованием стандартных встроенных функций данной программы.

Результаты и обсуждения

В результате проведения эксперимента получены данные, представленные в табл. 1.

Как видно из табл. 1, было реализовано 9 последовательных опытов, в которых на постоянном уровне поддерживалась температура масла на входе в подшипник ТКР ( T вх = const = 50 °С). В процессе экспериментальных исследований варьированию подвергались две входные величины: давление масла на входе в подшипник ТКР ( P_вх ) в пределах 0,1…0,4 МПа и частота вращения вала ротора ТКР ( n ) в пределах 25000…75000 мин^–1. В качестве выходных величин оценивались три характеристики: расход масла на сливе ТКР ( Q ), время наполнения мерной емкости объемом 1 литр ( t нап ) и температура масла на сливе из турбокомпрессора ( Т вых ). Применяя статистическое приложение SigmaPlot, получили трехмерный полигон данных (рис. 5).

Таблица 1

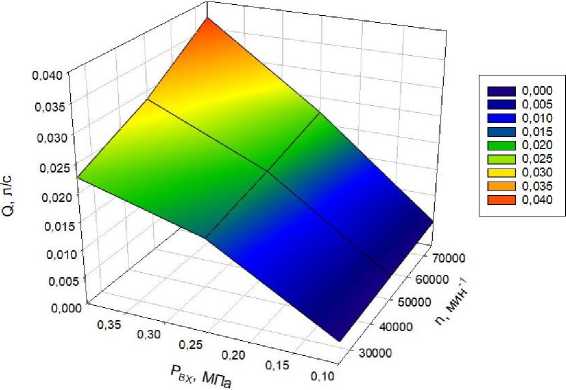
Результаты многофакторного эксперимента при T вх = 50 °С

Table 1

Results of a multifactorial experiment at T in = 50 °С

№	–1 n , мин	T вх , °С	P вх , МПа	tнап , с	T вых , °С	Q , л/с
1	25000	50	0,1	256	57	0,0039
2	50000	50	0,1	228	59	0,0044
3	75000	50	0,1	206	63	0,0049
4	25000	50	0,25	60	55	0,0167
5	50000	50	0,25	52	56	0,0192
6	75000	50	0,25	45	58	0,0222
7	25000	50	0,4	44	53	0,0227
8	50000	50	0,4	35	54	0,0286
9	75000	50	0,4	27	56	0,0370

Рис. 5. Экспериментальная взаимосвязь расхода масла через подшипник ТКР Q , л/с от величины оборотов вала ротора ТКР n , мин^–1 и величины входного давления масла перед подшипником ТКР P вх , МПа при постоянной температуре масла на входе в подшипник ТКР T вх = const = 50 °С

Fig. 5. Experimental relationship between oil flow through the turbocharger bearing Q , l/s, and the value of the turbocharger rotor shaft speed n, rpm, and the value of the inlet oil pressure in front of the turbocharger bearing P in , MPa at a constant oil temperature at the inlet to the turbocharger bearing T in = const = 50 °С

Анализ полигона данных на рис. 5 показывает, что зависимость выходного показателя Q , л/с, существенно падает с понижением P вх , МПа. Падение P вх при n = const сопровождается уменьшением расхода масла через подшипник ТКР. Причем в начале характеристика давления на входе в интервале 0,4…0,25 МПа идет более полого, с небольшим наклоном к оси, обозначающей изменение P вх . В интервале значения Pвх = 0,25…0,1 МПа наблюдается более резкое снижение Q , л/с, и при P вх = 0,1 МПа, значение Q достигает минимума – 0,004 л/с. Более динамичный спад характеристики расхода масла наблюдается при n = 75000 мин^–1 в пределах изменения P вх =0,4…0,1 МПа, по сравнению c условиями при n = 25000 мин^–1.

Из данных на рис. 5 видно, что при P вх = 0,1 МПа наблюдается минимальное изменение Q при увеличении величины оборотов вала ротора ТКР. При возрастании числа оборотов вала ротора ТКР с 25000 до 75000 мин^–1 величина параметра Q увеличилась на 0,0009 л/с.

В тот же момент при P вх = 0,4 МПа можно видеть более резкое изменение Q при одновременном изменении оборотов вала ротора ТКР с 25000 до 75000 мин^–1 (см. рис. 5). Увеличение Q составляет 0,0143 л/с, что является существенным, и объясняется данное увеличение активным увлечением масла в рабочий зазор подшипника. Увеличение частоты вала ротора на 50000 мин^–1 приводит к динамическому приросту расхода масла на величину Δ Q = 0,0143 л/с.

Для возможности определения уравнения регрессии было использовано приложение SigmaPlot с методикой аппроксимации экспериментальных данных 4 различными методами: модель плоскости, параболическая модель, функция Гаусса, кривая Лоренца. Результаты подбора уравнения регрессии и критерии правильности подбора модели представлены в табл. 2.

Таблица 2

Критерии выбора модели

Table 2

Model selection criteria

Вид уравнения	R	R 2	R2	SE
Модель плоскости	0,972	0,944	0,926	0,0031
Параболическая модель	0,978	0,956	0,913	0,0034
Функция Гаусса	0,997	0,994	0,989	0,0012
Кривая Лоренца	0,997	0,994	0,989	0,0012

Получены 4 уравнения, аппроксимирующие кривую, представленную на рис. 5: Q = -0,0101 +1,3876 • 10 ^{- 7} • n + 0,0835 • Р вх .

Q = -0,0136 + 5,7756 • 10 ^{- 8} • n + 0,1382 • P_m + 8,1 •Ю ^{- 13} • n ² - 0,1093 • Р 2_X . вх                                     вх

Q = 1,8828 • е

I n -1,0210 5 ⁰,51            «

I 3,36105 к

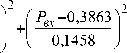
0, 4779

, I n -2,63 • 10 5 I Г  P^ - 0,3420Л

1 + ------—  • 1 + —------- к 6,87• 105  J к      0,0780 J

Анализ данных табл. 2 и уравнений (20)–(23) показывает, что наилучшую точность описания экспериментальных точек дают функция Гаусса и кривая Лоренца. Полученные уравнения регрессии можно использовать в эксплуатации для контроля расхода масла через подшипник ТКР при вариации параметров n и P вх .

На следующем этапе экспериментальной обработки данных необходимо оценить качествен- ную характеристику взаимосвязи выходных параметров с варьируемыми величинами входных факторов. Коэффициент чувствительности выражает величину приращения контролируемого параметра (оценочного параметра) с учетом варьирования структурного параметра (величины, которую напрямую можно оценить простыми методами контроля). В случае если контролируемый параметр окажется нечувствительным, принимается решение об исключении технического контроля ТКР по данному параметру.

Рассмотрим изменение величины чувствительности параметра расхода масла через подшипник ТКР от величины давления масла на входе в ТКР (табл. 3).

Таблица 3

Данные для оценки чувствительности параметра расхода масла

Table 3

Data for assessing the sensitivity of the oil consumption parameter

№	–1 n , мин	Т вх , °С	Р вх , МПа	tнап , с	T вых , °С	Q , л/с
1	25000	50	0,1	256	57	0,0039
2	25000	50	0,25	60	55	0,0167
3	25000	50	0,4	44	53	0,0227
4	50000	50	0,1	228	59	0,0044
5	50000	50	0,25	52	56	0,0192
6	50000	50	0,4	35	54	0,0286
7	75000	50	0,1	206	63	0,0049
8	75000	50	0,25	45	58	0,0222
9	75000	50	0,4	27	56	0,0370

На основании табл. 3 построим графическую зависимость расхода масла через подшипник ТКР от величины давления масла на входе в подшипник ТКР и трех фиксированных значений оборотов вала ротора ТКР (рис. 6).

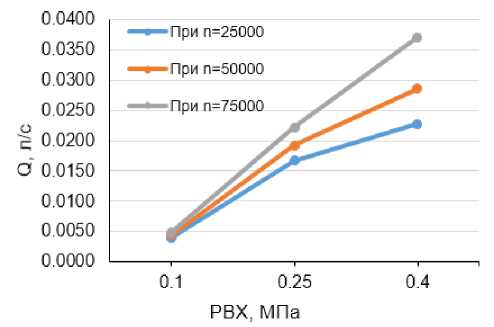
Рис. 6. Взаимосвязь расхода масла через подшипник ТКР (при Т вх = 50 °С) от величины давления масла на входе в подшипник ТКР и трех фиксированных значений оборотов вала ротора ТКР

Fig. 6. The relationship between oil flow through the turbocharger bearing (at Т in = 50 °С) and the oil pressure at the inlet to the turbocharger bearing and three fixed values of the turbocharger rotor shaft speed

Как видно из рис. 6, графическая зависимость расхода масла через подшипник ТКР показывает нелинейный рост в зависимости от изменения P вх .

Рассмотрим методический аппарат определения чувствительности. Основным критерием является коэффициент чувствительности. Но на начальном этапе его определения необходимо установить разность расходов масла через подшипник ТКР при изменении структурного параметра от максимальной до минимальной величины. Для чего воспользуемся формулами:

^{A 0} 25000 = 0 (25000)0,4 - 0 (25000)0,1 ^.

^{A 0} 50000 = 0 (50000)0,4 - 0 (50000)0,1 •

^{A 0} 75000 = ⁰ (75000)0,4 - ⁰ (75000)0,1 •

С ростом значения частоты вращения вала ротора ТКР, разность фиксируемых величин расходов масла на выходе ТКР возрастает. То есть это говорит об активном вовлечении масла в рабочий зазор подшипника ТКР и росте степени прокачиваемости. Увеличение расхода масла обеспечивает значительный положительный эффект, который заключается в лучшем отводе температуры из рабочего зазора проходящим маслом.

Для вычисления коэффициента чувствительности расхода используем формулы:

К ,. = рас 25

A ⁰ 25000 A P х

К рас 50

^{A 0} 50000

A P х

К = рас75

^A 0 75000 A P х

Коэффициент чувствительности существенно возрастает с приростом частоты вращения вала ротора ТКР, что говорит о высокой компенсаторной способности и возможности адаптации гид- равлических компонентов системы смазки.

Проведем графический анализ чувствительности расхода масла через подшипник ТКР. Для этого сгруппируем точечные данные для удобства вычислений (табл. 4).

Воспользовавшись результатами табл. 4, получили взаимосвязь (рис. 7).

Как видно из рис. 7, характеристики расхода масла через подшипник ТКР при малых значениях входного давления масла в подшипник ТКР обнаруживают линейный вид. При P вх = 0,4 МПа характеристика приобретает нелинейный вид и гораздо больший угол наклона к оси n .

Для расчета коэффициента чувствительности вычислим на начальном этапе разность расходов в пределах от максимального до минимального значений n:

^{A 0} 0,1 = ⁰ (0,1)75000 - ⁰ (0,1)25000 •                                                                       ⁽³⁰⁾

^{A 0} 0,25 = ⁰ (0,25)75000    ⁰ (0,25)25000 ^.

^{A 0} 0,4 = ⁰ (0,4)75000    ⁰ (0,4)25000 •

Таблица 4

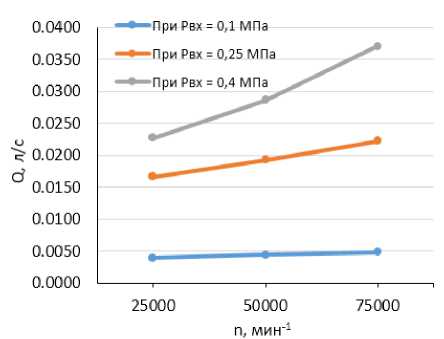
Рис. 7. Взаимосвязь величины расхода масла через подшипник ТКР (при Т вх = const = 50 °С) от изменения оборотов вала ротора ТКР при трех фиксированных значениях давления масла на входе в подшипник ТКР

Сгруппированные точечные данные для определения чувствительности расхода масла

Table 4

Grouped point data for determining oil consumption sensitivity

№	–1 n , мин	Т °C вх ,	Р вх , МПа	tнап , с	Т °C вых ,	Q , л/с
1	25000	50	0,1	256	57	0,0039
2	50000	50	0,1	228	59	0,0044
3	75000	50	0,1	206	63	0,0049
4	25000	50	0,25	60	55	0,0167
5	50000	50	0,25	52	56	0,0192
6	75000	50	0,25	45	58	0,0222
7	25000	50	0,4	44	53	0,0227
8	50000	50	0,4	35	54	0,0286
9	75000	50	0,4	27	56	0,0370

Fig. 7. The relationship between the value of oil flow through the turbocharger bearing (at Т in = const= 50 °С) and the change in the speed of the turbocharger rotor shaft at three fixed values of oil pressure at the inlet to the turbocharger bearing

С повышением частоты вращения вала ротора ТКР разность расходов масла на выходе ТКР возрастает. Это говорит об активном вовлечении масла в рабочий зазор подшипника ТКР и росте степени прокачиваемости. Увеличение расхода масла обеспечивает значительный положительный эффект, который заключается в лучшем отводе температуры из рабочего зазора проходящим маслом.

Для вычисления коэффициента чувствительности расхода используем формулы:

к    - ^ 0 1

К рас 25      _А     ^.

Л n

_ ^Л Q 0,25 К рас 50 = д

,    _ Л 0 0,4

^{рас 75}     Л n  ■

Анализ проведенных расчетов указывает на активную динамику прироста коэффициента чувствительности с возрастанием параметра Р_вх . Рост Р_вх происходит по нелинейному закону. В процессе возрастания давления масла обнаруживается действие динамического подпора, который стремится поджать вал к подшипнику. В случае, когда вал неподвижен, обнаруживается его блокировка подпором масла от вращения отработавшими газами. Поэтому давление масла независимой системой смазки необходимо повышать постепенно. Кроме того, действует важный механизм – чем существеннее подпор масла на входе в подшипник, тем выше расход масла через него

(тем более при вращении вала ротора ТКР). Установленные граничные условия необходимо использовать в практике эксплуатации современных ТКР с автономным питанием.

Выводы

Уровень развития современной техники показывает на непрерывное стремление к увеличению выходной мощности ДВС при сохранении габаритно-массовых параметров неизменными. Это направление получило название даунсайсинг. Результатом развития данного направления стало активное форсирование основной массы автотракторных ДВС. Однако недостатком применения турбонаддува является значительное повышение чувствительности новых систем к качеству топлива, масла, расходных материалов, срокам и качеству обслуживания. Одновременно значительно возросли удельные нагрузки на системы ДВС, и, как следствие, произошло снижение надежности и ресурса автотракторных средств. Для повышения надежности ТКР была разработана автономная система смазки с возможностью регулирования параметров входного давления и температуры масла, обеспечиваемой встроенными тэнами. Кроме того, обеспечивалось изменение скоростного режима турбокомпрессора независимо от гидравлических параметров потока масла. В процессе экспериментальной работы осуществлялась фиксация расхода масла через подшипник ТКР с учетом изменения входных параметров, процесс изменения которых осуществлялся независимо друг от друга. Причем уже на этапе запуска ДВС можно обеспечивать максимальные значения входных параметров, гарантируя их независимое варьирование. Проведенные расчеты показали на непрерывный рост коэффициента чувствительности расхода масла от варьируемых входных величин. Это обеспечивает положительный тренд прироста расхода масла в любой момент работы ТКР, исключая граничное трение. Таким образом, представленные результаты могут быть использованы эксплуатирующими и конструкторскими организациями для повышения надежности использования автотракторных средств в сельском хозяйстве.