Экспериментальное исследование сплавов с памятью формы, применяющихся в медицине

Сплавы с памятью формы нашли применение во многих отраслях науки и техники, в частности в медицине. Известно множество примеров использования имплантатов и устройств из никелида титана в ортодонтии [1, 8, 11, 12, 16], челюстнолицевой хирургии [1, 9], сердечно-сосудистой хирургии [6, 22], хирургии и ортопедии [1, 6, 17, 23] и т.д.

Развитие современных технологий и методов математического моделирования (особенно в области определяющих соотношений для материалов с памятью формы) позволяет проводить биомеханический анализ данных медицинских приложений.

Однако для эффективного моделирования необходимо знать свойства конкретного материала, из которого изготовлено то или иное устройство и исследовать его механическое поведение. Обычно проводятся испытания на растяжение–сжатие [10, 24]. Установлено, что на параметры гистерезиса влияют температура испытания, скорость деформирования, предварительная термообработка образцов и химический состав.

В литературе доступны данные испытаний различных сплавов с памятью формы. В работе [18] приведены результаты циклического поведения сплава NiTi © Кучумов А.Г., Лохов В.А., Словиков С.В., Вильдеман В.Э., Штраубе Г.И., Суторихин Д.А., 2009 Кучумов Алексей Геннадьевич, аспирант кафедры теоретической механики, Пермь Лохов Валерий Александрович, к.ф.-м.н., доцент кафедры теоретической механики, Пермь Словиков Станислав Васильевич, к.т.н., ведущий инженер Центра эксперимент. механики, Пермь Вильдеман Валерий Эрвинович, д.ф.-м.н., профессор, директор Центра эксперимент. механики, Пермь Штраубе Галина Ивановна, д.м.н., профессор, заведующий кафедрой челюстно-лицевой хирургии, Пермь Суторихин Дмитрий Александрович, к.м.н., доцент кафедры челюстно-лицевой хирургии, Пермь

(Ni – 55,9% и Ti – 44,1%) при разных скоростях деформации и температурах. Было показано, что напряжение фазового перехода и величина энергии диссипации зависят от температуры отжига. Статья [24] посвящена испытаниям образцов (Ni – 50,9% и Ti – 49,1) с различной степенью пористости. Показано, что с увеличением пористости образца его прочность понижается. В работе также была представлена модель, описывающая поведение образцов, и приведены результаты сравнения экспериментальных и теоретических данных. Результаты испытаний на кручение образцов при сложном напряженном состоянии приведены в работе [21]. Проведен вычислительный эксперимент на основе модели Патора ( Patoor ) [19] методом конечных элементов и представлены результаты. Статья [10] посвящена исследованию влияния предварительного деформирования на сдвиг температур превращения.

Эффект памяти формы и сверхупругость

В зависимости от температуры материал с памятью формы может находиться в двух модификациях (фазах): мартенситной (при низких температурах) и аустенитной (при высоких температурах). В аустенитной фазе кристаллическая решётка материала является кубической, в мартенситной – моноклинной [6]. При охлаждении материала, находящегося в аустенитной фазе, в зернах начинают зарождаться кристаллы мартенсита, постепенно заполняя весь объём сплава (рис. 1). Этот процесс начинается при температуре M s . Мартенситное превращение заканчивается при температуре M f , когда объемная доля мартенсита q становится равной единице (этап а – б ) (рис. 2). При последующем нагреве материала доля мартенсита уменьшается, начиная с температуры A s . Обратное превращение заканчивается при температуре А f , когда материал приходит в аустенитное состояние (этап в – г ) (см. рис. 2). Данный феномен называется эффектом памяти формы.

Для сплавов с памятью формы характерно также свойство сверхупругости, когда мартенситное превращение начинается при приложении к материалу напряжений при постоянной температуре. Эффект сверхупругости можно наглядно продемонстрировать в координатах «напряжение–температура» и «напряжение–деформация».

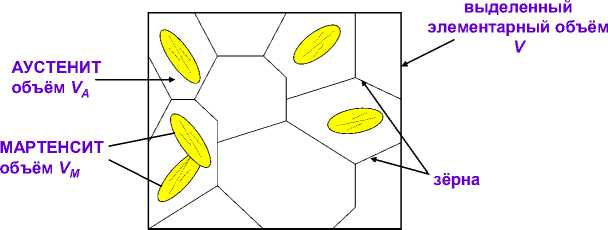
Рис. 1. Схематичное представление выделенного элемента объёма материала, состоящего из аустенитных и мартенситных зёрен [20]

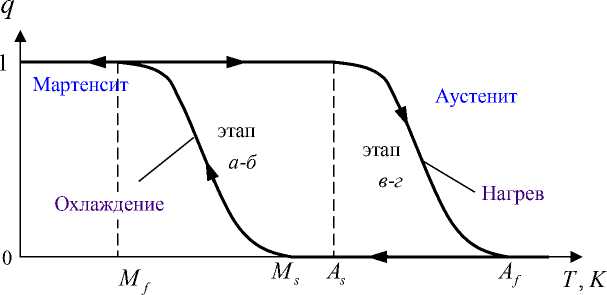
Рис. 2. Зависимость объемной доли мартенсита q от температуры T

а

б

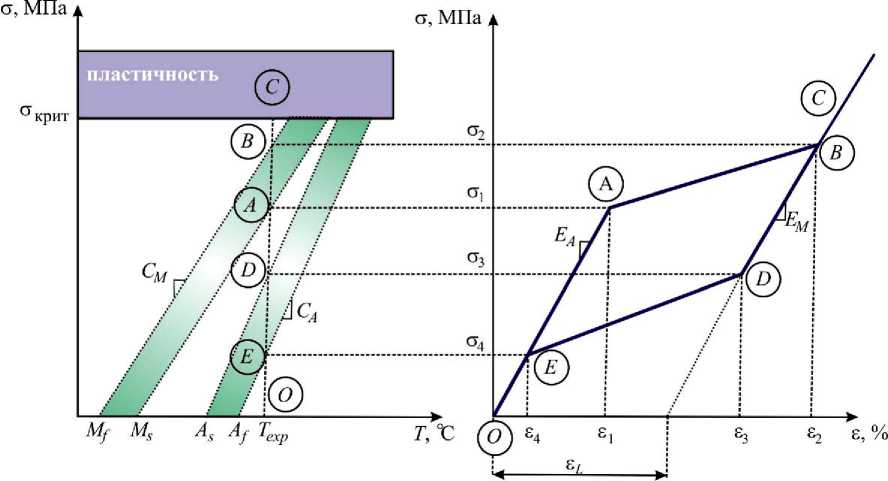
Рис. 3. Диаграммы, характеризующие сверхупругость: а – диаграмма σ– T , б – диаграмма σ–ε [15]

При нагружении материала при температуре T > A f сплав демонстрирует первоначально упругое поведение на участке ОА (рис. 3, а , б ). При приложении нагрузок к материалу происходит смещение температур прямого и обратного мартенситного превращений вправо по линейному закону (см. рис. 3, а ). При некотором напряжении о 1 температура становится равной M s и начинается мартенситное превращение. При напряжении о 2 оно заканчивается, при этом, если нагружать материал дальше, то при о = о _крит наступит пластичность, а затем -разрушение. На участке BD происходит упругая разгрузка. В точке D начинается обратное превращение, которое оканчивается в точке Е , соответствующей на графике температуре A f . В дальнейшем происходит разгрузка материала с модулем E A (участок Е – О ).

Эксперимент

Для исследования механического поведения материалов с памятью формы был проведен эксперимент на растяжение–сжатие для двух видов образцов при разных температурах и скоростях деформации.

Эксперименты проводились на образцах двух видов:

• 1)    стержень [длина – 150 мм, диаметр – 3 мм];

• 2)    образец стандартной формы (рис. 4) (табл. 1).

Образцы были вырезаны из никелид-титановой проволоки. Химический состав материала приведен в табл. 2. Эксперимент проводился в Центре экспериментальной механики Пермского государственного технического университета. Механические испытания проводились на универсальной испытательной машине Instron (Инстрон)-5882. Общий вид машины показан на рис. 5.

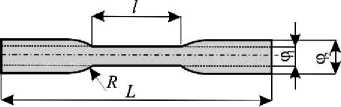
Рис. 4. Образец стандартной формы

Таблица 1

Размеры образца

Наименование размера	L	l	R	φ 1	φ 2
Значение, мм	78	26	2,5	2	3

а                                               б

Рис. 5. Машина для испытаний Instron- 5882: а – общий вид устройства, б – панель управления

Рис. 6. Образцы в захватах: а – стержень, б – образец стандартной формы

Таблица 2

Химический состав сплава из никелида титана

Название элемента	Ni	Ti	C	O	N	Cu
Доля, %	55	баланс	0,05	0,045	<0,001	<0,001

Стержневые образцы (рис. 6, а)

Эксперименты на стержневых образцах включали в себя следующие испытания:

• •    испытание на растяжение-сжатие образцов при 23°С;

• •    испытание на растяжение-сжатие образцов при 40°С;

• •    испытание на растяжение-сжатие образцов при 55°С.

Методика эксперимента

Образец зажимался в плоских захватах с максимальным усилием в термокамере при температуре испытания, затем устанавливалась предварительная нагрузка. Далее задавалась программа испытания по удлинению образца (перемещению траверсы) до 8 мм со скоростью 0,5 мм/мин и затем разгрузка с той же скоростью с управлением по перемещению траверсы до нулевой нагрузки. Измерение деформации проводилось по видеоэкстензометру.

Результаты испытаний показаны на рис. 7. Можно заметить, что с увеличением температуры наблюдается рост величины напряжений, которые развивает образец при прямом превращении. В испытаниях с более высокой температурой при разгрузке наблюдается уменьшение остаточной деформации по сравнению с экспериментами при меньшей температуре.

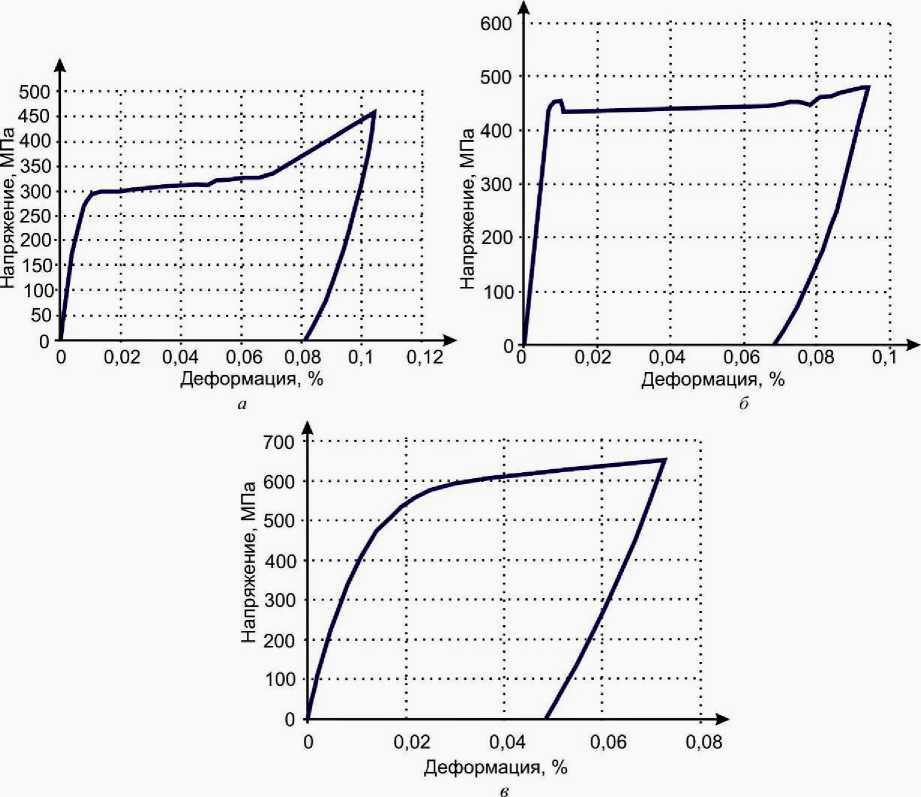
Рис. 7. Результаты испытаний стержневых образцов из никелида титана при разных температурах: а – 23°С, б – 40°С, в – 55°С

Образцы стандартной формы (рис. 6, б)

Эксперименты на образцах стандартной формы включали в себя следующие испытания (табл. 3):

• 1)    испытание на растяжение-сжатие образцов при 23°С (рис. 9);

• 2)    испытание на растяжение-сжатие образцов при 42°С (рис. 10);

• 3)    испытание на разрыв образцов при 90°С (рис. 8);

• 4)    испытание на растяжение-сжатие образцов при 90°С с разными скоростями нагрузки-разгрузки (рис. 8).

Таблица 3

Виды и характеристики испытаний образцов стандартной фо			рмы
Номер образца	Вид испытания	Скорость нагрузки/разгрузки, с–1	Осевая измерительная база, мм
1.03	испытания на разрыв	1,3∙10–4	21,86
2.01	растяжение–сжатие	1,3∙10–4	20,65
2.02	растяжение–сжатие	1,3∙10–4	19,99
3.01	растяжение–сжатие	2,5∙10–5	20,46
5.01	растяжение–сжатие	1,3∙10–4/ 1,3∙10–6	16,38

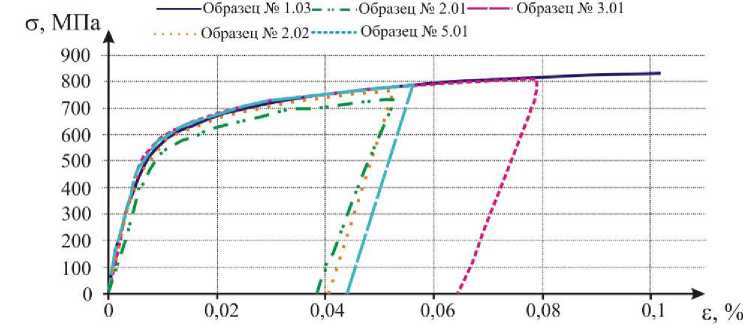
Рис. 8. Результаты испытаний образцов стандартной формы (см. табл. 3)

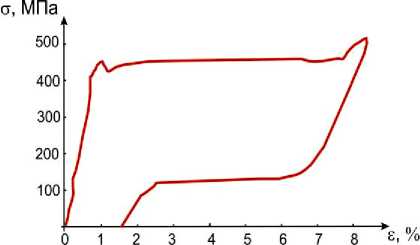
Рис. 9. Результаты деформирования образцов стандартной формы при 23°С

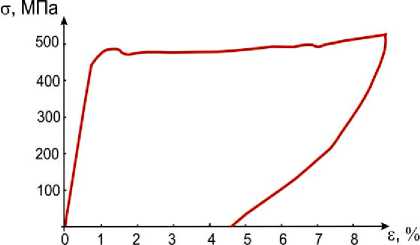
Рис. 10. Результаты деформирования образцов стандартной формы при 42°С

В результате экспериментов было выявлено, что температура испытаний имеет большее влияние на гистерезис образцов по сравнению со скоростью деформирования. При высоких температурах (90°С) материал ведёт себя подобно обычным сталям, это обусловлено тем, что разрушение материала происходит раньше, чем начнутся фазовые превращения (см. рис 3, а ). При температурах 23°С и 42°С материал в полной мере проявляет свойство сверхупругости и памяти формы.

Модели

Модель Мовчана [4]

Микромеханический подход Мовчана заключается в рассмотрении зарождения и развития кристаллов мартенсита, которые вносят определенный вклад в скорость изменения фазовой деформации в сплаве с памятью формы. Макроскопическая деформация является суммой вкладов микродеформаций р , вычисленных по параметру q (доля мартенсита). Предполагается, что скорость роста кристаллов мартенсита пропорциональна накопленной фазовой деформации и уровню напряжений. В модели учитываются различные упругие свойства аустенита и мартенсита.

Общая схема подхода изложена в статье [4]. Система определяющих соотношений формулируется следующим образом:

уф

ij ij ij , dаф = (c0rfj + a0аф)dq при dq > 0,

ds ф =

q₁ = cos

q ₂ = cos

a 0 ^s ij

^(ex P ⁽ a 0 ) ^- 1)

+ a 0 s ф dq

nf T - k \° ij ° ij - Mf

2 M_s - M_f

к S f 7

nf T - k x° ij ° ij - as

2 A_f - A_s

к f S 7

при dq <  0,

при dq >  0,

при dq <  0,

¹ = q + ^{1 -} q

E(q)   E1   E2 , где sу,sф - тензоры упругой и фазовой деформации, Е1, Е2 - значения модуля Юнга для мартенситного и аустенитного состояния; a0, k, c0 – коэффициенты материала, которые можно найти из опыта на прямое превращение. Уравнения (2) и (4) соответствуют прямому превращению, а (3) и (5) – обратному. Методика определения коэффициентов модели Мовчана представлена в работе [5].

Модель Патора [19, 20]

Модельный объект представляет поликристалл, состоящий из зерен. Зерна рассматриваются в выделенном элементарном объёме. Каждое зерно рассматривается как монокристалл, в котором может образовываться 1,2,… N вариантов мартенсита (под вариантом в данном случае подразумевается мартенситная пластина). Внутри выделенного элементарного объёма происходит мартенситное превращение, обусловленное механическим или температурным нагружением. Поэтому в качестве управляющих переменных были взяты макроскопическое напряжение Σ и температура Т . Предполагается, что упругие модули C ijkl одинаковы для обеих фаз.

Эволюция макроскопической деформации E ij определяется изменением термодинамического потенциала Гиббса ψ , который является функцией управляющих параметров (тензора напряжений S j и температуры Т) и системы внутренних переменных f (объёмная доля мартенсита):

T ) = 12. .С7^г_иЕ_и + TL.8^Tf-B(T-TAf-TH ё^т£^т X². (7) ψ ij ^,,, ij ₂ ij ijkl kl ij ij                  0        ₂ зерна ij ij         ₂ варианта ^.

Функция Лагранжа в этом случае записывается в виде

L ( S j , T , f , s т ) = V( S j , T , f , s TT ) + ^ 0 f -^ i ( f — 1) — ^ 2 ( S T q -s ma _X),           (8)

где множители Лагранжа связаны с долей мартенсита и средней деформацией фазового перехода:

X _o(0 - f ) = 0, X i ( f - 1) = 0, X 2 ( s _e ^T q -s max ) = 0.                     (9)

Минимум функции Лагранжа достигается в точке ( f , s T ), где градиент равен нулю. При дифференцировании функции Лагранжа по внутренним переменным (доля мартенсита f и средняя деформация фазового перехода s T ) можно получить термодинамическую силу ( F f- ) и силу ориентации ( F _s i ):

TT      TT f     df \ у, , J , j / ij ij xО/ зерна ij ij J        варианта./       0 ч ,

F.

5 L

д.

дёт„

£j , T , f , . T ) = S y f - H . f — H _ва ри _а нт _а f — Z . ^ .

Предполагается, что когда термодинамическая сила F f достигает критического значения, начинается рост мартенситных пластин. При достижении силой ориентации F _{8 (}. некоторого критического значения начинается переориентация зерен мартенсита.

Модель Лангелара [13]

Рассматривается одномерная модель, описывающая поведение материала с памятью формы. В модели делается предположение, что поскольку кривые при нагрузке и разгрузке практически одинаковые, и описать их можно одинаково. Предположение позволяет пренебречь гистерезисом. Вследствие сделанного предположения доля мартенсита ξ является функцией напряжения σ и температуры Т, т.е. ξ=ξ (σ,T). Определяющее соотношение, связывающее напряжение и деформацию, имеет вид с = E Ое-8 ma1 ^),                           (12)

где е - деформация, E ( ^ ) - эффективный модуль, 8 mm^ax - максимальная деформация фазового превращения. Эффективный модуль зависит от доли мартенсита, так как сплав – смесь двух «материалов» с разными свойствами. Предполагается, что текущая деформация превращения пропорциональна доле мартенсита ξ . Для того чтобы улучшить согласование графиков модели с экспериментальными данными и в то же время упростить модель, была предложена следующая модель для описания одномерного поведения материала:

• 8    < 81 : С = Еа 8с = <81 < 8 < 82 : С1 = ET (8 - 81) + Со (81),

  
  

• ⁸    > ⁸ 2 ^{: С} 2 = ^ER ^{( 8-8} 2 ) ^{+ С} 1^{( 8} 2 ),

где E A и E R - постоянные параметры, 8 1 , 8 2 , E_T - линейные функции температуры.

8 1 ( T ) = K 8 ( T - Т о ) +8 о ,

8 2 ( Т ) = 8 1 ( Т ) +Д ,                                       (14)

E t ( Т ) = K e (Т - Т о ) + E о .

Модель содержит 8 параметров K ₈ , K_E , 8 _о, Д , E _о, E A , E R , Т _о и может быть обобщена для трёхмерного случая.

Модель Ауриччио [7]

В рассматриваемой одномерной модели Ауриччио рассматривается 3 вида фазовых превращений:

• 1)    прямой фазовый переход ( А → М );

• 2)    обратный фазовый переход ( М → А );

• 3)    переориентация мартенсита ( М → М ).

В качестве внутренней переменной выбирается относительная доля содержания мартенсита ^ S .

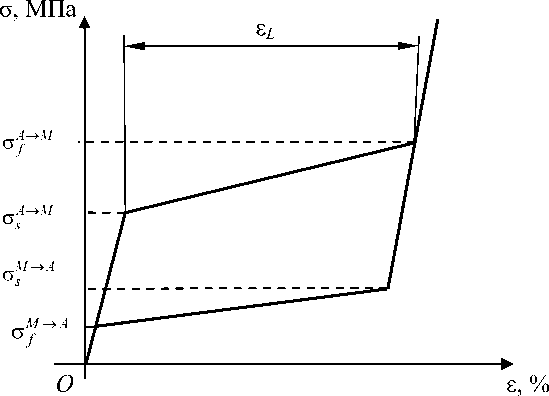
Рис. 11. Характеристические напряжения в модели Ауриччио на схематической диаграмме растяжения-сжатия материала c памятью формы

Прямое фазовое превращение согласно модели Ауриччио описывается следующим образом:

^1

ξ S = (1 -ξ S )       A → M .                              (15)

σ-σ _f

Обратное превращение происходит по закону:

й|

ξ S =ξ S       _{M → A} .                               (16)

σ-σ _f

Напряжения σ ^A _f ^{→ M} и σ ^M _f ^{→ A} обозначают напряжения окончания прямого и обратного превращения соответственно (рис. 11). Полная деформация раскладывается на упругую и неупругую составляющие:

ε =ε ^e + ε L ξ S ,                                      (17)

где ε ^e – упругая деформация, ε _L – максимальная фазовая деформация.

Модуль упругости определяется как

E =       ^{E A}      ,                             (18)

1 + ( ^{E A} - 1) ξ S

EM где EA,EM – значения модуля Юнга для аустенитного и мартенситного состояния.

Сравнение моделей

Большое разнообразие определяющих соотношений, которые позволяют описывать различные эффекты, возникающие при фазовых переходах в сплавах с эффектом памяти формы, повлекло за собой проблему выбора уравнений, адекватно моделирующих поведение конструкций из данных материалов. В некоторых случаях, например в задачах управления, предпочтительнее использовать модели с явным аналитическим выражением, связывающим напряжения и деформации в материале. В основном развиты численные модели, заложенные в коммерческих пакетах, например в

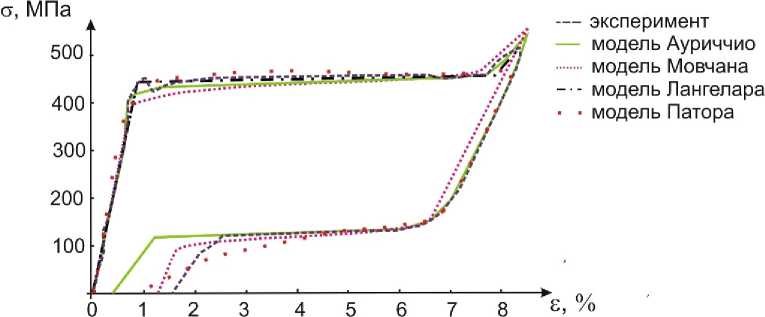
Рис. 12. Кривые в координатах напряжение-деформация для сплава с памятью формы: экспериментальная кривая при температуре Т =23ºС и результаты, полученные по моделям

ANSYS . В данной работе были проанализированы следующие модели: модель Мовчана, модель Лангелара, модель Патора и модель Ауриччио.

В результате сравнения моделей с данными эксперимента на растяжение-сжатие образца из никелида титана при температуре 23ºС показано, что все четыре модели адекватно описывают поведение материала. Однако модель Лангелара не учитывает гистерезисное поведение материала и позволяет описать лишь превращение аустенит → мартенсит. Модель Ауриччио удобна тем, что она используется в программе ANSYS и предпочтительна при инженерных расчётах конструкций сложной формы. Модель Патора также может быть заложена в программу ABAQUS , основанную на расчетах методом конечных элементов. Все рассмотренные модели способны описать трехмерное напряженно-деформированное состояние. Достоинство модели Мовчана заключается в наличии аналитических решений, которые используются при решении задач управления собственными деформациями. Значения параметров моделей представлены в табл. 4, 5, 6, 7.

Таблица 4

Свойства материала из сплава с памятью формы по модели Ауриччио

	1	2
Температура испытания, °С	23	42
Напряжение начала прямого превращения ( σ s A → M ), МПа	412	536
Напряжение окончания прямого превращения ( σ A f → M ), МПа	473	571
Напряжение начала обратного превращения ( σ s M → A ), МПа	150	256
Напряжение окончания обратного превращения ( σ M f → A ), МПа	112	97
Максимальная остаточная деформация (ε L )	0,83	0,88
Параметр, характеризующий разницу между поведением материала при растяжении и сжатии (α)	0,12	0,15
Модуль Юнга мартенситной фазы ( Е М ), МПа	11000	7900
Коэффициент Пуассона (ν)	0,3	0,3

Свойства ма Параметр	териала из сплава с памятью формы п Значение	Таблица 5 модели Мовчана Единица измерения
E a	47058	МПа
E m	10889	МПа
k	8,38	°С/МПа
c 0	2∙10–4	1/МПа
a 0	3,36	–
M s	5	°С
M f	–8	°С
A s	10	°С
A f	18	°С

Таблица 6

Свойства материала из сплава с памятью формы по модели Патора
Параметр	Значение	Единица измерения
T 0	6,5	°С
B	0,0235	МПа/°С
H зерна	1181,49	МПа
H варианта	571,266	МПа
E	15789,45	МПа
M s	5	°С
M f	–8	°С
A s	10	°С
A f	18	°С

Таблица 7

Свойства материала из сплава с памятью формы по модели Лангелара

Параметр	Значение	Единица измерения
K ε	–3,987	°С–1
E 0	189,462	МПа
E A	47639,281	МПа
ER	10992	МПа
ε 0	9,55	–
K E	2,041	МПа∙°С–1
∆	0,951	–
T 0	32,526	°С

Заключение

Устройства из никелида титана применяются в медицине много лет. Проблема заключается в том, что врачи в основном полагаются на свой клинический опыт. Поэтому возникает необходимость объективизации эмпирически разработанных методик лечения, а также индивидуального предоперационного планирования на основе биомеханического моделирования. Для биомеханического анализа того или иного медицинского устройства необходимо знать свойства материала, из которого он изготовлен. В данной работе исследуется механическое поведение сплава, из которого изготовлены фиксаторы, применяемые в челюстно-лицевой хирургии.

В работе был проведён эксперимент на образцах двух видов: показано, что температура испытаний имеет большее влияние на гистерезис по сравнению со скоростью деформирования. Получен типичный гистерезис при температурах 23°С и 42°С.

Рассмотрены модели, описывающие поведение материалов с памятью формы. Результаты вычислений сравнены с экспериментом.

Результаты испытаний сплавов будут использованы при исследовании механического поведения фиксаторов с памятью формы, использующихся в челюстнолицевой хирургии [2, 3, 14].

Благодарности

Работа выполнена при поддержке РФФИ № 07–01–96061-р-Урал-а и Федерального агентства по науке и инновациям в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2012 годы» (гос. контракт № 02.518.11.7135).

Металлургия, 1990.