Экспериментальное исследование ТЕМ-рупора с неоднородным диэлектрическим заполнением

ТЕМ-рупоры получили широкое распространение, как одна из основных составляющих систем сверширокополосных (СШП) радиосистем. В первую очередь, это вызвано простотой конструкции таких антенн и удовлетворительными характеристиками направленности и согласования. Известны некоторые общие способы улучшения этих характеристик: изменение формы и угла раскрыва антенны [1–6]. В этих работах основной акцент делается на уменьшение нижней граничной частоты антенны. Однако, известны факторы, ограничивающий частотный диапазон сверху, главным из которых является не-синфазность излучения в плоскости раскрыва антенны, приводящий к искажению диаграммы направленности. Частично данную проблему решает использование диэлектрических линз, помещаемых между лепестками рупора [4; 5].

Данная работа посвящена решению проблемы искажения диаграммы направленности и расширения диапазона рабочих частот ТЕМ-рупора. Предлагаемый метод заключается в создании искусственного материала с диэлектрической проницаемостью, изменяющейся в зависимости от направления распространения электромагнитной волны в пространстве между лепестками антенны.

1. Аналитическое выражение для диэлектрической проницаемости заполняющей структуры

Варьирование диэлектрической проницаемостью б позволяет предотвратить распад диаграммы направленности в верхнем частотном диапазоне за счет выравнивания волнового фронта, распространяющийся между лепестками антенны. В целом, данная идея базируется на предположении о существовании точечного фазового центра, в котором возбуждается электромагнитная волна. Диэлектрическая проницаемость среды выбирается так, чтобы обеспечить одинаковое время прихода электромагнитной волны к плоскости раскрыва ТЕМ-рупора.

Опуская подробный вывод выражения для распределения б в зависимости от угла распространения луча, можем воспользоваться выражением, полученным в работе [7], которое наиболее просто выглядит для случая равенства длины и ширины раскрыва антенны:

^б ( ф ) = ^Б тах ^cos2 ( ф ) ,                                ⁽¹⁾

где ф — угол отклонения луча от главного направления излучения, а Б тах — наибольшая диэлектрическая проницаемость, достигаемая в главном направлении.

Если же раскрыв рупора не является квадратным, как представлено на рис. 1, то выражение

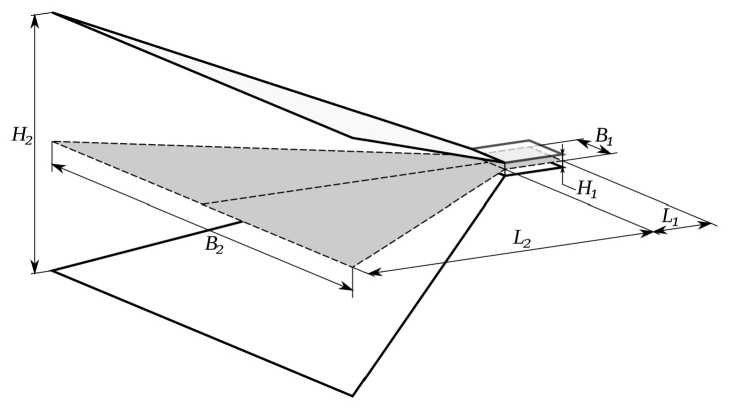
Рис. 1. Внешний вид и геометрические размеры ТЕМ-рупора

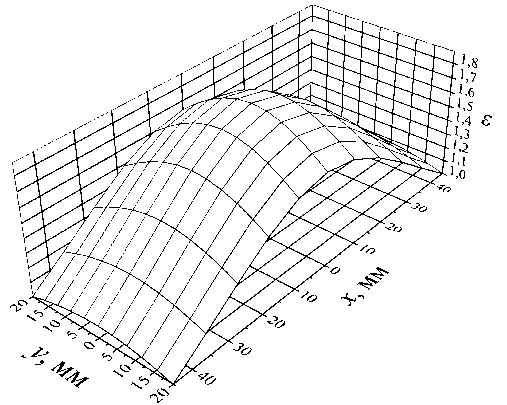
Рис. 2. Распределение диэлектрической проницаемости £ для геометрических размеров ТЕМ-рупора: L 1 = 10 мм, L 2 = 50 мм, B 1 = 10 мм, B 2 = 90 мм, H = 2 мм, H 2 = 40 мм

(1) преобразуется, и для плоскости апертуры

можно записать:

£ ( x , У ) =

( H 2 2 ) 2 + ( B 2 2 ) 2

+ ⁽ L 2 ⁺ p ) 2

x ² + у ² + ( L 2 + p )²

где х и у – координаты отклонения точки на плоскости раскрыва от центра (в обозначениях рис. 2), а р – расстояние от плоскости перехода линии запитки в лепестки до фазового центра. Следует отметить, что выражение (2) определялось исходя из того, чтобы при максимальном отклонении от оси рупора £ = 1.

В данной работе в качестве примера использовались следующие геометрические размеры: L 1 = 10 мм, L = 50 мм, B 1 = 10 мм, B 2 = 90 мм, H 1 = 2 мм, H 2 = 40 мм, распределение £ для которых приведено на рис. 2.

2. Синтез структуры с распределенной диэлектрической проницаемостью

Очевидно, что создание структуры с непрерывно изменяющейся диэлектрической проницаемостью представляется, на сегодняшний день, весьма затруднительным. Один из возможных вариантов решений данной проблемы описан в [7], где пространство между лепестками антенны было заполнено косоугольными пирамидами с разной диэлектрической проницаемостью, вершины которых лежали в фазовом центре. Таким образом, пространство неоднородной структуры представляется большим числом областей с постоянной диэлектрической проницаемостью. Такой подход является приемлемым для описания антенны при моделировании, но не для изготовления.

В данной работе предлагается другой способ формирования переменной диэлектрической проницаемости, который состоит в использовании перфорированного диэлектрика. Предполагается, что его можно считать вспененным диэлектриком, подчиняющимся логарифмическому закону смещения, а диэлектрическую проницаемость описывать формулой Лихтенеккера [8]. Вспененный диэлектрик представляет собой неупорядоченную смесь с воздухом некоторого материала с диэлектрической проницаемостью £_диэл и объемной концентрацией Q _диэл. Опуская очевидные выкладки можно записать:

^£ = exp ⁽ Q диэл In ^£ диэл ) . ⁽³⁾

Создание вспененного материала, с переменным и контролируемым отношением объемов диэлектрика и воздуха в настоящее время не представляется возможным. Однако для числен-

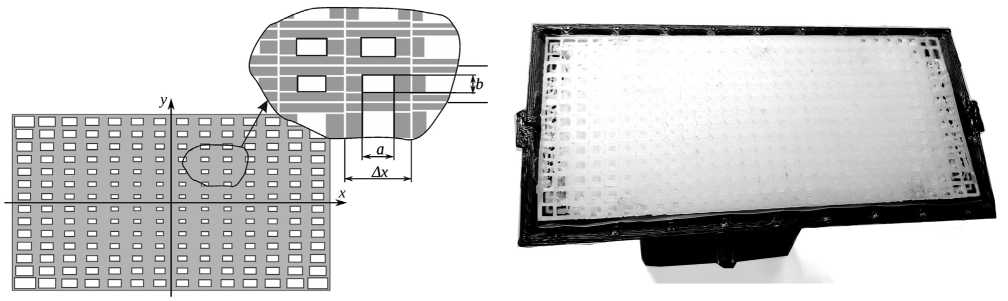
б )

а )

Рис. 3. Пример одного слоя неоднородной диэлектрической среды ( а ) и ее фотография ( б )

ных расчетов и дальнейших экспериментов была использована следующая модель: Пространство внутри антенны было разбито на слои толщиной 0,4 мм. Каждый слой делился на ячейки размером не менее 3 х 3 мм (A x и А у в обозначениях рис. 3, а ), в центре которых определялась диэлектрическая проницаемость по формуле (2). Затем в данной ячейке перфорировалась (заполнялась воздухом) центральная область. Для удобства в качестве такой воздушной полости выбирался параллелепипед со сторонами: а = k A x и b = k А у (рис. 3, а ), где A x и А у — размер ячейки, а k определяется по формуле:

| ln Б | 2

к = 1 —              ,                                 (4)

• V ^Б диэл )

• 3. Исследование ТЕМ-рупора

где Б диэл — диэлектрическая проницаемость диэлектрика, б — диэлектрическая проницаемость, которую требуется получить в центре ячейки. Таким образом, в общем случае коэффициент k является функцией координат x ,y ,z . Следует также отметить, что A x и А у постоянны в пределах каждого слоя и вычисляются исходя из его высоты и ширины так, чтобы были не меньше 3 мм. Данный размер был выбран исходя из ограничений технологии изготовления неоднородной диэлектрической среды.

с неоднородным диэлектрическим заполнением

Для синтеза предложенного неоднородного диэлектрического заполнения была написана программа, генерирующая трехмерную модель в виде файла в формате STL (^^^^^^ ^^^^^^^^-p^y). Электродинамическое моделирование производилось с использованием метода конечных разностей во временной области (FDTD) [9]. Для симуляции пространства за пределами счетного объема использовались граничные условия типа PML (p^^f^c^^y m^^c^^d ^^y^^) [10; 11] (4 слоя), где расстояние от проводящей структуры до границы счетного объема поддерживалось не менее 20 мм.

Предложенная структура (рис 3, б ) также была изготовлена по технологии FDM (fu^^d d^p^^^^^^n m^d^^^n^) при помощи 3D-принтера M^k^^B^^ R^p^^c^^^^ 2X. В качестве материала использовалась нить из полистирола.

Основными характеристиками, которые рассчитывались при моделировании являлись затухание несогласованности по входу (^^^u^n loss) и коэффициент усиления антенны. Экспериментальное исследование этих характеристик проводилось при помощи векторного анализатора цепей A^^^^n^ PNA-L 5230C.

На рис. 4, а приведены зависимости затухания несогласованности по входу (^^^u^n loss) для антенны без заполнения неоднородной диэлектрической средой. Из графиков видно хорошее согласование расчетных и экспериментальных характеристик. Наблюдаемое расхождение в диапазоне от 13 до 17 ГГц объясняется тем, что в реальном устройстве присутствовали коаксиально-полосковый переход и симметрирующее устройство, несколько улучшающие согласование в данном диапазоне.

На рис. 4, б приведены зависимости затухания несогласованности по входу (^^^u^n loss) для антенны с заполнением пространства между лепестками неоднородной диэлектрической средой. В случае моделирования наблюдается улучшение согласования в нижней области, а именно уменьшение нижней граничной частоты по уровню –10 дБ с 4,4 ГГц до 2,3 ГГц. При этом в эксперименте удовлетворительное согласование (< -10 дБ) по входу антенны наблюдалось от 2,3 до 26,2 ГГц.

а )

б )

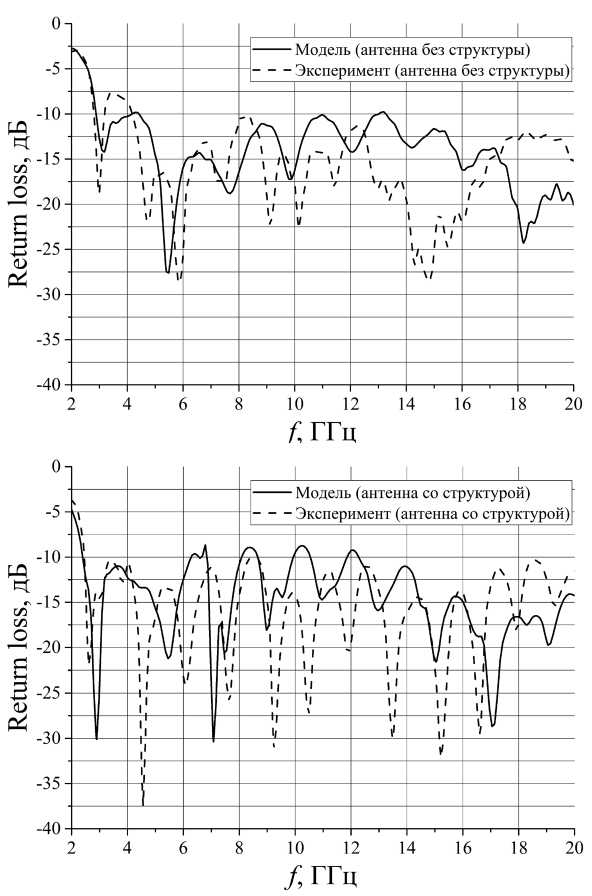
Рис. 4. Расчетные и экспериментальные зависимости R^^u^n L^^^ (затухания несогласованности) для антенны без ( а ) и с ( б ) неоднородным диэлектрическим заполнением

/,ГГц

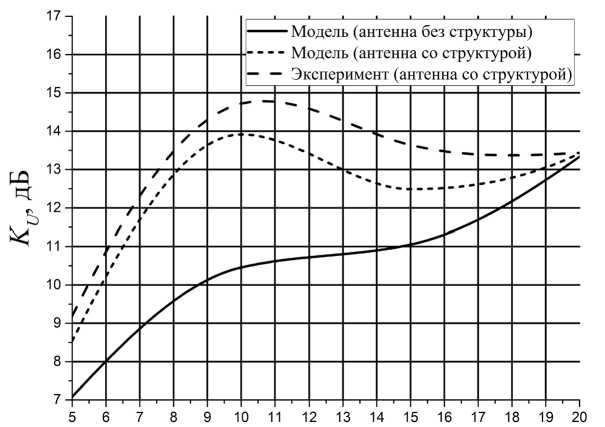
Рис. 5. Зависимость коэффициента усиления антенны от частоты

На рис. 5 приведены частотные зависимости коэффициента усиления K _U в главном направлении. Как видно из графиков при использовании неоднородной диэлектрической среды удается получить выигрыш в направленности антенны от 1,5 дБ на 5 ГГц до 3,5–4 дБ в области 10 ГГц. Несмотря на то, что в верхнем частотном диапазоне (от 17 до 20 ГГц) прирост коэффициента усиления выглядит незначительным, диаграмма направленности антенны в случае использования неоднородной диэлектрической структуры существенно улучшается: предотвращается расщепление диаграммы направленности и резко возрастает коэффициент подавления боковых лепестков.

Расхождения расчетной и экспериментально измеренной зависимостей коэффициента усиления антенны объясняется тем, что при изготовлении неоднородной диэлектрической среды использовался метод FDM печати, которому характерно неизбежное отклонение от геометрических размеров трехмерной модели за счет температурного сжатия и расширения материала.

Заключение

В работе предложено неоднородное диэлектрическое заполнение пространства между лепестками ТЕМ-рупора. Несмотря на сложность изготовления, такая среда позволяет улучшить характеристики согласования и направленные свойства антенны. Наиболее существенным эффектом применения неоднородное диэлектрического заполнения для примера, приведенного в работе, является уменьшение нижней границы рабочего диапазона на 2 ГГц по уровню –10 дБ и рост коэффициента усиления в среднем на 3 дБ. Кроме того начиная с 10 ГГц удалось уменьшить уровень боковых лепестков и предотвратить искажение диаграммы направленности за счет не-синфазности излучения в плоскости раскрыва.

В работе также изложена методика построения трехмерной модели предложенной неодна-родной диэлектрической среды, которая может быть изготовлена с помощью технологий трехмерной печати. Экспериментально измеренные характеристики достаточно хорошо согласуются с результатами моделирования.

Работа выполнена в рамках гранта Президента Российской Федерации для государственной поддержки молодых российских ученых – докторов наук (МД-7902.2016.9).