Экспериментальное исследование влияния поршневых колебаний на динамику двойной диффузии в ячейке Хеле–Шоу

Двойная диффузия представляет собой тип конвективной неустойчивости, возникающей в стратифицированной жидкой среде, плотность которой зависит от вертикального распределения двух (или более) скалярных компонентов с различными коэффициентами молекулярной диффузии. Ключевым условием формирования неустойчивости является наличие компонента, формирующего неустойчивый (в поле тяжести)

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

градиент плотности, который стабилизируется за счет устойчивого градиента плотности, формируемого другим компонентом. Классическим примером такой среды является термохалинная стратификация в океане, где в качестве диффундирующих компонентов выступают тепло и соль, скорости диффузии которых отличюется примерно на два порядка. Это различие обуславливает развитие конвективного течения в виде пальчиковых структур, существенно влияющих на вертикальный перенос массы, питательных веществ и стратификацию воды в океанических системах [1]. Тип возникающей конвекции определяется тем, какой из компонентов диффундирует быстрее. Если быстрее распространяется неустойчиво распределенный компонент, формируется конвекция двойной диффузии (англ. fingering regime of double diffusive instability ). Такой режим характерен для тропических широт, где поверхностные воды теплые и соленые. В противоположной ситуации, когда быстрее распространяется компонент с устойчивым градиентом, формируется конвекция диффузионного слоя (англ. diffusive regime of double diffusive instability ), наблюдаемая в полярных регионах, где поверхностные воды холодные и менее соленые в результате таяния льда.

История изучения двойной диффузии началась с феномена «вечного соляного фонтана» [2]. Согласно гипотезе авторов, при подаче холодной менее соленой воды через вертикальную трубу в более теплую и соленую окружающую среду может возникнуть устойчивый самоподдерживающийся восходящий поток. Механизм этого явления связан с двумя конкурирующими процессами. Когда холодная вода попадает в трубу, она начинает нагреваться от более теплой окружающей среды через стенки. По мере нагрева плотность воды уменьшается, и она устремляется вверх. Вместе с этим соль из окружающей соленой жидкости постепенно диффундирует в трубу, увеличивая плотность поднимающейся нагретой воды. Однако вследствие большой разницы в скорости диффузии тепла и соли вода в трубе прогревается быстрее, чем становится соленее. Таким образом, нагретая вода остается легче окружающей жидкости и продолжает всплывать, формируя соляной фонтан. Экспериментальное подтверждение данного механизма [3] стало основой для развития теоретических моделей [4–6], а также прикладных задач [7–10]. Подробнее с многочисленными исследованиями можно ознакомиться в обзорах [11–13].

Особый практический интерес представляет применение эффекта двойной диффузии в технологиях искусственного апвеллинга – управляемого подъема глубинных вод, обогащенных питательными веществами. Данная технология, основанная на механизме «соляного фонтана», была успешно протестирована и реализована в Японии с начала 2000-х гг. [14; 15]. С учетом значимости апвеллинга для морских экосистем актуальной задачей является разработка методов управления его интенсивностью. Одним из перспективных инструментов управления является вибрационное воздействие, создаваемое контролируемыми пульсациями давления в гидравлических системах апвеллинга. Известно, что вибрационное воздействие способно существенно модифицировать поведение стратифицированных и многокомпонентных жидких сред [16]. Одним из ключевых эффектов вибрационного воздействия является ориентирующее действие, способствующее выравниванию градиентов плотности вдоль направления колебаний, что приводит к деформации межфазных и диффузионных границ [17–19]. Кроме того, вибрации могут стабилизировать систему, повышая порог возникновения различных типов конвекций, включая термокапиллярную конвекцию Марангони [20], конвекцию Рэлея – Тейлора [21] и Рэлея – Бенара [22]. Напротив, горизонтальные вибрации часто усиливают неустойчивости, приводя к нарушению стратификации и способствуя формированию новых типов течений [18; 23]. Во вращающихся системах при совпадении частоты внешнего воздействия с собственными модами колебаний системы могут возникать резонансные явления, способные снижать устойчивость и возбуждать инерционные волны, что приводит к модуляции течения и направленному массообмену [24].

Многочисленные исследования подтвердили, что вибрации существенно влияют на режимы двойной диффузии. При этом эволюция конвекции зависит от геометрии системы, частоты, амплитуды и направления колебаний. Показано, что низкочастотные вертикальные вибрации, как правило, усиливают неустойчивость и ускоряют перемешивание [25–28], тогда как высокочастотные могут стабилизировать систему, что выражается в увеличении значения критического числа Рэлея и, как следствие, смещении границ устойчивости. Эти эффекты подтверждены численным моделированием [29–31], в рамках которого также продемонстрировано, что вертикальные вибрации влияют на форму пальчиковых структур, степень их упорядоченности и время формирования, в ряде случаев отсрочивая или подавляя их развитие. Аналогичный эффект упорядочивания пальчиковых структур был обнаружен экспериментально в реакционной системе [32]. Кроме того, высокочастотные колебания могут индуцировать вторичные неустойчивости [33; 34], а при определенном соотношении частоты и амплитуды – вызывать сложное бифуркационное поведение [35].

Особый интерес представляют колебания поршневого типа, при которых жидкость осциллирует вдоль внутренних стенок неподвижного резервуара. Такая постановка моделирует пульсации давления в трубах систем апвеллинга. Случай чисто диффузионного смешения двухслойной системы жидкостей при вертикальных поршневых колебаниях был экспериментально исследован в [36]. Показано, что колебания значительно усиливают массоперенос за счет дисперсии Тейлора – явления, при котором колебательные потоки усиливают механизм диффузионного распространение вещества за счет взаимодействия с градиентами концентрации вдоль направления течения. Случай влияния поршневых колебаний на динамику конвекции двойной диффузии был впервые экспериментально исследован в [37]. Анализ скорости движения пальчиковой структуры и динамики толщины диффузионной зоны смешения показал, что вертикальные поршневые колебания значительно увеличивают скорость массопереноса по сравнению с покоящейся системой.

Хотя данные [38] косвенно подтверждают усиление конвекции двойной диффузии под действием поршневых колебаний, влияние амплитуды и частоты вибраций на скорость перемешивания остается неизученным. Настоящая работа направлена на восполнение данного пробела. В рамках исследования экспериментально изучено влияние вертикальных поршневых колебаний на динамику двухслойной системы смешивающихся жидкостей в ячейке Хеле-Шоу, в условиях развития конвекции двойной диффузии. Особое внимание уделяется анализу геометрии, пространственной организации и эволюции пальчиковых структур. Для количественной оценки степени перемешивания исходных слоев используется параметр смешения M , который рассчитывается на основе изменения стандартного отклонения яркости изображений. На основе полученных временных зависимостей M ( t ) проводится расчет эффективного коэффициента диффузии D eff . Показано, что поршневые колебания ускоряют перемешивание слоев и усиливают апвеллинг, способствуя вертикальному переносу растворенных веществ, что имеет биофизическое значение, так как интенсифицирует доставку питательных веществ к планктону и другим микроорганизмам, живущим вблизи поверхностей или в локальных микросредах, где обмен веществ ограничен.

Материалы и методы

Экспериментальная установка

Эксперименты выполнены на вибрационном стенде, состоящем из вертикальной ячейки Хеле-Шоу, гидравлического контура, который обеспечивал вертикальные поршневые колебания двухслойной системы смешивающихся жидкостей в канале и системы управления. Ячейка образована двумя симметричными половинами. Схематическое изображение установки, включая одну из половин ячейки, представлено на рис. 1.

Каждая половина ячейки Хеле-Шоу состоит из орг-стеклянной рамки, в центральной части которой вклеено заподлицо стеклянная пластина 2 высотой 16 см, шириной 9 см и толщиной 1 см. Толщина и форма рабочей полости ячейки задается силиконовым вкладышем 3 , который устанавливается между оргстеклянных рамок. В настоящем эксперименте вкладыш имел толщину 0,1 ± 0,01 см. На рис. 1 форма вкладыша выделена красной сплошной линией. В верхней и нижней частях оргстеклянных рамок имеются специальные углубления

4 , выполняющие функцию расширительных объемов для снижения гидродинамического сопротивления жидкости при ее колебаниях внутри ячейки. Конструкция ячейки также предусматривает систему подачи и отвода рабочих жидкостей, которая использовалась для формирования двуслойной системы жидкостей перед началом эксперимента. Для этого в ячейке предусмотрено четыре отверстия. Пара отверстий 5 располагается в расширительных объемах и использовалась для подачи жидкостей, другая пара отверстий 6 расположена в центральной части торца вкладыша и предназначена для отвода жидкостей из зоны контакта слоев. Все отверстия соединены со шприцевым насосом 7 , который обеспечивает синхронный процесс подачи и отвода рабочих жидкостей, что позволяет формировать тонкую горизонтальную линию контакта между слоями двуслойной системы.

Вертикальные колебания жидкой системы в неподвижной ячейке Хеле-Шоу создаются гидравлическим контуром 8 , который включает в себя линейный двигатель прямого привода 9 , соединенный с мембранным насосом тягово-натяжного типа 10 . Насос состоит из двух камер 11 , заполненных водой и разделенных гибкой резиновой мембраной 12 толщиной 0,1 см. Колебания штока 13 двигателя заданной частоты f и амплитуды передаются на мембрану 12 , создавая периодические перепады давления в гидравлическом контуре 8 . Через гибкие шланги 14 давление передается в расширительные объемы 5 ячейки, вызывая вертикальные колебания двуслойной жидкой системы вдоль внутренних стенок ячейки. Для предотвращения смешивания жидкостей в контуре и ячейке используются разделительные мембраны 15 .

Процедура подготовки и проведения эксперимента включала несколько последовательных этапов. Сначала силиконовый вкладыш устанавливался между орг-стеклянных рамок, после чего вся конструкция фиксировалась двумя внешними алюминиевыми рамами 16 с помощью болтовых соединений, обеспечивающих герметичность рабочей полости. Затем в собранной ячейке формировалась двуслойная система смешивающихся жидкостей, описанных ниже в этом разделе. Далее через программное обеспечение CME 2 задавались частота f и амплитуда колебаний штока двигателя. В момент, когда двуслойной система была создана, осуществлялось перекрытие боковых подводящих трубок, после чего синхронно запускались колебания системы и видеосъемка эксперимента. Этот момент принимался за начало эксперимента t 0 . Видеозапись производилась цифровой камерой Fujifilm X-E 4 с частотой 60 кадров/с. Для обеспечения равномерного освещения использовался коллимированный источник рассеянного света ( Metaphase Technologies ), который располагался с тыльной стороны экспериментальной ячейки. Размер освещаемой области был меньше области захвата

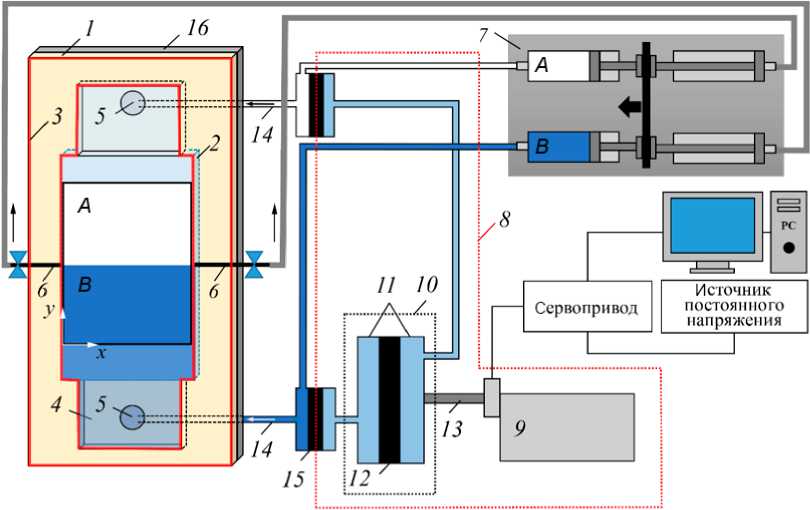
Рис. 1. Схематическое изображение экспериментальной установки. Расшифровка обозначений элементов установки приведена в тексте

камеры и составлял 8×6 см2 (В×Ш). Границы и расположение освещенной зоны показаны на рис. 1 черной рамкой.

В качестве рабочих жидкостей использовался более плотный водный раствор хлорида натрия ( NaCl , раствор B на рис. 1) с концентрацией 1 моль/л и коэффициентом диффузии D NaCl ≈ 1,5∙10^-5 см²/с, а также менее плотный водный раствор сахарозы ( C 12 H 22 O 11 , раствор А на рис. 1) с концентрацией 0,256 моль/л и коэффициентом диффузии D сахароза ≈ 0,5∙10^-5 см²/с. После формирования двуслойной системы между растворами начинается взаимная диффузия. Быстро диффундирующая соль перемещается вверх через диффузионную границу, локально увеличивая плотность. При этом медленная диффузия сахарозы, направленная сверху-вниз не компенсирует снижения концентрации соли, что приводит к локальному уменьшению плотности ниже диффузионной зоны. Таким образом, различие в коэффициентах молекулярной диффузии растворенных компонентов приводит к формированию на профиле плотности, характеризующего двуслойную систему, локальных областей с инверсной стратификацией, что в поле тяжести обуславливает развитие конвекции двойной диффузии.

Для визуализации динамики конвекции двойной диффузии и процесса взаимного смешения жидкостей в нижний (солевой) раствор был добавлен водорастворимый пищевой краситель c массовой концентраций 0,027 %. В настоящих экспериментах перенос вещества преимущественно определяется конвективным механизмом, а не молекулярной диффузией, поэтому краситель выступает в роли пассивного трассера, отражающего движение жидкости и общее распределение концентрации соли. Исследования проводились в следующем диапазоне частоты f = (2–4) Гц и амплитуды b = (0–0,66) см колебаний жидкой системы. Частота колебаний жидкости f совпадала с частотой двигателя. Однако амплитуда колебаний жидкой системы B отличалась от амплитуды двигателя вследствие гидродинамического сопротивления, инерции жидкости и упругих деформаций элементов установки. Фактическая амплитуда жидкой системы определялась по максимальному вертикальному смещению верхней точки всплывающей пальчиковой структуры за один период колебаний. Измеренное смещение соответствует удвоенной амплитуде колебаний жидкости.

Результаты

Структура конвекции

После начала эксперимента процесс взаимной диффузии между слоями сопровождается перестройкой вертикального профиля плотности. В результате в двуслойной системе на исходной границе между слоями формируется пальчиковая структура, распространяющаяся вверх и вниз. Серия изображений, демонстрирующая эволюцию двуслойной системы «соль – сахар» в условиях поршневых колебаний при частоте f = 3 Гц и амплитуде b = 0,32 Гц представлена на рис. 2.

Особенностью конвекции двойной диффузии является взаимопроникающий характер движения пальчиковой структуры, что способствует активному перемешиванию исходных растворов. В системе «соль – сахар» наблюдается незначительная асимметрия в скоростях восходящих и нисходящих пальцев, что уже ранее отмечалось в [35] и объясняется наличием

Рис. 2. Серия изображений, демонстрирующая эволюцию пальчиковой структуры конвекции двойной диффузии в условиях поршневых колебаний жидкости при частоте f = 3 Гц и амплитуде b = 0,32 Гц. Время с момента начала эксперимента t , c: 1, 59, 88, 117 (слева направо соответственно). Красной горизонтальной линией обозначено положение верхней границы диффузионной зоны x d . Синей линией обозначено горизонтальное сечение, вдоль которого извлекались профили яркости I ( x ), используемые для построения пространственно-временных карт. Ширина каждого изображения 6 см. Черной рамкой ограничена область, анализируемая при оценке степени взаимного смешения исходных слоев

зависимости коэффициентов диффузии от концентрации растворенных веществ [36]. Отметим, что для большинства неорганических соединений концентрационная зависимость диффузии слабая. Поэтому при использовании в эксперименте растворов веществ, скорость диффузии которых не зависит (или слабо зависит) от концентрации, скорость распространения нижних и верхних пальцев будет одинаковой.

Для анализа нелинейной динамики и структуры конвекции двойной диффузии в условиях действия поршневых колебаний и при их отсутствии использовались пространственно-временные карты. Карты позволяют визуализировать формирование, развитие, и взаимодействие пальчиковых структур в ходе эксперимента. Построение карт осуществлялось следующим образом. Серия кадров, экспортированных из видеозаписи эксперимента длительностью 120 с, преобразовывалась в числовые матрицы яркости I(x, y) в градациях серого. Экспортированные кадры соответствовали одной и той же фазе колебаний. Из каждой матрицы извлекался одномерный массив значений яркости I(x), соответствующий горизонтальному срезу (синяя линия на рис. 2), проходящему вблизи верхней границы диффузионной зоны (красная линия на рис. 2). В стационарных случаях, когда область генерации структур остается с течением времени фиксированной в пространстве, срез, для которого извлекается профиль яркости, выбирают на постоянном расстоянии от этой области. Однако в рассматриваемом эксперименте вследствие диффузии и развивающейся конвекции вертикальный размер диффузионной зоны между слоями со временем увеличивается. В результате зона, в которой пальчиковые структуры становятся визуально различимыми, смещается. Для учета этого смещения профили яркости I(x) извлекались вдоль динамически перемещающейся линии, расположенной на фиксированном расстоянии 0,2 см выше положения верхней границы диффузионной зоны xd. Положение границы xd для каждого кадра определялось по максимуму производной вертикального профиля средней яркости dI / dy , который был получен в результате усреднения яркости по ширине изображения. Последовательность профилей яркости I(x) объединялась в двумерную пространственно-временную карту. Ввиду того, что профили яркости извлекались из центральной части кадра, где влияние виньетирования пренебрежимо мало, предварительная коррекция неравномерности освещения анализируемых изображений не требовалась. Для обеспечения корректного сравнения результатов, полученных для различных экспериментальных реализаций, значения интенсивности I(x) нормировались на максимальное значение Imax. Полученные карты представлены на рис. 3.

В отсутствие поршневых колебаний (рис. 3, а ) наблюдается классическое развитие пальчиковых структур, характерных для конвекции двойной диффузии. На начальном этапе формируется квазирегулярная мелкомасштабная пальчиковая структура, которая движется преимущественно в вертикальном направлении с незначительной горизонтальной составляющей скорости. После образования первичных пальцев происходит их непрерывная генерация в течение всего процесса смешения, пока система не достигнет однородного состояния. Этот процесс обусловлен сохранением градиентов концентрации между компонентами с различными коэффициентами диффузии, это создает области с неустойчивым распределением плотности, что в поле тяжести приводит к развитию конвективной неустойчивости. По мере эволюции системы отдельные пальцы объединяются, что соответствует началу нелинейного режима конвекции. Коалесценция пальцев приводит к монотонному увеличению характерной длины волны пальцев со временем, что отчетливо видно на пространственно-временных картах.

При включении поршневых колебаний динамика

Рис. 3. Пространственно-временные карты, характеризующие эволюцию структуры конвекции двойной диффузии.

Пунктирными линиями на рис. 3, a обозначены срезы, для которых проводилось измерение длины волны. Срезы соответствуют моментам времени 30, 60 и 90 с (сверху вниз соответственно)

системы существенно изменяется. Рассмотрим серию пространственно-временных карт, полученную для частоты f = 3 Гц (см. рис. 3, д – з ). Установлено, что увеличение амплитуды колебаний приводит к тому, что пальчиковая структура становится более регулярной и приобретает более выраженную вертикальную ориентацию. Это объясняется увеличением доминирующего влияния инерционных сил, которые способствуют выравниванию концентрационных градиентов и подавлению случайных флуктуаций [13], что приводит к стабилизации и регуляризации пальчиковой структуры. Кроме того, с ростом амплитуды наблюдается уменьшение пространственной устойчивости пальцев: как первичные, так и вторичные структуры становятся размытыми. Этот эффект обусловлен дисперсией Тейлора [37] – явлением, при котором осциллирующие сдвиговые потоки, взаимодействуя с молекулярной диффузией, приводят к эффективному увеличению продольного переноса вещества, ускоренному диффузионному размытию структур и интенсификации процесса коалесценции пальцев.

При амплитудах b ≥ 0,45 см вблизи боковых стенок ячейки наблюдаются краевые эффекты, связанные с вязким торможением колебательного движения жидкости в пограничных слоях. Вблизи границ ячейки амплитуда колебаний экспоненциально затухает, что приводит к усилению градиентов скорости, что, в свою очередь, ускоряет коалесценцию пальцев, приводя к росту характерной длины волны.

Время зарождения конвективных структур не зависит от присутствия колебаний и составляет в среднем

15 с. Это указывает на то, что начальная стадия развития неустойчивости определяется исключительно диффузионными процессами.

Сравнительный анализ пространственно-временных карт, полученных для различных частот при близкой амплитуде (см. рис. 3, г , д ) не выявил значимых различий. По-видимому, для выявления зависимости структуры конвекции двойной диффузии от частоты необходимо провести дополнительные исследования в более широком частотном диапазоне.

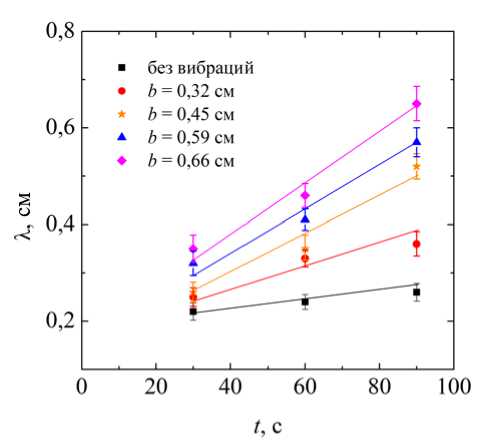
Для количественной оценки пространственного распределения пальчиковых структур была проанализирована их длина волны λ в экспериментах с частотой колебаний f = 3 Гц и в отсутствие поршневых колебаний. Оценка длины волны выполнена для трех горизонтальных срезов пространственно-временных карт, соответствующих начальной ( t = 30 с), средней ( t = 60 с) и финальной ( t = 90 с) стадиям развития конвекции. В каждом срезе определялось среднее количество пальцев, по которому вычислялась длина волны. На рис. 4, а , б, представлены зависимости длины волны от времени и амплитуды колебаний жидкой системы соответственно. Хорошо видно, что длина волны увеличивается со временем как в случае колебаний, так и в их отсутствие, отражая процесс объединения пальчиковых структур. При этом в присутствии поршневых колебаний темп роста длины волны значительно выше, что свидетельствует об усилении неустойчивости и взаимодействия между пальчиковыми структурами.

а

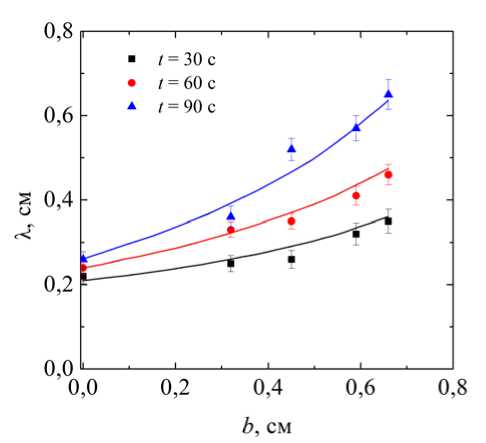
Рис. 4. а - временная зависимость длины волны пальчиковой структуры; б - зависимость длины волны пальчиковой структуры от амплитуды поршневых колебаний

б

Все зависимости Х( t ) описываются линейным законом Х( t )=Zo + S г t . Полученные угловые коэффициенты S x показывают, что скорость увеличения длины волны монотонно возрастает с увеличением амплитуды вибраций: от 9-10^-4 (без вибраций) до 540^-3 см/с (при b = 0,66 см).

Интенсификация массопереноса

На пространственно-временных картах (см. рис. 3) видно, что конвективные пальцы в случае с поршневыми колебаниями обладают большей цветовой насыщенностью по сравнению со случаем без колебаний, что качественно подтверждает более эффективный процесс переноса вещества в случае с колебаниями. Этот эффект не связан с различием в графической обработке изображений или условиях освещения, а имеет физическую природу. Вибрации индуцируют дополнительное перемешивание и усиление продольного массопереноса, аналогично эффекту дисперсии Тейлора, что обусловливает увеличение концентрации красителя и растворенных компонентов внутри пальчиковых структур. Аналогичные эффекты усиленного переноса вещества под действием осциллирующих потоков были рассмотрены в [38; 39].

Для количественной оценки степени смешения растворов был использован параметр смешения M [40]. Расчет параметра смешения основан на анализе изменения стандартного отклонения цвета σ в градациях серого. Значение M для момента времени t i вычислялось следующим образом:

M = 1 -

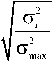
где g i - стандартное отклонение в момент времени t i , а о max — стандартное отклонение в начальный момент времени 1 ₀ Значение параметра M = 1 соответствует полному смешению слоев (100 %), а значение M = 0 указывает на полное разделение слоев (0 %).

Расчет параметра M выполнялся по следующему алгоритму. На первом этапе из видеозаписи эксперимента экспортировалась серия кадров в градациях серого, синхронизированных по фазе колебаний. Для компенсации пространственной неоднородности освещения применялась процедура вычитания фонового изображения, полученного при равномерной подсветке пустой ячейки до начала эксперимента. Данное фоновое изображение содержало информацию о неоднородностях освещения, обусловленных неравномерностью распределения светового потока, а также аберраций, вызванных оптической системой визуализации. Несмотря на процедуру коррекции, на изображениях по-прежнему наблюдались остаточные пространственные вариации освещенности. Для их исключения выполнялось кадрирование изображений до области анализа размером 6,30^х5,35 см² (В^ХШ), границы которой обозначены черной рамкой на рис. 2. Далее каждое изображение преобразовывалось в двумерную матрицу значений яркости I ( x , у ). Предполагая, что процесс смешения в ячейке однороден вдоль горизонтальной оси x , проводилось усреднение значений яркости по строкам матрицы, что соответствует усреднению по ширине ячейки. Таким образом, формировался одномерный массив, отражающий вертикальный профиль интенсивности изображения I(у ). Согласно закону Ламберта - Бера, интенсивность прошедшего света линейно связана с концентрацией поглощающего вещества. Следовательно, полученный вертикальный профиль яркости может быть интерпретирован как профиль распределения

0.0 02 0.4 0.6 0,8 b, см

0.20

0,15

0,10

0.05

0,00

20   40   60   80   100   120

б

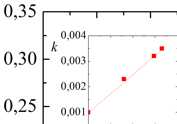
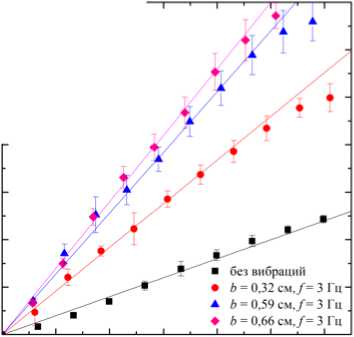
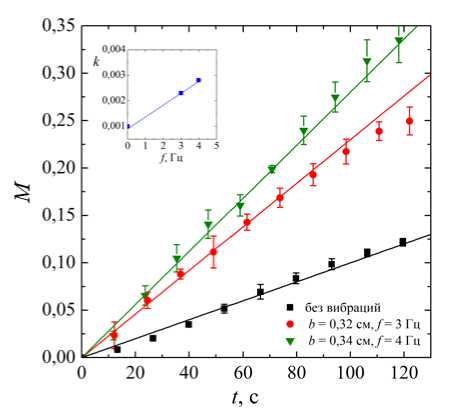
Рис. 5. Временные зависимости параметра смешения M ( t ) при а - фиксированной частоте f = 3 Гц;

б - близкой амплитуде поршневых колебаний. Сплошные линии соответствуют линейной аппроксимации экспериментальных данных. На вставках представлены зависимости угла наклона k = dM / dt аппроксимирующих прямых от параметров поршневых колебаний

а

концентрации красителя вдоль вертикальной координаты [41]. Далее для каждого кадра вычислялось стандартное отклонение σ вертикального профиля яркости, на основании которого рассчитывался безразмерный параметр M , характеризующий степень взаимного смешения растворов.

На рис. 5 представлены временные зависимости параметра смешения M , полученные при фиксированной частоте f = 3 Гц (рис. 5, а ) и близкой амплитуде b = 0,32-0,34 см (рис. 5, б). Хорошо видно, что включение поршневых колебаний значительно интенсифицирует процесс смешения по сравнению со случаем без колебаний. На начальном этапе все зависимости M ( t ) носят линейный характер, что позволяет охарактеризовать скорость массопереноса по углу наклона k = dM / dt аппроксимирующих прямых (сплошные линии на рис. 5). Полученные зависимости скорости массопере-носа k от амплитуды и частоты колебаний (см. вставки на рис. 5) монотонно возрастают, что указывает на включение дополнительных механизмов переноса, индуцируемых вибрациями. При этом влияние амплитуды выражено сильнее, о чем свидетельствует более крутой наклон зависимости k ( b ) по сравнению с k ( f ). Полученные результаты подтверждают, что взаимодействие осциллирующих потоков с молекулярной диффузией усиливает продольный перенос и разрушает стратификацию жидкости, ускоряя гомогенизацию системы. Это согласуется с гипотезой о включении вибрационно-индуцированного механизма, аналогичного дисперсии Тейлора.

Обсуждение

Для описания процессов переноса в исследуемой системе необходимо учитывать совокупное действие нескольких механизмов: молекулярной диффузии, конвекции двойной диффузии, а также вибрационно-индуцированных течений. Их взаимодействие приводит к ускоренному размытию начальной диффузионной зоны между исходными слоями и интенсивной гомогенизации жидкой системы, что можно интерпретировать как эффективный диффузионный перенос. В качестве дополнительной количественной характеристики процесса смешения рассчитан эффективный коэффициент диффузии Def, отражающий интегральную скорость перемешивания исходных растворов. Оценка Deff проводилась на основе аппроксимации экспериментальных зависимостей M(t) экспоненциальной моделью выравнивания концентрации:

M (t) = 1 — exp I — - I,, l т)

где т - характерное время установления стационарного профиля концентрации в двуслойной системе. Этот подход основан на решении одномерного уравнения диффузии в ограниченной области и позволяет связать параметр τ с эффективным коэффициентом диффузии через выражение:

D f =I?

п т

где L - характерная длина системы, в качестве которой выбрана высота области, используемой для анализа процесса смешения ( L = 6,3 см). Это обеспечивает согласованность между пространственным масштабом, по которому рассчитывается скорость выравнивания концентрации, и масштабом, используемым для количественной оценки эффективности переноса вещества.

Хотя исследуемая система является многокомпонентной, расчет параметра M осуществлялся по оптическому контрасту, обусловленному концентрацией только одного компонента (красителя), который является пассивным индикатором процессов переноса. Поэтому можно полагать, что усредненное распределение красителя отражает совокупное влияние всех механизмов переноса (двойная диффузия и вибрационно-индуцированные потоки). Поэтому использование упрощенной одномерной модели (2) для первичной оценки эффективности переноса допустимо.

Определение характерного времени диффузии τ проводилось на основе анализа экспериментальных зависимостей M ( t ) (см. рис. 5). Исходная модель (2) была линеаризована путем логарифмического преобразования:

ln[1 - M ( t )] = - 1 / т . (4)

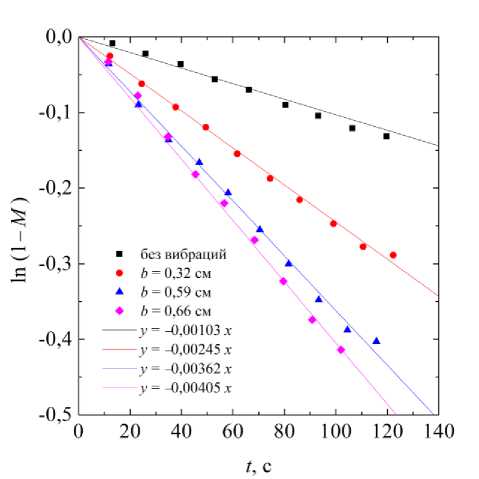
Полученные зависимости ln[1 - M ( t )] от времени t для различных амплитуд колебаний при фиксированной частоте f = 3 Гц представлены на рис. 6, а . Сплошные линии соответствуют линейным аппроксимациям вида ln(1– M ) = α· t . Хорошо видно, что аппроксимирующие прямые демонстрируют хорошее соответствие с экспериментальными данными, что подтверждает применимость выбранной экспоненциальной модели (2) для описания исследуемого процесса смешения.

Значения τ определялись через угловые коэффициенты аппроксимирующих прямых следующим образом: τ = –1/α. На основании полученных значений τ были рассчитаны значения эффективного коэффициента диффузии Deff согласно выражению (3) для различных амплитуд колебаний при фиксированной частоте (f = 3 Гц). Значения угловых коэффициентов α аппроксимирующих прямых, значения характерного времени τ и коэффициенты эффективной диффузии Deff представлены в таблице. Полученная зависимость эффективного коэффициента диффузии от амплитуды поршневых колебаний при фиксированной частоте f = 3 Гц представлена на рис. 6, б. Анализ показал, что эффективный коэффициент диффузии линейно увеличивается с ростом амплитуды поршневых колебаний, что однозначно подтверждает существенный вклад вибрационно-индуцированных потоков в интенсификацию массопе-реноса. Характерно, что уже при относительно малой амплитуде (b = 0,32 см) наблюдается двукратное увеличение Deff, что указывает на высокую чувствительность системы к вибрационному воздействию. В исследуемом диапазоне амплитуд максимальный прирост эффективной диффузии достигал почти четырехкратного значения (при амплитуде b = 0,66 см). Полученные результаты подтверждают перспективность использования управляемых поршневых колебаний для контроля мас-сопереноса в стратифицированных жидких системах, включая системы апвеллинга и другие геофизические и инженерные системы.

Заключение

В настоящей статье представлены результаты экспериментального исследования влияния вертикальных поршневых колебаний на динамику конвекции двойной диффузии и интенсификацию массообменных процессов в двуслойной системе смешивающихся жидкостей в вертикальной ячейке Хеле-Шоу. Показано, что поршневые колебания с частотой 2–4 Гц и амплитудой до 0,66 см приводят к существенным изменениям в структуре конвективных течений и эффективности перемешивания.

а

Рис. 6. а – логарифмическая зависимость параметра смешения М от времени для различных амплитуд колебаний; б – зависимость эффективного коэффициента диффузии от амплитуды колебаний при фиксированной частоте f = 3 Гц

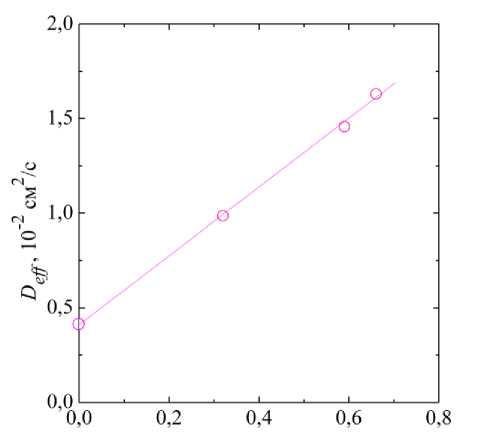
b, cm б

Параметры экспоненциального выравнивания концентрации, определенные на основе линейной аппроксимации логарифмической зависимости ln[1- M] ( t ): значения угловых коэффициентов а, характерного времени т и эффективного коэффициента диффузии D eff при различных амплитудах поршневых колебаний

Параметры колебаний	а , с-1	т = -1/а , с	D eff , 10 2 см2/с
b = 0, f = 0 Гц	–0,00103	970,87	0,41
b = 0,32 см, f = 3 Гц	–0,00245	408,16	0,99
b = 0,59 см, f = 3 Гц	–0,00362	276,24	1,45
b = 0,66 см, f = 3 Гц	–0,00405	246,91	1,63

Пространственно-временной анализ показал, что с увеличением амплитуды колебаний при фиксированной частоте 3 Гц пальчиковые структуры становятся более регулярными, приобретают выраженную вертикальную ориентацию и демонстрируют ускоренную коалесценцию. При амплитудах b ≥ 0,45 см выявлены вторичные эффекты, выражающиеся в потере пространственной устойчивости пальчиковой структуры и ускоренном размытии диффузионной зоны между исходными слоями, что обусловлено интенсификацией продольного массопереноса.

Для количественной оценки степени взаимного смешения слоев использовался безразмерный параметр смешения M , который рассчитывался на основе анализа стандартного отклонения яркости изображений в градациях серого, отражающий распределение концентрации красителя. Полученные зависимости M ( t ) продемонстрировали значительное увеличение степени гомогенизации при наличии поршневых колебаний. Линейная аппроксимация зависимостей M ( t ) позволила определить скорость массопереноса по углу наклона аппроксимирующих       прямых        k = d M/ d t .

Показано,     что     скорость     массопереноса