Экспериментальные исследования и идентификация модели динамической системы «виброзащитное кресло - оператор» мобильной машины

В настоящее время при создании транспортных и технологических машин различного назначения важным является обеспечение комфортных условий и выполнение санитарных норм на рабочем месте водителя-оператора. Для промышленных гусеничных тракторов особенно важной является задача защиты от вибраций, поступающих от гусеничного движителя, двигателя и технологического оборудования. Превышение допустимого уровня вибраций приводит к повышенной утомляемости водителя, а также к заболеваниям позвоночника и вибрационной болезни [1]. Снизить уровень вибраций до приемлемого уровня в источнике или за счет виброизоляции кабины удается далеко не всегда, поэтому в качестве элементов защиты оператора широко применяются виброзащитные сиденья различной конструкции.

Для выбора оптимальных параметров сиденья при проектировании машины применяется математическое моделирование. Для получения наиболее точных результатов необходимо использовать математическую модель, описывающую динамику системы «виброзащитное кресло – тело оператора». В настоящее время при расчетах часто используют упрощенные модели, где тело оператора заменяется сосредоточенной массой. Повысить точность результатов исследований можно при использовании более сложных моделей. При этом также появится возможность исследовать колебания различных частей тела водителя-оператора и использовать новые критерии вибрационной нагруженности, например, энергию, поглощаемую телом [2, 3]. Важность учета динамических процессов в колеблющемся теле оператора косвенно подтверждается нормативными документами (например, [4]), предусматривающими проведение стендовых испытаний виброзащитных сидений вместе с находящимся на них человеком. В настоящее время разработан ряд математических моделей, описывающий колебания тела водителя-оператора. Однако при этом модели, предлагаемые различными исследователями, имеют разную структуру и каждая из них соответствует оператору с какой-либо одной массой тела. В связи с этим актуальной является задача разработки математической модели системы «виброзащитное кресло – тело водителя-оператора» и определение набора ее параметров, соответствующих операторам с различной массой тела.

Виброзащитные сиденья по конструкции можно разделить на две большие группы – с пассивной и активной системами подрессоривания. Сиденья первого типа наиболее распространены, их конструкция обычно включает упругий и демпфирующий элементы в системе подрессорива-ния, а также мягкую подушку. В качестве упругого элемента могут использоваться пружины, торсионы, пневматические рессоры. Конструкция сиденья обычно предусматривает регулировку по росту и массе водителя.

Сиденья с активным подрессориванием могут включать управляемые упругие элементы или амотризаторы, характеристика которых изменяется при колебаниях сиденья [5], исполнительные механизмы, задающие силовое воздействие на подвижную часть сиденья в противофазе с внешним воздействием [6–8] и др. Управление активными элементами осуществляется специальным контроллером по сигналам датчиков-акселерометров таким образом, чтобы минимизировать колебания подушки сиденья, на которой располагается оператор. Такие сиденья обеспечивают наиболее эффективное снижение вибраций, однако они дороги, имеют сложную конструкцию, в связи с этим потенциально менее надежны и пока не находят широкого применения.

Статья посвящена разработке математической модели системы «виброзащитное сиденье – оператор» промышленного трактора. При этом рассматривается виброзащитное сиденье фирмы Sibeco с пассивной системой подрессоривания, включающее пневматический упругий элемент. Исследованию характеристик таких сидений посвящены работы [9–12]. Получены характеристики упругого и демпфирующего элементов системы подрессоривания, соответствующие различным настройкам сиденья по массе водителя. В работах [12, 13] исследованы характеристики подушки сиденья и их влияние на подавление вибраций.

При описании динамики тела оператора, находящегося на виброзащитном сиденье, используются различные модели. В наиболее простом случае оператор моделируется одной сосредоточенной массой. Однако полученные при этом результаты зачастую отличаются от экспериментальных данных, полученных при стендовых и натурных испытаниях сиденья с оператором. В связи с этим необходимо использовать более сложные модели.

В ряде работ для описания динамики тела оператора используется конечноэлементная модель [3]. При этом модель может быть весьма подробной. Однако при ее разработке могут возникнуть трудности с определением свойств материалов, моделирующих тело человека, а проведение расчетов занимает большое время. В связи с отмеченным большое распространение получили модели, в которых тело человека описывается набором сосредоточенных масс, а также упругих и демпфирующих элементов. В настоящее время предложен ряд подобных моделей различной сложности, описывающих вертикальные колебания тела сидящего человека.

В наиболее простых моделях, использовавшихся в ранних исследованиях, тело человека по вертикали условно разделяется на две или три части и, соответственно, описывается двух- или трехмасcовыми расчетными схемами [14, 15]. Трехмассовая модель также представлена в стандарте ISO 5982 [16]. В настоящее время большее распространение получили модели, описывающие колебания нижней и верхней частей туловища, головы и внутренних органов. Расчетные схемы таких моделей, описывающих вертикальные колебания, представлены на рис. 1. Входное воздействие для представленных моделей – это вертикальное перемещение кресла; обобщенными координатами являются вертикальные перемещения масс.

Расчетная схема (рис. 1, a) включает нижнюю часть туловища (m₂), верхнюю часть ( m ₄), голову ( m ₅) и внутренние органы( m ₃) В работе [2] приведены параметры этой модели для человека массой 60,7 кг.

Схема (рис. 1, b) отличается отсутствием упругого и демпфирующего элементов ( c 6 и b 6 ). В [17] приведены параметры этой модели для человека массой 76 кг, в [2] – для человека массой 55,2 кг.

В модели (рис. 1, c) внутренние органы описываются двумя массами ( m ₃ и m ₆). В [18] представлены ее параметры для человека массой 72 кг.

Модель (рис. 1, d) описывает внутренние органы тремя массами ( m ₃, m ₃₁ и m ₃₂). Верхняя часть туловища также разделена на две массы ( m 4 и m 41 ) [19].

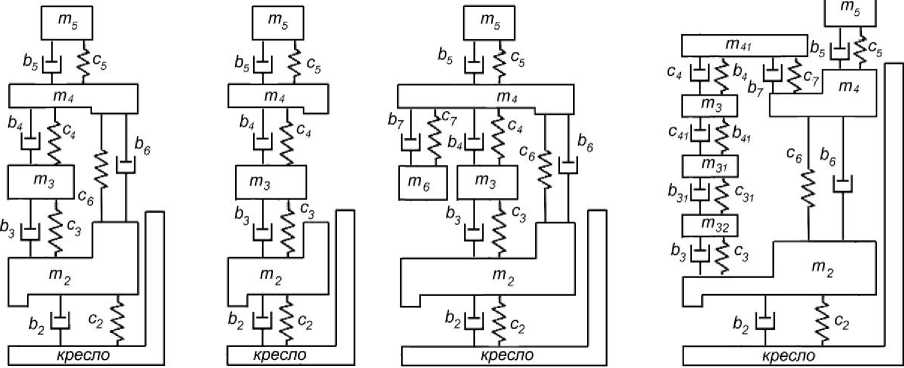
a)                             b)                               c)                                          d)

Рис. 1. Расчетные схемы математических моделей сидящего человека Fig. 1. Calculation schemes for mathematical models of a sitting person

Параметры перечисленных моделей представлены в табл. 1. Анализ этих данных показывает, что параметры моделей, приводимые в работах разных авторов, существенно различаются даже при описании людей с близкой массой тела.

Представленное в статье исследование посвящено разработке математической модели, описывающей вертикальные колебания динамической системы «виброзащитное сиденье – человек-оператор». Для определения параметров модели использованы результаты испытаний на вибростенде сиденья с людьми различной массы. В статье приводится описание экспериментальной установки и методики проведения испытаний. Представлены параметры модели для операторов с различной массой тела.

Таблица 1 Параметры математических моделей сидящего человека

Table 1

Parameters of mathematical models of a sitting person

Параметры модели	Масса оператора; расчетная схема модели (рис. 1)
	55,2 кг; схема b	60,1 кг; схема a	72 кг; схема c	76 кг; схема b	81 кг; схема d
m 2 , кг	12,80	360	10,20	18	27
m 3 , кг	8,60	5,50	9,0	12,2	1,4
m 31 , кг	–	–	–	–	0,46
m 32 , кг	–	–	–	–	6,02
m 4 , кг	28,5	15	20,2	40,3	6,94
m41, кг	–	–	28	–	33,3
m 5 , кг	5,31	4,17	5,8	5,5	5,6
m 6 , кг	–	–	8,1	–	6,02

Окончание табл. 1

Table 1 (end)

Параметры модели	Масса оператора; расчетная схема модели (рис. 1)
	55,2 кг; схема b	60,1 кг; схема a	72 кг; схема c	76 кг; схема b	81 кг; схема d
c2, Н/м	90000	49340	120100	21670	25500
c 3 , Н/м	162800	20000	5300	17200	8940
c 31 , Н/м	—	—	—	—	8940
c4, Н/м	18300	10000	9150	309600	8940
c 41 , Н/м	—	—	—	—	8940
c 5 , Н/м	310000	134400	292000	5900	53640
c6, Н/м	–	–	128200	–	53640
c 7 , Н /м	—	—	13172	—	53640
b 2 , Н ⋅ c/м	2060	2480	2375	500	378
b 3 , Н ⋅ c/м	4580	330	677	1920	298
b 31 , Н ⋅ c/м	–	–	–	–	298
b 4 , Н ⋅ c/м	4750	200	1792	232	298
b 41 , Н ⋅ c/м	–	–	–	–	298
b 5 , Н ⋅ c /м	400	250	979	95	3651
b 6 , Н ⋅ c/м	–	909	4020	–	3651
b 7 , Н ⋅ c/м	–	–	144	–	3651

Материалы и методы

Экспериментальные исследования динамики системы «виброзащитное сиденье – человек-оператор» проводились в Центре виброиспытаний и мониторинга состояния конструкций ЮжноУральского государственного университета. Экспериментальная установка включала следующую аппаратуру (рис. 2):

– электродинамический вибростенд LDS V850. Вибростенд имеет допустимую нагрузку на вибростол до 350 кг, обеспечивает толкающее усилие до 22 кН, частотный диапазон до 3 кГц и амплитуду виброускорений до 60g (при синусоидальной вибрации);

– систему управления для вибрационных испытаний Bruel&Kjaer VC-LAN 7542. В качестве датчика обратной связи используется пьезоэлектрический акселерометр PCB 352C04, установленный на подвижный стол вибростенда;

– акселерометры PCB 333B30, закрепленные на элементах виброзащитного сиденья и на теле оператора;

– управляющий персональный компьютер.

На подвижной платформе вибростенда установлены акселерометры обратной связи системы управления (Ду) и системы сбора данных (Дк). Акселерометр Д1 установлен на верхней платформе кресла под верхней подушкой. Акселерометр Д2 закреплен на специальном податливом диске, используемом в соответствии с ГОСТ [4] при виброиспытаниях сидений. Он находится на подушке сиденья под человеком-испытателем.

При размещении акселерометров непосредственно на испытателе необходимо обеспечить их неподвижность относительно тела. В связи с этим акселерометр Д4 был установлен на податливую пластиковую пластину, которая плотно привязывалась к груди испытателя. Акселерометр Д5 устанавливался на каске, которая плотно надевалась на голову. На рис. 3 представлена фотография установленного на стенд виброзащитного сиденья с испытателем.

Испытания проводились с участием группы добровольцев, имевших массу тела от 52 до 118 кг. В процессе испытаний использовалось гармоническое нагружение с постоянной амплитудой виброускорений и плавно изменяющейся частотой от 2 до 10 Гц. После обработки результатов были получены частотные передаточные функции, отображающие реакции различных эле- ментов динамической системы на единичное гармоническое воздействие со стороны нижней платформы сиденья, закрепленной на столе вибростенда. С каждым из испытателей эксперимент повторялся по три раза, результаты осреднялись.

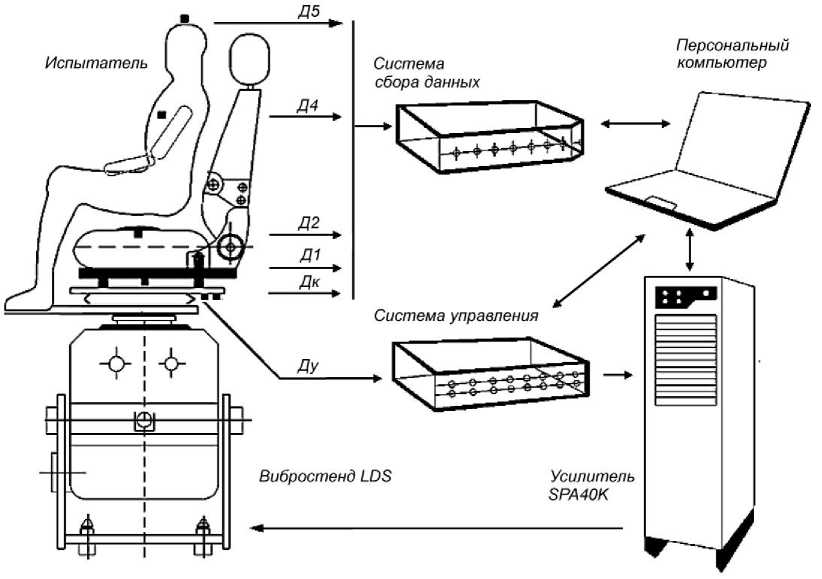
Рис. 2. Схема экспериментальной установки Fig. 2. Scheme of equipment for the experiment

Расчетная схема предложенной в данном исследовании математической модели приведена на рис. 4. Элементы m 1 , c 1 , b , b 1 , c 2 и b 2 описывают виброзащитное кресло. Масса m 1 соответствует верхней части сиденья, установленной на системе подрессоривания; для данного сиденья она равна 20 кг. Элементы c 1 , b , b 1 описывают систему подрессоривания. Последовательнопараллельная схема была обоснована в ходе ранее проведенных исследований. Следует отметить, что такая модель пригодна только для описания колебаний системы без учета постоянной составляющей нагрузки. Элементы c 2 , b 2 описывают подушку кресла. Параметры этих элементов для настроек кресла, соответствующих различной массе человека-оператора, приведены в [12].

Остальные элементы (массы m 2 – m 5 , упругие и демпфирующие элементы c 2 – c 6 , b 2 – b 6 ) соответствуют модели тела человека (см. рис. 1, а). Их значения для операторов различной массы предварительно были определены на основе анализа литературных данных. Входным кинематическим воздействием для модели является вертикальное перемещение основания x(t) , обобщенными координатами – вертикальные перемещения масс ( y ₁ – y ₆). Также введена дополнительная координата y 0 , соответствующая вертикальному перемещению точки соединения элементов c 1 и b . Динамика представленной математической модели описывается следующей системой дифференциальных уравнений:

b(yo -,У1) = ci(x-Уо), m1y1 = b(У0 - У1) + b1(x - y1) + c2(У2 - У1) + b2(y2 - yl), m2y2 = c2(У1 -У2) + b2(y1 -y2) + c3(У3 -У2) + b3(y3 -y2) + c6(У4 -У2) + b6(y4 -y2), m3У3 = c3(У2 -У3) + b3(У2 -У3) + c4(У4 -У3) + b4(У4 -У3), m4J>4 = c4(У3 -У4) + b4(У3 -У4) + c5(У5 -У4) + b5(У5 -У4) + c6(У2 -У4) + b6(У2 -У4), m5У5 = c5(У4 -У5) + b5(У4 -У5)•

Рис. 3. Испытатель на виброзащитном сиденье на вибростенде Fig. 3. Tester in a anti-vibration seat on a electrodynamic vibration bench

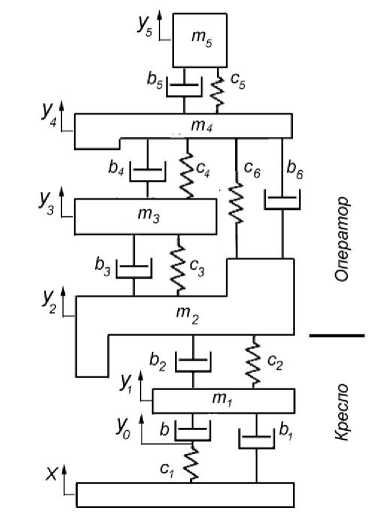
Рис. 4. Расчетная схема модели виброзащитного сиденья с оператором

Fig. 4. Calculation scheme of a model of a anti-vibration seat with an operator

После преобразований [20] из этих уравнений были получены выражения для частотных передаточных функций. В дальнейшем параметры элементов модели, описывающих тело человека, были уточнены для обеспечения наилучшего соответствия расчетных и экспериментальных данных.

Результаты и обсуждения

В качестве примера на рис. 5 представлены расчетные частотные передаточные функции для оператора с массой тела 73 кг. Там же приведены экспериментальные передаточные функции для координат y 1 , y 2 , y 4 , y 6 , полученные на основе сигналов акселерометров Дк, Д1, Д2, Д4 и Д5. Параметры модели для операторов с массой тела 52, 66, 73, 85 и 118 кг представлены в табл. 2.

В результате уточнения параметров элементов модели, описывающих тело оператора, удалось обеспечить достаточно хорошее соответствие расчетных и экспериментальных данных. Небольшие локальные всплески, присутствующие на экспериментальных передаточных функциях, по-видимому, вызваны резонансами отдельных элементов виброзащитного сиденья, не учитываемых в математической модели. Следует отметить существенное расхождение расчетной и экспериментальной передаточных функций для обобщенной координаты y 4 , соответствующей колебаниям верхней части тела оператора. По-видимому, это вызвано не вполне удачным размещением акселерометра Д4 (ближе к средней части туловища), а также недостаточно жесткой связью с телом испытателя.

Представленная в статье математическая модель будет использована в дальнейших исследованиях для получения расчетных оценок вибронагруженности рабочего места оператора промышленного гусеничного трактора. При этом могут быть проведены исследования для операторов с различной массой тела.

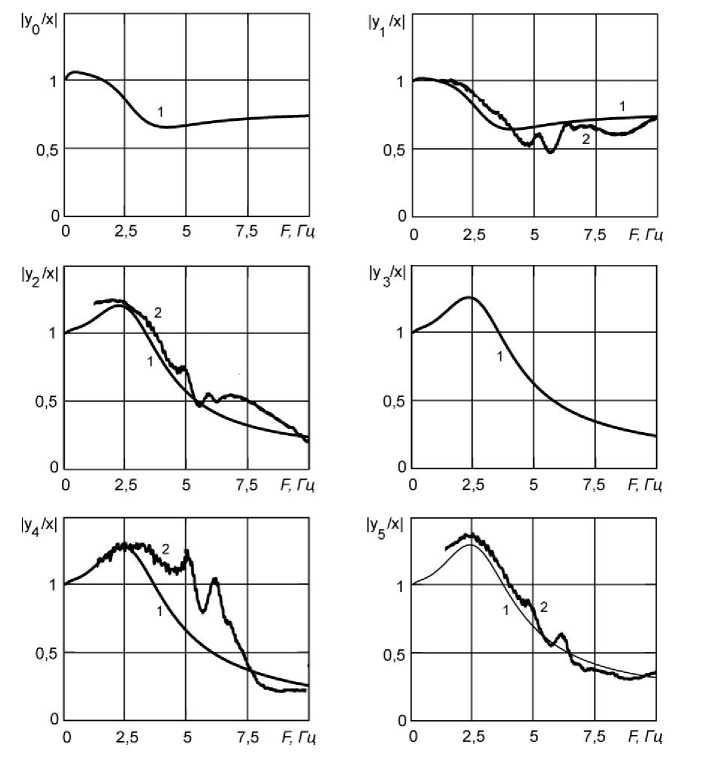
Рис. 5. Расчетные и экспериментальные передаточные функции для испытателя массой 73 кг;

1 – расчет, 2 – эксперимент

Fig. 5. Calculated and experimental transfer functions for a tester with a mass of 73 kg;

1 – calculation, 2 – experiment

Таблица 2

Параметры математической модели виброзащитного сиденья с оператором

Table 2

Parameters of the mathematical model of an anti-vibration seat with an operator

Параметры модели	Масса оператора, кг
	52	66	73	85	118
m1, кг	20	20	20	20	20
m 2 , кг	10,9	17,2	18,4	24,8	37
m3, кг	11,5	11,2	12,4	13,7	16,7
m4, кг	25	32,3	36,7	40,4	58
m 5 , кг	4,6	5,3	5,5	6,1	6,3
c 1 , Н/м	3100	3600	5218	5600	6070
c2, Н/м	170000	195000	220000	230000	290000
c 3 , Н/м	24320	18180	15100	9800	7600
c 4 , Н/м	15200	10200	9100	8700	6300
c5, Н/м	172360	111300	84410	52760	37820
c 6 , Н /м	254000	166000	122400	111700	80600
b, Н ⋅ c/м	1100	1800	2300	2800	3500
b1, Н ⋅ c/м	950	1100	3200	3700	4300
b 2 , Н ⋅ c/м	1100	1300	1500	16200	18100

Окончание табл. 2

Table 2 (end)

Параметры модели	Масса оператора, кг
	52	66	73	85	118
b 3 , Н ⋅ c/м	4940	3180	2300	1300	780
b 4 , Н ⋅ c/м	5270	2840	1620	790	220
b 5 , Н ⋅ c /м	400	220	120	110	76
b 6 , Н ⋅ c/м	4840	4267	3800	3400	2100