Экспериментальный лазерный кругломер, исследование основной погрешности измерений

В настоящее время в данной области техники для контроля поверхности используют в основном устройства на основе интерференцион-

ных методов [1, 2]. Контролируемая поверхность сложной формы вносит искажения во входной сигнал. Исправление данных искажений на уровне контролирующей аппаратуры является дорогостоящей задачей. Применяемый в настоящей работе метод триангуляции позволяет обойтись без дорогостоящей оптики и как следствие – сделать оборудование более доступным.

Данный метод является одной из разновидностей методов триангуляции, которая основана на использовании зеркальной составляющей отраженного пучка света (рис. 1). Ее иногда также называют дефлектометрией. Можно также найти ее некоторое идейное сходство с известными датчиками Шака-Гартмана [3]. Их чувствительность может достигать 5×10-4 мкм, что сравнимо с лучшими интерферометрами.

Данный метод представляет интерес для применения в различных задачах [4]. Это имеет место благодаря его большей чувствительностью по сравнению с наиболее распространенной разновидностью метода триангуляции. Она основана на анализе оптического изображения световой точки, или же световой структуры на контролируемой поверхности. Однако применение сдерживается отсутствием функции преобразования в каждом конкретном случае.

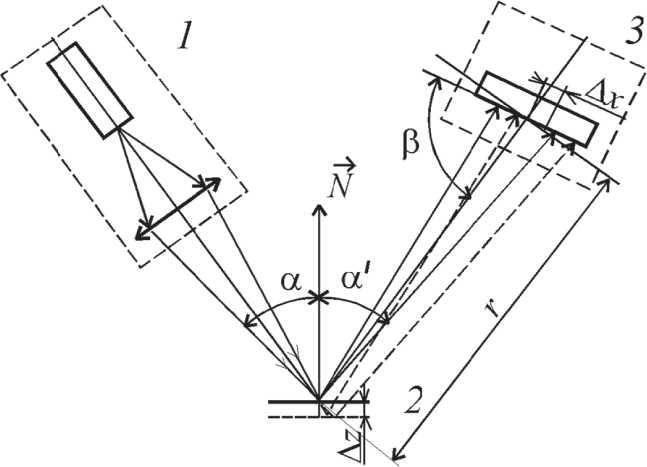
Рис. 1. Схема разновидности триангуляционного метода, использованного в работе: 1 - источник излучения; 2 - контролируемая поверхность; 3 - матричный фотоприемник; N - вектор нормали к освещенной точке поверхности 2;

r (на данном рисунке) - расстояние от поверхности до фотоприемника;

A z - высота неровности на поверхности;

A x - смещение центра пятна зеркально отраженного пучка света на фотоприемнике 3;

а , а / - углы падения и отражения пучка света на поверхность 2

МОДЕЛЬ СИСТЕМЫ

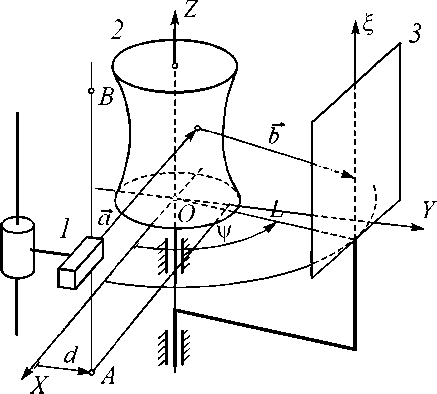
Исследование контролируемой поверхности ведется пучком света, который представлен одним лучом с нулевой поперечной шириной. Физической основой данной системы являются законы геометрической оптики. В оптической однородной среде свет распространяется прямолинейно. Это позволяет использовать пря- мые линии для анализа распространения све- та. Учет ширины пучка приводит к искажению формы светового пятна. Влияние этого фактора должно исследоваться экспериментально. На рис. 2 представлена оптико-механическая схема прибора [5]. Падающий на поверхность луч а перпендикулярен плоскости YOZ и зеркально отражается относительно вектора нормали N . Отраженный луч b фиксируется матричным фотоприемником. На основании законов геоме- трической оптики углы между номалью и этими лучами света равны между собой, и к тому же все три луча лежат в одной плоскости. Это опи- сывается системой векторных уравнений:

' - а х N _N х b

I a\ ⁼ |b | ,

( - a • N)_ b • N )

I, = | b | .

Информативным параметром является по- ложение пятна света на матричном фотопри- емнике. Оно измеряется в сферической системе координат с центром на оси OZ, там, где эту ось пересекает горизонтальная плоскость, в которой лежит падающий луч. Горизонтальный угол v отсчитывается от оси OX (рис. 2), а вертикальный угол 6 - от указанной горизонтальной плоскости. Сканирование поверхности контролируемого объекта производится путем его разворота вдоль оси OZ и дискретного перемещения источника света на величину шага по прямой AB в точках с координатами zk = zk-1 + Az. Данные действия позволяют из векторных уравнений

(1), (2) получить математическую модель авто- матизированной системы (кругломера):

F y • b z ^- F z • b y = 0 ;

F b -F b xz zx ^b X ⁺ b y ^{2 +} b z²

F • b — F • b xy yx b + b y ² + b z²

• -    F z = 0 ;

• -    F y = 0 ;

F b + F -b + F -b xx yy zz

----1              --F = о .

V b x + b y + b z

При решении системы уравнений (3) - (6) необходимо осуществить переход в цилиндрическую систему координат с центром в точке O и осью OZ (рис. 2).

Координата фC во время сканирования радиального профиля, которое производится путем поворота поверхности 2 при неподвижных других элементах сканера, слегка колеблется вокруг своей средней величины. Координаты фифR монотонно изменяются от нуля или какой-либо начальной величины на 2п радиан или на минус 2п радиан, как показано на рис. 2.

Решение системы (3) – (6) может быть получено в форме дифференциального уравнения (ДУ) вида

d Tc- = Р c '^ф ( р c >  Ф R . Z r ) , d Ф c

где z _R - смещение источника излучения 1; р с -соответствует точке на поверхности 2 с координатой ф с , пояснения к остальным обозначениям см. на рис. 2.

При линеаризации правой части исходного дифференциального уравнения (7) в области средних значений ее аргументов приходим к ДУ:

а )

R о

( dH

( d ф

л

- a • H = b •£ + c-у ,

б )

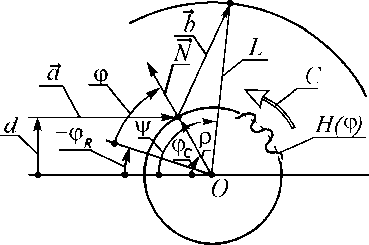
Рис. 2. Оптико-механическая схема прибора: а – общий вид; б – вид снизу;

1 – источник излучения; 2 – контролируемая поверхность; 3 - видеокамера; AB , С - направления сканирования; a – падающий и b – отраженный лучи света; y, x – координаты точки падения отраженного луча на фотоприемник; d – смещение источника излучения; L – радиус поворота каретки с видеокамерой; ф - азимутальная координата освещенной точки поверхности 2 в системе координат, связанной с этой поверхностью; ф R - угол поворота поверхности 2; ф C -азимутальная координата освещенной точки поверхности 2 в системе координат, связанной со сканером

J

где a , b , c получены из правой части исходного ДУ; H – высота профиля относительно окружности с радиусом R 0 ; 8 = ф - ф ; у = 0 - 6 . Индекс «0», а также черта означают среднее интегральное значение по радиальному профилю. Функции H , 8 , у имеют аргументом ф - азимутальную координату точки на радиальном профиле контролируемой поверхности.

В свою очередь линеаризованное ДУ (8) решается применением дискретного преобразования Фурье и решением является алгебраическая связь между гармониками Фурье-спектра профиля H одинаковой пространственной частоты и правой части ДУ.

Правая часть уравнения записывается в виде ряда Фурье:

[ N 2 ]

W ⁽ ф i ) = Е ^а j ■ cos ⁽ j ^- ф i ^{) +e} j ■ sin ⁽ j "ф i ) .⁽⁹⁾ j = 1

Коэффициенты данного ряда (9) вычисляются по формулам:

2 N - 1

a j =I7"Z W (ф i)" cos(j "ф i),

^N i = 0

2 N - 1

Pj=77'S W (ф i)" sin(j -Vi),

N i = 0

N - 1

a N 2 = 17-S(" 1)i- W (фi) •

^N i = 0

Таким образом, нам удалось найти связь между параметрами гармоники Фурье-спектра функций e и у соответствующей гамоники Фурье-спектра высот H .

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

Лабораторный макет прибора (рис. 3) был создан в Самарском филиале Физического института им. П. Н. Лебедева РАН. О его технических характеристиках сообщалось на конференции «Высокие технологии в машиностроении» в Санкт-Петербурге в 2008 году.

Предварительные результаты серии измерений с целью оценки их основной погрешности приведены в [6]. Отметим, что при этом прибор обеспечивал дискретность показаний с радиального профиля 600 отсчетов при контроле желоба внутреннего кольца шарикоподшипника типа 201. При этом радиус радиального профиля по дну желоба составлял 8,34 мм. В этих измерениях в источнике излучения в приборе использовался полупроводниковый лазер ближнего инфракрасного диапазона с длиной волны 0,78 мкм. Диаметр диафрагмы, ограничивающей параллельный коллимированный пучок

Рис. 3. Оптико-механический блок прибора:

1 – источник излучения;

2 – контролируемая поверхность; 3 – фотоприемник лазера, составлял 3 мм, в пределах ее апертуры распределение мощности пучка лазера было близким к равномерному.

ОБСУЖДЕНИЕ

По результатам статистического анализа этих измерений были определены основные факторы погрешности измерений. Наиболее важный из них связан с качеством узла поворота контролируемой детали. Сделан вывод о том, что, во-первых, прибор может достичь предельной погрешности измерений, требуемых стандартом [7] (радиальная погрешность 0,05 мкм). Кроме того, уже в этой версии прибор уверенно выявлял дефекты формы поверхности для части квалитетов колец подшипников в соответствии с методикой [8]. Однако прибор нуждается в усовершенствовании, его метрологические характеристики могут быть улучшены. Это связано также с переходом на более коротковолновый излучатель – полупроводниковый лазер с длиной волны излучения 0,405 мкм (фиолетовый цвет). При уменьшении параметра L прибора с 35 до 20 мм это дает требуемую методикой дискретность отчетов радиального профиля 2000 на оборот. При этом диаметр ограничивающей диафрагмы должен быть увеличен до 5 мм при сохранении равномерной освещенности в пределах ее апертуры. Это показали расчеты и эксперименты, сделанные авторами.

Учитывая недостаток финансирования разработки, мы предлагаем сбор и предварительную обработку данных проводить там, где для этого есть технические возможности, а вычис- ления, связанные с получением профиля и контурных картин поверхности изделия, контролируемого прибором, а также статистическую обработку полученных данных, выполнять в «облаке».

СТРУКТУРАИ ФУНКЦИОНАЛ КОМПЛЕКСА

Входной сигнал в программном комплексе – это файл, в котором в символьных кодах записаны зависимости г ( ф ) и у ( ф ) для радиального профиля контролируемой поверхности, а также параметры настройки оптической схемы и дискретность сканирования по ϕ и z . Комплекс обрабатывает сразу целую серию таких файлов, полученных при повторных измерениях, для каждого из файлов рассчитывает H ( ϕ ) и статистические параметры отклонений от круглости, включая границы доверительного интервала, попутно оценивая вероятность принадежности выборки к нормальному закону распределения. Кроме того, оценивается и погрешность в каждом отсчете радиального профиля H ( ϕ ), при условии, если серия измерений выполнена при одинаковом начальном положении контролируемой детали и координате z .

На рис. 4 представлена диаграмма вариантов использования автоматизированной системы. Отметим, что здесь слово «волнистость» понимается как любое отклонение от круглости, по выбору пользователя.

Автоматизированная система разрабатывается на языке высокого уровня Java с применением Spring Framework и позволяет производить вычисления в многопользовательском режиме.

ЗАКЛЮЧЕНИЕ

Описана физическая и математическая модель лазерного кругломера, приведена структура и функционал его программного комплекса, которые отличаются распределенностью вычислений. Авторы в своем предложении учли экспериментальные результаты, полученные ими ранее.

Авторы благодарят Белопухова В.Н. за разработку основы аппаратно-программного комплекса, Понявина Ю.О. и Чигарева А.С. за разработку «локальной» версии программы статистического анализа результатов измерений экспериментального лазерного кругломера, а также Треумова В.Д. и Попика С.И. за помощь в расчетах параметров источника излучения в приборе.

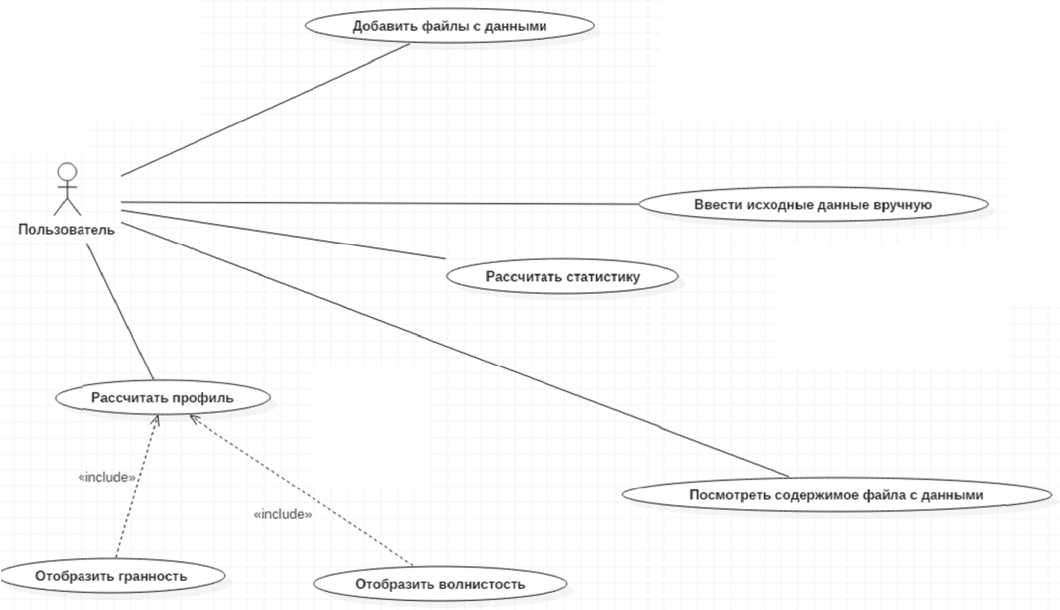
Рис. 4. Диаграмма вариантов использования автоматизированной системы