Экспериментальный способ построения программных движений роботизированной платформы с инсектоморфным движителем

выявления фундаментальных закономерностей, информацию об окружающей среде необходимо получать постоянно, в течение длительного периода времени. Проведение длительных экспедиций для постоянного круглогодичного получения информации и проведения замеров интересующих показателей также экономически не обосновано из-за географической удаленности и труднодоступности мест мониторинга. Одним из возможных решений данной проблемы может стать применение мобильных автономных робототехнических средств для выполнения работ, связанных с экологическим мониторингом и контролем за состоянием окружающей среды. На данный момент в мире для использования в мобильных робототехнических комплексах применяются колесные и гусеничные движители. Однако в процессе эксплуатации возможно появление ситуаций, когда работа мобильных роботов с колесными и гусеничными движителями сильно затруднена, а порой и невозможна. При работе в особо трудных условиях (на болотистых почвах, на льду, сыпучем песке, бездорожье и др.) обычные колесные и гусеничные движители не обеспечивают нормальной проходимости, в этих случаях необходимо использовать движители специальной конструкции. К таким движителям относятся в т.ч. и шагающие движители.

Использование шагающего способа передвижения мобильных роботов даёт качественный рост ряда основных показателей по сравнению с транспортными средствами, использующими традиционные колесные и гусеничные движители. Мобильные роботы с шагающими движителями имеют высокие возможности адаптации к неровностям опорной поверхности, большую профильную проходимость, а также маневренность, допускающую в большинстве случаев перемещение робота в произвольном направлении. Имеется возможность осуществления разворота на месте, проводить работы на грунтах со слабой несущей способностью, а также возможность управления опорными реакциями для проведения стабилизации по углам крена и дифферента. Разработана математическая модель робота «Октопод-1» [4] с инсектоморфным шагающим движителем, кинематическая схема которого представлена на рис. 1 и 2.

Рис. 1. Кинематическая схема шагающего инсектоморфного движителя «Октопод-1»: 1 – корпус верхней рамы, 2 – привод горизонтального перемещения верхней рамы, 3 – направляющие верхней рамы, 4 – конечность инсектоморфного движителя, 5 – вертикальная вращательная пара пятого класса, 6 – привод поворота рам, 7 - корпус нижней рамы, 8 -направляющие нижней рамы, 9 - привод горизонтального перемещения нижней рамы

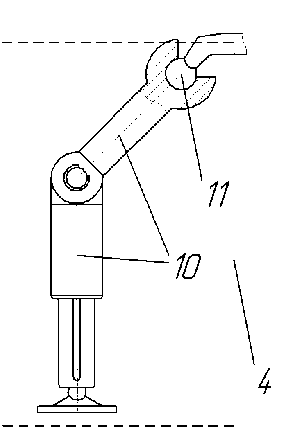
Рис. 2. Кинематическая схема ноги шагающего инсектоморфного движителя «Октопод-1»: 9 – звенья незамкнутой кинематической цепи, связанные вращательной парой пятого класса, 10 – вращательная пара четвертого класса.

Если принять за k число звеньев механиз -ма, то общее количество степеней свободы до соединения в кинематическую цепь равно 6k. При обозначении имеющихся кинематических пар одного класса как pi (i – номер класса), число накладываемых условий связи ∑ ipi , а i=1

число степеней свободы

N = 6 k - Z iPi i=1

Если одно из звеньев считается неподвижным, то число степеней свободы

N=6 n- z p

i = 1

где n=k –1 - число подвижных звеньев, k - число звеньев кинематической цепи. Число обобщенных координат определяется структурной формулой (2). Таким образом, число степеней свободы каждой механической конечности будет равным

N = 6 k - Z ip_t= 6 • 2 - (4 + 5) = 3

i = 1

Общее число степеней свободы механизма при условии наличия в инсектоморфном движителе восьми конечностей представляющих собой незамкнутую кинематическую цепь, в таком случае равно 24. Поворотный шарнир и поступательные пары пятого класса, обеспечивающие относительное перемещение верхней и нижней рам добавляют механизму 3 степени свободы. Таким образом, общее число степеней свободы 27. Подобная конструкция робота с инсекто-морфным шагающим движителем может быть представлена как многозвенная механическая система. Схема математической модели робота представлена на рис. 3.

Математическая модель робота представляется в виде многозвенной механической системы относительно неподвижной системы координат 0XYZ , с геометрическим центром корпуса робота показанном на рисунке 3, связана система координат 0X 1 Y 1 Z 1 . Относительное положение центра отсчета подвижной системы координат определяется радиус-вектором R 01 . Положение верхней и нижней частей робота относительно корпуса определяется векторами _               *

R ₁₂ и R ₁₃ соответственно. Определить их возможно зная геометрические параметры механической конструкции и координату x 1 точек А и В. Из известных заранее геометрических параметров конструкции однозначно определяются век *                *

торы R 31 и R 32 .

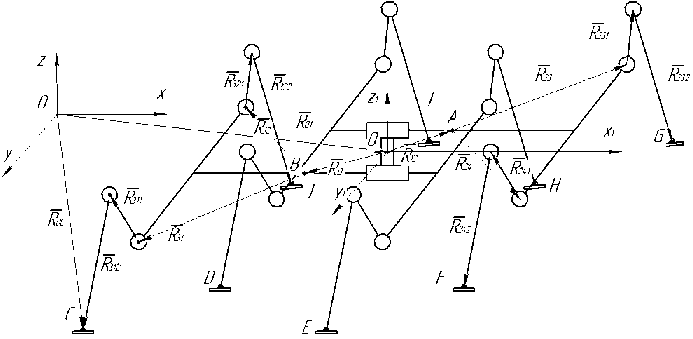
Рис. 3. Схема инсектоморфного движителя «Октопод -1»

Таким образом положение опорной точки каждой ноги в подвижной системе координат определяется геометрической суммой пяти векторов. Для первой ноги нижней рамы такая сумма запишется в виде ---------* --------* -------* --------* ----------* ---------- *

^R C = ^R 01 ⁺ R 13 ^{+ R} 31 ^{+ R} 311 ^{+ R} 312       (4)

Однозначное положение робота в неподвижной системе координат описывается системой из восьми векторных уравнений:

<

* R 0 C	* = R 01	--------* + R 13	* + R 31	* + R 311	------------* + R 312
* R 0 J	* = R 01	-------* + R 13	--------* + R 32	----------* + R 321	* + R 322
----------* R 0 H	-----------* = R 01	• --------------* + R 13	---------* + R 33	----------* + R 331	----------* + R 332
* R 0 E	* = R 01	* + R 13	* + R 34	* + R 341	* + R 342
----------* R 0 D	---------* = R 01	--------* + R 12	---------* + R 21	------------* + R 211	----------* + R 212
----------* R 0 I	* = R 01	--------* + R 12	--------* + R 22	----------* + R 221	----------* + R 222
* R 0 G	* = R0 1	---------* + R 12	* + R 23	* + R 231	----------* + R 232
----------* R 0 F	---------* = R 01	--------* + R 12	--------* + R 24	----------* + R 241	----------* + R 242

При построении математической модели использовались следующие допущения:

• 1.    Механическая система состоит из абсолютно твердых тел.

• 2.    На механические звенья наложены идеальные связи.

• 3.    Параметры робота, в т.ч. длины механических звеньев, известны заранее.

• 4.    Углы относительного поворота звеньев известны и определяются данными полученными от системы очувствления.

• 5.    Робот перемещается по недеформируе-мой абсолютно жесткой плоской поверхности

• 6.    Робот находится в поле сил тяжести, направление силы тяжести совпадает с нормалью, проведенной к поверхности X0Y.

• 7.    При расчете кинематики и алгоритмов перемещения, массы звеньев робота не учитываются.

совпадающей с плоскостью X0Y неподвижной системы координат.

При создании конструкции робота с ин-сектоморфным шагающим движителем применен блочно-модульный принцип построения электромеханических структур на базе унифицированных автоматизированных электроприводов с программируемыми микроконтроллерами. Подобные схемы используются для построения конструкций мобильных роботов и систем управления многодвигательными электроприводами машин и агрегатов типовых групп технологического и транспортного оборудования, а также автоматизированных технологических комплексов базовых отраслей промышленности.

Блочно-модульный принцип позволяет повысить ремонтопригодность системы в целом, быстро заменять вышедшие из строя унифицированные модули, перестраивать их структуру, создавать робототехнические схемы с гибкими функциональными возможностями, обеспечивающие рациональное использование информационных и энергетических ресурсов. В рамках существующей робототехнической системы все блоки выполняются совместимыми по интерфейсу, т.е. совместимыми по параметрам и характеристикам носителей информации, похожими по конструктивному исполнению, с унифицированными устройствами коммутации. Блоки создаются посредством монтажа и коммутации отдельных модулей, которые, в свою очередь, собираются из отдельных деталей и узлов.

Каждая нога инсектоморфного движителя является пространственным механизмом, представляющим собой незамкнутую кинематическую цепь, состоящую из нескольких базисных звеньев соединенных между собой шарнирами и одного свободного концевого звена. За счет наличия свободного звена появляется возможность выбора мест постановки опорных стоек в пределах зоны достижимости механизма ноги. Это расширяет адаптационные возможности мобильных робототехнических систем построенных на базе шагающего инсектоморфного движителя в сравнении с другими движителями. Звенья связаны между собой поступательными и вращательными парами пятого класса. Относительное перемещение звеньев робота происходит за счет управляемого движения приводных электродвигателей с передаточными механизмами, выполненными в виде модуля содержащего в себе электродвигатель, редуктор, набор датчиков обратной связи и управляющий микроконтроллер. Каждый модуль управляется посредством электронно-вычислительного блока, выполняющего вычисление законов программных движений для каждого привода в зависимости от задаваемого оператором маршрута движения на основании информации полученной от системы датчиков обратной связи.

Кинематика движения ноги инсекто-морфного робота рассчитывается с помощью методов теоретической механики [5, 6]. При перемещении каждой из восьми ног кинематическая схема инсектоморфного движителя допускает бесконечное число алгоритмов перемещения опорной точки концевого звена шагающего аппарата между двумя точками пространства. В связи с этим встает вопрос выбора алгоритма перемещения с точки зрения различных критериев оптимальности. Например, в качестве такого критерия может служить критерий, отвечающий за непроизводительные потери в электродвигателях, связанные с нагревом обмоток. Нагрев двигателя, а, следовательно, тепловые потери, пропорциональны квадрату тока якоря, и, следовательно, пропорциональны квадрату нагрузки на электродвигатель. В случае, когда известны граничные условия на концах искомой функции, при перемещении опорной точки ноги шагающего аппарата, такой функционал можно представить в виде[7, 8]:

t 2

I = aKF•(t)]dt , (6) ti

где I – критерий оптимальности, α - коэффициент пропорциональности, F дв – усилие в приводном электродвигателе.

Задача нахождения искомой функции доставляющей минимум функционалу решается методами классического вариационного исчисления, при этом в зависимости от граничных условий возможно получение различных законов при перемещении опорного звена между двумя точками пространства. Существуют различные теоретические методы нахождения программных законов движения исполнительных механизмов в зависимости от требуемого закона перемещения робота в неподвижной системе координат 0XYZ. Такие законы перемещения определяются методами аналитической механики.

Для экспериментальной проверки полученных теоретических законов изменения углов относительного поворота звеньев ноги шагающего инсектоморфного движителя, в зависимости от траектории движения опорной точки механизма, создан экспериментальный стенд. Стенд состоит из персонального компьютера, двух аналого-цифровых преобразователей «Mas-tech» 1 с цифровым выходом для подключения к ПК, кронштейна 2 , потенциометров 3 , двух звеньев переменной длины 4 , опорного конуса 5 . Звенья соединяются между собой, а также крепятся на кронштейне, с помощью втулок и вала потенциометра. АЦП имеет возможность снимать показания аналоговых датчиков с высокой частотой, что повышает точность полученных программных законов движения звеньев робота. При перемещении опорного конуса между двумя заданными точками пространства изменяется угловое положение звеньев робота, чему соответствует пропорциональное изменение сопротивления потенциометра. Данные об изменяющемся сопротивлении потенциометра, в зависимости от положения опорного конуса, передаются с помощью аналогово-цифровых преобразователей на компьютер. По данным датчиков строятся графики зависимости изменения углов положения от времени или координаты. При перемещении опорного конуса между двумя точками возможно получение семейства кривых, характеризующих многообразие алгоритмов перемещения конечности инсекто-морфного движителя.

С помощью экспериментального стенда строятся законы программного перемещения отдельных звеньев механизма шагания, а также проводится моделирование движения всего робота. Стенд моделирует движение каждой из восьми конечностей инсектоморфного движителя, каждая из которых состоит из шарнирного двухзвенника, соединенного с корпусом сферическим шарниром, на свободном конце которого закреплена опорная плита [5, 6]. Фото стенда показано на рис. 4.

Рис. 4. Экспериментальный стенд: 1 – мультиметр, 2 – кронштейн, 3 - потенциометры, 4 – звенья переменной длины, 5 – опорный конус

Выводы: разработки шагающих машин и роботов затруднены сложностью динамических взаимосвязей составляющих движения шагающего робота со многими приводами, отсутствием мобильных энергетических установок небольшой массы, а также отсутствием теории оптимального движения шагающих аппаратов. Шагающие инсектоморфные движители являются новыми и полностью не исследованы. Перспективы развития таких систем обусловлены нахождением оптимальных с точки зрения энергозатрат алгоритмов перемещения. Движители подобной конструкции перспективны для применения в многофункциональных наземных и подводных транспортно-технологических комплексах, робототехнических системах для экологического мониторинга, гуманитарного разминирования, а также для исследования других планет и применения в космической технике.

Работа выполнена при поддержке РФФИ, проект №14-01-31376, №15-08-04166,№15-41-02578