Экспертная оценка программных продуктов для восстановления пропусков в массивах данных

Причинами появления пропусков в массивах данных являются невозможность получения или обработки, искажение или сокрытие информации. Для восстановления пропущенных значений в массиве данных используются различные программные средства, позволяющие производить импутирование их различными алгоритмами.

В данной статье проведен анализ программных продуктов (DeductorStudio, SPSS Statistics, MS Excel, Stata, SAS/ETS Software) позволяющих восстанавливать пропущенные значения, и определенны их весовые коэффициенты критериев качества методом Саати [1,4].

Основываясь на потребностях пользователей по отношению к программным средствам, позволяющим производить импутирование, были выбраны следующие показатели в качестве критериев для сравнительного анализа аналогов программ:

• 1.    A1 - Набор алгоритмов восстановления

• 2.    A2 - Точность восстановления данных

• 3.    A3 - Скорость восстановления данных

• 4.    A4 - Формат входных данных

• 5.    A5 - Простота работы с ПО

Используя аналитическую иерархическую процедуру Саати, определим вес каждого критерия качества [3,6,7]. Правила заполнения матрицы парных сравнений представлены в таблице 1.

Таблица 1. Значения коэффициентов матрицы парных сравнений

X ij	Значение
1	i -ый и j -ый критерий примерно равноценны
3	i -ый критерий немного предпочтительнее j -го
5	i -ый критерий предпочтительнее j -го
7	i -ый критерий значительно предпочтительнее j -го
9	i -ый критерий явно предпочтительнее j -го

Матрица парных сравнений, средние геометрические и веса критериев представлены в таблице 2.

Таблица 2. Матрица парных сравнений, средние геометрические и веса критериев.

	A1	A2	A3	A4	A5	Среднее геометрическое	Веса критериев
A1	1	3	5	7	9	3,94	0,50
A2	1/3	1	5	5	7	2,26	0,29
A3	1/5	1/5	1	3	5	0,90	0,11
A4	1/7	1/5	1/3	1	7	0,58	0,07
A5	1/9	1/7	1/5	1/7	1	0,21	0,03
Сумма						7,89	1,00

Диаграмма весовых коэффициентов для критериев A1, A2, A3, A4,

A5 представлена на рисунке 1.

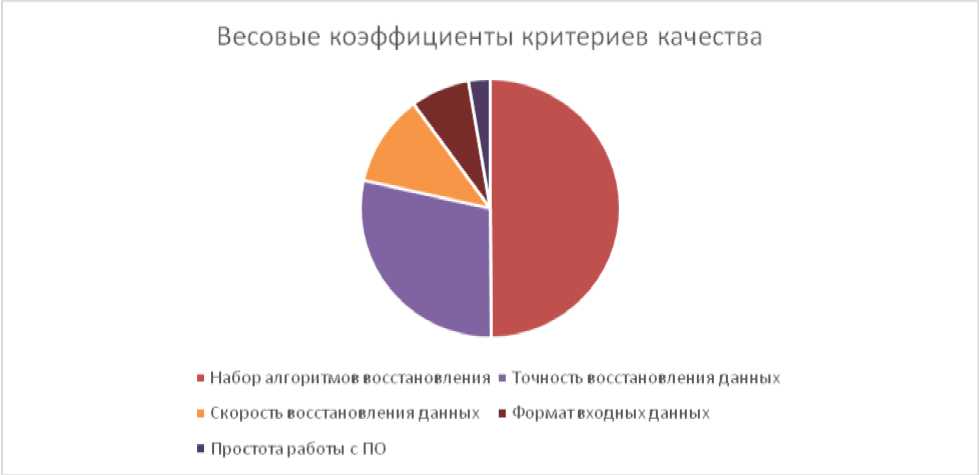
Весовые коэффициенты критериев качества

■ Простота работы с ПО

■ Скорость восстановления данных ■ Форматвходных данных

Набор алгоритмов восстановления ■ Точность восстановления данных

Рисунок 1. Весовые коэффициенты критериев качества

Проведем проверку матрицы парных сравнений на непротиворечивость. Суммы столбцов матрицы парных сравнений: R 1 =1,79; R 2 = 4,54; R 3 = 11,53; R 4 = 16,14; R 5 =29.

Рассчитаем вспомогательную величину L, просуммировав произведения сумм столбцов матрицы и весовые коэффициенты: L = 5,48. Индекс согласованности ИС = (L-N)/(N-1) = 0,12.

Величина случайной согласованности для размерности матрицы парных сравнений: СлС = 1,12. Отношение согласованности ОС=ИС/СлС = 0,11. не превышает 0.2, поэтому уточнение матрицы парных сравнений не требуется.

Используя полученные коэффициенты, определим интегральный показатель качества для следующих программных продуктов, направленных на восстановление пропусков в данных:

• 1.    DeductorStudio;

• 2.    SPSS Statistics;

• 3.    MS Excel;

• 4.    Stata;

• 5.    SAS/ETS Software.

Выберем категориальную шкалу от 0 до 7 (где 0 – качество не удовлетворительно, 7 – предельно достижимый уровень качества) для функциональных возможностей выбранных программ [4,8].

Значения весовых коэффициентов ai, соответствующие функциональным возможностям аналогов программ:

• 1.    Набор алгоритмов восстановления: a 1 = 0,50;

• 2.    Точность восстановления данных: a₂ = 0,29;

• 3.    Скорость восстановления данных: a 3 = 0,11;

• 4.    Формат входных данных: a₄ = 0.07;

• 5.    Простота работы с ПО: a 5 = 0.03;

где ∑a i = 1.

По выбранной шкале определим количественные значения функциональных возможностей X ij (таблица 3) и вычислим интегральные показатели качества для выбранных программ.

Критерии	Весовые коэффициенты	Программные продукты					Базовые значения
		DeductorStudio	SPSS Statistics	MS Excel	Stata	SAS/ETS Software
Наборалгоритмов восстановления	0,50	7	7	1	5	5	5,00
Точность восстановления данных	0,29	6	6	3	4	5	4,80
Скорость восстановления данных	0,11	6	7	4	4	5	5,20
Формат входных данных	0,07	6	6	2	5	4	4,60

Простота работы с ПО	0,03	5	5	6	4	4	4,80
Интегральные показатель качества Q		6,47	6,58	2,13	4,57	4,90	4,93

Таблица 3. Интегральные показатели качества.

где Q j = ∑a i * X ij – интегральный показатель качества для j -го программного продукта.

Построим лепестковую диаграмму интегрального показателя качества каждого программного продукта (рисунок 2).

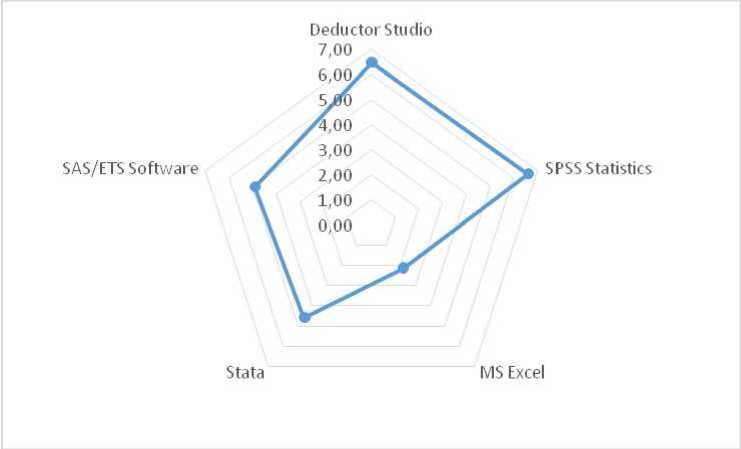
Рисунок 2. Лепестковая диаграмма интегральных показателей качества программ

Значения характеристик функциональных возможностей (критериев) представлены в виде лепестковой диаграммы на рисунке 3.

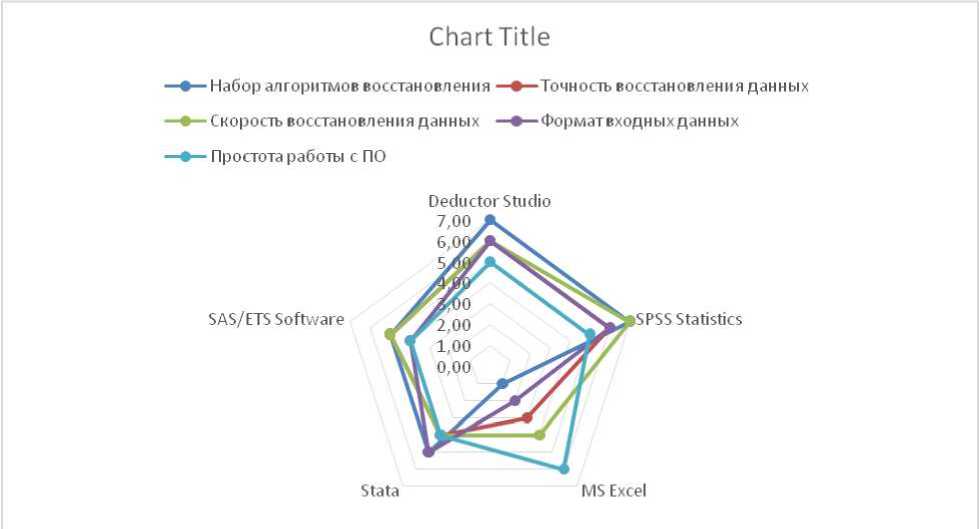
Рисунок 3. Лепестковая диаграмма значений функциональных характеристик

Сравнительный анализ программных продуктов для восстановления пропусков в массиве данных показал, что из всех программных аналогов только DeductorStudio и SPSS Statistics имеют значение интегрального показателя качества, превышающий базовое значение, а у остальных программных аналогов оно оказалось ниже. Так же анализ показал, что DeductorStudio и SPSS Statistics надо улучшать показатели по таким критериям как: «Точность восстановления данных» и «Формат входных данных».

Предлагаемая методика экспертной оценки программных продуктов позволила количественно оценить их качество с точки зрения уровня реализуемых функций и выявила функции, которые не удовлетворительно реализованы в некоторых рассматриваемых программных продуктах.