Экстремум зависимости напора электромагнитного насоса для жидкого металла от частоты питающего тока

Электромагнитные насосы для жидких металлов нашли широкое применение в металлургической промышленности [1]. Также они входят в состав атомных и термоядерных установок [2]. В электромагнитном насосе для генерации перепада давления используются электромагнитные силы, которые возникают при взаимодействии электрического тока и магнитного поля в рабочем участке канала. Различают два типа электромагнитных насосов по способу создания электромагнитных сил в канале: кондукционные и индукционные. В первом случае электрический ток подводится к каналу через его стенки, а магнитное поле создается внешним источником, которым может служить постоянный магнит, электромагнит или магнитное поле тока, намагничивающее ферромагнетики [3, 4]. Во втором случае электрический ток генерируется в электропроводной среде вследствие того, что на нее воздействует

магнитное поле с переменным потоком. Наибольшее распространение как в металлургии, так и в атомной промышленности получили индукционные насосы бегущего магнитного поля [5, 6]. К настоящему времени не создана универсальная конструкция, что вызывает необходимость поиска наилучших параметров устройств в каждой конкретной задаче [7–11].

Самым используемым в металлургической и атомной промышленности является линейный индукционный электромагнитный насос бегущего поля с коаксиальным щелевым цилиндрическим каналом [2, 12]. В таком насосе жидкий металл под действием электромагнитных сил протекает по каналу между двумя вложенными трубами разного диаметра. Геометрические и физические характеристики всей системы существенно влияют на производительность электромагнитного насоса. Для поиска наилучших характеристик необходимо рассматривать полную математическую модель процесса [10]. Благодаря математическому моделированию создана линейка электромагнитных насосов данного типа для атомной промышленности. Опыт авторов по разработке и приемо-сдаточным испытаниям подобных устройств показал зависимость производительности от величины электропроводности расплавленного металла, которая в свою очередь обусловлена составом расплава. В связи с этим особого внимания заслуживает чистота теплоносителя на атомных электростанциях.

Жидкие металлы, применяемые в качестве теплоносителей в атомных реакторах на быстрых нейтронах, химически активны. Состав примесей, присутствующих в исходном металле, например, натрии, и появляющихся в процессе эксплуатации установок, разнообразен [12]. Так, окислы забивают тонкие каналы, мешают работе устройств, ухудшают характеристики теплообмена, а также меняют электропроводность натрия, что негативно сказывается на работе электромагнитных аппаратов (например, насосов и расходомеров). Контроль химического состава теплоносителя и его очистка — важные задачи при эксплуатации реакторов [2, 12, 13]. На атомных станциях на быстрых нейтронах основным способом очистки жидкого натрия от примесей является холодная фильтр-ловушка [2, 13], принцип действия которой состоит в использовании температурной зависимости растворимости примесей в теплоносителе. Растворимость главной нежелательной примеси в натрии — оксида натрия, уменьшается с падением температуры, что приводит к кристаллизации примесей как на охлаждаемых поверхностях, так и в объеме ловушки. При кажущейся простоте и эффективности ловушки у нее есть недостатки: ограниченный объем накопителя примесей, малый расход, недостаточная глубина очистки и другие проблемы. Это заставляет постоянно развивать существующие технологии очистки жидкометаллического теплоносителя.

Высокая электропроводность жидких металлов открывает возможность прибегать к очистке методами, основанными на электродинамических процессах [14–16]. В таком случае жидкий металл одновременно подвергается воздействию электрического тока и магнитного поля. Возникающая электромагнитная сила по-разному действует на компоненты среды, имеющие различную электропроводность [17, 18]. Ключевой особенностью технологии электромагнитной сепарации является создание сепарирующих электромагнитных сил в электропроводной среде бесконтактным способом [17, 19, 20]. Это позволяет применять каналы с простой геометрией, а также делает ненужной и механическую фильтрацию для отделения включений. При удачной реализации такой методики ее можно рекомендовать к использованию в металлургической и атомной промышленности.

В технологии электромагнитной очистки жидкометаллического теплоносителя одной из важнейших задач является разработка методов оперативного и надежного контроля свойств расплава, главное из которых — электропроводность. Существующие [2] и разрабатываемые [21] методики недостаточно точны и удобны для применения. Все они требуют отдельных устройств, которые необходимо калибровать. Система как механической, так и электромагнитной очистки жидкометаллического теплоносителя представляет собой совокупность следующих элементов: трубопровод, электромагнитный насос, электромагнитный расходомер, два манометра (на входе и выходе насоса), запорный вентиль, сепарирующей аппарат, устройство измерения свойств. Встает вопрос: «Можно ли исключить из этой цепочки устройство измерения свойств, а его функцию возложить на какие-либо из оставшихся элементов?» Поиску ответа и посвящена данная работа.

Целью работы является исследование зависимости перепада давления, развиваемого индукционным электромагнитным насосом с коаксиальным каналом, от частоты питающего тока для различных наборов управляющих параметров аппарата, обеспечивающих режимы его работы. Именно эта характеристика выбрана как наиболее обещающая с точки зрения обнаружения особенностей, которыми можно воспользоваться для измерения электропроводности. В работе [10] получен ряд характеристик, имеющих экстремумы, но они обусловлены геометрическими размерами электромагнитного насоса, поэтому опираться на них в данной задаче нельзя. Здесь, наоборот, изучаются характеристики электромагнитного насоса с фиксированными геометрическими параметрами. Исследование проводится путем математического моделирования, а верификация модели осуществляется на основе лабораторных экспериментальных исследований с жидким металлом, свойства которого хорошо известны и стабильны.

2.    Постановка задачи

Рассматривается электромагнитный насос, который представляет собой совокупность канала и индуктора (Рис. 1). Канал 1 образуют две цилиндрических трубы из нержавеющей стали длиной 464 мм.

Внешняя труба имеет наружный диаметр 107 мм и толщину стенки 2,5 мм, наружный диаметр внутренней труба равен 94 мм, а толщина стенки 2 мм. В пространстве между трубами находится жидкий металл. Канал внутренней трубы заполнен ферромагнетиком. Индуктор состоит из 12 катушек 2 , намотанных медным проводом, и 8 ферромагнитных сердечников 3 . Сердечники 3 имеют сложную форму с вытянутыми зубцами, между которыми размещаются катушки 2 . Длина индуктора 424 мм, наибольшая ширина 362 мм. Для создания бегущего магнитного поля обмотки подключаются к трехфазной электрической сети. Возможны два способа их подключения. В первом случае сдвиг фаз между соседними катушками равняется 60° (Тип 1), а во втором случае сдвиг фаз в 60° имеет место между двумя последовательными парами катушек (Тип 2). Таким образом, в первом случае длина волны бегущего поля в два раза меньше, чем во втором случае. Бегущее магнитное поле создает электромагнитную силу, которая генерирует течение. Основными характеристиками процесса являются сила тока I , частота тока f , перепад давления в канале между входом и выходом dP , а также расход жидкого металла Q .

Особо следует подчеркнуть, что в данном исследовании интересны не сами характеристики электромагнитного насоса, хотя они и имеют большую практическую ценность, а вид их зависимости от частоты. По этой же причине не имеет смысла переход к безразмерным величинам, необходимый для обобщения результатов, так как абсолютные величины задаваемых и получаемых параметров, как будет видно далее, не играют роли при формировании заключительного вывода по работе. Поэтому объектом изучения выбран электромагнитный насос, который, по сравнению с теми насосами, которые используются в промышленности, не выдает большую производительность, но его конфигурация позволяет провести математическое моделирование на мелких сетках, а наличие у авторов точно изготовленного аналога для эксперимента дает возможность осуществить надежную верификацию модели путем сопоставления результатов.

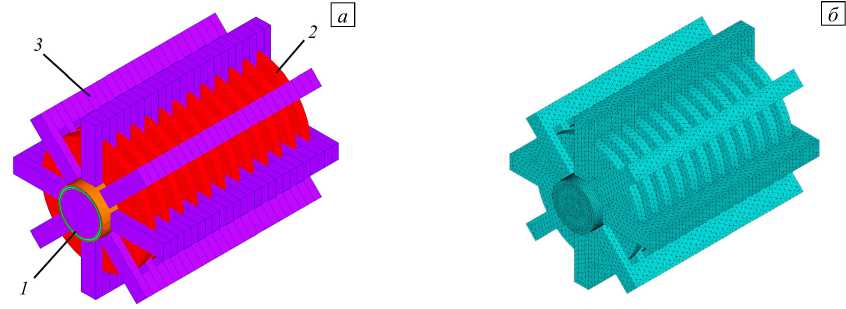
Рис. 1. Схема расчетной области электромагнитного насоса ( а ): 1 – канал, 2 – катушки, 3 – сердечники; сеточное разбиение для расчетов в электромагнитной части задачи ( б ); объем с окружающим пространством не показан

Математическая модель основана на уравнениях электродинамики сплошных сред, которые описывают процесс взаимодействия электрических и магнитных полей с движущимися электропроводными средами [22]. В общем случае одним из базовых уравнений является уравнение переноса магнитного поля движущейся электропроводной жидкостью:

— + Vx ( V x B ) = — A B . d t      ^{V 7} Re m

Здесь: t — время; B — индукция магнитного поля; V — скорость электропроводной среды; Re_m = V₀L 0 ацц ₀ — безразмерное магнитное число Рейнольдса, где V 0 — характерная скорость электропроводной среды, L 0 — характерный размер, а — электропроводность среды, ц — магнитная проницаемость движущейся среды, ц ₀ — магнитная постоянная. Число Re_m характеризует интенсивность процесса переноса магнитного поля движущейся средой. Предварительные оценки показали, что для значений перечисленных величин, достигаемых в данном исследовании, Re_m<<1 . Это означает, что переносом магнитного поля потоком электропроводной среды можно пренебречь [22]. Кроме того, оценочная дрейфовая скорость более чем на порядок превышает скорость движения в канале электропроводной среды, поэтому эффекты, связанные с проскальзыванием, можно не учитывать [4]. Таким образом, электродинамическую часть математической модели можно представить уравнениями Максвелла:

∇×E = -∂B/∂t,(3)

∇⋅B=0,(4)

∇⋅E=0.(5)

Расчетная область электродинамической части задачи состоит из совокупности непересекающихся объемов, соседние из которых имеют общие границы. В этих объемах содержатся катушки, ферромагнитные сердечники, трубопроводы, жидкий металл, окружающее пространство в некоторой окрестности вокруг индуктора. Закон Ампера (2) без учета тока смещения описывает генерацию исходного магнитного поля с помощью обмоток индуктора. В уравнении (2) приняты обозначения: j _c — переменная плотность тока, который течет по обмоткам, H — напряженность переменного магнитного поля, созданного током обмоток; поле j _c заключено в обмотках, а поле H — во всей расчетной области. Плотность тока совершает гармонические колебания с частотой f и меняется во времени. Воздействие магнитного поля H на объемы со средами, имеющими разные магнитные проницаемости µ , приводит к появлению в них намагниченности. Это учитывается в модели в виде выражения связи магнитной индукции и напряженности магнитного поля: B = µµ ₀ H . Для всех объемов, кроме ферромагнетиков, значение магнитной проницаемости µ слабо отличается от единицы. Для определения степени насыщения ферромагнетика отдельно выполняется расчет зависимости индукции магнитного поля от величины тока в обмотках. Предварительные расчеты показали, что в области исследуемых параметров насыщения ферромагнетиков не происходит, поэтому принимается, что магнитная проницаемость ферромагнетика постоянна, в вычислительных экспериментах она взята равной µ= 3 ⋅ 10³ Гн/м. Также считается, что все магнетики изотропны, а магнитные свойства внутри объемов — однородны. В силу этого связь индукции и напряженности выражается линейной функцией.

Переменное магнитное поле в свою очередь генерирует во всей расчетной области вихревое электрическое поле напряженностью E . Этот процесс представляется уравнением электромагнитной индукции (3). Возникающие магнитное и электрические поля имеют соленоидальный вид и описываются уравнениями (4) и (5). Электрическое поле (3) является электродвижущей силой, под действием которой в электропроводной среде зарождается вихревой электрический ток. Важно, что ферромагнитные части насоса изготовлены из тонких листов электротехнической стали, покрытой электроизолирующим лаком, а обмотка катушек создается из тонкого провода, также имеющего электроизоляцию. Поэтому генерация вихревых токов в ферромагнетиках и обмотках во внимание не принимается, а в объемах жидкого металла и труб этот процесс изображается в виде закона Ома:

j = σ E .

Наличие электрического тока и магнитного поля в электропроводной среде приводит к появлению объемной электромагнитной силы, которую имеет смысл учитывать только в жидком металле, твердые стенки не перемещаются:

f = j × B .

Граничные условия даются далее в общем виде; индексами помечены области со средой 1 и средой 2, которые различаются свойствами. На границах канала между расплавленным металлом и электропроводящими стенкам труб ставятся условия равенства нормальной и тангенциальной компонент плотности электрического тока:

j_{n 1} = j_{n 2},      σ ₂ j _{τ 1} =σ ₁ j _{τ 2},

и условия равенства магнитных индукций:

B n 1 = B n 2 ,     µ 2 B τ 1 =µ 1 B τ 2

Течение электропроводящей среды в коаксиальном канале в рамках принятого безындукционного приближения описывается уравнениями:

av ,      ,          1                  1

+(V⋅∇)V = - ∇P+ν∆V+ f, ∂t   ρρ

где (10) — уравнение Навье–Стокса с учетом действия электромагнитной силы, а (11) — уравнение неразрывности. Приняты обозначения: ν — вязкость, а ρ — плотность жидкого металла. Турбулентность учитывается путем использования ее стандартной k -ω модели. Выбор этой модели турбулентности определило ее успешное применение для решения задачи магнитной гидродинамики (см. [26], в которой выполнена верификация модели k -ω путем экспериментов). В расчетах жидкость содержится в объеме, который представляет собой коаксиальный канал. Для жидкости на боковых стенках канала ставится условие прилипания V = 0, на входе и выходе задается массовый расход, который равен нулю в стопорном режиме (при отсутствии расхода).

Для вычислений в электродинамической части задачи применялся модуль Emag программного комплекса ANSYS, использующий язык APDL. С его помощью реализованы многовариантные расчеты, в ходе которых варьировалось значение частоты, и по выражениям (2)–(5) определялись вихревые электрическое и магнитное поля, а по (6), (7) находились поля плотности тока и электромагнитной силы при учете граничных условий (8), (9). Вычисления в гидродинамической части задачи осуществлялись в модуле ANSYS Fluent на основе уравнений (10) и (11) методом конечных объемов. Все вычисления выполнялись на многопроцессорной технике. Среднее число элементов составляло: в электродинамической задаче 2·106, в гидродинамической задаче 5·106. Перенос данных с электродинамической сетки на гидродинамическую производила программа на языке Python. Сопряжение гидродинамического и электродинамического решений было однократным перед началом гидродинамических расчетов.

Экспериментальные исследования для верификации математической модели проводились на жидкометаллическом контуре с внутренним диаметром 20 мм (Рис. 2). Контур состоит из системы хранения металла 1 , расширительной емкости 2 , вакуумной системы 3 , используемой для заполнения контура металлом, газовой системы 4 , системы очистки 5 . Расход регулируется клапаном 6 , расход регистрируется кондукционным электромагнитным расходомером 7 . Расходомер откалиброван объемновесовым способом. Давление в контуре измеряется набором дифференциальных манометров «Метран» 8 . В контуре имеется система стабилизации и контроля температуры с помощью водяного охлаждения 9 и термопар 10 . Анализ информации в ходе эксперимента показал, что уровень изменения температуры не превышает 5°C градусов относительно показателя в комнате (25°C), что на электропроводности сказывается незначительно (ее изменение не более 1% [23]). Это является пренебрежимо малой величиной. Электромагнитный насос 11 с источником питания 12 соединяется с трубопроводом 13 контура посредством фланцев. Все показания контура передаются на компьютер платами сбора данных «National Instruments» и обрабатываются в системе «LabView». В качестве источника питания используется частотный регулятор напряжения Hyundai N700E, модель N700-750HF/900HFP, который позволяет выдавать стабильное контролируемое напряжение заданной частоты. Для обработки результатов применяется пакет MatLab.

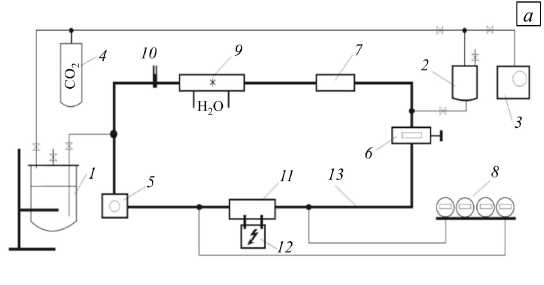
Рис. 2. Схема ( а ) и вид ( б ) экспериментального галлиевого стенда в ИМСС УрО РАН (Пермь) с установленным электромагнитным насосом (пояснения см. в тексте)

б

Эксперименты проводились на жидком металле, который представлял собой галлиевую эвтектику Ga86.3Zn10.8Sn2.9 (в индексах вес в процентах). Ключевое преимущество этой жидкости состоит в том, что она имеет температуру плавления +17°С. Физические свойства эвтектики при комнатной температуре следующие: плотность 6150 кг/м3, кинематическая вязкость 2.9·10–7 м2/с, электропроводность 2.6·106 См/м [23, 24]. Особое внимание уделяется поддержанию чистоты состава эвтектики в ходе исследования. Следует особо подчеркнуть, что окислы галлия не растворяются в галлии, а находятся в нем в виде отдельных включений, их небольшое количество неизбежно присутствует в металле. Именно они обеспечивают работоспособность методики измерения скорости жидкого металла, основанной на применении ультразвукового доплеровского анемометра (см., например, [25, 26]). Он регистрирует движение отдельных включений с последующим статистическим анализом, поэтому количество включений должно быть малым. Если же их содержание увеличивается, то проводить измерения нецелесообразно вследствие высокого уровня шума и нарастающей неопределенности. Перед проведением описанного в данной работе исследования было успешно проведено другое исследование [27] на этом же жидкометаллическом контуре, в ходе которого изучалась точность методики ультразвуковой анемометрии. Перед тем как приступить к исследованиям, запланированным в данной работе, эвтектика и контур были тщательно очищены от окислов. Это повысило достоверность физических свойств используемой эвтектики.

3.    Результаты

При подключении электромагнитного насоса к источнику трехфазного питания по катушкам начинает течь ток, который создает переменное бегущее магнитное поле. Магнитное поле пронизывает весь индуктор, в том числе ферромагнитные сердечники. В сердечниках появляется намагниченность. Силовые линии результирующей магнитной индукции замыкаются, в том числе в коаксиальном канале с жидким металлом. В канале переменное магнитное поле создает вихревой электрический ток. Его взаимодействие с магнитной индукцией приводит к генерации электромагнитной силы, которая оказывает влияние на жидкий металл.

На рисунке 3 в качестве примера приведены расчетные поля для одной совокупности параметров, которые иллюстрируют возникающие магнитогидродинамические процессы. В данном случае на катушках величина тока равнялась I = 7.5 А, а частота тока составляла f = 25 Гц. Показаны компоненты и проекции трехмерных полей на плоскость в осевом сечении канала, причем только для части канала вблизи пары зубцов, поскольку его длина существенно превышает ширину, и сложно отобразить информацию в полном объеме, однако легенды содержат весь диапазон значений, принимаемых полями. Рисунки 3 а , б дают представление о распределении радиальной и осевой компонент электромагнитной силы. Ее азимутальная компонента для таких конфигураций имеет существенно меньшее значение, поэтому она не отображается. Видно, что сила распределена неравномерно, наибольшего значения она достигает вблизи ферромагнитного сердечника. Именно в этих областях интенсивность силы является наибольшей. Радиальная компонента силы хотя и имеет тот же порядок величины, что и аксиальная, но не участвует в создании напора, который характеризуется перепадом давления в канале между его входом и выходом. Тем не менее, эта радиальная компонента силы создает локальное вихревое течение вблизи зубцов, которое хорошо заметно на рисунках 3 в–д . На рисунке 3 д прослеживается возникновение зоны рециркуляции. Без воздействия радиальной компоненты силы осредненное поле скорости металла было бы равномерным без появления вихревых структур.

Для верификации математической модели выполнены расчеты зависимости перепада давления от силы электрического тока, питающего обмотки, при фиксированной частоте в стопорном режиме. Значение электропроводности в расчетах было взято такое же, как у галлиевой эвтектики. При тех же параметрах электромагнитного насоса проведены эксперименты в гидравлическом контуре на галлиевой эвтектике.

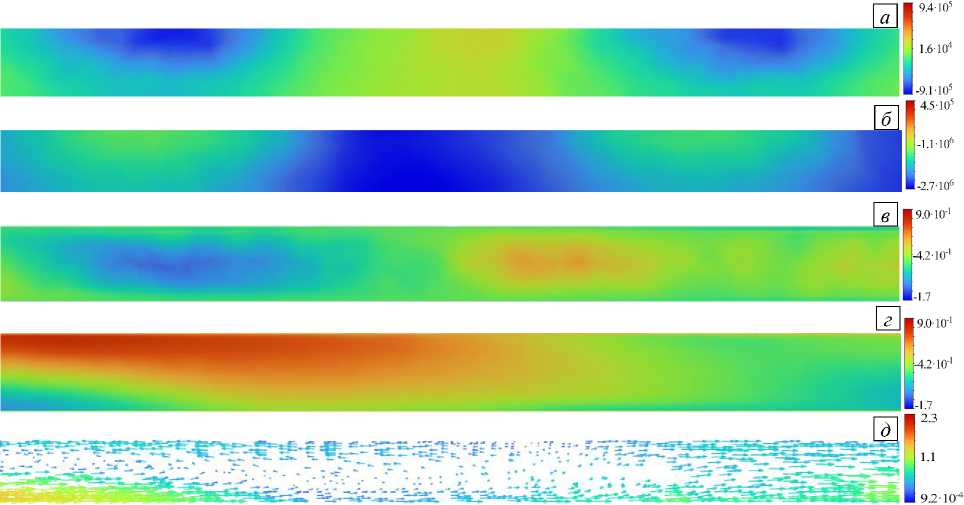
Рис. 3. Расчетные поля в аксиальном сечении канала с жидким металлом: радиальная ( а ) и осевая ( б ) компоненты плотности электромагнитной силы; радиальная ( в ) и осевая ( г ) компоненты скорости; векторное поле скорости ( д )

б

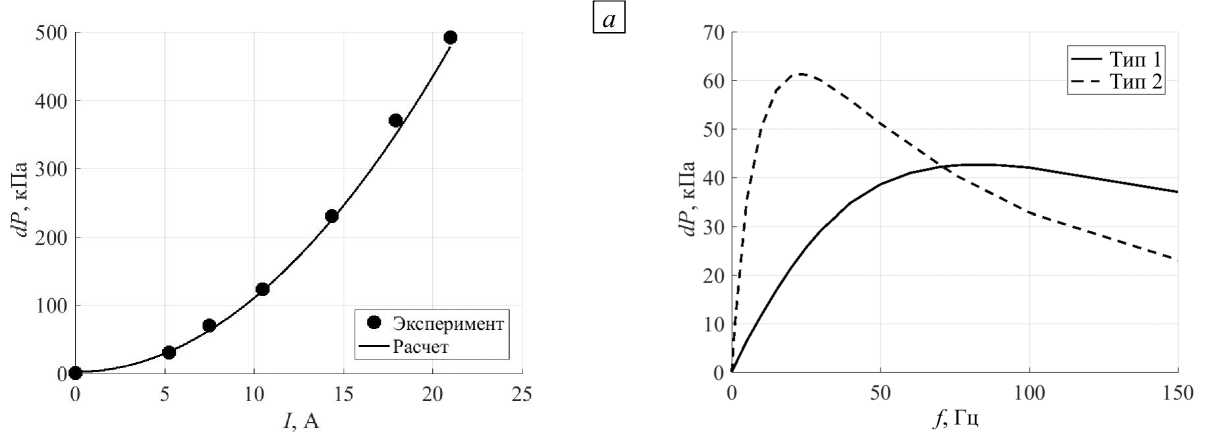
Рис. 4. Стопорный режим: зависимость перепада давления от силы тока при фиксированной частоте тока f = 25 Гц ( а ); расчетные зависимости перепада давления от частоты тока при фиксированном значении силы тока I = 7.5 А и подключении по Типу 1 и Типу 2 обмоток индуктора в трехфазную сеть для реализации бегущего поля ( б )

Результаты расчетов и экспериментов представлены на рисунке 4 а . Отличие результатов не превышает 3%. Расчетная кривая также хорошо повторяет квадратичный вид зависимости перепада давления от силы тока. Основной упор в дальнейших исследованиях сделан на стопорный режим, поэтому именно его верификации уделено наибольшее внимание.

Далее, посредством математического моделирования определены зависимости перепада давления от частоты электрического тока, который питает обмотки индуктора. Зависимости получены для стопорного режима, когда транзитное течение через канал отсутствует. На рисунке 4 б показаны примеры таких зависимостей, полученных для фиксированных значений силы тока I = 7.5А при двух разных типах подключения обмоток к трехфазной сети. Видно, что обе зависимости имеют экстремумы, каждый из которых достигается при разных значениях частоты питающего тока. Напомним, что подключение Типа 1 реализует длину волны бегущего магнитного поля более короткую, чем при Типе 2. В первом случае вид зависимости более пологий, чем во втором, а величина экстремального перепада давления примерно в полтора раза ниже. Таким образом, подключение Типа 2 является более предпочтительным для поиска положения экстремума, поэтому в дальнейших исследованиях рассматривался именно этот тип подключения. Посредством математического моделирования найдены те же зависимости перепада давления от частоты, но при разных значениях электропроводности жидкого металла. Некоторые из них продемонстрированы на рисунке 5. Видно, что положение максимума перепада давления для каждой кривой достигается при разных значениях частот. После этого, исходя из полученных расчетных данных, установлена зависимость от электропроводности частот f _m , обеспечивающих максимум перепада давления (см. Рис. 6).

Такое же исследование проделано с помощью экспериментального подхода. Для этого использовался галлиевый стенд с электромагнитным насосом. Возможность создания транзитного течения в контуре была исключена путем его перекрытия предусмотренным для этого вентилем. Определялась зависимость перепада давления между входом и выходом в канале от частоты электрического тока при фиксированном значении силы тока I = 7.5 А. Каждая точка на графике получалась при последовательном изменении значения частоты электрического тока с подстройкой для каждого из них значения силы тока до заданного фиксированного уровня, затем измерялся перепад давления. На рисунке 5 показана экспериментальная зависимость перепада давления от частоты тока, которая, как оказалось, во-первых, повторяет форму расчетных кривых, а во-вторых, также имеет экстремум. Как и в расчете с использованием аппроксимации данных измерения и анализа была определена частота f _m , при которой перепад давления принимает максимальное значение. Эксперимент проводился при фиксированной температуре, для которой известна величина электропроводности названной выше галлиевой эвтектики. Если нанести эту экспериментальную точку на расчетную зависимость частот f _n , обеспечивающих максимум перепада давления, от электропроводности (Рис. 6), то, как видно, она наиболее близка к расчетному значению частоты f _m , полученному при значении электропроводности 2.6·10⁶ См/м Такую же электропроводность имеет галлиевая эвтектика. Таким образом, во-первых, с помощью еще одного исследования — поиска положения экстремума на зависимости перепада давления от частоты, выполнена верификация математической модели; при этом результаты математического моделирования и эксперимента хорошо согласуются. Во-вторых, показано, что расчетным путем можно находить истинное значение электропроводности путем сопоставления с экспериментом. Об этом более подробно будет сказано в заключительном разделе.

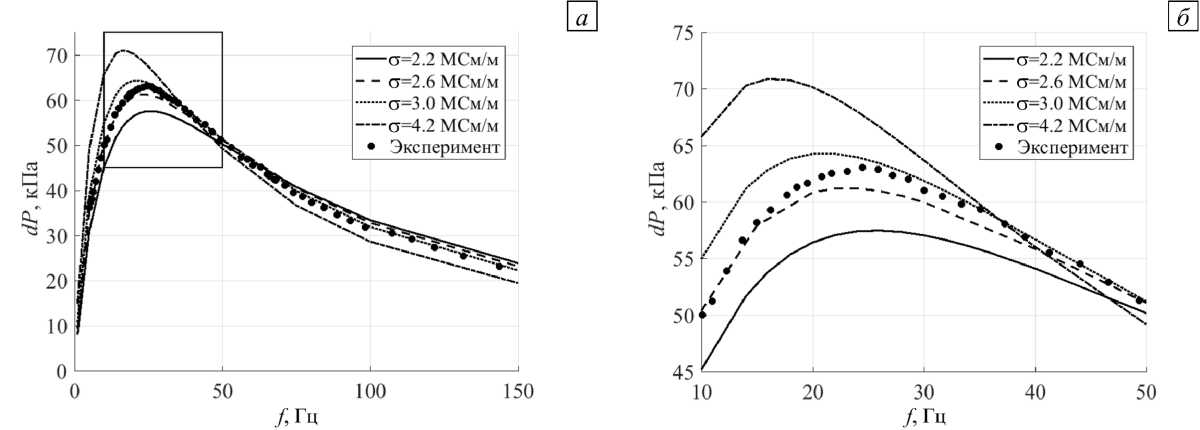
Рис. 5. Стопорный режим: зависимости перепада давления от частоты тока для разных значений электропроводности ( а ); те же кривые на выделенном участке в увеличенном масштабе ( б )

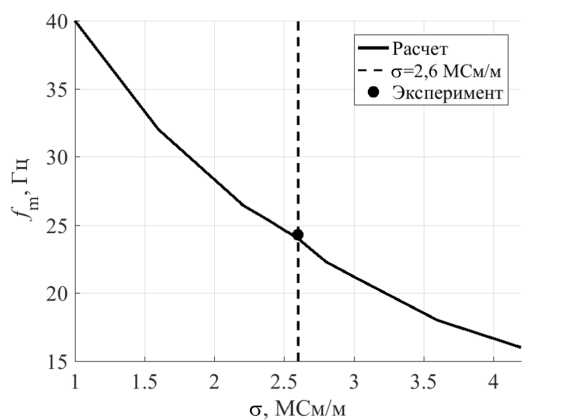
Рис. 6. Стопорный режим: зависимость частоты f _m , обеспечивающей максимум перепада давления на кривых рисунка 5, от электропроводности жидкого металла: расчет (сплошная линия), истинное значение электропроводности эвтектики 2.6 МCм/м (штриховая линия), эксперимент (точка)

расхода жидкого металла по контуру. Следует

Расходный режим, при котором в канале присутствует транзитное течение, созданное электромагнитным насосом, безусловно отличается от стопорного режима в аспекте поиска аналогичных зависимостей. Если в стопорном режиме удается исключить из описанного анализа две важных характеристики — вязкость и плотность, и сосредоточить внимание только на электропроводности, то в расходном режиме на вид зависимостей они будут влиять уже все. Тем не менее, для расходного режима проведено аналогичное исследование, но в этом случае в расчетах значение электропроводности фиксировалось, а менялась величина расхода транзитного течения. Некоторые из полученных расчетных зависимостей изображены на рисунке 7.

В эксперименте зависимость перепада давления от частоты определялась точно таким же образом, как и в рассмотренном ранее стопорном режиме, но вентиль в ходе измерения открывался лишь настолько, чтобы обеспечивалось заданное значение отметить, что при этих условиях неизбежно отличие расчетных и экспериментальных значений перепада давления. Причина заключается в том, что в галлиевом контуре места измерения перепада давления располагаются на некотором удалении от концов канала. Между этими участками находятся подводящие трубопроводы, переходные конусы, сужения и расширения каналов. Все это вносит вклад в гидравлическое сопротивление, который не учитывался в расчетах из-за ограничения в вычислительных ресурсах. Таким образом, расчет в расходном режиме дает более высокие значения перепада давления, чем эксперимент. Поэтому на рисунке 7 зависимости перепада давления от частоты нормированы на максимальное значение. Графики, построенные по данным расчета и эксперимента, имеют похожий вид, а основное отличие наблюдается в области высоких частот. Однако это не представляет проблемы, так как экстремумы расположены в области низких частот.

Эксперименты по измерению зависимостей перепада давления от частоты удалось провести только для относительно небольших расходов, поэтому на рисунке 7 не видны различия в положении максимума перепада давления для трех разных расходов. Этот же факт подтверждает и рисунок 8, на котором отражены зависимости величины частоты fm , обеспечивающей экстремум перепада давления, от расхода жидкого металла. Тем не менее, отличие расчетных и экспериментальных результатов на рисунке 8 имеется, но оно является небольшим. Расчеты показали, что при увеличении расхода существенно увеличивается частота fm (Рис. 8), что также хорошо видно на рисунке 7б. Однако при больших расходах нельзя утверждать, что на положение максимума влияет только значение электропроводности из-за возрастающего влияния гидросопротивления, которое зависит в том числе от плотности и вязкости. Небольшое изменение частоты fm при малом расходе (Рис. 8), когда вклад гидросопротивления в общий перепад давления незначителен, дает надежду на возможность реализации методики определения электропроводности даже в режиме с транзитным течением, что имеет свои преимущества перед реализацией этой методики в стопорным режиме.

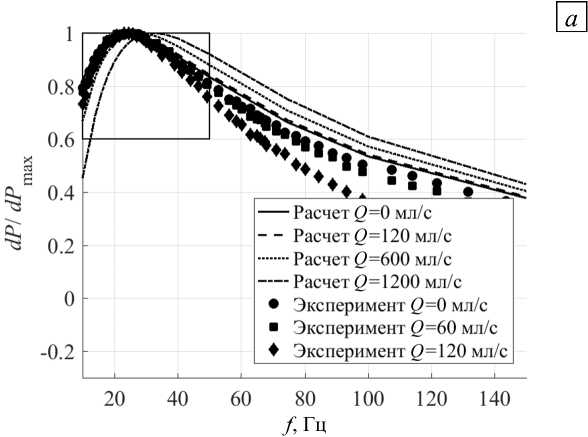
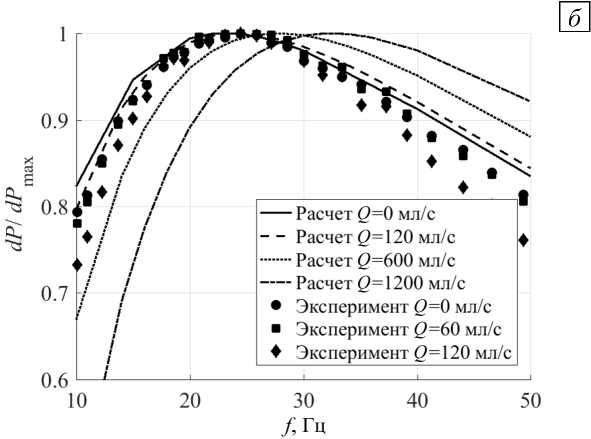
Рис. 7. Расходный режим: зависимости перепада давления от расхода для разных значений электропроводности ( а ); те же кривые на выделенном участке в увеличенном масштабе ( б )

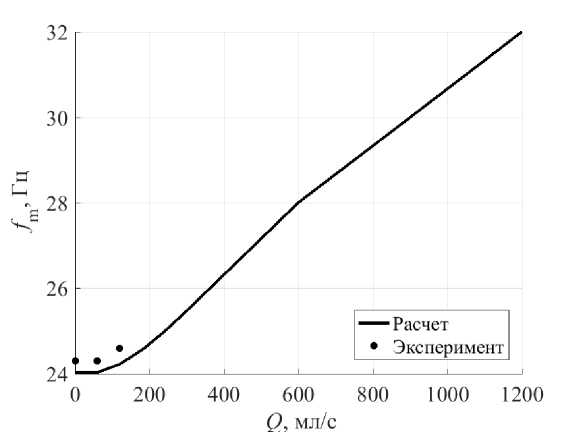
Рис. 8. Расходный режим: зависимость частоты f _m , обеспечивающей максимум перепада давления на кривых рисунка 7 от расхода жидкого металла: расчет (сплошная линия) и эксперимент (точки)

При оценке значения коэффициента полезного действия (КПД) электромагнитного насоса следует учитывать, что для апробированных в эксперименте расходов оптимальное значение частоты питающего тока меняется незначительно (Рис. 7, 8). Следовательно, потребление электрической энергии также мало зависит от расхода электропроводящей среды. В свою очередь значение частоты, которое обеспечивает максимальную производительность электромагнитного насоса (гидравлическую мощность), близко к значению этой частоты в стопорном режиме (24.4 Гц). Как известно, гидравлическая мощность есть произведение расхода на перепад давления. Эксперименты показали, что при токе 7.5 А максимальная достигнутая гидравлическая мощность составила 6.2 Вт (156 мл/с при перепаде давления 39.3 кПа), при этом полная потребляемая электрическая мощность оказалась равной 1.5 кВт. Активная мощность в эксперименте не измерялась, но обычно ее значение существенно меньше полной (более чем в два раза). Это обусловлено высоким индуктивным сопротивлением насоса, которое приводит к появлению сдвига фаз между током и напряжением. Поэтому в эксперименте при расходных режимах значение КПД не превышало 5% и практически не изменялось. Обычно КПД электромагнитных насосов подобного типа, например, для натрия, не превышает 15%. Малое значение КПД в данном исследовании обусловлено малой электропроводностью галлиевой эвтектики по сравнению с электропроводностью чистого натрия.

4.    Заключение

Основным результатом исследования является обнаружение существования экстремума на зависимости перепада давления между входом и выходом канала электромагнитного насоса от частоты электрического тока, питающего обмотки индуктора при фиксированном значении силы тока. Наличие экстремума подтверждено как в численном, так и в экспериментальном исследовании электромагнитного насоса при одних и тех же физических и геометрических параметрах. Особую значимость имеет выявленная близость значений частоты, обеспечивающей максимум перепада давления в расчете и в эксперименте. Для подтверждения достоверности результатов математического моделирования, выполнена верификация модели путем сопоставления результатов расчетов и экспериментов.

Факт наличия экстремума важен с практической точки зрения. Им можно воспользоваться для разработки методики измерения электропроводности расплавленной среды. Это подтверждается совпадением результатов расчета и эксперимента (см. точку на Рис. 6). Результаты расчета, полученные при значении электропроводности эвтектики оказались наиболее близкими к экспериментальному значению. Это объясняется тем, что в процессах с переменными магнитными полями определяющую роль играет величина произведения электропроводности на частоту переменного поля [3, 4, 10]. Поэтому, вследствие близости расчетных и экспериментальных данных, установленных при одинаковых значениях частоты, можно сделать вывод о близости значений электропроводности в расчете и эксперименте. Однако немаловажно, что это утверждение справедливо при умеренных значениях напряжения питания насоса, позволяющих оставаться в линейной области свойств ферромагнитных элементов конструкции [10].

Таким образом, методика определения значения электропроводности у расплава, чистота которого меняется в процессе его эксплуатации, может быть организована следующим образом. На участке трубопровода, в котором есть электромагнитный насос с известными геометрическими и техническими характеристиками, а также два цифровых манометра на входе и выходе канала насоса, должен быть вентиль, обеспечивающий частичное или полное перекрытие потока. Питание насоса должно осуществляться от частотного регулятора напряжения, а параметры насоса, а также показания манометров — выводиться на управляющий компьютер. При намерении произвести замер электропроводности необходимо вентилем перекрыть течение расплава, а затем последовательно устанавливать значения частот в некотором интервале и находить соответствующие им перепады давления. Далее построить зависимость «частота тока–перепад давления» и выделить частоту, обеспечивающую максимум перепада давления. После этого, на заранее рассчитанной для данного насоса зависимости экстремальной частоты от электропроводности, установить значение электропроводности.

Необходимо особенно подчеркнуть, что для использования описанной выше методики определения электропроводности нужна совокупность данных с измерительной техники и полученных путем математического моделирования. Без математического моделирования методику можно реализовать только после калибровки системы измерения на эталонном чистом металле. Причем такая калибровка должна проводиться с периодичностью, обусловленной требованиями к эксплуатации подобного рода систем. Осуществить же ее в условиях реального процесса в металлургической или энергетической промышленности невозможно. Причиной является неизбежное загрязнение металла или расплава в технологическом процессе, что приводит к неустранимым остаточным отложениям загрязнений в разных участках системы [2, 13]. Поэтому, даже после замены загрязненного жидкого металла новым чистым, эти отложения снова попадут в него и повлияют на его свойства. Следует отметить, что такие устройства, как электромагнитные насосы в гидравлических контурах, в течение многих лет эксплуатируются без возможности их изъятия для проведения регламентных работ и калибровки [12]. Поэтому наиболее рациональным решением является использование предлагаемой авторами методики, основанной на результатах математического моделирования и эксперименте процессов для выбранных конструкции электромагнитного насоса и расплава. Вследствие этого следует уделять повышенное внимание верификации математической модели на результатах лабораторных экспериментов с жидким металлом, свойства которого хорошо известны и стабильны [23, 27].

В этой связи выбор между конструктивными схемами, реализующими разные длины волн бегущего магнитного поля, может быть обусловлен стремлением получить наиболее острый пик на зависимости перепада давления от частоты (Рис. 4 б ). Исследования показали, что самый острый пик имеет место при наиболее длинной длине волны (при подключении по Типу 2). Дополнительным преимуществом является то, что в этой конфигурации достигается больший по величине перепад давления, чем в конфигурации с короткой волной (при подключении по Типу 1), что повышает чувствительность системы измерения. Поэтому, с одной стороны, можно рекомендовать использование конфигурации с наиболее длинной волной, с другой — для жидких металлов, обладающих большой электропроводностью (например для натрия) этот пик может оказаться слишком близко к области низких частот, где имеются аппаратные ограничения. Следовательно, для каждой конкретной задачи необходимо проводить дополнительное исследование по подбору длины волны.

Отдельного внимания заслуживают результаты, полученные в расходном режиме. В этом случае при осуществлении измерений жидкий металл продолжает протекать по каналу. Показано, что при относительно малых расходах значение частоты электрического тока, обеспечивающее максимум перепада давления, изменяется незначительно, а существенные перемены происходят при гораздо больших расходах (Рис. 8 б ). Поэтому описанную выше методику можно применять и при не полностью закрытом вентиле, то есть при расходном течении слабой интенсивности. При слабой интенсивности течения влияние вязкости и плотности на характер зависимости перепада давления от частоты будет незначительным. Вязкость и плотность среды могут повлиять только на гидравлическое сопротивление, которое при малых расходах дает несущественный вклад в общий перепад давления; последний почти полностью обусловлен электромагнитной силой. Разница уровней этих величин оценивается в два порядка. Следовательно, как и в стопорном режиме, положение на зависимости максимума давления от частоты будет определяться электропроводностью уже движущейся среды. Это особенно важно, когда в ходе производственного процесса нет возможности остановки транзитного течения, пусть даже на короткое время для проведения измерений или экспериментов, ввиду опасности нарушения технологии [2], [28], или перегрева металла. Тем не менее, и в таких условиях измерения производятся. В подобных случаях для поддержания стабильного расхода жидкого металла через канал процедура измерений усложняется. Организуется обратная связь между электромагнитным расходомером, который обязательно присутствует в подобных системах, и регулирующей арматурой.

Таким образом, результаты проведенного авторами исследования дают инструмент для оперативного контроля электропроводности расплавленного металла. Наиболее рационально данная методика может работать в системе очистки жидкого металла от примесей. Методика является полностью бесконтактной и использует те же аппараты, которые включаются в комплексы очистки, то есть не требует дополнительных устройств. В настоящее время методика апробируется в системе очистки жидкого натрия, который служит рабочей жидкостью в экспериментах, реализуемых в ИМСС УрО РАН.

Исследование выполнено за счет гранта Российского научного фонда и Пермского края № 22-19-20106,