Эквивалентные электрические модели биологических объектов

При прохождении переменного электрического тока через сложные структуры, в том числе биологические, наблюдается дисперсия электропроводимости, т.е. зависимость измеряемого сопротивления от частоты тока. Одним из критериев оценки состояния исследуемой среды является зависимость от частоты действительной и мнимой частей полного сопротивления, проводимости (адмиттанса) или комплексной диэлектрической проницаемости. Так как биологические ткани представляют собой сложные по составу гетерогенные среды, то они существенно различаются по электропроводным и диэлектрическим свойствам. Это обусловливает трудности измерения электрического сопротивления живых биологических тканей.

К настоящему времени разработано большое количество приборов и методов определения удельного сопротивления, проводимости и диэлектрической проницаемости. Было установлено, что величина биоэлектрического импеданса или адмиттанса существенно зависит от состояния тканей и кровообращения исследуемого участка тела человека. В [6, 8–10, 12] детально обсуждаются методы, приборы и схемы

Зуев Андрей Леонидович, д.ф.-м.н., старший научный сотрудник ИМСС УрО РАН, Пермь

Мишланов Виталий Юрьевич, д.м.н., заведующий кафедрой пропедевтики внутренних болезней ПГМА, Пермь

Судаков Андрей Иванович, старший научный сотрудник ИМСС УрО РАН, Пермь

Шакиров Нагим Вагизович, старший научный сотрудник ИМСС УрО РАН, Пермь

Фролов Александр Владимирович, д.б.н., заведующий лабораторией медицинских информационных технологий, Минск

О оз" 300

ш 280

ё 260

S 240

^ 200

10     100    1000   10000 100000 1000000

Частота, Гц

10    100   1000 10000 100000 1000000

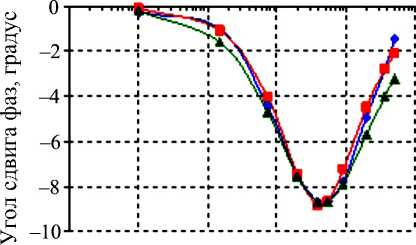
Частота, Гц б

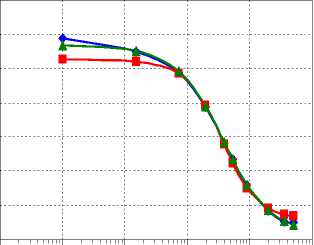
Рис. 1. Спектральные характеристики сегмента тела человека (отведение «правая рука – правая нога») [14]

а

для измерения импеданса; анализируются возможные методические и инструментальные погрешности измерения импеданса биообъектов и влияния на результат измерения применяемых методик и приборов, физических и химических процессов, протекающих в области контакта электродов и тканей.

Биоэлектрический импеданс представляет собой соотношение между напряжением и током, и поэтому для его моделирования используются электротехнические элементы и эквивалентные схемы замещения, под которыми понимаются модельные электрические схемы, составленные из резисторов, конденсаторов и более сложных структурных элементов. Построение эквивалентной схемы исследуемого объекта является важным этапом изучения данного физического явления. Модель должна не только отражать основные свойства биообъекта в исследуемой частотной и температурной областях, но и предсказывать поведение объекта в более широком диапазоне частот и температур. Правильность интерпретации результатов электрических измерений усложняется тем, что эквивалентные схемы замещения, как правило, неизвестны, и поэтому исследуемый объект с электродами и измерительной аппаратурой представляет собой «черный ящик». Достоверность реографических формул, устанавливающих количественную связь между характеристиками реограммы и гемодинамическими параметрами, существенно зависит от соответствия электрофизической модели реальному объекту [3, 4, 12, 13]. Примеры анализа спектров импеданса для некоторых биологических сред, электролитических материалов и композитов приводятся в [1, 6, 7, 9].

В настоящей работе обсуждаются известные эквивалентные схемы замещения и предлагаются их модификации для описания импеданса биологических сред. Устанавливаются условия тождественности некоторых эквивалентных схем замещения.

Эквивалентные схемы замещения и их диаграммы

Полное электрическое сопротивление объекта можно записать в виде комплексной величины: Z = Z ′ - iZ ′′ , где Z ′ – действительная (активная), Z ′′ – мнимая (реактивная) составляющие импеданса. Наглядным средством отображения частотных свойств биоимпеданса могут служить дисперсионная зависимость полного сопротивления Z и угла фазового сдвига ϕ = arctg ( Z ′′ / Z ′ ) тока и напряжения от частоты ω (рис. 1). Эта пара графиков называется диаграммой Боде.

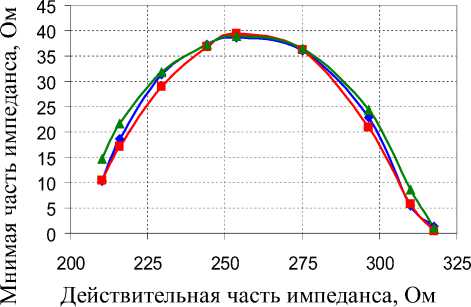
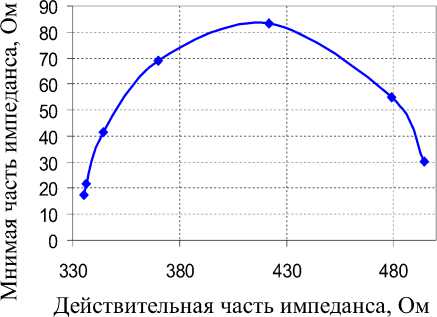
Другим наглядным представлением импеданса является векторная диаграмма комплексного сопротивления (годограф, график Найквиста), показанная на рис. 2. Ромбиками обозначены данные экспериментальных измерений, проведенных на сегменте человека (отведение «запястье правой руки – щиколотка правой ноги»). Результаты, представленные на рис. 2, а , взяты из работы [14], а на рис. 2, б – из работы [5].

ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 1 (55): 110–120 111

а

б

а

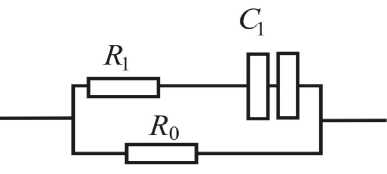
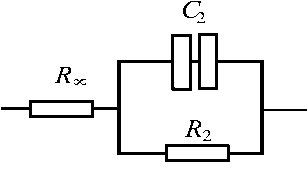
Рис. 3. Трехэлементные модели

Рис. 2. Диаграммы Найквиста для сегмента тела человека (отведение «правая рука – правая нога»)

б

Использование биоэлектрического импеданса для оценки состава тела значительно возросло в последние годы. Для качественного и количественного моделирования электрических свойств отдельных частей человеческого тела широко используется трехэлементная модель (рис. 3, а ), представляющая собой две параллельно включенные цепочки, одна из которых состоит из последовательно соединенных сопротивления R 1 и конденсатора C 1 , а другая – только из активного сопротивления R 0 . При низких частотах величина импеданса ( Z ) определяется сопротивлением межклеточной жидкости R 0 = ( Z ( ш^ 0 ) ) . С ростом частоты переменного тока реактивное сопротивление емкости ( C 1 ) уменьшается и все большая часть тока проходит внутри клеток. Используя правила расчета импедансов параллельного и последовательного соединения активного и реактивного элементов, для высоких частот находим R , = R 0 Z ( ш ^ w )/( R 0 - Z ( ш ^ да )).

Для эквивалентной схемы замещения, приведенной на рис. 3, а , величины импеданса и фазового угла легко вычисляются:

Z = R o + ( R o + R , ) R о R , C , ²®² - iR C , ® 1 + ( R 0 + R , )² C , ²®²

tg ф =

R 0 C , ш

1 + ( R 0 + R , ) R , C , ² ш ² "

Из формулы (2) следует, что фазовый угол при некоторой частоте ш = ш * достигает экстремума. Из условия экстремума фазового угла ф находим частоту, при которой отставание напряжения от тока максимальное:

ш* =  Ro - Z и

C , R о V R o Z ( да )"

Выделяя в формуле (1) активную ( Z ’ ) и реактивную ( Z" ) составляющие импеданса, а затем исключая частоту го , получаем в комплексной плоскости ( Z’ , Z ") уравнение окружности:

Z ‘

—

^+ Z ( » ) Y ₊₍ Z ,) 2 = ( R o — Z ( да ) ) ²

2 J              V 2       )

.

Уравнение (4) описывает полуокружность с центром, лежащим на оси Z ‘ в точке, отстоящей от начала координат на расстоянии ( R ₀ + Z ( да ))/2, и радиусом, равным ( R ₀ — Z ( да )) / 2. Если в эквивалентной схеме, изображенной на рис. 3, б , сопротивления R ₂ и R «> выбрать равными: R ₂ = A R = ( Z ( го^ 0 ) — R _да ) , R _да= ( Z ( го ^ да ) ) , то годографом этой схемы будет полуокружность, также описываемая уравнением (4). Экстремум тангенса фазового угла для данной модели достигается при частоте

*го

R 0

C 2 ( R o — Z ( да )) ,№'

Из сравнения формул (3) и (5) следует необходимое условие тождественности трехэлементных моделей, приведенных на рис. 3:

C 1

C 2

(

V

—

R

да

R 0

Таким образом, зная экстремальную частоту го *, начальное Z (0) и конечное Z ( да ) значения импеданса, можно легко найти параметры ( R ₀ , R _ю , R i , R ₂ , C ₁ , C ₂ ) трехэлементных эквивалентных схем замещения. Диаграммы Боде и Найквиста этих трехпараметрических моделей совпадут, если емкости выбрать удовлетворяющими соотношению (6).

Диаграммы Найквиста для многих биообъектов представляют собой «сдавленную полуокружность» (окружность с центром, лежащим ниже оси Z ‘ ) [6, 14] или результат перекрытия нескольких полуокружностей [1, 10]. Смещение центра окружности с горизонтальной оси легко достигается, если в эквивалентных схемах, изображенных на рис. 3, конденсаторы заменить на элемент постоянной фазы « Constant Phase Element – CPE » (рис. 4), импеданс которого задается формулой [11]

Z = A (i гот)—а, (7)

где A - фактор пропорциональности; т - постоянная времени, определяющая характеристическую частоту модели; а - безразмерный параметр.

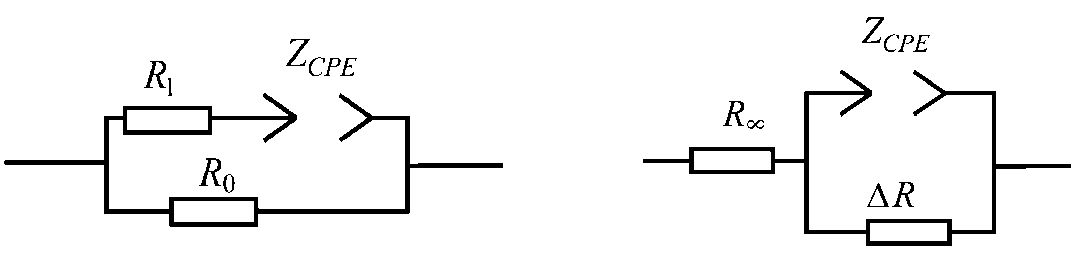
а                                       б

Рис. 4. Эквивалентные модели Коула–Коула

CPE представляет собой довольно простой структурный элемент, но вместе с тем обладает высокой обобщенностью. Импедансные диаграммы элемента постоянной фазы в зависимости от фактора n анализируются в [1]. В частности, для a = 1 элемент CPE вырождается в конденсатор.

На примере модели Коула–Коула, представленной на рис. 4, б , продемонстрируем схему построения диаграмм Боде и Найквиста и результаты сравнения экспериментальных и расчетных данных.

Используя правило расчета импедансов последовательного и параллельного соединений структурных элементов электрической схемы, показанных на рис. 4, б , получаем для импеданса, угла сдвига фаз и экстремальной частоты следующие выражения:

( R 0 - R то ) 1 ⁺ ( ^штГ ^cos I ^a

Z = R ■

1 .               ^a _ _ _ I _ ^п I . / _\^2a

1 + 2 (шт) cos I a—1 + (шт)

^a I

(тш) sin I a

tg ф =

-

R о + ( ^тш ) “

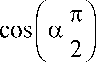
2 a

(Ro + R J + RДтЮ)2“

^(ш * ^т)

На рис. 1 представлены результаты сравнения экспериментальных [14] (отмечены ромбиками) и расчетных данных (показаны квадратиками), выполненных по формулам (8)-(10) при следующих параметрах: R 0 = 305,3 Ом; R _ю = 211,4 Ом; a = 0,89; т= 4,8^10 6 с.

На этом же рисунке треугольниками показана аппроксимация, выполненная с использованием модели, изображенной на рис. 6, а. При этом значения параметров модели принимались равными: R 1 = 973 Ом; R 2 = 227 Ом; R 3 = 307 Ом; C 1 = 2,217·10^–9 Ф; C 2 = 4·10^–9 Ф. Так как последняя модель содержит два конденсатора, то можно ввести в рассмотрение два времени релаксации (см. приложение) и найти их отношение:

X 1 = R 1 C 1 = 2,1^10 ⁶ с, X ₂ = R ₂ C ₂ = 9^10 5 с, X , / X ₂ = 2,3. (11)

Заметим, что для данного биологического объекта времена релаксации оказались одного порядка и сопоставимыми с постоянной времени т , входящей в модель Коула–Коула. Для того чтобы построить годограф Найквиста, выделим в формуле (8) действительную и мнимую части:

Z '- R

то

1 + 2 (toT)a

Z ''

( R 0 ^{- R} то ) ^{1 1} ( ^шт ) ” ^cos

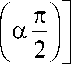
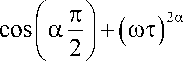
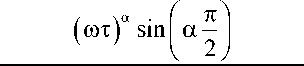
1 , / _\ a___l_nl./ _\2 a

1 + 2 (шт) cos I a— 1 + (шт)

и найдем их отношение

Z '- R _w z "

I n + ctg I a

(ютГ

• I n sin a —

I 2

Подставляя угловую частоту, выраженную из уравнения (14), в соотношение (13), после несложных преобразований получим уравнение окружности с центром, лежащим ниже действительной оси:

Z'

—

R о + R , Y

2 J

+ Z" к

A R

—

2 ctg

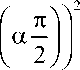
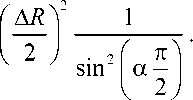
Если в качестве электрической схемы выбрать модель, представленную на рис. 4, а , а сопротивление R 1 принять равным R 0 R „/ ( R 0 — R „ ) , то ее импедансные характеристики (модуль импеданса, угол сдвига фаз и экстремальная частота) совпадут с результатами вычислений, выполненных по формулам (8)–(10). Заметим, что уравнение окружности (4) и условие экстремальности фазового угла (5) непосредственно следуют из соотношений (15) и (10) при a = 1.

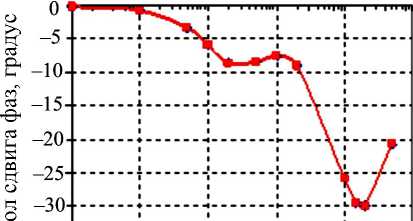
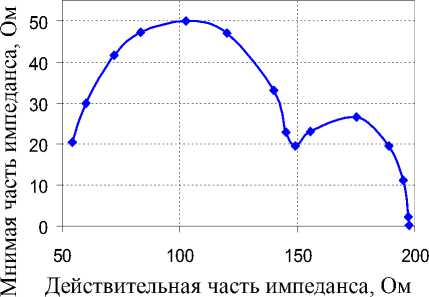
Импеданс многих биообъектов не описывается трех- или четырехэлементными схемами, рассмотренными выше; их годограф Найквиста отличается от окружности, а диаграмма фазового угла характеризуется несколькими экстремумами. Это хорошо иллюстрируют экспериментальные данные реограммы легкого [10], приведенные на рис. 5. Следует отметить два четко выраженных экстремума на диаграмме фазового угла (см. рис. 5, а ) и пересечения окружностей, имеющих различные диаметры и места расположения их центров (см. рис. 5, б ).

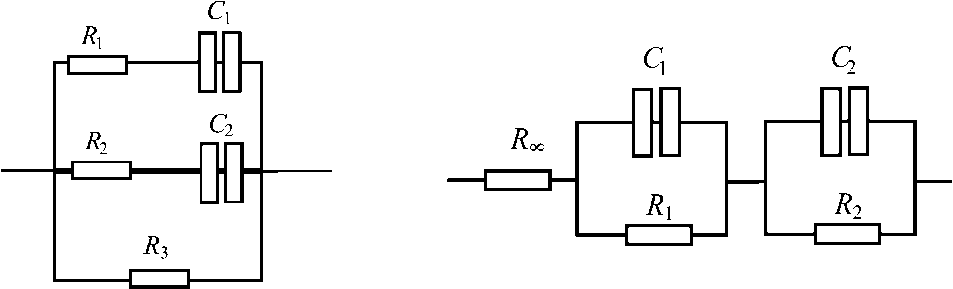
В работе [10] для расчета импеданса использовалась пятиэлементная модель, приведенная на рис. 6, б. Значения параметров, входящих в эту модель, принимались равными: R 1 = 49,7 Ом; R 2 = 97,9 Ом; R ∞ = 49,8 Ом; C 1 = 1,44·10^–7 Ф; C 2 = 1,47·10^–9 Ф. Вычислим для этой модели времена релаксации и их отношение:

X , = R 1 C 1 = 71,57-10 7 с, X ₂ = R ₂ C ₂ = 1,44-10 7 с, Х 1 / X ₂ = 50.          (16)

Хорошая аппроксимация этих экспериментальных данных также достигается, если использовать модель, приведенную на рис. 6, а ( R 1 = 74,6 Ом; R 2 = 609 Ом; R 3 = 194 Ом; C 1 = 6,6·10^–9 Ф; C 2 = 8,8·10^–8 Ф). Для этой модели соответствующие времена релаксации, обозначенные как L 1 и L 2 , оказались равными

L 1 = 706,6-10 7 с, L 2 = 17,73-10 7 с, L 1 / L ₂ = 40. (17)

10    100   1000 10000 100000 1000000

> -35

Частота, Гц

б

Рис. 5. Спектральные характеристики легочной ткани человека

а

а                                      б

Рис. 6. Эквивалентные пятиэлементные модели

Частота, Гц а

Частота, Гц б

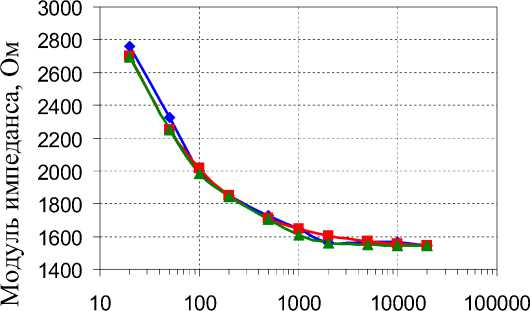
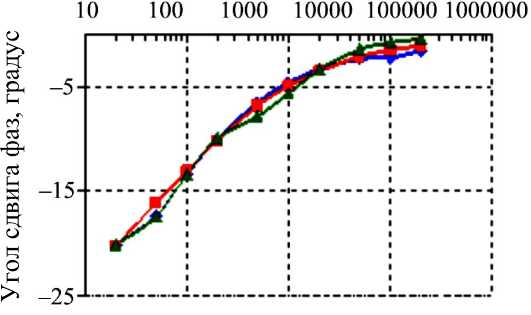
Рис. 7. Частотные зависимости реограммы человеческой крови

а                                       б

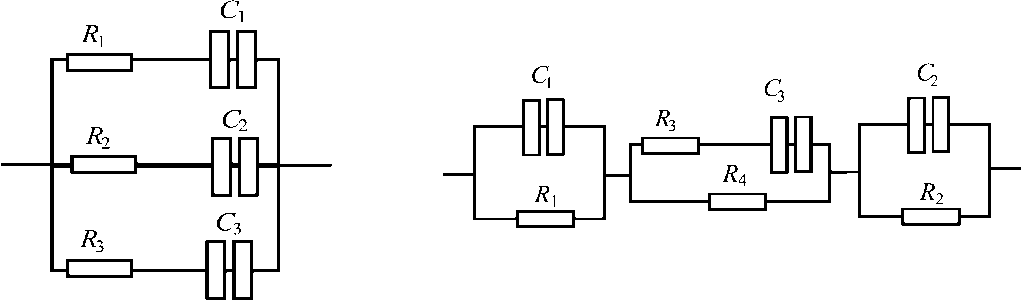
Рис. 8. Эквивалентные шестиэлементные и семиэлементные модели

Частотные зависимости биологических растворов и крови [3] отличаются от вышерассмотренных тем, что дисперсия импеданса наблюдается при значительно меньших частотах (рис. 7).

Такое поведение биологических тканей можно достаточно хорошо описать эквивалентными моделями, приведенными на рис. 8. Эти эквивалентные схемы обобщают соответствующие модели, приведенные на рис. 6. Как частный случай из модели, приведенной на рис. 8, б , при стремлении R 4 к бесконечности вытекает шестиэлементная эквивалентная схема, предлагаемая в работе [2] для описания импеданса крови.

Результаты вычислений, выполненных с использованием шестиэлементной модели (значения параметров: R 1 = 4148,7 Ом; R 2 = 8041,7 Ом; R 3 = 3972,2 Ом; C 1 = 1,18·10^–6 Ф; C 2 = 7,57·10^–8 Ф; C 3 = 1 Ф), показаны на рис. 7 треугольниками. Аппроксимация реограммы человеческой крови семипараметрической моделью ( R 1 = 170 Ом; R 2 = 170 Ом; R 3 = 2840 Ом; R 4 = 3610 Ом; C 1 = 3,1·10^–6 Ф; C 2 = 3,1·10^–6 Ф; C 3 = 1,46·10^–6 Ф) показана квадратиками.

116 ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 1 (55): 110–120

Параметры, входящие в эквивалентные схемы, находились из условия минимизации средней квадратичной погрешности. Отклонения расчетных реограмм от экспериментальных составляли не более 10%.

Обсуждение результатов

Если диаграмма Найквиста исследуемой биоткани представляет собой окружность (или кривую, близкую к ней) с центром, находящимся на действительной оси, то такую среду можно удовлетворительно моделировать эквивалентной схемой замещения, состоящей из двух сопротивлений и одного конденсатора (рис. 3). При этом значения сопротивлений находятся из условий R 0 = ( Z ( го^ 0 ) ) и R ^ = ( Z ( ю^” ) ) , а величина емкости – из условия максимального отставания напряжения от тока, т.е. параметры трехэлементной электрической схемы могут быть найдены без аппроксимации спектральных функций во всем частотном диапазоне.

Если центр окружности на диаграмме Найквиста находится ниже действительной оси, то спектральные характеристики объекта достаточно хорошо описываются моделью Коула–Коула или пятиэлементной электрической схемой. Из рис. 1 видно, что кривые Z = Z ( го ) и ф = ф ( го ) удовлетворительно описываются как моделью Коула–Коула, так и пятипараметрической электрической схемой, представленной на рис. 6, а . Следует отметить, что в модель Коула–Коула не входит в явном виде элемент, моделирующий емкостные свойства среды. Однако если задать а = 1, то элемент CPE вырождается в конденсатор с емкостью C , а параметр т становится равным произведению A R C . Следовательно, в данном случае постоянная времени совпадает с временем релаксации.

Поскольку модели, представленные на рис. 6, содержат по два конденсатора, то можно ввести в рассмотрение несколько времен релаксации. В том случае, когда отношение времен релаксации меньше 10, на частотной зависимости фазового угла имеется только один минимум (см. формулу (11) и рис. 1, б ).

Если времена релаксации электрической схемы отличаются в десятки раз, то кривая зависимости угла сдвига фаз от частоты имеет два минимума, а диаграмма Найквиста состоит из двух пересекающихся окружностей (см. формулу (17) и рис. 5).

Из рис. 5 видно, что обе модели предсказывают два экстремума на зависимости угла сдвига фаз от частоты. Из полученных выше значений времен релаксации можно предположить, что необходимым условием нескольких экстремумов на частотной зависимости угла сдвига фаз является отличие времен релаксации в десятки раз (см. формулы (16) и (17)).

Из вышеприведенных рисунков (см. рис. 1, б и рис. 5, а ) видно, что спектральные характеристики сегментов тела человека слабо изменяются вплоть до частот порядка 1000 Гц.

Выводы

Спектральные характеристики отдельных сегментов тела человека очень слабо изменяются вплоть до частот порядка 1000 Гц. Дисперсия же импеданса крови человека наблюдается при значительно меньших частотах.

Показано, что параметры электрической модели биологического объекта, эквивалентная схема которого содержит два сопротивления и конденсатор, могут быть найдены аналитически, если известны максимальное и минимальное сопротивления и значение экстремальной частоты на диаграмме угла сдвига фаз.

Сформулировано условие тождественности трехпараметрических электрических схем: одна из них представляет собой параллельную цепь R 2 C 2 с добавочным резистором R ∞ , а вторая – последовательную цепь R 1 C 1 , зашунтированную резистором R 0 .

Установлено, что необходимым условием появления двух экстремумов на частотной зависимости фазового угла (или представление диаграммы Найквиста двумя пересекающимися окружностями) является отличие времен релаксации эквивалентной схемы более чем в десять раз.

Приложение

На примере параллельной схемы замещения вычислим импеданс.

При параллельном соединении электрических элементов полный ток представляет собой сумму парциальных токов. Следовательно, для цепи, представленной на рис. П1, складываются обратные величины активного и емкостного сопротивлений:

и

U + CU = J ,                              (I)

R где U - напряжение; J - ток, J = Q, Q - электрический заряд.

Найдем решения уравнения (I) для двух конкретных изменений силы тока. В первом случае задается постоянный электрический заряд емкости Q = Q 0 (т.е. J = 0) и находится изменение напряжения во времени

U = —exp ^f— - 1 , C I xj

(II)

где λ – параметр, характеризующий скорость приближения напряжения к равновесному состоянию, λ = R · C . Уравнение (II) описывает релаксационный процесс, и поэтому параметр λ часто называют временем релаксации.

Во втором случае в правую часть уравнения (I) подставляется периодическая функция J = J 0 exp ( i ro t ) и находится периодическое решение

U =

R (1 - iroRC) 1 + (ro RC )2

J ₀exp ( i ro t ) .

Разделив напряжение на ток, находим изменение импеданса Z в зависимости от частоты:

R (1 — iroX) 1 + (roX)2

(III)

Параметр X имеет размерность времени. Размерность времени имеет и параметр т , входящий в выражение для импеданса элемента постоянной фазы (см. формулу (7)).

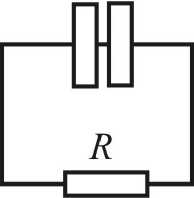
Рис. П1. Двухэлементная параллельная схема замещения

Покажем, что в случае а = 1 эти параметры совпадают. Если в модели, приведенной на рис. 4, б , сопротивление R ∞ выбрать равным нулю, то из формулы (8) находим

Z =

R0 (1 - iют)

1 + (ют)2

(IV)

Из сравнения формул (III) и (IV) видно, что сопротивление R0 = R, а постоянная времени т равна произведению RC (времени релаксации). Из формул (III) и (IV)

следует,

.

что параметры X и т определяют характеристическую частоту ю =--- RC

То есть существенное изменение импеданса и фазового угла начинается лишь при частотах, превышающих ю.

Благодарности

Работа поддержана Российским фондом фундаментальных исследований (проекты РФФИ-Урал № 11-08-96005 и № 11-04-96017).