Эквивалентные параметры круглой однородной мембраны
Бесплатный доступ
Кратко рассмотрена существующая методика определения эквивалентных параметров круглой однородной мембраны. Проанализирован недавно предложенный (в 2013 г.) новый подход к проблеме определения эквивалентных параметров круглой однородной мембраны. В рамках этого подхода параметры эквивалентного поршня определяются из условия тождественности законов движения при вынужденных колебаниях «усредненной» мембраны и эквивалентного поршня того же диаметра, помещенного на место мембраны, т.е. в тех же условиях возбуждения. Параметры эквивалентного поршня оказываются при этом зависящими от частоты возбуждения (кроме массы поршня). Введение дополнительного условия равенства средней за период кинетической энергии поршня и мембраны позволяет однозначно определить массу эквивалентного поршня, которая также становится частотно зависимым параметром. Аналогичные действия с потенциальной энергией поршня и мембраны позволяют определить параметр жесткости эквивалентного поршня другим способом. Сравнение этих результатов с помощью расчета показывает их полное совпадение. Произведено сопоставление нового метода со старым методом упрощенного расчета акустических систем, включающих мембраны. Расчетные формулы проиллюстрированы графиками, построенными для реальной мембраны. Приведены примеры расчета акустических колебательных систем, включающих круглую мембрану. Учтены поправки, связанные с излучением звука мембраной, совершающей колебания под действиемвынуждающейсилы
Круглая мембрана, эквивалентные параметры, вынужденные колебания, кинетическая энергия мембраны, потенциальная энергия мембраны, акустическая колебательная система, излучение мембраны, барабан
Короткий адрес: https://sciup.org/14316185
IDR: 14316185
Текст научной статьи Эквивалентные параметры круглой однородной мембраны
Электронный журнал «Техническая акустика»
В начале XX века, когда появилась необходимость в расчете электроакустических устройств, содержащих круглые однородные мембраны, исследователи пошли по пути упрощения этих расчетов с помощью замены системы с распределенными параметрами (мембрана) эквивалентной системой с сосредоточенными параметрами. В качестве таковой использовался линейный осциллятор (система груз–пружина), массовым элементом которого является плоский круглый поршень той же площади, что и рассматриваемая мембрана. Параметры эквивалентной системы называются эквивалентными параметрами замещающей системы (осциллятора).
Дальнейший расчет содержащей мембрану акустической системы производился уже с участием заменяющего мембрану поршня. Это существенно упрощало расчет, позволяя избегать решения интегро-дифференциальных уравнений.
Для нахождения эквивалентных параметров использовался энергетический метод [1]. Кратко опишем его.
Отклонение точек мембраны от положения равновесия под действием статического равномерно распределенного по площади мембраны давления P описывается (для малых отклонений) дифференциальным уравнением:
' d 2 и 1 du Л
—2" +---
( dr r dr J
- P ,
(1.1)
где и = и (r) — поперечное отклонение кольцевого элемента мембраны радиуса r в направлении оси и, T — напряжение в сечении мембраны, P — величина статического давления. Сила давления действует в направлении, совпадающем с направлением оси и . Параметр T считаем константой, не зависящей от r .
Решение этого уравнения, удовлетворяющее граничным условиям (закрепление мембраны по круговому контуру), запишется в виде:
и ( r ) = и 0 P
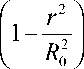
(2.2)
_ PR о 2 где и^р
0 P 4 т
— отклонение центра мембраны, R 0
радиус мембраны.
Пусть теперь P меняется по гармоническому закону. Амплитудное значение отклонения центра мембраны обозначим через и 0. Если предположить, что параболоидальная осесимметричная форма смещения (см. (1.2)) сохраняется при колебаниях на частоте основного тона колебаний мембраны, мы можем определить амплитудное значение кинетической энергии мембраны, суммируя энергии всех ее кольцевых элементов (выражение (1.3)).
При амплитуде колебаний поршня, равной и0 , равенство кинетической энергии мембраны и поршня обеспечивается при массе поршня mp, равной одной трети полной массы мембраны mm:
E kin
1 ( 1 n2 1 2
2 [ 3 ^^ m R 0 I и 0 ,
(3.3)
(4.4)
Потенциальная энергия мембраны может быть вычислена по работе, произведенной при ее растягивании [1]. Амплитудное значение потенциальной энергии мембраны:
E pot = ^ T^.
(5.5)
Приравнивая потенциальную энергию мембраны и потенциальную энергию поршня
(пружины), равную 2 kpu 02 , определим жесткость пружины осциллятора kp :
kp = 2 n T .
(6.6)
Частота основного тона мембраны определяется резонансной частотой осциллятора:
k p 6 T 2,449 T
(7.7)
a0 = —= ---т =---- —
V m p pPmR о R о pPm
Это выражение дает значение частоты, всего на 2 % отличающееся от точного значения частоты, определяемого последовательной теорией мембран:
^ 0
2,405 R 0
(8.8)
Благодаря столь высокой точности, приближенная формула (1.7) и ее вывод получили широкое распространение и вошли во многие известные книги по акустике.
Позднее стали учитывать не только равенство энергий мембраны и замещающего ее эквивалентного поршня (кинетической и потенциальной), но и равенство объемов воздуха, вытесняемого при движении мембраны и замещающего ее поршня [2]. Это нужно для сохранения воздействия на окружающую среду при переходе от мембраны к замещающей системе. Другими словами, объем воздуха, вытесняемый при колебаниях поршня, не должен отличаться от объема, вытесняемого при колебаниях мембраны [2]. (Площадь поршня по-прежнему считаем равной площади мембраны.)
Как и ранее, считаем, что параболоидальная форма смещения (1.2) сохраняется при колебаниях на частоте основного тона мембраны. Вычисляя упомянутые выше объемы и приравнивая их, получим значение амплитуды колебаний эквивалентного поршня в этом случае [2]:
U p = uf- (9.9)
При этой амплитуде колебаний поршня ( u p = и 0/2 ) равенство кинетической энергии мембраны и поршня обеспечивается при массе поршня, равной 4/3 полной массы мембраны:
E kin = 2 1 3 P R O2 I и p , (10.10)
mp = 3 P R 0 = 3 m m . (11.11)
Потенциальная энергия мембраны осталась прежней (см. (1.5)). Приравниваем потенциальную энергию мембраны и потенциальную энергию поршня, равную 2 kpup:
E„nt = nTun 2 = — ku 2 = -k„u 0 2 .
pot 02 p p 8 p 0
Отсюда находим жесткость пружины осциллятора в рассматриваемом случае:
к p = 8 ~ T .
(12.12)
(13.13)
Частота основного тона мембраны, определяемая параметрами осциллятора в этом случае, естественно, осталась прежней:
^ 0
kk^ = 2,449 FT \ m p R о pPm .
(14.14)
Рассмотренный подход дает высокую точность определения частоты основного тона мембраны. Замещение мембраны поршнем позволяет с определенной точностью рассчитывать акустические системы, включающие мембраны (см. рис. 1 в разделе 2.3), однако верхняя граница частотного диапазона, который может быть рассмотрен, лишь немного превышает частоту основного тона мембраны. При рассмотрении вынужденных колебаний мембраны на частотах, существенно превышающих частоту основного тона, этот подход не может быть применен.
Мембраны имеют широкое распространение во многих отраслях техники и, являясь классическим объектом, продолжают привлекать внимание исследователей, как в качестве модельного объекта, так и в качестве конкретного технического устройства (см., например, [3, 4]). При этом мембраны, как правило, являются частью акустических колебательных систем. Разработка простого и эффективного метода расчета таких систем без ограничений по частоте колебаний представляется достаточно актуальной задачей.
Такой метод был разработан и описан в работе [5], где была построена замещающая мембрану система с сосредоточенными параметрами с одной степенью свободы (осциллятор), способная описывать акустические колебательные системы, включающие мембраны, при любых частотах возбуждения. При этом не было сделано никаких упрощающих приближений (кроме общепринятых), то есть задача решалась точно. Были учтены также диссипативные потери, имеющие место при колебаниях мембраны.
В этой статье несколько уточним постановку задачи, произведем сопоставление нового метода [5] со старым методом упрощенного расчета акустических систем, включающих мембраны, в рамках нового подхода рассмотрим энергетические соотношения в движении мембраны и заменяющего ее эквивалентного поршня и, наконец, рассмотрим некоторые особенности применения метода эквивалентного поршня для расчета акустических колебательных систем, содержащих мембраны.
-
2. НОВЫЙ ПОДХОД К ПРОБЛЕМЕ ОПРЕДЕЛЕНИЯ ЭКВИВАЛЕНТНЫХ ПАРАМЕТРОВ КРУГЛОЙ ОДНОРОДНОЙ МЕМБРАНЫ
-
2.1. Круглая мембрана в различных условиях возбуждения
-
В этом разделе дана постановка задачи, с некоторыми уточнениями по сравнению с [5].
Рассмотрим вынужденные колебания круглой закрепленной по контуру мембраны под действием приложенного к одной стороне мембраны равномерно распределенного по площади избыточного (звукового) давления, меняющегося по гармоническому закону с амплитудой p 0 . Другая сторона мембраны соприкасается с невозмущенной воздушной средой. (Такие условия возбуждения можно наглядно представить, если мембрану вставить в круглое отверстие тонкого бесконечно протяженного жесткого экрана, делящего пространство на две полусферы. Со стороны одной из полусфер (например, правой) на мембрану падает плоская звуковая волна, фронт которой совпадает с плоскостью экрана.) Учтем диссипативные потери (например, структурные потери), вводя в рассмотрение силы сопротивления движению элементов мембраны, которые, как обычно, будем считать пропорциональными скорости этих элементов. Однако, явления, связанные с излучением звука мембраной, совершающей вынужденные колебания в воздушной среде, пока рассматривать не будем, они будут рассмотрены в разделе 3. (Таким образом, на этом этапе мы рассматриваем колебания собственно мембраны, без учета влияния на нее прилегающей воздушной среды, то есть, как бы помещая мембрану в вакуум и воздействуя на нее некоторой силой, равномерно распределенной по площади мембраны и меняющейся по гармоническому закону.)
Такие условия возбуждения вызывают поперечные осесимметричные колебания рассматриваемой мембраны, которые описываются (для малых отклонений) дифференциальным уравнением в частных производных гиперболического типа [6]:
д 2 и д и _д д 2 и 1 д и
—г + rm T —2 + дГ дt ^дг r д r у
iat
= Р 0 e ,
(2.1)
где p m - поверхностная плотность материала мембраны, и = и ( r , t ) - поперечное отклонение кольцевого элемента мембраны радиуса r в момент времени t (положительным считаем отклонение в сторону правой полусферы), rm – коэффициент сопротивления, отнесенный к единице площади, T – напряжение в сечении мембраны, p 0 - амплитуда поверхностной плотности вынуждающей силы, a - круговая частота вынуждающей силы, i = V— 1 - мнимая единица. Параметры p m , r m и T считаем константами, не зависящими от r и t .
Граничное условие и условие ограниченности для функции и ( r , t ) , справедливые при любых t , записывается в виде:
u ( r , t )| r = R 0 = 0, I u ( r , t )1 < да (при r < R 0 ), (2.2)
где R 0 — радиус мембраны.
Для рассматриваемых нами установившихся колебаний начальные условия не требуются.
Решение уравнения (2.1) с граничными условиями (2.2) можем записать в виде (см. [5]):
u ( ' ■ t ) = P^ [ J^ - 1 1 ■ ' ’ (23)
k T L J 0 ( kR o ) _
Pm^ - irm Ю где k = J ——t—m— (параметр k имеет смысл постоянной распространения поперечной волны на поверхности мембраны), J0 — функции Бесселя первого рода нулевого порядка от комплексного аргумента.
Это выражение полностью определяет установившееся движение мембраны в условиях возбуждения.
Пусть теперь на мембрану со стороны правой полусферы действует равномерно распределенное по площади мембраны избыточное давление p 1 , меняющееся по гармоническому закону с амплитудой p 01 , а со стороны левой полусферы действует также равномерно распределенное по площади мембраны избыточное давление p 2 , меняющееся с той же частотой ю, но с амплитудой p 02 и со сдвигом по фазе " 12 по отношению к давлению p 1 . Тогда правую часть уравнения (2.1) можем записать в виде ( Р 10 - Р 20 e"' ) eia>‘ = Р 0 eia>‘ , где P 0 — комплексная амплитуда суммарного воздействия давлений p 1 и p 2 на мембрану. Решение уравнения (2.1) теперь запишется в виде:
^/ u ( r, t ) = kT
JoSkrL _ 1
J 0 ( kR 0 )
eicot
(2.4)
Разница между выражениями (2.3) и (2.4) состоит только в том, что в выражении (2.4) учитывается начальная фаза колебаний возмущающей силы, равная аргументу комплексной амплитуды p 0.
В дальнейшем мы будем пользоваться более общим выражением (2.4).
2.2. Сводка необходимых формул
Далее приведем формулы, полученные в [5], которые понадобятся нам в дальнейшем. В этих формулах учтен более общий подход, даваемый выражением (2.4).
Уравнение движения «усредненной» мембраны:
^^
umid (t) I 2'i’ k2T
2 J 1 ( kR 0 ) _ 1 e - kR J o ( kR o ) J ,
(2.5)
где J 1 ( kR 0 ) — функция Бесселя первого рода первого порядка.
Выражение (2.5) мы можем записать в виде umid ( t) = Umideiat , где
^/
U -. = — mid 2
k 2 T
2 J i ( kR o ) _ 1 kR 0 J 0 ( kR 0 )
— комплексная амплитуда колебаний «усредненной» мембраны.
Уравнение движения поршня в тех же условиях возбуждения:
mp x + rpx + kpx = p o Spe‘ M ,
(2.6)
(2.7)
где mp — масса поршня, rp — коэффициент сопротивления движению поршня, kp —
жесткость пружины осциллятора, x — отклонение поршня от положения равновесия (положительным считаем отклонение в сторону правой полусферы), Sp = n R0 — площадь поршня, равная площади мембраны.
Решение уравнения (2.7) для установившегося режима находится методом комплексных амплитуд [7] и записывается в виде:
x ( t ) =
~ о iat p 0 S p e
2 . kp _ mp a + irp a
(2.8)
Параметры эквивалентного поршня:
m p = P m S p , (2.9)
kp = mp a 2 + SpT Re < k
2 J 1 ( kR 0 )
1 kR 0 J 0 ( kR 0 )
(2.10)
SpT.
r p = —Im ( a
k 2
2 J i ( kR ) _ 1 kR 0 J 0 ( kR 0 )
(2.11)
где Re и Im — действительная и мнимая части комплексного числа, стоящего в фигурных скобках.
-
2.3. Сопоставление амплитудно-частотных характеристик эквивалентных поршней с параметрами, определяемыми по старой и новой методике
Для иллюстрации приведенных формул и сопоставления их с используемыми ранее приведем результаты расчетов движения эквивалентного поршня, заменяющего конкретную слабо натянутую мембрану, использованную в работе [5]. В данном случае рассматриваются колебания собственно мембраны под действием гармонически меняющегося односторонне приложенного внешнего давления. Параметры мембраны: p m =0.063 кг/м2, r m =5 кг/м2с, T =10 Н/м, R 0 =0.027 м. Амплитуда вынужденных колебаний эквивалентного поршня определяется модулем комплексной амплитуды X из уравнения (2.8):
X =
p0Sp kp - mp^2 + irprn
(2.12)
На рис. 1 сплошной линией показана зависимость амплитуды вынужденных колебаний эквивалентного поршня от частоты возбуждения f , рассчитанная с помощью формулы (2.12) после подстановки в нее параметров эквивалентного поршня, определенных по формулам (2.9) – (2.11), или, что то же самое, с помощью формулы (2.6) (это справедливо только при рассмотрении колебаний собственно мембраны). Расчет сделан для p 0 = p 0 =20 Па (120 дБ).
На этом же графике пунктирной линией показана зависимость от частоты f
(рассчитанная по той же формуле (2.12)) амплитуды колебаний поршня с параметрами, определенными по формулам (1.11) и (1.13) для той же мембраны в тех же условиях возбуждения. Параметр rp в (2.12) определен по формуле rp = 3 rmSp .
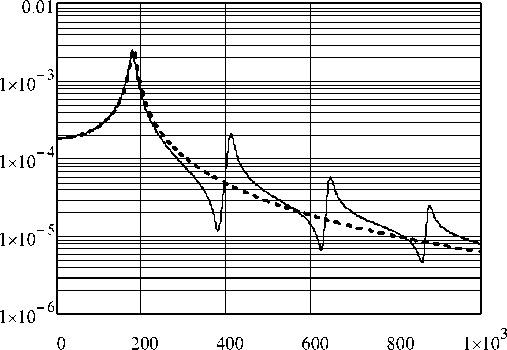
f, Hz
Рис. 1. Зависимость амплитуды колебаний эквивалентного поршня от частоты возбуждения, рассчитанная по новой (сплошная линия) и старой (пунктирная линия) методике. По оси абсцисс – частота в Гц, по оси ординат – амплитуда колебаний в метрах
Видим, что в окрестности первого резонанса и на более низких частотах кривые практически совпадают. Этот результат может быть получен математически.
Рассмотрим комплексную амплитуду Umd (см. формулу (0.6)). Если kR o| < 0, функции Бесселя J 0( kR 0) и J 1( kR 0) представимы в виде степенных рядов [1]:
J o ( kR 0 ) = 1 -
( kR o ) 2 + ( kR o ) 4
J , ( -R) =-y 1 -
( -R o ) 2 + 8
,
( kR 0 )4
.
Подставляем эти формулы в (2.6). При выполнении преобразований (деление, умножение многочленов), отбрасываем все члены со степенями k выше 4. В результате получим:
U mid
= PRL Г 1 + _±( -R )0 .
T
8 190
Подставляя сюда k из формулы (2.3), получим:
_ po R o 4 po Ro4 P,
-
4 p 0 R 0 4 r m
--o— a .
192 T 2
Umid =--'---, mid 8T 192
Далее рассмотрим формулу (2.12). Представим ее в виде:
X =
p o n R 02
.
m
r
mr kp 1 - a2 + i^p- a
k p
k p
Произведя аналогичные преобразования, получим:
p o n R o o p n m
k p
2 kp
a 0
p o n R 02 r p
2 kp
a .
Приравнивая свободные члены полученных выражений, можем определить kp : к p = 8 n T .
Приравнивая коэффициенты при одинаковых степенях а и учитывая полученное значение kp, определяем mp и rp : mp = 3 npmR2 , rp = 3 nrmRo2.
Полученные формулы совпадают с теми, что получены в разделе 1 (введение) с помощью энергетического метода (формулы (1.11) и (1.13)).
-
2.4. Определение массы эквивалентного поршня
Как отмечалось в [5], в рамках метода эквивалентного поршня определение массы эквивалентного поршня по формуле (2.9) является избыточным. Рассчитываемые величины смещений (или давлений) и фаз колебаний любых элементов акустических колебательных систем рассматриваемого типа от этого параметра не зависят. Это является следствием кинематического подхода к рассматриваемой проблеме. Такой подход в большинстве случаев является достаточным для описания акустических колебательных систем. Однако, при энергетическом подходе к решению задач (составление уравнения энергетического баланса, и, вообще, применение методов аналитической механики) нужно обеспечть не только кинематическую, но и энергетическую тождественность мембраны и заменяющего ее зквивалентного поршня. Это можно сделать с помощью параметра mp , который, как и другие параметры эквивалентного поршня, станет зависимым от частоты возбуждения.
Вернемся к осциллятору. Определим среднюю за период кинетическую энергию Ekin , p поршня осциллятора, уравнение движения которого описывается формулой
-
(2.7). Однако, с учетом того, что мы постулировали тождественность законов движения поршня и «усредненной» мембраны, можем воспользоваться выражением (2.5) для описания движения поршня:
x ( t ) = p 0 2 J i ( kR) k 2 T [ kR 0 J 0( kR 0 )
i „ iot
- 1 e .
(2.13)
Дифференцированием по времени выражения (2.13) определим скорость поршня x ( t ):
5c ( t ) =
i a p о 2 J i ( kR o ) , -1 e
iot
k 2 T [ kR 0 J0(kR 0)
(2.14)
которую запишем в виде: x ( t) = Xe a t , где
X = i a p 0 2 J i ( kR 0 )
k 2 T [ kR 0 J 0( kR 0 )
- 1
(2.15)
— комплексная амплитуда скорости движения поршня.
Вынужденные колебания поршня являются гармоническими, следовательно, средняя за период кинетическая энергия поршня равна половине от максимальной кинетической энергии, определяемой амплитудой скорости, которая, в свою очередь, определяется модулем комплексной амплитуды колебаний скорости X (см. формулу
(2.15)):
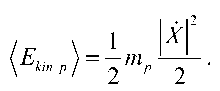
(2.16)
Аналогичным образом определим среднюю за период кинетическую энергию Ekin , m мембраны. Скорость кольцевого элемента радиуса r мембраны в каждый момент времени u i ( r , t ) определяется дифференцированием по времени выражения (2.4):
u ( r , t ) =
i a p 0 J 0 ( kr) - 1 ei<* k 2 T [ J 0( kR ) J .
(2.17)
Это выражение запишем в виде u ( r , t ) = U ( r ) е‘ш‘ , где
U ( r ) = i O p o k 2 T
J o ( kr ) - 1
J 0 ( kR 0 )
(2.18)
— комплексная амплитуда колебаний скорости кольцевого элемента мембраны радиуса r .
Каждый кольцевой элемент мембраны совершает вынужденные колебания со своей амплитудой и фазой. Скорость кольцевого элемента мембраны определяется амплитудой и фазой колебаний скорости, определяемыми комплексной амплитудой (2.18).
Определим среднюю за период кинетическую энергию dEkin , m кольцевого элемента мембраны радиуса r и толщины dr , пользуясь теми же рассуждениями, что и при записи формулы (2.16):
1 U ( r )
(dEn„» = —dm ' ------. (2.19)
kin , m 22
Средняя за период кинетическая энергия всей мембраны Ekin , m определяется интегралом:
R 0 2
(E* , m ) = - p m f | U ( r )| rdr . (2.20)
Массу эквивалентного поршня определим из условия равенства кинетической энергии мембраны и эквивалентного поршня, помещенного на место мембраны, то есть из равенства правых частей уравнений (2.16) и (2.20):
R 0 2
m p = тф f \U ( r ) rdr . (2.21)
X 0
Путем несложных преобразований с использованием тождества | z 1 z 2| = | z j | z 2|, где z 1 и z 2 — комплексные числа, выражение (2.21) можно привести к виду:
mp
2W m\ k 2| R o 02
12 J 1 ( kR o ) - kRJ o ( kR o)| 2
R 0 2
f | J o ( kr ) - J o ( kR o )|2 rdr .
(2.22)
Таким образом, параметры поршня, эквивалентного мембране по кинематическим и энергетическим характеристикам, определяются выражениями (2.22), (2.10) и (2.11). Параметр mp в выражении (2.10) определяется выражением (2.22).
В качестве иллюстрации на рис. 2 представлена зависимость массы эквивалентного поршня mp от частоты возбуждения f (Гц), рассчитанная по формуле (2.22) для той же мембраны, которая использовалась при построении графиков на рис. 1.
Пунктирной линией на графике показано значение массы эквивалентного поршня, вычисленное по формуле (1.11) для этой же мембраны. Видим, что значения массы эквивалентного поршня, вычисленные по формулам (1.11) и (2.22), на низких частотах (менее 100 Гц) практически совпадают.
На рис. 3 представлена зависимость жесткости эквивалентного поршня kp от частоты возбуждения f , рассчитанная по формуле (2.10) с учетом (2.22), для той же мембраны.
Пунктирной линией на графике показано значение жесткости эквивалентного поршня, вычисленное по формуле (1.13) для этой же мембраны. Видим, что значения жесткости эквивалентного поршня, вычисленные по формулам (1.13) и (2.10) с учетом (2.22), на низких частотах (менее 100 Гц) практически совпадают.
Вид приведенной на рис. 3 кривой существенно отличается от зависимости kp от f , рассчитанной для случая, когда масса поршня приравнивалась массе мембраны (график этой зависимости приведен в работе [5]).
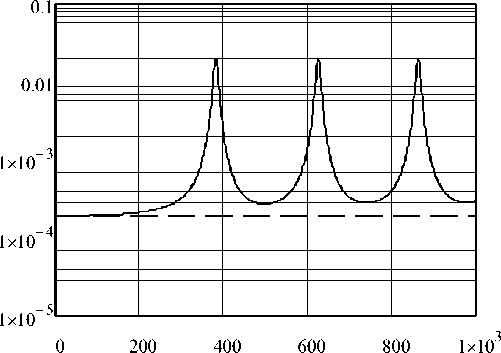
f, Hz
Рис. 2. Зависимость массы эквивалентного поршня mp (сплошная линия) от частоты возбуждения. По оси абсцисс — частота в Гц, по оси ординат — масса эквивалентного поршня в килограммах
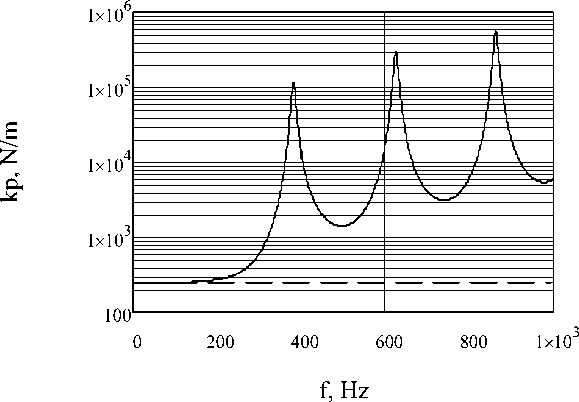
Рис. 3. Зависимость жесткости эквивалентного поршня kp (сплошная линия) от частоты возбуждения. По оси абсцисс — частота в Гц, по оси ординат — жесткость эквивалентного поршня в Н/м
-
2.5. Потенциальная энергия мембраны
Параметры эквивалентного поршня определены. Однако для полноты картины и для проверки полученных ранее формул определим параметр kp другим способом, из условия равенства потенциальной энергии мембраны и замещающего ее эквивалентного поршня.
Определим сначала потенциальную энергию мембраны. Вынужденные колебания мембраны описывается формулой (2.4). Перейдем к действительному значению отклонения кольцевого элемента мембраны радиуса r в момент времени t , которое обозначим как u = u ( r , t ) :
u ( r , t ) = Re[ u ( r , t )] = Re -
p 0 J o ( kr ) k 2 T [ J o ( kR o )
- 1
ei . (2.23) Потенциальная энергия, запасенная кольцевым элементом мембраны [2], может быть вычислена по формуле: dEpot, m(r , t) = nT flu 'l rdr . k dr I (2.24) Потенциальная энергия всей мембраны в момент времени t определяется интегралом: Ro fdu A2 Epot, m(t ) = ПТ j|-| rdr . (2.25) 0 k d r 1 Функция E pot,m (t) является периодической с частотой изменения, равной удвоенной частоте возбуждения. Средняя за период потенциальная энергия всей мембраны определяется по формуле: 1 TE (Epot,m ) = \ Epot,m (t)dt , (2.26) TE 0 где TE = — — период изменения потенциальной энергии мембраны в процессе 2f вынужденных колебаний, возбуждаемых с частотой f . Определим теперь потенциальную энергию эквивалентного поршня. Вынужденные колебания эквивалентного поршня описывается формулой (2.13), которую можно представить в виде x(t) = XeiCOt, где X = p 0 2 J1( kR)_ 1 (2.27) k2T [kR J0(kR) — комплексная амплитуда колебаний эквивалентного поршня. Вынужденные колебания поршня являются гармоническими, следовательно, средняя за период потенциальная энергия поршня равна половине от максимальной потенциальной энергии, определяемой жесткостью эквивалентного поршня и амплитудой колебаний, которая, в свою очередь, определяется модулем комплексной амплитуды колебаний X (см. формулу (2.27)): 1k X2. (2.28) 2p2 Приравнивая правые части уравнений (2.26) и (2.28), определяем kp : 4nT TE R0 kp T E d u Y j — I rdr dr ) dt (2.29) . Результаты расчета зависимости kp от частоты возбуждения f , сделанного по формуле (2.29) для использованной нами ранее мембраны (см. комментарии к рис. 1) полностью совпали с результатами расчета, сделанного по формуле (2.10) (в которой mp определяется по формуле (2.22)) и представленного на рис. 3 (сплошная линия). 3. ИСПОЛЬЗОВАНИЕ ЭКВИВАЛЕНТНЫХ ПАРАМЕТРОВ КРУГЛОЙ ОДНОРОДНОЙ МЕМБРАНЫ ДЛЯ РАСЧЕТА АКУСТИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ, СОДЕРЖАЩИХ МЕМБРАНЫ Применение эквивалентных параметров круглой однородной мембраны для расчета акустических колебательных систем, содержащих мембраны подробно описано в работе [5], где этот метод расчета назван методом эквивалентного поршня. Здесь остановимся только на некоторых особенностях метода. В этом разделе во всех случаях рассматривается мембрана, помещенная в воздушную среду. В виде поправок учитываются эффекты, связанные с излучением колеблющейся мембраной звука в окружающую среду. Если акустическая колебательная система такова, что мембрана окружена с обеих сторон полостями конечного объема V1 и V2 , мы ограничены только тем, что должны рассматривать вынужденные колебания элементов системы на частотах, при которых размеры этих полостей могли бы считаться малыми по сравнению с длиной звуковых волн, соответствующих этим частотам. В этом случае мембрана (или заменяющий ее эквивалентный поршень) может считаться ipc 2 S 2 Z =--- . Здесь p - плотность воздуха, °Veff вынуждающей силы, Veff – эффективный нагруженной на упругий импеданс [8] c - скорость звука, о - круговая частота объем, определяемый из соотношения — = — + —, где V и V - объемы первой и второй полости. Эффекты, связанные с Veff V1V2 излучением звука мембраной или поршнем здесь отсутствуют. Ограничение по частотам не позволяет нам рассматривать вынужденные колебания системы на частотах, соответствующих высоким осесимметричным модам колебаний мембраны. Однако при малых объемах V1 и V2 , малом натяжении мембраны и (или) большой поверхностной плотности материала мембраны могут быть рассмотрены относительно высокие осесимметричные моды. Если в системе имеется открытая мембрана, одна из сторон которой соприкасается с неограниченным или, по крайней мере, обширным воздушным пространством, возникает необходимость учета присоединенной массы, величина которой зависит от конфигурации окружающего мембрану воздушного пространства, в которое происходит излучение. Нужно также учесть потери энергии на излучение, которые также зависит от конфигурации окружающего мембрану воздушного пространства, в которое происходит излучение. Эти явления описываются с помощью механического импеданса излучения [8], который будет рассмотрен ниже. Рассмотрим вынужденные колебания круглой мембраны, вставленной в круглое отверстие тонкого бесконечно протяженного жесткого экрана, делящего пространство на два полупространства. Считаем, что возбуждение колебаний осуществляется тем же способом, который описан при выводе формулы (2.4). Теперь мы рассматриваем мембрану как акустическую колебательную систему, в полной мере взаимодействующую с прилегающей воздушной средой. Будем решать задачу в низкочастотном приближении, когда, хотя бы в первом приближении, справедлива замена излучающей мембраны излучающим плоским поршнем. Это возможно при рассмотрении вынужденных колебаний мембраны на частотах, при которых размер мембраны (диаметр) мог бы считаться малым по сравнению с длиной звуковых волн, соответствующих этим частотам. Активная и реактивная компоненты механического импеданса излучения круглого поршня в жестком экране (каждая сторона поршня излучает в открытое для нее полупространство) определяются с помощью функций Бесселя и Струве первого порядка [8]. Ряды, которыми могут быть представлены эти функции достаточно быстро сходятся при 2 — R00 меньшем единицы (или, что то же самое, при Л большем 4nR0, c это требование находится в согласии с тем, что описано в предыдущем абзаце) и для упрощенного анализа рассматриваемых эффектов можно ограничиться первыми членами этих рядов. Тогда компоненты импеданса могут быть записаны в следующем виде: Р—sp , (3.1) г =-----— rad ПС yrad = —mrad 116 pR03 —---- (3.2) Здесь rrad и yrad — действительная и мнимая части механического импеданса излучения поршня, двусторонне излучающего в две полусферы, mrad — присоединенная масса поршня. Воспользуемся методом эквивалентного поршня [5], в соответствии с которым запишем уравнение движения эквивалентного поршня в рассматриваемых условиях: (3.3) (mp + mrad )X + (rp + rrad )x + kpx = P0Spe— , где mp, rp, kp и Sp = nR02 — параметры эквивалентного поршня, определенные по формулам (2.9)—(2.11), x — отклонение поршня от положения равновесия (положительным считаем отклонение в сторону правой полусферы). Решение уравнения (3.3) для установившегося режима может быть найдено методом комплексных амплитуд [7] и после несложных преобразований записано в виде: x(t) = - ri „ —ft P 0 Spe SpTk2 2J1(kR0) kR0J0(kR0) T1 -1 -mrad — + irra— (3.4) Запишем эту формулу в виде x(t) = Xeiat, где X= p0Sp SpTk2 2J1(kR0) kR0J0(kR0) -1 -mrad^2+ irrad^ (3.5) — комплексная амплитуда колебаний эквивалентного поршня. Амплитуда колебаний эквивалентного поршня определяется модулем комплексной амплитуды X . На рис. 4 представлена зависимость амплитуды колебаний эквивалентного поршня X от частоты возбуждения f , рассчитанная по формуле (3.5) для рассмотренной выше (см. комментарии к рис. 1) мембраны в тех же условиях возбуждения. f, Hz Рис. 4. Зависимость амплитуды колебаний эквивалентного поршня без учета (пунктирная линия) и с учетом поправок на излучение (сплошная линия) от частоты возбуждения. По оси абсцисс — частота в Гц, по оси ординат — амплитуда колебаний эквивалентного поршня в метрах На рис. 4 мы видим, что учет поправок на излучение существенно сдвигает частоту первого резонанса мембраны в сторону уменьшения. Примерно такой же результат дает расчет радиационных поправок для значительно более сильно натянутых мембран. Анализ формулы (3.5) показывает, что определяющее влияние на изменение вида амплитудно-частотной характеристики поршня (поправки на излучение) оказывает величина присоединенной массы. Влияние активной компоненты импеданса излучения несущественно. В заключение кратко рассмотрим поправки на излучение для задачи о вынужденных колебаниях мембраны барабана [5]. Будем считать в этом случае, что эквивалентный поршень, заменяющий мембрану, односторонне излучает в открытое пространство (без экрана). В рамках тех же приближений, что и в предыдущей задаче, активная и реактивная компоненты механического импеданса излучения могут быть записаны в виде [8]: r rad p®2 sp , 4nc (3.6) Угол = mrad® = 2PR 0^. (3.7) Здесь rrad и yrad — действительная и мнимая части механического импеданса одностороннего излучения поршня в сферу, mrad — присоединенная масса поршня. Уравнение движения эквивалентного поршня для данной задачи запишется в виде: (mp + mrad )x + (rp + rrad )x + kp + Pc Sp V i®t x = p 0 Spe , (3.8) где mp, rp, kp и Sp = nR0 — параметры эквивалентного поршня, определенные по формулам (2.9)—(2.11), V — объем полости барабана. Решение уравнения (3.8), как обычно, находим методом комплексных амплитуд [7] и после несложных преобразований комплексную амплитуду колебаний эквивалентного поршня записываем в виде: X =--- SpTk2 2J1(kR0) kR0J0(kR0) p0Sp -1 PC 2 Sp 2 • + - mrad® + irrad® (3.9) Формула (3.9) определяет амплитуду и фазу вынужденных колебаний мембраны барабана на любой частоте возбуждения (в рамках рассматриваемого диапазона) и описывает эффекты, связанные с присоединением объема V и излучением мембраны. Новый подход не только расширяет частотный диапазон, но, благодаря тому, что используется точное решение задачи о колебаниях мембраны, он позволяет получать точные решения при расчете колебательных систем (а не приближенные, как в классическом методе). Параметры эквивалентного поршня, замещающего мембрану, оказываются при этом зависящими от частоты возбуждения. При условии кинематической идентичности мембраны (точнее, «усредненной» мембраны) и эквивалентного поршня частотно зависимыми параметрами становятся жесткость поршня (пружины осциллятора) и коэффициент сопротивления движению поршня. Масса поршня может оставаться неопределенной. Наложение дополнительного условия равенства средней за период кинетической энергии поршня и мембраны приводит к тому, что масса поршня также становится частотно зависимым параметром. Величина массы поршня при низких частотах совпадает с аналогичной величиной, вычисленной старым методом. Из условия равенства средней за период потенциальной энергии поршня и мембраны можно определить «жесткость» эквивалентного поршня другим способом. Сравнение выражений для определения kp, полученных разными способами, с помощью расчета показывает их полное совпадение. Приведенные в статье примеры применения метода показывают, что он позволяет легко учитывать поправки связанные с излучением звука мембраной, совершающей колебания в газовой среде под действием вынуждающей силы, а также решать другие разнообразные задачи, связанные с колебаниями мембран. Учет в методе диссипативных потерь, имеющих место при колебаниях мембраны, позволяет производить расчет колебательных систем с большим затуханием, включая апериодические системы. Преимуществом предлагаемого метода является простота его реализации. Для вычислений и дальнейшего анализа колебательных систем достаточно ввести полученные в результате применения метода формулы в окно компьютерной программы, способной работать с комплексными числами и специальными функциями, и воспользоваться возможностями этой программы (например, построение графиков зависимости от разных входящих в формулы параметров). В противоположность этому, для анализа акустической колебательной системы, в состав которой входит мембрана, пришлось бы решать интегро-дифференциальные уравнения [4], строить решения в виде бесконечных рядов или пользоваться другими вычислительными методами, например, методом конечных элементов. Изложенный в статье метод был развит автором в процессе работы над построением математической модели среднего уха человека (в данном случае барабанная перепонка рассматривается как мембрана).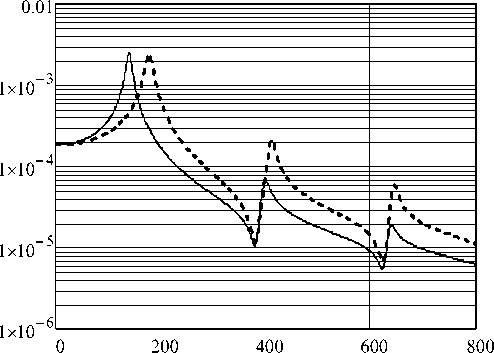
Список литературы Эквивалентные параметры круглой однородной мембраны
- Крендалл И. Б. Акустика. М.: Книжный дом «ЛИБРОКОМ», 2009. 168 с.
- Вахитов Я. Ш. Теоретические основы электроакустики иэлектроакустическая аппаратура. М.: Искусство, 1982. 415 с.
- Канев Н. Г., Миронов М. А. Дипольный резонансный рассеивательзвука//Акуст. журн. 2003. Т. 49, № 3. С. 372-375.
- Смирнов И. П., Бурдуковская В. Г., Кошкин А. Г., Хилько А. И. Нелинейные колебания кольцевых мембраннизкочастотного акустическогоизлучателя//Изв. вузов. Радиофизика. 2008. Т. 51, № 3. С. 199-215.
- Кезик В. И. Вынужденные осесимметричные колебания круглой мембраны, являющейся элементом акустической колебательнойсистемы//Электронный журнал «Техническая акустика», http://ejta.org, 2013, 9.
- Тихонов А. Н., Самарский А. А. Уравнения математическойфизики. М.: Наука, 1972. 735 с.
- Стрелков С. П. Введение втеорию колебаний. М.: Наука, 1964. 440 с.
- Ржевкин С. Н. Курс лекций по теории звука. М.: Изд-во Московскогоуниверситета, 1960. 336 с.


