ЭЛЕКТРИЧЕСКИЕ ПОЛЯ ЦИЛИНДРИЧЕСКИХ РАДИОЧАСТОТНЫХ ТРАНСПОРТИРУЮЩИХ КАНАЛОВ

Устройства изоляции и транспортировки ионов, которые представляют собой последовательность плоских диафрагм той или иной формы с приложенными к ним радиочастотными электрическими напряжениями, достаточно широко распространены [1, 2]. В данной работе будет рассматриваться узкое (в смысле разнообразия конструкций), однако широко используемое подмножество подобных устройств — прямолинейные транспортирующие каналы цилиндрической формы, в большинстве случаев составленные из плоских круговых диафрагм. Более продвинутые аналитические модели электрических потенциалов для радиочастотных транспортирующих каналов сложной формы приводятся в [3–5].

При конструировании аналитических моделей радиочастотных электрических полей используется принцип квазистатичности. При выполнении условия квазистатичности (см. далее) высокочастотный электрический потенциал такого поля можно представить как произведение функции времени, задающей закон изменения напряжений на электродах, и потенциала электростатического поля, соответствующего постоянным напряжениям на электродах.

Предположение о квазистатичности высокочастотного электрического поля справедливо, когда время характерного изменения электрических напряжений на электродах существенно превышает время распространения электромагнитного возмущения в пределах устройства. Типичные размеры электродных конфигураций, используемых в конструкциях ионно-оптических систем, составляют не более нескольких десятков сантиметров (как правило, значительно меньше). С учетом равенства скорости света и скорости распространения электромагнитного возмущения указанное предположение заведомо выполняется для частот электрических напряжений, обычно используемых в ионно-оптических устройствах (от сотен килогерц до нескольких мегагерц, редко — несколько гигагерц).

При таких условиях электромагнитное возмущение распространяется практически мгновенно, в силу чего высокочастотный электрический потенциал, изменяющийся во времени и пространстве, можно представить как произведение функции времени и электростатического потенциала, зависящего от пространственных координат. Зависящий от времени множитель описывает временнóе изменение электрических напряжений, а зависящий от координат потенциал соответствует постоянным напряжениям на электродах, которые изменяются во времени синхронно и пропорционально друг другу.

Иными словами, в рамках квазистатической модели предполагается, что создается такое электрическое поле, которое в каждой точке пространства синхронно и пропорционально изменяется в соответствии с законом изменения электрических напряжений на электродах. Хотя этот шаг представляет собой, по сути, пренебрежение электродинамическими эффектами, т.е. сопутствующей электромагнитной волной, возникающей в соответствии с уравнениями Максвелла при любом изменении электрических и магнитных полей во времени, но он вполне допустим, если частота напряжений, прикладываемых к электродам, не слишком велика (в указанном выше смысле).

РАДИОЧАСТОТНЫЕ КАНАЛЫ ТРАНСПОРТИРОВКИ С КРУГОВЫМИ ДИАФРАГМАМИ

Радиочастотные цилиндрические ловушки и транспортирующие цилиндрические каналы типа SRIG (англ., Stacked Ring Ion Guides) представляют собой последовательность диафрагм одинаковой формы и размера с приложенными к ним синусоидальными радиочастотными либо импульсными электрическими напряжениями [1, 2, 6–10]. Диафрагмы располагаются друг от друга на одинаковом расстоянии и формируют цилиндрический канал транспортировки с прямой осью. На рис. 1 показана типичная цилиндрическая радиочастотная ловушка типа SRIG с круговыми диафрагмами одинакового радиуса.

В типичном случае приложенные синусоидальные радиочастотные напряжения характеризуются сдвигом фазы π между соседними диафрагмами. Это означает, что знаки и амплитуды синусоидальных напряжений, приложенных к отдельным диафрагмам, чередуются по правилу

+ U r , - Ur , + Ur , - Ur , + Ur , - Ur , •••. (1) RRRRRR

Поэтому в любой момент времени напряжения на соседних диафрагмах имеют противоположные знаки, что должно максимизировать напряженность управляющего радиочастотного электрического поля.

В силу симметрии геометрической формы электродов и антисимметрии напряжений, приложенных к электродам, плоскость, вдоль которой электрический потенциал тождественно равен нулю, располагается посередине между соседними электродами. Это позволяет добавить фиктивные диафрагмы с нулевыми напряжениями без искажения электрического поля и тем самым ввести в рассмотрение периодические последовательности диафрагм и напряжений, которые организованы в соответствии с правилом:

+U_R ,0, - U_R ,0, + U_R ,0, - U_R ,0, + U_R ,0, - U_R , .... (2) RRRRRR

Если сдвинуть на один шаг вдоль цилиндрической оси электроды и приложенные к ним электрические напряжения, заданные в соответствии со схемой (2), то получим аналитическое решение для электрического поля, соответствующего напряжениям на диафрагмах, организованным по правилу:

0, + Ur ,0, - Ur ,0, + Ur ,0, - Ur ,0, + Ur ,0, .... (3)

Известно [2], что вдали от краев электродов, в окрестности оси транспортирующего канала, электростатический потенциал такой системы электродов с приложенными к ним периодическими напряжениями, соответствующими последовательности напряжений (1), описывается с хорошей точностью выражением

U (z, r ) =

U R

1 0 ( AR )

cos ( Az + в ) I о ( Ar )

,

Рис. 1. Структура периодических кольцевых электродов цилиндрической радиочастотной ловушки типа SRIG.

где z , r — аксиальная и радиальная координаты ( r = ^ x ² + y ² ); U_R — статические потенциалы, приложенные к диафрагмам; I 0 — модифицированная функция Бесселя нулевого порядка [11–13]; R — радиус круговых диафрагм; β определяет сдвиг последовательности диафрагм относительно начала координат; λ — параметр геометрического масштаба. Для напряжений на диафрагмах по схеме (1) параметр λ равен π / L , где L — расстояние между соседними диафрагмами, для схем (2) и (3) параметр λ равен π / (2 L ). Причина: для схемы (1) расстояние между соседними максимумами и минимумами осевого распределения потенциала, которые соответствуют размещению диафрагм вдоль оси, равно Δ( λz + β ) = λ Δ z = π , где Δ z = L , тогда как для схем (2), (3) расстояние между соседними максимумами/минимумами и нулями осевого распределения равно Δ( λz + β ) = λ Δ z = π / 2.

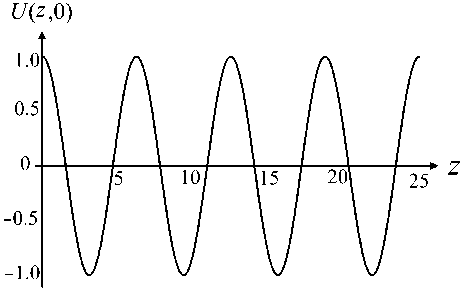
Эквипотенциальные линии и трехмерный график электрического потенциала, заданного формулой (4), в нормированных координатах ( z , r ) показан на рис. 2. Строго говоря, для создания именно такого электрического поля во всем объеме транспортирующей ловушки необходимо, чтобы электроды, формирующие последовательность диафрагм, имели форму эквипотенциальных поверхностей, показанных на рис. 2. Однако на практике достаточно использовать плоские кольцевые диафрагмы с соответствующими электрическими потенциалами. Для таких электродов электрическое поле в середине канала вдали от краев электродов будет с хорошей точностью описываться аналитическим выражением (4) (см. [2]).

b

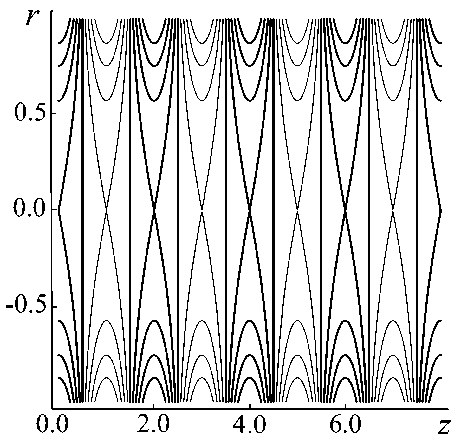
Рис. 2. Статический электрический потенциал (4) в нормированных координатах.

a — эквипотенциальные линии на плоскости ( z , r ), b — поведение потенциала на оси r = 0.

Потенциал (4) представляет собой взвешенную сумму с постоянными коэффициентами, составленную из двух линейно-независимых потенциалов, задаваемых формулами

U C ( z ^, r ) = J UR вЛ cos ( ^A z ) I 0 ( ^r ) ^, I 0 ^{( A R} )

U SS ( z, r ) =

U R

1 0 ( AR )

sin ( Az ) 1 ₀ ( Ar ) .

На оси симметрии r = 0 потенциал (5) ведет себя как U ₀cos ( Az ) , а потенциал (6) — как U ₀sin ( Az ) , где U ₀ = U_R/1 ₀ ( AR ) — амплитуда пространственных колебаний электростатического потенциала на оси системы. Электростатические потенциалы (5), (6) оказываются полезными инструментами для конструирования аналитических моделей электрического поля при сложных конфигурациях радиочастотных напряжений на электродах, включая сюда импульсные напряжения и напряжения со сложным спектром.

Функции (5) могут использоваться для описания электростатического поля периодической последовательности кольцевых диафрагм с напряжениями, соответствующими периодической последовательности напряжений (2), а функции (6) — диафрагм с напряжениями, соответствующими периодической последовательности напряжений

(3). Для этого в формулах (5), (6) необходимо использовать геометрический масштаб A = П ( 2 L ) , где L — расстояние между соседними круговыми диафрагмами.

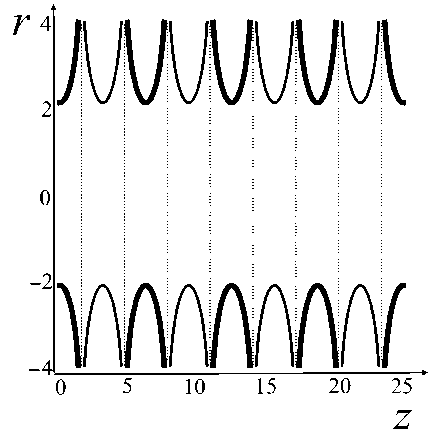
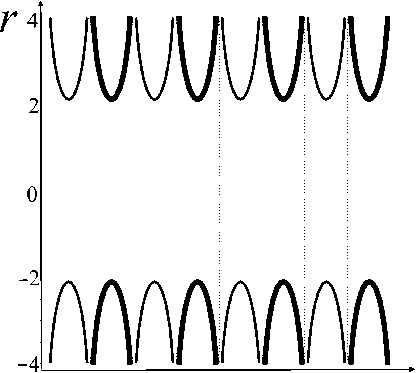
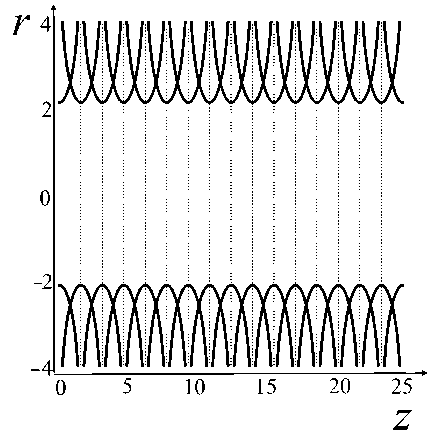
На рис. 3, a, показаны эквипотенциальные поверхности, которые могут использоваться как электроды для создания электрического поля с электрическим потенциалом (5). На рис. 3, b, показаны эквипотенциальные поверхности, которые могут использоваться как электроды для создания электрического поля с электрическим потенциалом (6). Жирными линиями показаны эквипотен-циали U ( z,r ) = + U R , тонкими линиями показаны эквипотенциали U ( z,r ) = – U R , пунктирными линиями показаны эквипотенциали U ( z,r ) = 0.

Электрическое поле устройства может быть суммой электрических полей с потенциалами (5), (6), причем весовые коэффициенты суммы должны контролироваться напряжениями на электродах. Объединить электроды на рис. 3, a, и рис. 3, b, в единую систему невозможно из-за их наложения друг на друга (рис. 3, c). Однако при замене точных диафрагм криволинейной формы на плоские круговые диафрагмы (рис. 3, d) получаем систему электродов, для которой в центральной части транспортирующего канала вдали от краев диафрагм можно с высокой точностью создавать как электрическое поле (5), так и электрическое поле (6), в зависимости от электрических напряжений, прикладываемых к электродам.

a

b

О 5     10     15     20    25

Z

c

d

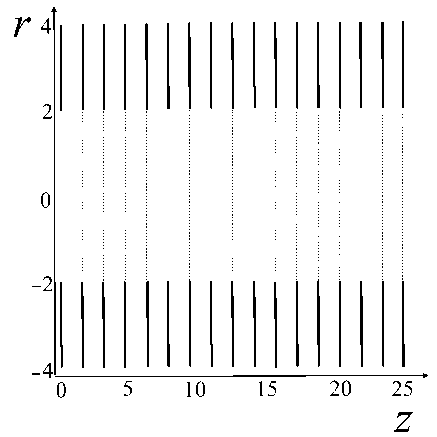
Рис. 3. Осесимметричные эквипотенциальные поверхности, которые могут использоваться в качестве электродов.

а — для электрического потенциала (5), b — для электрического потенциала (6), c — наложение систем электродов "a" и "b" друг на друга, d — огрубленная система электродов "с" в виде плоских круговых диафрагм

Возмущения электрических полей, которые вызываются такой заменой идеальных электродов, рассматриваются далее.

КРАЕВЫЕ ПОЛЯ И ВОЗМУЩЕНИЯ, ВЫЗВАННЫЕ ИСКАЖЕНИЕМ ФОРМЫ ЭЛЕКТРОДОВ

На рис. 3 показан процесс замены идеальных криволинейных электродов на конструктивно бо- лее удобные плоские диафрагмы. Очевидно, при этом происходит искажение точного электрического поля, но из общих соображений можно ожидать, что такие искажения быстро затухают при удалении от краев плоских диафрагм. В данном разделе рассматриваются оценки скорости затухания и определяются критические геометрические параметры плоских диафрагм, при которых искажения электрического поля в центральной части канала транспортировки можно считать незначительными.

Рассмотрим вариант, когда знаки и амплитуды высокочастотных напряжений, приложенных к диафрагмам, чередуются в соответствии с правилом (1). В силу периодичности как геометрии электродов, так и прикладываемых к ним электрических напряжений распределение электрического потенциала вдоль горизонтальной линии r = R представляет собой периодическую функцию и в силу этого может быть разложено в ряд Фурье:

U ( z , R ) = Ur £ U k Sin [ ^П ] .           (7)

k = 1, m       \ L J

Здесь точка z = – L / 2 соответствует диафрагме с напряжением – U R , точка z = + L / 2 соответствует диафрагме с напряжением + U R , точка z = 0 соответствует середине между соседними диафрагмами, L — расстояние между соседними диафрагмами, u_k — нормированные безразмерные амплитуды синусоидальных гармоник ряда Фурье. Как будет показано далее, косинусоидальные гармоники и четные синусоидальные гармоники равны нулю в силу симметрии электродов и электрических напряжений.

Точное решение задачи Дирихле для осесимметричного уравнения Лапласа с краевым условием (7) имеет вид:

^U ( z, r ) = U R £ ^U 2 k - 1

k = 1, »

7 2 k - 1 ) nz \ I о ( ( 2 k - 1 ) nr I )

_v L    J 1 0 ( ( 2 k - 1 ) nR/LУ

где I 0 — модифицированная функция Бесселя нулевого порядка.

Поскольку функция I ₀( ξ ) экспоненциально быстро растет с увеличением аргумента ξ , так что справедлива оценка 1 0 ( ^ ) * e ^/2 -~n при £ - 0.27, то старшие гармоники быстро затухают при смещении по радиусу от границы r = R в сторону оси r = 0. Оценка вклада третьей и пятой гармоник по отношению к первой гармонике при отступе на шаг Δ r от края круговых диафрагм имеет вид

^U 3 ( z , r ) *

^U 1 ( z , ^r )

* _!; 1 о ( 3 n ( R -A r )/ L )     I о ( nR/L )     *

u 1     1 0 ( 3nR/L )     1 0 ( n ( R -A r )/ L )

* exp ( - 3 n A r/L ) ,

^U 5 ( z , r ) *

^U 1 ( z , r )

* ^ I о ( 5 n ( R -A r )/ L )     I о ( nR/L )     *

u ₁     I _о ( 5nR/L )     I _о ( n ( R -A r ) /L )

* exp ( - 5 n A r/L ) .

В частности, уже при R / L ≥ 2 вклад старших гармоник в приосевой области 0 ≤ r ≤ R / 4 пренебрежимо мал.

Экспоненциальный рост электрических потенциалов (4) при удалении от оси r = 0 в сторону границы r = R имеет и другой побочный эффект. А именно, электрическое напряжение U R , прикладываемое к диафрагмам, экспоненциально затухает по мере приближения к оси r = 0:

U о = * UR exp (^{- n R}/L ) , ^(1о) I о ^{( nR}/^L )

где U 0 — амплитуда пространственных колебаний электрического потенциала на оси системы.

В силу формулы (10) при достаточно больших значениях безразмерного параметра R / L управляющее воздействие со стороны высокочастотного электрического поля на ионы, находящиеся вблизи оси, практически отсутствует. В частности, при R ≥ 4 L высокочастотное электрическое поле на оси системы пренебрежимо мало при любых разумных амплитудах синусоидальных напряжений, прикладываемых к электродам транспортирующего канала.

Данный эффект надо учитывать, если требуется управлять движением ионов в приосевой области транспортирующего канала с помощью высокочастотного электрического поля транспортирующего канала. В частности, в случае транспортировки ионов при помощи эффекта А-волны [14– 17] безразмерный параметр R / L должен быть, с одной стороны, достаточно велик, чтобы эффект от воздействия старших пространственных гармоник высокочастотного электрического поля на оси системы был небольшим. С другой стороны, безразмерный параметр R / L должен быть достаточно мал, чтобы на оси присутствовало заметное высокочастотное электрическое поле и чтобы высота псевдопотенциальных барьеров вокруг локальных ловушек А-волны на оси системы обеспечивала захват и принудительную транспортировку ионов.

Для более точной оценки вклада старших пространственных гармоник рассматриваемого электрического поля используем грубую модель для распределения электрического потенциала вдоль горизонтальной линии r = R, при которой в про- межутке между соседними диафрагмами электрический потенциал аппроксимируют прямой линией (рис. 4, a). В силу симметрий краевого условия амплитуды косинусоидальных гармоник и амплитуды четных синусоидальных гармоник обращаются в ноль. Для рассматриваемого краевого условия амплитуды синусоидальных гармоник sin(kπz / L) равны

u k =

L 8

L - H n² k²

sin

kn ^

cos

2 J

knH ^

2 L J

достаточно близким к оптимальному. Кроме того, амплитуда первой гармоники показывает, какая часть приложенных электрических напряжений используется для полезной компоненты радиочастотного электрического поля на оси цилиндрического канала.

Точно также для схемы напряжений (2) и нормированного кусочно-линейного краевого условия на границе r = R , показанного на рис. 4, b, амплитуды синусоидальных гармоник sin( kπz / 2 L ) равны

где L — расстояние между соседними диафрагмами, H — толщина диафрагмы (0 ≤ H ≤ L ), k = 1, 2, 3, … — номер гармоники. В частности, из формулы (11) следует, что все четные синусоидальные гармоники равны нулю, как это и должно быть из-за симметрии формы периодического краевого условия. При H / L = 1 / 3 третья синусоидальная гармоника обращается в ноль, что, по-видимому, является оптимальным выбором для цилиндрических транспортирующих каналов типа SRIG с круговыми диафрагмами или выбором,

u k =

L 16

L - H nk 2

sin

kn ^ 2 J

. (kn > .

sin sin

I 4 J

( ^      ]

I    ^{4 L}    J

. (12)

Стоит обратить внимание, что период краевых условий составляет в этом случае величину 4 L , а не 2 L , что соответствующим образом сказывается как на частотах пространственных гармоник высокочастотного электрического поля, так и на затухании этих гармоник при удалении от края диафрагм.

a

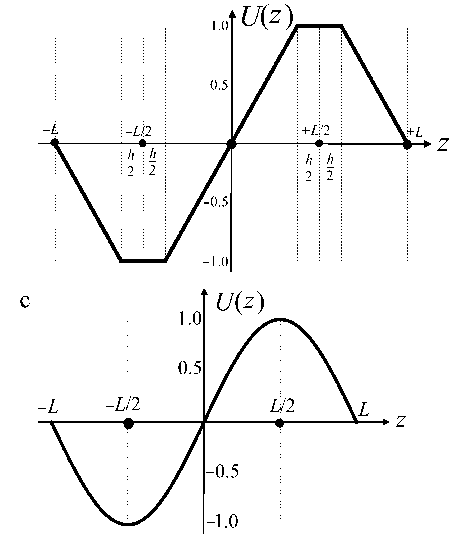
Рис. 4. Нормированное граничное условие вдоль границы r = R.

a — для соседних диафрагм с напряжениями противоположных знаков, b — при наличии промежуточной диафрагмы с нулевым напряжением, c — аналитическое решение (4) без промежуточных диафрагм, d — аналитическое решение (4) с промежуточными диафрагмами

b

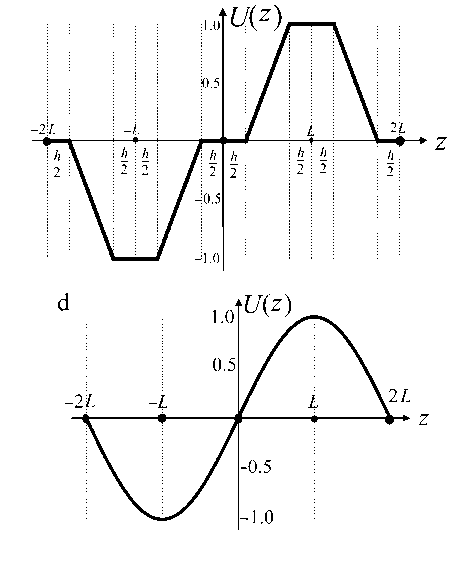
Как и в случае формулы (11), формула (12) наглядно показывает, что четные синусоидальные гармоники разложения краевого условия в ряд Фурье тождественно равны нулю. Для сравнения на рис. 4, c, показано точное краевое условие вдоль границы r = R для аналитического решения (4).

Требуется исследовать, насколько допустимо применять кусочно-линейную аппроксимацию краевого условия при вычислении амплитуд гармоник ряда Фурье. Для этой цели в качестве модельной задачи можно использовать краевое поле плоского конденсатора с тонкими и толстыми электродами, которое рассматривается в [18] (гл. II, §3, п. 39, пример 3).

Известно, что любое решение двумерного уравнения Лапласа (планарный электрический потенциал) можно представить как вещественную часть комплекснозначной аналитической функции комплексного переменного. В частности, если U(x, y) — это потенциал некоторого электростатического поля, удовлетворяющий двумерному уравнению Лапласа, то его всегда можно дополнить такой функцией V(x, y), что u + iv = U(x, y) + iV(x, y) = F(x + iy) (13) будет аналитической функцией комплексного переменного (для этого необходимо и достаточно, чтобы функции U(x, y), V(x, y) удовлетворяли соотношениям Коши–Римана). Если производная функции (13) не равна нулю в какой-то точке, то в окрестности этой точки можно найти обратную аналитическую функцию комплексного переменного x + iy = f(u + iv) = g(u, v) + ih(u, v), (14) так что выполнены тождества x + iy ≡ f(F(x + iy)), u + iv ≡ F(f(u + iv)).

Пара уравнений x = g ( u , v ), y = h ( u , v ) задают двухпараметрическое семейство кривых на плоскости ( x , y ). Однопараметрические линии u = const будут эквипотенциальными линиями электростатического поля с электрическим потенциалом U ( x , y ); однопараметрические линии v = const будут силовыми линиями электростатического поля с электрическим потенциалом U ( x , y ), ортого-нальнми эквипотенциальным линиям.

Для задачи о краевом поле плоского конденсатора с тонкими электродами не удается найти решение в виде суперпозиции элементарных функций, однако обратную функцию (14) можно представить в таком виде ([18], гл. II, §3, п. 39, пример 3):

x (и, v ) = -(| π y ( u,v ) = - (. π

e ^{π v}

e ^{π v}

cos ( пи ) + nv + 1 ) , sin ( пи ) + пи ) ,

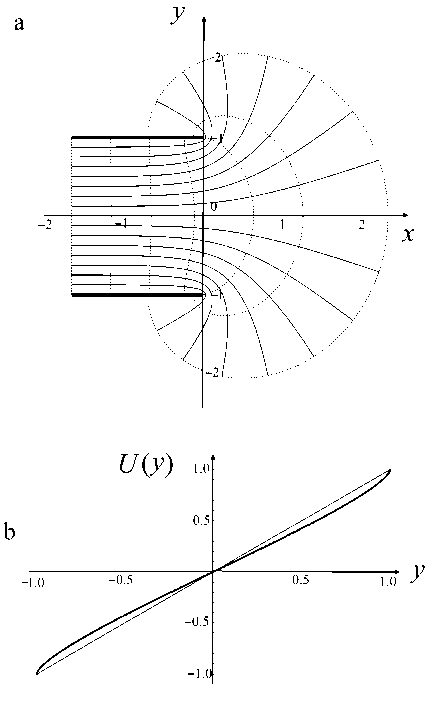
Рис. 5. Решение (15) задачи о краевом поле плоского конденсатора с тонкими электродами.

a — эквипотенциальные линии и силовые линии на плоскости ( x , y ), b — график изменения нормированного электрического потенциала вдоль линии x = 0, y e [-1, +1]

где электрод с напряжением +1 представляет собой тонкую линию y = +1, x ≤ 0, а электрод с напряжением –1 представляет собой тонкую линию y = –1, x ≤ 0. На рис. 5, а, показаны эквипотенциальные линии и силовые линии на плоскости (x, y) для решения (15), на рис. 5, b, — график изменения электрического потенциала вдоль линии x = 0, y e[-1, +1], который получен с помощью численного решения алгебраических уравнений (15). С точностью ±0.004 эта зависимость описывается эмпирической формулой и (У) = У - 41 - У2 (0.223697у + 0.108425у3). (16)

Точно так же для задачи о краевом поле плос-  ние (14) можно представить в таком виде ([18], кого конденсатора с толстыми электродами реше-  гл. II, §3, п. 39, пример 3):

x + i y

v + i u

где электрод с напряжением +1 представляет собой квадрант y ≥ +1, x ≤ 0, а электрод с напряжением –1 представляет собой квадрант y ≤ –1, x ≤ 0. На рис. 6, а, показаны эквипотенциальные линии и силовые линии на плоскости ( x , y ) для решения (15), на рис. 6, b, — график изменения электрического потенциала вдоль линии x = 0, y e [-1, +1], который получен с помощью численного решения алгебраических уравнений (17). С точностью ±0.0025 эта зависимость описывается эмпирической формулой

U ( y ) = y - V 1 - y ² ( 0.171353 y + 0.0389675 y ³) . (18)

Таким образом, для оценки значений гармоник ряда Фурье линейная аппроксимация вполне применима, за исключением случаев моделирования движения ионов в непосредственной близости к краям электродов.

РАДИОЧАСТОТНЫЕ КАНАЛЫ

ТРАНСПОРТИРОВКИ С НЕКРУГОВЫМИ

ДИАФРАГМАМИ

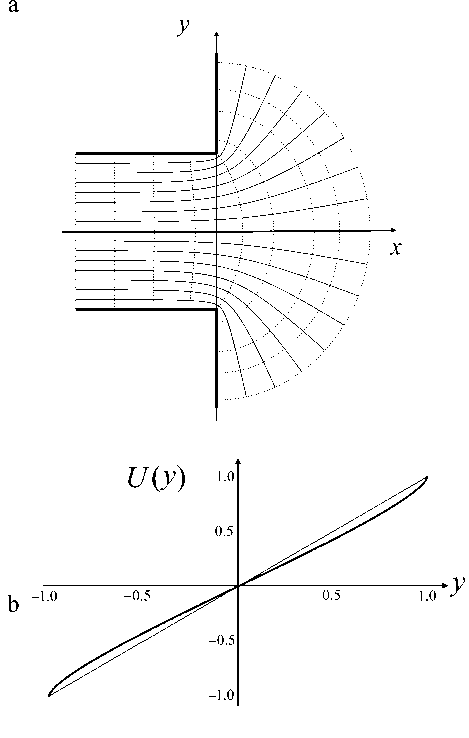
Рис. 6. Решение (15) задачи о краевом поле плоского конденсатора с толстыми электродами.

a — эквипотенциальные линии и силовые линии на плоскости ( x , y ), b — график изменения нормированного электрического потенциала вдоль линии x = 0, y g [-1, +1]

Наряду с аналитическим осесимметричным решением (5), (6) имеются аналитические мульти-польные решения:

^U сс ( z , r ) =

= U ₀cos ( m arctan ( y/x ) ) cos ( /z ) I_m ( /x ² + y ² ) ,

^U sc ( z , r ) =

= U 0 sin ( m arctan ( y/x ) ) cos ( Xz ) I_m ( / x ² + y ² ) ,

^U cs ( z , r ) =

= U ₀cos ( m arctan ( y/x ) ) sin ( Xz ) I_m ( /x ² + y ² ) ,

^U ss ( ^z , r ) =

= U0 sin(marctan(y/x)) sin(Xz)Im (/x2 + y2), где m — натуральное число, а Im — модифицированная функция Бесселя порядка m [11–13]. Первый нижний индекс соответствует выбору косинуса либо синуса для азимутального множителя, второй нижний индекс — для аксиального множителя. В окрестности нуля Im (^)- %mД2mm!), при больших аргументах Im (^) ^ еД-\12п% .

Потенциалам (5), (6) соответствуют диафрагмы с круговыми апертурами (рис. 7), а потенциалам (19) — мультипольные диафрагмы (рис. 8). Суперпозиция этих решений позволяет исследовать каналы с диафрагмами сложной формы. В Приложении на рис. П показаны эллиптические диафрагмы для суммы осесимметричного и квадрупольного потенциалов.

a

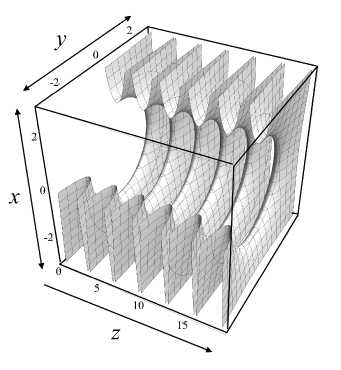
Рис. 7. Точная форма электродов для осесимметричных электрических потенциалов (5), (6). a — трехмерный вид электродов, b — эквипотенциальные линии в сечениях z = const расположения максимумов и минимумов осевого распределения потенциала (форма отверстий)

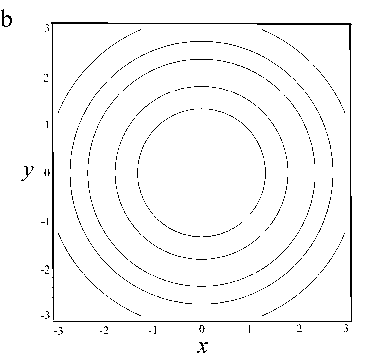
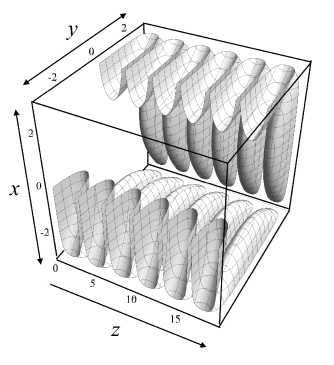
Рис. 8. Точная форма электродов для мультипольного (квадрупольного) аналитического электрического потенциала (первая формула (19) при m = 2).

a — трехмерный вид электродов, соответствующих эквипотенциальным поверхностям, b — эквипотенциальные линии (возможные формы отверстий диафрагм) в сечениях z = const максимумов и минимумов осевого распределения потенциала

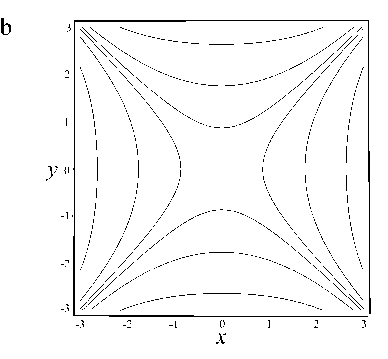
Подобно тому, как для осесимметричных цилиндрических каналов можно использовать плоские диафрагмы вместо диафрагм с криволинейным профилем, для мультипольных каналов можно использовать огрубленное мультипольное сегментирование диафрагм (рис. 9). Как и раньше, для системы электродов с идентичными плоскими муль-типольными либо некруговыми диафрагмами можно прикладывать к четным и нечетным диафрагмам разные электрические напряжения и тем самым создавать электрическое поле, соответствующее взвешенной сумме электрических потенциалов, сдвинутых в пространстве вдоль оси OZ .

Рис. 9. Квадрупольно-сегментированные электроды цилиндрического канала с упрощенным сегментированием электродов.

a

b

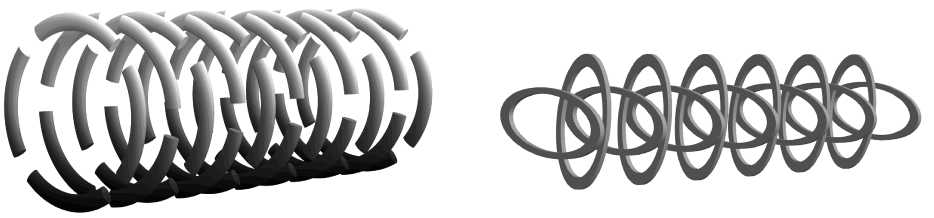
Рис. 10. Цилиндрические каналы с чередующимися диафрагмами.

a — при чередующемся мультипольном сегментировании, b — при чередующихся некруговых диафрагмах разной формы

Более того, можно использовать раздельное мультипольное сегментирование для четных и нечетных диафрагм (рис. 10, a). Результатом будет конфигурация электродов, с помощью которой в канале транспортировки создается электрическое поле, соответствующее взвешенной сумме муль-типольных электрических потенциалов, сдвинутых в пространстве вдоль оси OZ и с разной муль-типольной симметрией. При синтезе каналов транспортировки с некруговыми диафрагмами можно использовать этот же подход для создания каналов, у которых форма четных и нечетных диафрагм отличается (рис. 10, b).

Использование плоских диафрагм вместо диафрагм с идеальным криволинейным профилем (рис. 3), а также мультипольного сегментирования круговых диафрагм вместо идеальных мульти-польных профилей (рис. 11), приводит к появлению паразитных компонентов электрического поля.

Паразитные компоненты электрического поля соответствуют старшим гармоникам при разложении в соответствующие ряды Фурье кусочнолинейных краевых условий для аксиальной координаты (рис. 4) и/или для азимутального угла (рис. 12).

a                                            b

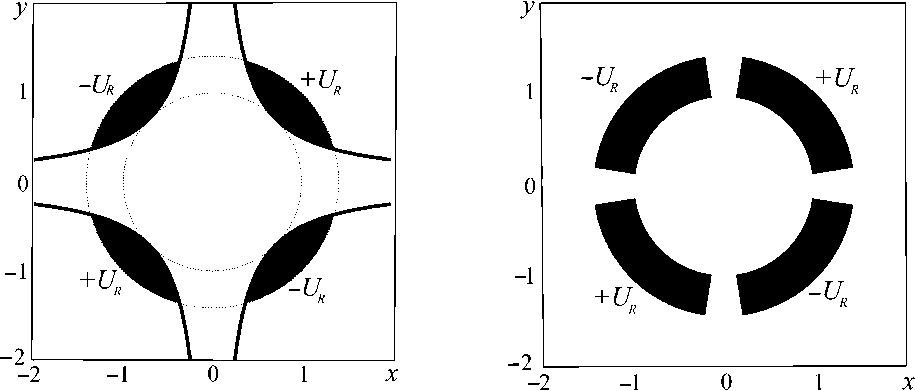
Рис. 11. Форма апертуры мультипольной (квадрупольной) диафрагмы.

а — для точного аналитического решения в сечении z = 0 (первая из формул (19) при m = 2);

b — при мультипольном сегментировании тонкой круговой диафрагмы в сечении z = 0 для m = 2

b

a

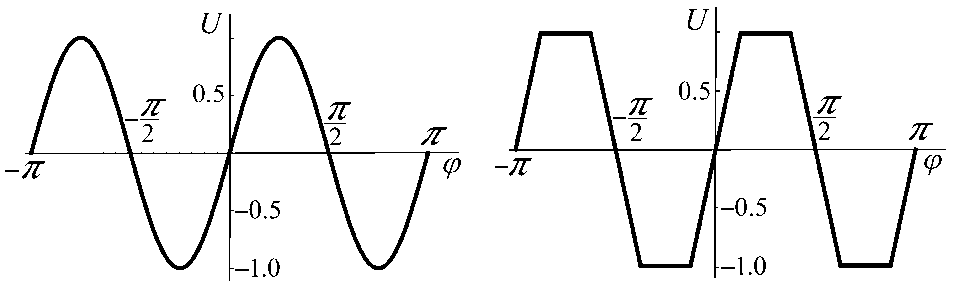
Рис. 12. Краевые азимутальные распределения мультипольного (квадрупольного) потенциала вдоль линий r = const, φ ∈ [0, 2π] в сечениях размещения плоских диафрагм.

а — аналитическое решение, b — сегментированная круговая диафрагма

Аналитические потенциалы (5), (6), (19), (20) позволяют организовывать разложение электрического потенциала, заданного во всем пространстве, в ряды Фурье (возможно, двойные) как по аксиальному, так и по азимутальному направлению. Для этого требуется подставить в эти формулы кратные мультипольные индексы m и/или кратные геометрические масштабы λ . Сопоставление с коэффициентами Фурье огрубленных краевых условий позволяет построить точное аналитическое решение для электрического потенциала возмущенного электрического поля.

С помощью азимутальных рядов Фурье для огрубленного краевого условия, показанного на рис. 12, может быть исследован процесс экспоненциально быстрого затухания паразитных азимутальных старших гармоник, происходящий по мере удаления от краев диафрагм. Это позволяет найти оценки для геометрических характеристик плоских диафрагм, для которых итоговое возмущение электрического поля будет незначительным. Процедура аналогична исследованию затухания старших аксиальных гармоник, которое было выполнено в предыдущем разделе.

ЗАКЛЮЧЕНИЕ

В работе исследовались способы описания электрических полей цилиндрических радиочастотных транспортирующих каналов с помощью аналитических выражений. Показано, что возможно использовать аналитическое представление электрического потенциала не только для главной аксиальной компоненты электрического поля, обычно применяемой при исследовании ионнооптических свойств цилиндрических транспорти- рующих каналов, но и для старших паразитных гармоник. Появление старших паразитных гармоник связано с отклонением реальной формы электродов от идеальной формы, соответствующей эквипотенциальным поверхностям главной аксиальной компоненты электрического поля. Их наличие способно существенным образом исказить функционирование радиочастотного транспортирующего канала. Оценка экспоненциального затухания паразитных аксиальных гармоник по мере удаления от края диафрагм помогает выбирать геометрические характеристики электродов, оптимальные для функционирования устройства.

Показано, как с помощью полученных аналитических выражений можно описывать электрические поля радиочастотных транспортирующих каналов с мультипольными диафрагмами, а также с диафрагмами, обладающими апертурами некруговой формы. Также показано, как можно учитывать влияние паразитных старших азимутальных гармоник электрического поля в случае замены идеальных мультипольных профилей для апертур диафрагм на мультипольно сегментированные круговые диафрагмы. Оценка экспоненциальностепенного затухания паразитных азимутальных гармоник по мере удаления от края диафрагмы помогает выбирать геометрические характеристики электродов, оптимальные для функционирования устройства.

В последующих публикациях планируется исследование особенностей функционирования цилиндрических радиочастотных транспортирующих каналов с помощью псевдопотенциальной модели движения заряженных частиц в высокочастотных электрических полях и аналитических выражений для электрических полей, полученных в данной статье.

ПРИЛОЖЕНИЕ

a

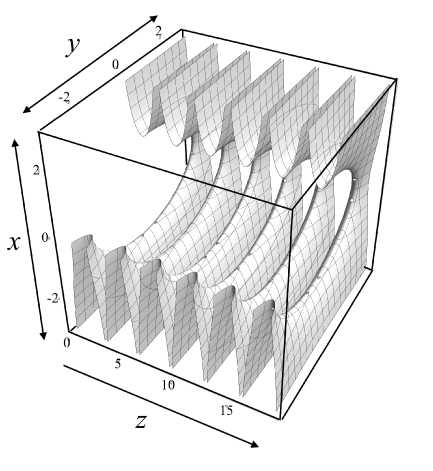
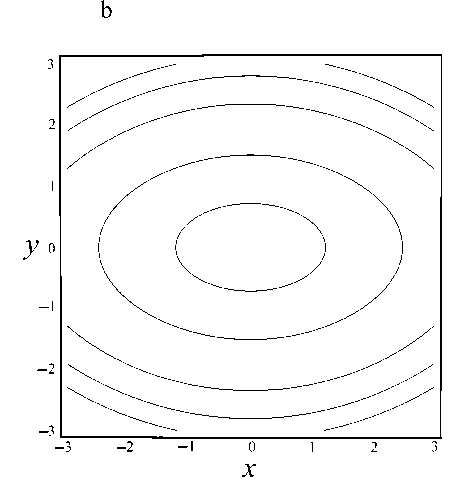
Рис. П. Точная форма электродов для суммы осесимметричных и квадрупольных потенциалов.

a — трехмерный вид электродов, b — эквипотенциальные линии в сечениях z = const расположения максимумов и минимумов осевого распределения потенциала (форма отверстий)

Авторы выражают свою искреннюю благодарность док-ру физ.-мат. наук Михаилу Игоревичу Явору, гл. научн. сотр. Института аналитического приборостроения РАН (г. Санкт-Петербург), за активное и деятельное участие в обсуждении рассматриваемой проблемы и указание на полезные литературные источники, использованные в данном исследовании.

Для аналитических вычислений и создания рисунков использовалась программа Wolfram Mathematica версии 11 Home Edition

.

Финансирование

Исследование выполнено в рамках Государственного задания Министерства науки и высшего образования Российской Федерации № 075-00444-25-00 (от 26.12.2024), тема НИР FFZM-2025-0006 .