Электрические схемы емкостных датчиков микромеханического гироскопа RR-типа

В настоящее время на всех стадиях проектирования сложных устройств и систем используется моделирование. По сравнению с экспериментами на реальной системе или устройстве оно требует меньше затрат, позволяет сделать доступными все выходные переменные и измерять их, не оказывая влияния на них даже в критичных режимах работы. Однако результаты моделирования будут адекватными работе реального объекта, только если оно основано на точных моделях, обеспечивающих приемлемое представление о нем.

Это в полной мере относится и к микромехани-ческим гироскопам, которые являются сложным мехатронным устройствам [1–3]. Для моделирования мехатронных устройств используется широкий диапазон программ: математических общего назначения (Matlab, Mathematica), исходно созданных для проектирования электроники (SPICE, VHDL, SABER, VHDL-ARMS, APLAC, SPECTRE), специализированных коммерческих (MEMS PRO, COVENTOR) и открытых университетских (NODAS, SUGAR). Однако перед использованием программ моделирования, которые зачастую недоступны отечественному разработчику, целесообразно оценить неидеальности используемых в этих программах моделей, произвести оценку возможных результатов, что называется, вручную с помощью общедоступных средств.

Целью данной работы является создание простых моделей для емкостных датчиков микромеханиче-ского гироскопа в виде электрической схемы.

ИДЕАЛИЗИРОВАННАЯ ЭЛЕКТРИЧЕСКАЯ СХЕМА МИКРОМЕХАНИЧЕСКОГО УЗЛА

ГИРОСКОПА

Микромеханический гироскоп (ММГ) вибрационного типа включает в себя микромеханиче- ский резонансный подвес подвижной массы (ПМ), емкостные датчики момента и перемещения ПМ и электронные узлы [4]. Емкостные датчики выполняют ключевую роль в ММГ, являясь по сути интерфейсом между микромеханической и электронной частями.

Для адекватного моделирования работы ММГ необходимо иметь достоверные и верифицированные модели емкостных датчиков. На начальном концептуальном уровне емкостные датчики могут быть представлены в виде конденсаторов с изменяемой в зависимости от положения ПМ емкостью. Для ММГ, в которых ПМ совершает поступательные движения (такие ММГ относят к классу ММГ LL-типа), эта зависимость может быть рассчитана (конечно, без учета краевых эффектов) по известной формуле для плоского конденсатора:

C= εε0S , (1) d где ε0, ε — соответственно диэлектрическая постоянная вакуума и относительная диэлектрическая постоянная среды между электродами, S — площадь перекрытия и d — зазор между электродами.

Существуют также ММГ RR-типа [4, 5]. В них ПМ колеблется вокруг осей подвеса. Основные элементы микромеханической части ММГ RR-типа показаны на рис. 1. Резонансный подвес ПМ над основанием 1 в этом ММГ выполнен с помощью опоры 2 и торсионов 3. ПМ распределена в основном в секторах 4. На боковых поверхностях этих секторов имеются зубцы 5, 6. На основании 1 сформированы статоры 7, 8 с зубцами, которые выполнены так, что между ними находятся зубцы 5, 6 ротора. Под секторами 4 ПМ на основании сформированы электроды 9, 10. ПМ может совершать колебания вокруг осей Z и X.

Зубцы ПМ и статоров 7, 8 образуют так называемую гребенчатую электродную структуру, на основе которой формируют емкостные датчики

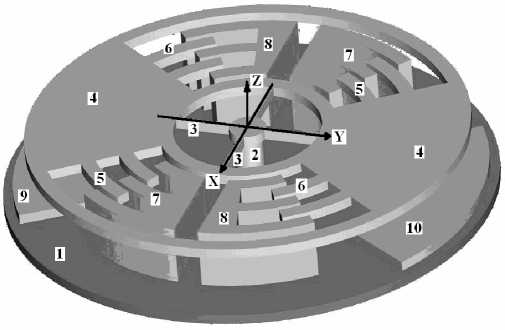
Рис. 1. Принципиальная схема ММГ RR-типа.

1 — основание; 2 — опора; 3 — торсионы; 4 — сектора ПМ; 5, 6 — зубцы ротора; 7, 8 — зубцы статора; 9, 10 — электроды

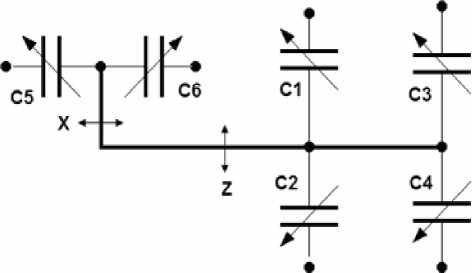
Рис. 2. Электрическая схема электродных структур ММГ

момента и перемещения ПМ вокруг оси Z. С помощью емкостных датчиков, образованных секторами 4 и электродами 9, 10 в ММГ измеряют перемещения ПМ вокруг оси X. В конструкции ММГ на рис. 1 шесть емкостных датчиков образованы 12 парами электродов.

Эти шесть емкостных датчиков могут быть представлены в виде электрической схемы с шестью конденсаторами переменной емкости, которая показана на рис. 2. Утолщенной линией на этой схеме выделена проводящая ПМ, которая является общим электродом всех конденсаторов.

Пары конденсаторов С1, С2 и С3, С4 образованы ПМ и рядом расположенными статорами 7, 8. Емкости каждой пары конденсаторов изменяются в противоположных направлениях при поворотах ПМ вокруг оси Z. В противоположных направлениях изменяются и емкости конденсаторов С5, С6 при поворотах ПМ вокруг оси X.

Схема на рис. 2 позволяет определить напряжение между электродами ММГ при известных входных напряжениях и емкостях конденсаторов. Электрические схемы могут рассматриваться как одна из первых видов моделей, которые и в настоящее время используются при моделировании и в современных программах, таких как PSPICE, Saber, Dymola.

Зависимости емкостей С1–С4 от угла поворота ПМ вокруг оси Z (обозначим его γ ) достаточно просто могут быть выведены из выражения (1) или найдены в литературе, в том числе и учебной [4, 6, 7]:

C i = C 0i (1 ± Y- ), γ ₀

где С 0 i — емкость i -го датчика ( i = 1, ..., 4) при угле γ = 0 (соответствует начальному углу перекрытия между зубцами электродов γ 0 ).

Выражения для расчета зависимости емкости конденсатора, образованного электродами в форме секторов круга, от угла между ними, который обозначим α (так же, как и угол поворота вокруг оси X), в литературе не было найдено. Единственная формула для электродов такой формы была обнаружена в работе [8]. Она имеет вид d С d a

» 2Ц- sin(2 ^ )( R 1 - R 0 ),

т. е. позволяет определять крутизну

^ d C j ( a ) )

—----I ем- ( d ^a )

костного датчика в одной точке при α = 0. Однако одной этой величины (крутизны) недостаточно для моделирования работы емкостных датчиков в ММГ. Она не позволяет оценить создаваемый такой парой электродов момент М при разных углах α и вносимую отрицательную жесткость k е [9] или электрическую податливость [10].

Отметим, что последние могут быть найдены из выражений

U2 dC(α) 2dα k _ U2 d2 C(a) e = 2 d a2 ,

если известны разность напряжений между электродами и зависимость С ( α ). Эта зависимость С ( α ) была определена двумя способами.

В первом способе межэлектродная емкость была представлена как сумма емкостей конденсаторов, образованных элементарными площадками, выделенными на одном электроде, и их проекциями на другой электрод. Такой подход использован, например, при создании для программы APLAC

б

a = 0.214, b = 1.58, c = –1.72

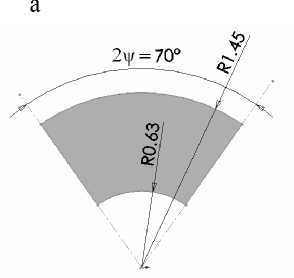
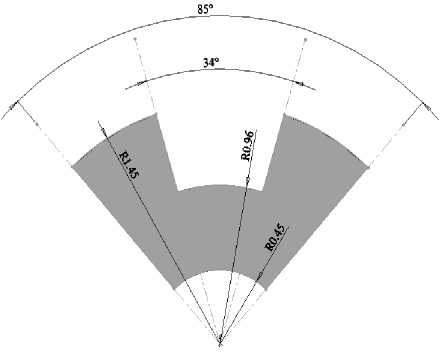
Рис. 3. Форма электродов, располагаемых на крышке ММГ. В рамках указаны значения коэффициентов аппроксимации (7)

в

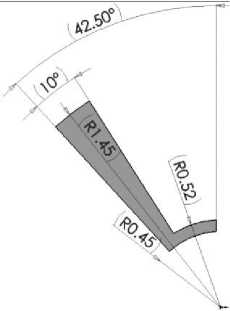
a = 1.23, b = 8.14, c = –9.92

a = 0.218, b = 1.93, c = –1.93

модели емкостного датчика с электродами, имеющими форму прямоугольных пластин [3]. Для емкости между ПМ и электродом 10 при таком подходе может быть получено следующее выражение:

T R max______rdrd 9______ о Jrmin d + rsin(a)cos(9),

где r — расстояние от центра окружностей, ограничивающих электрод; θ — угол между радиусом, проходящим через середину электрода, и радиусом, проходящим через середину элементарной площадки; 2 ψ — угол между крайними радиусами электрода.

Интегрирование правой части выражения с использованием программы символьных вычислений, например Mathematica, возможно, однако получаемое при этом выражение громоздко и не годится для инженерного анализа. Поэтому выражение (6) целесообразно использовать для получения численных значений емкости С при разных значениях угла и последующей аппроксимации полученных значений.

Второй способ определения этой зависимости заключается в получении численных значений емкости С при разных значениях угла с помощью программы расчета емкостей методом конечных элементов. Например, в программе Ansys это может быть выполнено с использованием специального макроса Сmatrix [11]. Для полученных значений емкости, как и в предыдущем способе, определяется аппроксимирующая функция.

На практике могут встречаться электроды более сложной формы, чем электроды 9, 10, например такие, которые приведены на рис. 3, б и 3, в. Однако последние могут быть получены путем

композиции электродов простой формы (как на рис. 3, а). Расчет с использованием программы An-sys может вестись для электродов произвольной формы, при этом в расчете учитываются и краевые эффекты, что позволяет получить более точные результаты, особенно для относительно больших углов и малых расстояниях между электродами.

Расчеты описанными двумя способами были выполнены для электродов, приведенных на рис. 3. В качестве аппроксимирующей функции была выбрана функция вида

У = ,        „ 2

a + b a + c a

или, обозначая величину y при α = 0 как С (0) ( a = ( С (0)^–1)), эту функцию можно представить в виде

C ( a ) =

C (0)

1 + d i a + d 2 a

где d 1 = b / a , d 2 = c / a .

Один коэффициент функции (7) может быть определен точно — коэффициент a . Величина С (0) может быть рассчитана по известной формуле для конденсатора с параллельными электродами. Поэтому необходимо подобрать только два коэффициента для аппроксимации полученных расчетных данных. Расчеты показали, что за счет подбора только двух коэффициентов ( d 1 и d 2 ) для функции (8), можно достичь погрешности аппроксимации менее 1 % от диапазона изменения емкости.

Описанным способом были определены коэффициенты функции (4) для электродов разной

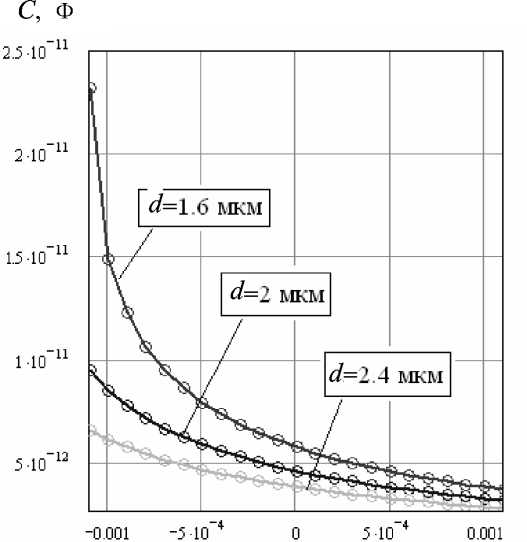
α , рад

Рис. 4. Зависимость емкости С от угла а поворота ротора для разных значений зазора d формы, которые приведены на рис. 3, при величине зазора между ними, равной 2 мкм. (Для удобства применения коэффициенты определены так, что при подстановке в формулу (3) значений углов α в градусах величина емкости определяется в пикофарадах).

Семейство кривых С ( α ) с нанесенными на них полученными расчетным путем значениями (показаны кружочками) приведено на рис. 4. Эти зависимости построены для электродов, показанных на рис. 3, а. Целесообразно отметить, что расчеты достаточно проводить только для одного из электродов с одинаковыми размерами. Зависимость емкости для другого электрода будет отличаться только знаком коэффициента b .

Таким образом, для эквивалентной электрической схемы на рис. 2 могут быть определены необходимые параметры и зависимости. Эта схема может использоваться как для определения межэлектродных напряжений, так и для определения влияния этих напряжений на микромеханическую часть.

ЭЛЕКТРИЧЕСКАЯ СХЕМА МИКРОМЕХАНИЧЕСКОГО УЗЛА ГИРОСКОПА, ВЫПОЛНЯЕМОГО ПО ТЕХНОЛОГИИ "КРЕМНИЙ НА ИЗОЛЯТОРЕ" (КНИ)

Конструкция реального ММГ может отличаться от конструкции, приведенной на рис. 1, иметь

а

Рис. 5. SEM-фотография ротора ММГ (а) и схема расположения электродов на крышке (б)

б особенности, обусловленные технологией изготовления. Так, например, разрабатываемый в ЦНИИ "Электроприбор" ММГ RR-типа выполняется с использованием двух пластин кремния по технологии КНИ [12]. На одной пластине кремния (основании) выполняются опора с торсионами, статор и ПМ, а на другой пластине (крышке) выполняются электроды. На рис. 5, а приведено изображение основания с элементами, а на рис. 5, б показана упрощенная конфигурация электродов, которая совпадает с приведенной на рис. 1. Между опорой, статорами и основанием имеется слой изолятора (диоксида кремния) толщиной 2 мкм, а между электродами и крышкой толщина изоляционного слоя менее 1 мкм. Крышка и основание свариваются между собой по периметру, на котором также имеется слой изолятора.

Для такой конструкции схема на рис. 2 должна быть дополнена парой конденсаторов С7, С8, как это показано пунктирными линиями на рис. 6. Конденсатор С7 в этом случае образован тем сектором 4 ПМ, одна сторона которого находится напротив электрода 9. Емкость конденсатора С7 изменяется в противоположном направлении при поворотах ПМ вокруг оси. Аналогично по отношению к емкости конденсатора С6 ведет себя и емкость конденсатора С8.

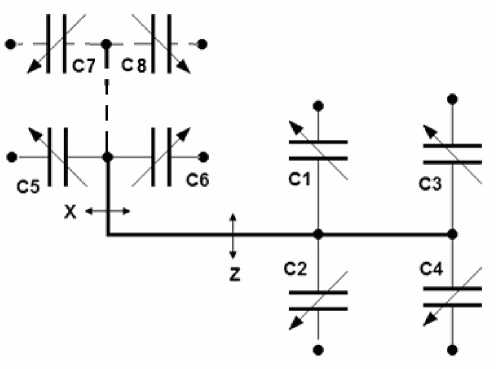
Рис. 6. Дополненная электрическая схема электродных структур ММГ

К этому изменению схемы необходимо добавить еще дополнительные элементы: паразитные емкости между элементами конструкции и проводящим кремнием основания и крышки, а также связи между паразитными емкостями через проводящий кремний. Полученная таким образом электрическая схема приведена на рис. 7.

Паразитные емкости С П , рассчитанные по формуле для конденсатора с плоскопараллельными электродами и определенные экспериментально, представлены в таблице.

Все сопротивления на этой схеме менее 100 Ом, за исключением сопротивления R Т (омического сопротивления торсионов). Оно для одной из модификаций торсионов может быть оценено величиной 150–1500 Ом (зависит от свойств кремния и геометрических размеров торсионов).

В зависимости от цели и типа анализа при моделировании могут использоваться разные схемы.

ОЦЕНКА РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ ЕМКОСТНЫХ ДАТЧИКОВ ММГ RR-ТИПА

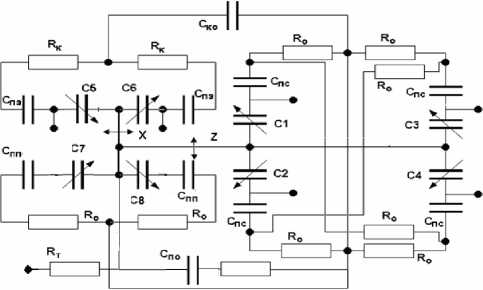
Рис. 7. Электрическая схема ММГ, дополненная паразитными связями

Схема с паразитными емкостями (рис. 7) может использоваться для оценки их влияния на работу контуров управления, определения разрешающей способности используемых емкостных датчиков и т. д. Примеры подобного анализа содержатся в работах [13–15].

Проведем оценку разрешающей способности емкостного датчика на оси вторичных колебаний ПМ (на емкостях С5, С6) для случая, когда высокочастотное напряжение подается на ПМ и измеряется разность токов, протекающих через емкости С5, С6 в схеме с трансрезистивным усилителем [16, 17]. На рис. 8 приведена схема преобразования емкости С5 в напряжение U вых . Здесь показано, что один вывод емкости С ПЭ соединен с общим, т. к. на практике, как правило, вывод от основания и/или крышки соединяют с общим. Это сделано для

Емкости конденсаторов электрической схемы на рис. 7

Емкость конденсатора	Обозначение	Величина (пФ)
Электрод—ПМ (крышка)	C5 , C6	4.5
Электрод—кремний (крышка)	С ПЭ	70
Проекция сектора 4 на основание—ПМ	C7 , C8	4.5
Проекция сектора 4 на основание—крем-ний (основание)	С ПП	20
Статор—ПМ	С1–С4	2
Опора—основание	С ПО	1
Емкость между крышкой и основанием	С КО	80

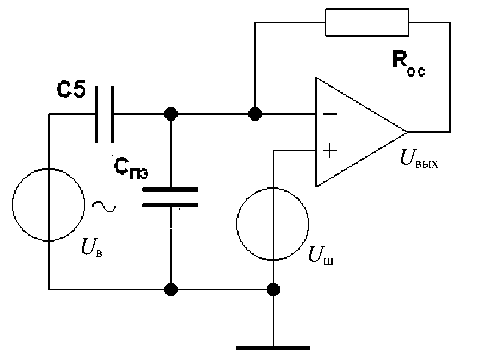
Рис. 8. Схема преобразования емкости в напряжение

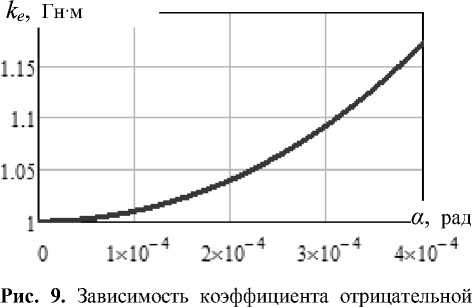
жесткости от амплитуды вторичных колебаний ПМ

уменьшения внешних помех, т. к. в этом случае проводящие основание и крышка выполняют функцию электростатического экрана. Анализ работы этой схемы (на основе формульных соотношений или с использованием программ моделирования типа PSPICE) позволяет сделать вывод, что:

– наличие паразитной емкости С ПЭ ухудшает устойчивость схемы и может привести к резонансному усилению шумов;

– при С ПЭ >> С5 (как это имеет место в рассматриваемом ММГ) для разрешающей способности Δ С схемы на рис. 8 может быть получена следующая оценка:

A C « С ПЭ

U ш U в

где U Ш , U В — напряжения шума и возбуждения.

На основании этой оценки был сделан вывод о целесообразности увеличения толщины изоляционного слоя между электродами канала вторичных колебаний и кремнием основания в случае технологии КНИ. Отметим также, что схема на рис. 7 может быть использована для оптимизации площади электродов.

ВЛИЯНИЕ НАПРЯЖЕНИЯ ВОЗБУЖДЕНИЯ ЕМКОСТНЫХ ДАТЧИКОВ НА РЕЗОНАНСНУЮ ЧАСТОТУ ПОДВЕСА ПМ

Проведем анализ влияния амплитуды вторичных колебаний на изменение резонансной частоты подвеса ротора по оси вторичных колебаний. Для этого обратимся к схеме на рис. 2. Полагая, что для измерения перемещений ПМ в ММГ используется схема с подачей переменного высокочастотного напряжения на ПМ (как это показано на рис. 8), получим, что напряжения на конденсаторах С5, С6 равно U в (на практике действующее значение U в = 1–2.5 В).

Полагая, что амплитуда колебаний ПМ вокруг оси равна A , определим среднюю за период колебаний ПМ величину k e для одной пары электродов, которая на схеме обозначена С5 (или С6) по формуле (5):

__ U 2_J ₈ ² C i (x(t» _d ei 2 n J ^J0    d x ( t )²

где x = A sin

f 2 n ) .     _ _                 _

t ; i — номер конденсатора на

I ^Ji )

рис. 6; Т 1 — период первичных колебаний ПМ.

Результаты расчета при Uв= 1 В для электрода, имеющего приведенные на рис. 3, а размеры, показаны на рис. 9. Видно, что величина ke при изменении амплитуды вторичных колебаний ПМ от 0 до 0.0004 радиана изменяется примерно на 20 %. При напряжении между ПМ и электродами 1– 2.5 В такое изменение ke может приводить к изменению резонансной частоты fp подвеса ротора на 1 %, что при fp = 3 кГц составляет 30 Гц. Такое изменение может существенно сказаться на нелинейности характеристики ММГ при работе со сведенными резонансными частотами подвеса ПМ, снизить эффективность работы со сведенными резонансными частотами при измерении больших угловых скоростей.

Переходя к эквивалентной электрической схеме на рис. 6 с 4 конденсаторами по оси вторичных колебаний и учитывая то, что величины k e , рассчитанные для каждого конденсатора, необходимо суммировать, можно сделать вывод о целесообразности уменьшения емкостей С7, С8, которое может быть достигнуто увеличением зазора между ПМ и основанием.

ВЫВОДЫ

• 1.    Разработаны эквивалентные электрические схемы емкостных датчиков ММГ RR-типа, изготавливаемых по технологии КНИ, и проведена их экспериментальная проверка.

• 2.    Проведен анализ работы ММГ на основе эквивалентных электрических схем и получены рекомендации по повышению точности ММГ, улучшению его конструкции и оценка возможности работы при сведенных резонансных частотах подвеса подвижной массы.

Эквивалентные электрические схемы емкостных датчиков ММГ могут использоваться при анализе совместной работы микромеханического и электронного узлов, а также при анализе работы каждого из этих узлов.

Работа выполнена при поддержке гранта РФФИ 07-08-006969.