Электродинамический анализ электромагнитных полей круглого волновода с тонкими металлическими ребрами

С развитием СВЧ-техники к создаваемым и применяемым волноводным устройствам предъявляются более высокие уровни требований, а именно: большая передаваемая мощность, более высокие добротности, меньшие потери и более широкий диапазон одномодового режима. Это приводит к тому, что элементная база СВЧ-устройств постоянно усложняется, требуя разработки новых узлов, а также методов и алгоритмов их анализа и синтеза.

Известно, что применение современных программных пакетов компьютерного моделирования элементов и устройств СВЧ-диапазона хотя и позволяет рассчитывать характеристики практически любого сложного узла с применением универсальных сеточных методов, обладает существенными ограничениями в области синтеза, поскольку с одной стороной требует значительного времени для расчетов, а с другой без хорошего начального приближения достаточно часто вообще не приводит к желаемому результату. Таким образом, разработка высокоскоростных алгоритмов и программ электродинамического анализа и синтеза по-прежнему является актуальной задачей.

Вышесказанное в полной мере относится и к цилиндрическим волноводным структурам с тонкими металлическими ребрами. Такие волноводы находят широкое применение в современ- ных устройствах СВЧ [1–6]. Они используются в приемных и передающих антеннах, в устройствах, предназначенных для получения круговой поляризации, в делителях мощности. Кроме этого, такие волноводные структуры обладают частотно-селективными свойствами, поэтому успешно применяются для построения фильтров.

Количество работ, посвященных электродинамическому анализу круглых волноводов с радиальными металлическими ребрами, невелико [1–6]. При этом большинство авторов приводят расчеты только критических волновых чисел и постоянных распространения для достаточно ограниченного числа волн и геометрических размеров волноводов. Необходимо отметить, что несмотря на наличие явных математических выражений для расчета компонент электромагнитных полей, практически отсутствует расчет и визуализация полей Н- и Е-волн. А именно это открывает возможности для дальнейшей разработки алгоритмов по анализу и синтезу различных устройств на базе данного волновода, включая и частотно-селективные устройства.

Таким образом, в данной работе приведено решение задачи электродинамического анализа критических волновых чисел и компонент электромагнитных полей круглого волновода с тонкими радиальными металлическими ребрами. Для повышения точности и скорости вычислений в разработанных алгоритмах реализован учет особенности поведения поля вблизи тонкого металлического ребра.

1. Постановка задачи

Рассмотрим круглый волновод с бесконечно тонкими металлическими ребрами, структура которого показана на рис. 1.

Для решения поставленной задачи будем использовать метод частичных областей (МЧО) с учетом особенности поведения электромагнитного поля на ребре. Тогда согласно данному методу разобьем сечение волновода на две области, используя следующие условия: r е [ 0; r ] — первая частичная область; r е [ r 1 ; r ] — вторая частичная область.

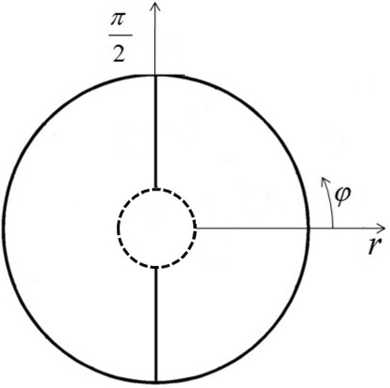
Рис. 1. Структура круглого волновода с тонкими металлическими ребрами

Кроме этого необходимо задать граничные условия, которые определим следующим образом: пусть g = 0 для электрической стенки, g = 1 для магнитной стенки, тогда в случае электрической стенки граничные условия имеют вид:

F 2 m ^{( r} ) = J 2m + g ^{( kr} ) ⁺ P m N 2 m + g ^{( kr} ) •           ⁽⁷⁾

Тогда, используя введенные обозначения, уравнения примут следующий вид:

да

HZ = £ Am cos m=0

(2 m + 1 - g ) Ф- П g

F 1 m ( r );

E z = 0,

H = 0, d n

H z ²

да

£ Bm cos m=0

⁽ 2 m + g ) ф^-П g F 2m ⁽ r )•

а в случае магнитной стенки:

-z = 0, H z = 0.                           (2)

d n

На границе раздела двух частичных областей введем неизвестную функцию f ( ф ) , которую определим следующим образом:

2. Запись компонент поля в частичных областях в случае Н-волн

E Ф = C П f ( ф ) ^пр^{и z} = ^r 1 ,                      ⁽¹⁰⁾

В случае Н-волн z - компоненты поля в двух частичных областях с учетом граничных условий будут иметь следующий вид:

да

H Z = £ A m cos m = 0

где C = ^0.

k

Неизвестные коэффициенты A_m и B_m в разложениях можно определить через функции f ( Ф ) , которые заданы на разделе частичных областей, из следующих уравнений:

^x J 2 m + 1 - g ^{( kr} ) ^;

да

H z ² = £ B_m cos m = 0

( 2 m + 1 ^- g ) ф^-П g

( 2 m + g ) ф- П g

^x [ J 2 m + g ^{( kr} ) ⁺ P m N 2m + g ^{( kr} ) ] ,

x

где J 2 m + 1 - g ( kr ) , J 2 m + g ( kr ) — функции Бесселя первого рода; N_{m +} g ( kr ) — функция Бесселя второго рода; A_m , B_m – неизвестные числовые

коэффициенты; а P_m определим как:

Р™ = m

J 2 m + g ^{( kr} 2 ) N m + g ( kr 2 ) ’

где штрих обозначает производную по аргументу.

Для удобства описания введем следующие обозначения:

F 1 m ^{( r} ) = J 2 m + 1 - g ( ^kr ) ^;

Am = , ¹ . x m   F{m ( r 1 )

п /2

x J f ( ф ) cos ( 2

!m + 1 - g ) ф-П g d ф =

F 1 m ( r 1 )

Bm = п/2

^{(- 1 )} i ^4" J 2 i + g

----------x

Ц m F 2m ^{( r} 1 )

x f f ( ф ) cos ( 2 m + g ) ф-^П g d Ф =

= —1__ L_ ( - 1 ) i П 2

Ц m F 2m ( r 1 ) F 1 m ( r 1 )       4

^x J 2i + g f П ( 2 m + g ) ) •

А неизвестные функции f ( ф ) , использованные в формуле (10), будут иметь следующий вид [7]:

\2  1/2 v

I 2ф|I

f ^(ф) = ¹ I I         / C i T i + g I I ,

V п 7     “ V п 7

L            J где T2i – полином Чебышева.

Таким образом, определив функции f ( ф ) , мы получаем систему алгебраических уравнений относительно неизвестных коэффициентов C_i :

N

Z D ( k , у ) = 0;                       (14)

i = 0

N

^ CiDhj ( k ) = 0.

i = 0

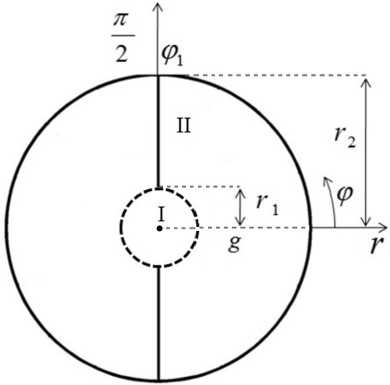
Рис. 2. Разбиение поперечного сечения волновода на области тельно значения констант, получим семейство силовых линий, относительная плотность которых пропорциональна напряженности поля.

Приравнивая определитель данной системы к нулю, получаем уравнение для определения критических волновых чисел:

det D* (k) = 0 , где Dj (k) имеет следующий вид:

”

Dj (k )=Z r ;7’ J2 i+g |П(2 m + 1 — 9 )|X m=0 9m(r1)      V 2            7

X J2j+9 VП(2m + 1 — 9 )]-

TO

-z

m = 0

^F2 m ( r ) H m^F2 m ^{( r} 1 )

J2i+g VП(2m + g)p

3. Расчет и моделирование электромагнитных полей

Неизвестные коэффициенты разложения С_i можно найти из решения системы линейных, но уже неоднородных уравнений, которая получается из (15) путем отбрасывания первого уравнения и переноса первого столбца СЛАУ в правую часть. При этом полученные решения будут верны с точностью до постоянного множителя, определяемого из условия нормировки мощности падающей волны через поперечное сечение волновода.

Для моделирования силовых линий электромагнитного поля Н-волн в волноводе с воздушным заполнением на критической частоте достаточно ограничиться построением силовых линий электрического поля [8; 9]. При этом задача построения силовых линий сводится к нахождению изолиний z -ой компоненты поля этих волн:

H z ( x , y ) = const.

Каждому значению константы соответствует своя силовая линия. Задавая в (18) последова-

4. Результаты расчетов

Представим основные результаты электродинамического анализа круглого волновода с бесконечно тонкими радиальными металлическими ребрами. В табл. 1 приведено исследование сходимости МЧО с учетом особенности электромагнитного поля на ребре для критических волновых чисел первых четырех Н-волн для граничного условия типа электрической стенки ( g = 0), по параметрам ограничения метода M и N при Г 1 / Г 2 = 0.35, ф 1 = п /2. Из таблицы видно, что с увеличением числа учитываемых элементов в рядах – M, критические волновые числа монотонно убывают, а при увеличении порядка приближения метода – N, наоборот возрастают. Сравнение полученных результатов с прямыми численными методами также показывает хорошее совпадение. Аналогично, в табл. 2 представлены результаты исследования сходимости метода для первых четырех Н-волн для граничного условия типа магнитной стенки ( g = 1).

На рис. 3. приведены зависимости критических волновых чисел первых четырех мод круглого волновода с тонкими металлическими ребрами от соотношения r ₁/ r ₂, т. е. от высоты ребра. Причем в спектре волновода первая и третья моды будут иметь граничное условие g = 0, а вторая и четвертая — g = 1. При Г 1 = ? 2 исследуемая структура сводится к простому круглому волноводу, а при увеличении ребра наблюдается уменьшение значения критических волновых чисел всех представленных мод, при этом полоса одномодового режима волновода сужается. Снижение значения критического волнового числа основной моды волновода по сравнению с простым круглым волноводом возможно более

Таблица 1

Сходимость МЧО с учетом особенности на ребре для первых четырех Н-волн круглого волновода с тонкими металлическими гребнями в соотношении r ₁/ r ₂ = 0.35, g = 0

N	M					CST Microwave Studio
	10	30	50	80	100
	1.3327	1.3284	1.3279	1.3276	1.3259
1	3.0706	3.0664	3.0659	3.0656	3.0639
	5.2245	5.2217	5.2213	5.2211	5.2200
	7.0270	7.0036	7.0009	6.9993	6.9896
	1.3336	1.3287	1.3281	1.3278	1.3259
2	3.0908	3.0897	3.0895	3.0894	3.0891
	5.2247	5.2217	5.2213	5.2212	5.2200
	5.3182	5.3168	5.3166	5.3165	5.3160
	1.3348	1.3289	1.3283	1.3279	1.3259	1.3211
3	3.0921	3.0904	3.0902	3.0901	3.0895	3.0814
	5.2270	5.2226	5.2222	5.2219	5.2204	5.2019
	5.3222	5.3218	5.3218	5.3218	5.3217	5.3087
	1.3367	1.3292	1.3285	1.3282	1.3260
4	3.0926	3.0904	3.0902	3.0901	3.0895
	5.2281	5.2228	5.2223	5.2220	5.2204
	5.3234	5.3226	5.3226	5.3225	5.3223
	1.3395	1.3298	1.3290	1.3285	1.3260
5	3.0934	3.0906	3.0904	3.0902	3.0895
	5.2303	5.2232	5.2226	5.2223	5.2204
	5.3236	5.3226	5.3226	5.3225	5.3223

Таблица 2

Сходимость МЧО с учетом особенности на ребре для первых четырех Н-волн круглого волновода с тонкими металлическими гребнями в соотношении r ₁/ r ₂ = 0.35, g = 1

N	M					CST Microwave Studio
	10	30	50	80	100
	2.0801	2.0753	2.0744	2.0739	2.0737
1	4.1945	4.1925	4.1921	4.1919	4.1919
	6.2376	6.2265	6.2243	6.2231	6.2226
	8.0234	8.0008	7.9963	7.9938	7.9929
	2.0814	2.0756	2.0746	2.0740	2.0738
2	4.2067	4.2065	4.2065	4.2065	4.2065
	6.2427	6.2282	6.2255	6.2241	6.2236
	8.1233	8.1189	8.1182	8.1178	8.1177
	2.0827	2.0758	2.0746	2.0740	2.0738	2.0680
3	4.2078	4.2073	4.2072	4.2071	4.2071	4.1992
	6.2462	6.2286	6.2257	6.2241	6.2236	6.2046
	8.1355	8.1263	8.1248	8.1240	8.1238	8.0970
	2.0846	2.0759	2.0747	2.0740	2.0738
4	4.2079	4.2073	4.2072	4.2071	4.2071
	6.2509	6.2290	6.2258	6.2242	6.2236
	8.1371	8.1264	8.1248	8.1240	8.1238
	2.0871	2.0762	2.0748	2.0741	2.0738
5	4.2081	4.2073	4.2072	4.2071	4.2071
	6.2577	6.2297	6.2260	6.2242	6.2237
	8.1402	8.1267	8.1249	8.1241	8.1238

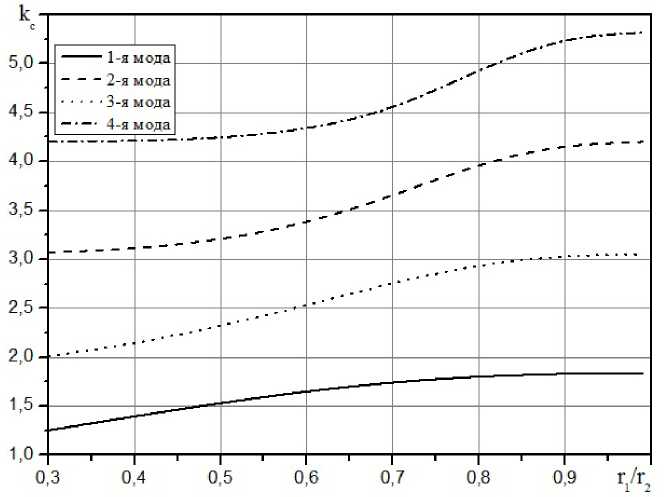
Рис. 3. Зависимость критических волновых чисел первых четырех мод спектра волновода от высоты металлического гребня

Таблица 3

Картины электрического поля первых четырех Н-волн для граничного условия типа электрической стенки ( g = 0)

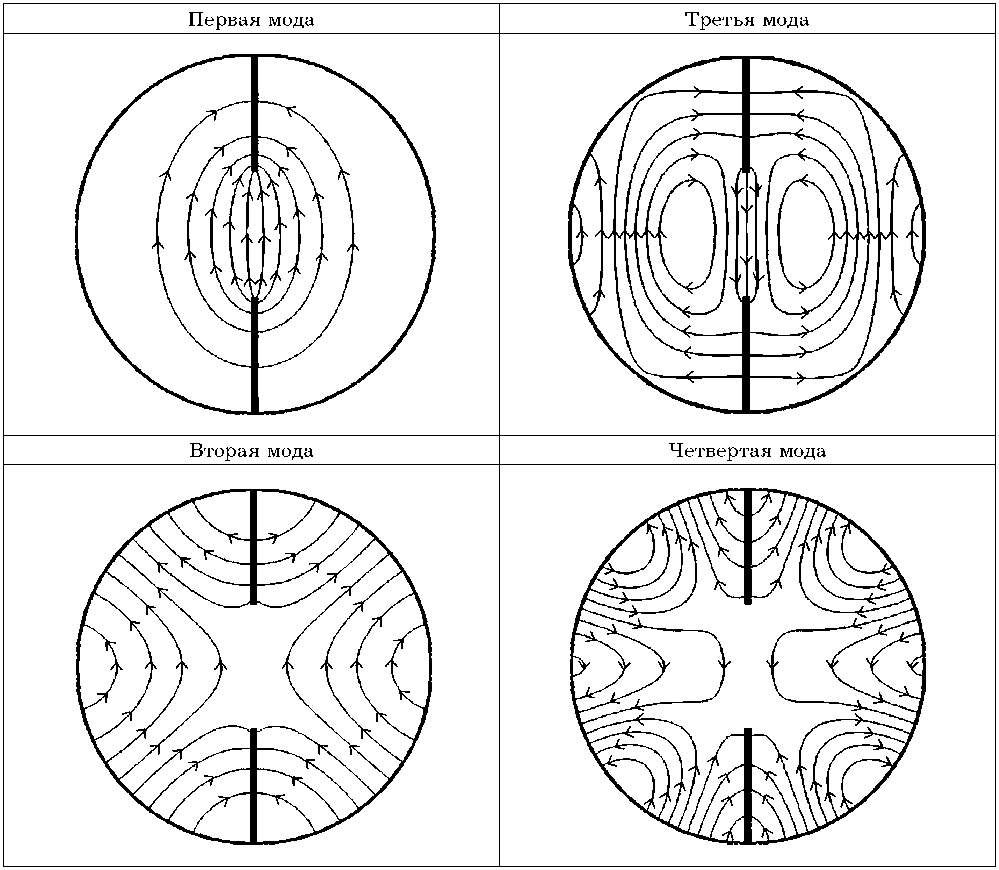
Таблица 4

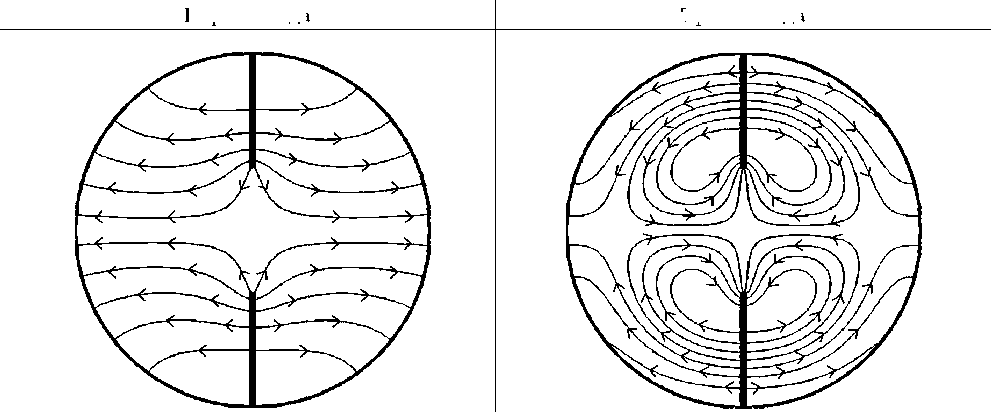
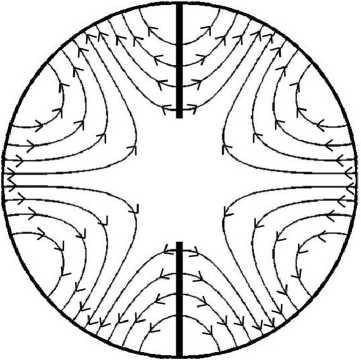
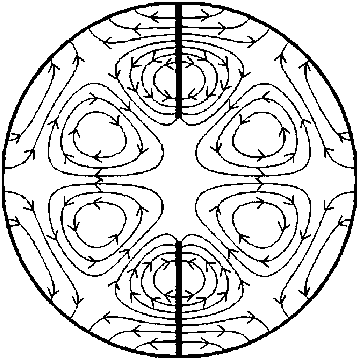
Картины электрического поля первых четырех Н-волн для граничного условия типа магнитной стенки стенки ( g = 1)

Первая мода

Третья мода

Вторая мода

Четвертая мода

чем на 30 %, что позволяет обеспечить соответствующее уменьшение поперечного сечения волновода, сохраняя прежний рабочий диапазон частот.

Результаты визуализации электромагнитных полей в поперечном сечении исследуемого волновода для первых четырех Н-волн с различными граничными условиями представлены в табл. 3 и 4 соответственно. Как было сказано выше, для Н-волн проводилось построение силовых линий электрического поля. Размеры волновода, как и раннее, приняты: r1 / Г2 = 0.35, Ф1 = п /2. Из приведенных результатов видно, что разработанный метод обеспечивают хорошую сшиваемость компонент поля на границе раздела частичных областей. Представленная визуализация подтверждает точность и эффективность предложенных алгоритмов и позволяет проводить анализ влияния металлических ребер на распределения электромагнитного поля в поперечном сечении волновода.

Заключение

Таким образом, в данной работе показано, что применение метода частичных областей с учетом особенности электромагнитного поля на металлических ребрах позволяет строить высокоточные и быстродействующие алгоритмы электродинамического анализа электромагнитных полей круглых волноводов с тонкими радиальными металлическими ребрах. Рассчитанные в явном виде выражения для электромагнитных полей основной и высших типов волн позволяют не только проводить визуализацию их распределения по поперечному сечению волновода, но и строить на их основе алгоритмы расчета эле- ментов и устройств на базе данного типа волновода сложного сечения.

Работа выполнена при финансовой поддержка гранта Президента Российской Федерации МД-118.2017.9.