Электродинамический анализ синусоидальной антенны малых волновых размеров

Последние технологические достижения в области беспроводной связи диктуют необходимость в компактных плоских излучающих структурах. Известно, что первый резонанс тонкого симметричного проволочного вибратора соответствует соотношению 2H /λ≈0,47, где H – длина плеча вибратора, а λ – длина электромагнитной волны. Таким образом, уменьшение размера вибратора соответствует уменьшению приведенного соотношения. Этого можно достичь, придав проводнику синусоидальную форму [1; 2]. Однако несмотря на то, что концепция была разработана в 50-х годах прошлого века [3], изучение внутренних электродинамических процессов в синусоидальных антеннах с помощью строгих электродинамических методов еще предстоит провести, что определяет актуальность данной работы. Исследования для несинусоидальных структур, показали удовлетворительные результаты [4; 5] в плане уменьшения габаритов. Большая часть исследований по синусоидальным излучающим структурам имеет экспериментальный характер, любые ссылки на математическое моделирование были ограничены выводами соответствующих интегралов излучения без строгого решения проблемы рассеяния поверхностных волн на синусоидальной излучающей структуре [6; 7], поэтому обычно приводятся качественные, а не количественные результаты. Ранее в рамках тезисов докладов авторы статьи представили математическую модель синусоидальной антенны и некоторые результаты численного анализа [8]. Настоящая статья представляет

Е^Н © Табаков Д.П., Зондаи В.Ю., 2024

а

б

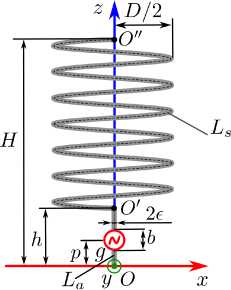
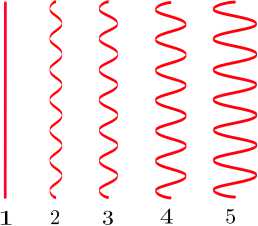
Рис. 1. Тонкопроволочная модель синусоидальной структуры ( а ) и синусоидальный проводник ( б ) при различных соотношениях

D / H = x : 1 — x = 0,0; 2 — X = 0,12; 3 — X = 0,18; 4 — X = 0,24; 5 — x = 0,3

Fig. 1. Thin-wire model of a sinusoidal structure ( a ) and a sinusoidal conductor ( b ) at various ratios D / H = x : 1 — X = 0,0; 2 - x = 0,12; 3 - x = 0,18; 4 — x = 0,24; 5 — x = 0,3

собой расширенную и дополненную версию материалов, опубликованных в [9].

1.    Постановка задачи

Синусоидальная антенна (СА) представляет собой идеальный проводник OO ′′ круглого сечения, имеющий прямолинейный ОО‘ и синусоидальный участки О ‘ О ", расположенный над бесконечно протяженным идеальным экраном, лежащим в плоскости XOZ . Радиус проводника равен 8 . Геометрия СА показана на рис. 1, а . Здесь D - ширина синусоидального участка; H – общая осевая длина излучателя; h – длина прямолинейного участка ОО ‘ . Прямолинейный участок ОО ‘ имеет разрыв длиной b , центр которого соответствует z = p, при этом переменную p в дальнейшем будем называть линейной координатой точки питания. В разрыв помещен генератор ЭДС g , являющийся источником стороннего электрического поля на проводнике. Под действием стороннего электрического поля на проводнике возникает поверхностный электрический ток, распределение которого удовлетворяет уравнениям Максвелла, граничным условиям и условию излучения на бесконечности. Полагая, что b ^ X , где X - длина волны, будем считать, что распределение поверхностного тока непрерывно в области зазора. Условие 8 <  X позволяет нам использовать тонкопроволочное приближение, в рамках которого можно перейти от поверхностной плотности тока к полному азимутально-независимому осевому току I ( l ), где l - ествественная координата на образующей L проводника ОО ". Далее также будем использовать условие h <  H , минимизирующее влияние прямолинейного участка OO ′ на общее распределение тока.

Образующие участков проводника могут быть определены следующим образом:

L a :    r ( l ) = z l , l g [0; h ];

Ls : r(t) = x(D/2)cost + z(h + hz(t-n/2)), t∈2πNl[0;1]+π/2.

Здесь переменная l является естественным параметром на образующей прямолинейного участка L a ; переменная t - параметр на образующей синусоидального участка; h_z представляет собой коэффициент развертки синусоидального элемента вдоль оси z ; N_l – число периодов синусоиды. Общую образующую обозначим как L : L a о L s , l g [0; L ], где l g [0; h ] соответствует L a , а l g [ h ; L ] соответствует L_s . При этом для L_s осуществляется процедура репараметризации [9] с целью перехода от параметра t к параметру l для L_s в (1). Точка О ‘ является особой точкой на общей образующей, так как в ней вектор касательной изменяется скачкообразно. Данный момент необходимо учесть в дальнейшем при осуществлении процедуры сегментации общей образующей.

В рамках тонкопроволочного приближения мы можем описать электромагнитное поле (ЭМП) структуры интегральным представлением [12], записанным с учетом наличия бесконечно протя- женного экрана:

F ( r )= ∫ I ( l ′ ) K ^{( F )}( r , r ( l ′ )) dl ′ , F ≡ E , H ;

Здесь

K ^{( F )}( r , r ( l ′ ))=₂ ¹ ( K ^{( F )}( r , r ( l ′ )) - K ^{( F )}( r , r ( l ′ )) )

– ядра ИП ЭМП; r ( l ) – радиус-вектор на зеркально отображенной общей образующей L , полученной заменой z →- z в (1):

K ( E ) = W m^ k 2 G + A ( d B)   K ( H ) =( d _x l ') B;

ik              dl ‘ ik

l ' = d r ( l ') / dl = l ( l ') - единичный вектор касательной на L , вычисленный в точке, соответствующей значению натурального параметра l ';

• 1    e ^{— ikR}        1 dG    ikR + 1

G =        , B =      = — G

4n R      RdR _R ²

– соответственно функция Грина и ее производная; R = ^| d |² +s ² - регуляризированное расстояние между точкой источника r ( l ') и точкой наблюдения r ; d = r — r ( l '); W m и k - волновое сопротивление и волновое число свободного пространства соответственно; r – точка наблюдения. Бесконечно протяженный идеальный экран в плоскости XOY , по сути, представляет собой «электрическую стенку», на которой выполняются условия E x = E y =

= H z =0. С помощью граничного условия

l ( l ) ■ ( E ^(ln)( r ( l )) + E ( r ( l ))) = 0, l g L ,

в котором E ⁽ⁱⁿ ) - поле, создаваемое сторонними источниками, E – поле, создаваемое токовой функцией I ( l ) согласно (2), можно получить интегральное уравнение Фредгольма первого рода

I ( l ') K ( l , l’)dl' = E ( l ), l g L , L

в котором E ( l ) = l ( l ) ■ E ⁽ⁱⁿ ) ( r ( l )) - правая часть, представляющая собой касательную составляющую электрического поля на образующей. K ( l , l ') = = l ( l ) ■ K ^{( E} ) ( r ( l ), r ( l ')) - ядро ИУ.

Функция E ( l ) равна нулю всюду, за исключением области зазора, и может быть задана следующим образом:

( l )= [ u / b , l g [ p — b /2; p + b /2];

• 1    0, l £ [ p — b /2; p + b /2],

где U – напряжение генератора в области зазора, при численном моделировании предполагалось, что U = 1 В.

Для перехода от ИУ (4) к СЛАУ аппроксимируем образующую L ломаной L ⁽ N ’ , состоящей из N = N a + N s сегментов и, соответственно, N + 1 узлов:

( N )

L 7 L : Г 1 , r 2

, r N + 1, ^ , r N + 1 ^. a

Здесь Na соответствует числу сегментов на прямолинейном участке, Ns – числу сегментов на синусоидальном участке, узел rN +1 - особой точке О‘ образующей L. Между узлами с номерами k и k +1 находится к-й сегмент rk (l), урав- нение которого может быть записано в следующем виде:

r k ^{( l} ) = r k + ¹ k^l , ^{l g [ —Л} k ^{/2, Л} k ^/2].

Здесь r * =( r k + r k _{+ 1})/2 - центр сегмента; Л k = = ¹ r k + 1 ^— r k ^{1 -} длина ^{сегмента}; ¹ k = ^{( r} k + 1 ^— r k )/ ^Л k ^-единичный вектор касательной на сегменте, здесь и далее индексы k = 1...N будем ассоциировать с сегментами на соответствующем элементе структуры.

Полагая, что Л i ^ X , и I ( l ') = I^ g Л i , на основе (4) можно получить СЛАУ вида

ZI = E ,                                                  (5)

где Z - матрица СЛАУ, элементы Z ij которой определяются выражением

Z i , j = l i 1 K ( E ’ (^ Г■ ( l )) dl ,

Л j в котором I - вектор, содержащий значения комплексных амплитуд токов Ij на сегментах; E – вектор, содержащий информацию о стороннем поле в точках коллокации, элементы Ei которого вычисляются следующим образом: Ei = 1 i ■ E(in’(ri). Ранее приведенные выражения с успехом использовались для решения задач излучения и дифракции электромагнитных волн [11; 12].

2.    Численное моделирование и анализ результатов

Были исследованы пять вариантов синусоидальной структуры, показанных на рис. 1, б . Отметим, что первый вариант соответствует обычному электрическому вибратору с длиной плеча, равному H . Для всех вариантов h / H =0,06, b / H =0,012, при этом для обоих проводников s / H = 1,8 ■ 10 ^— 3 . Число сегментов синусоидального проводника для вариантов 1–5 структуры было равно 79, 132, 175, 220 и 280 соответственно и подбиралось, исходя из условия близости длин сегментов синусоидального проводника к длинам сегментов активного прямолинейного проводника. Число сегментов активного проводника было равным 5. При этом выполнялось условие 2 s < Л <  12 s [6], необходимое для получения устойчивого решения ИУ (4). В диапазоне H / X = x = [0,001;0,6] вычислены распределения токов по образующей структуры, и далее на основе этих распределений определены характеристики излучения и зависимости входного сопротивления структуры от x .

0.1 0.12 0.14 0.16 0.18 0.2 0.22 0.24 H/X

а

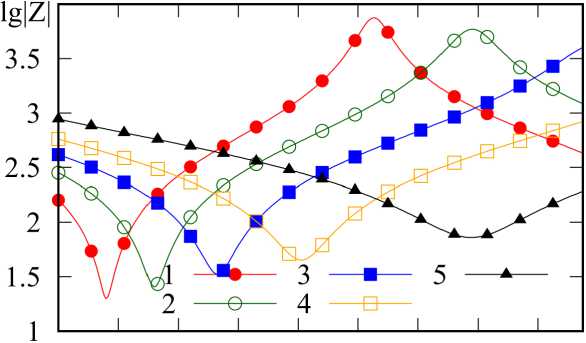
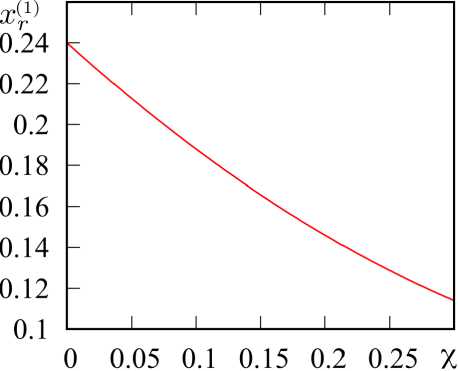
Рис. 2. Зависимость входного сопротивления от x при различных значениях х ^: 1 — X = 0,3; 2 — X = 0,24; 3 — X = 0,18; 4 — X = 0,12; 5 – χ =0 ( а ); зависимость частоты первого резонанса от χ ( б )

Fig. 2. Dependence of input resistance on x for different values of x ^: 1 — X = 0,3; 2 — X = 0,24; 3 — X = 0,18; 4 — X = 0,12; 5 — X = 0 ( а ); dependence of the first resonance frequency on χ ( b )

б

Расчет характеристик излучения показал, что практически во всем исследуемом диапазоне диаграммы направленности для всех вариантов структур имеют довольно мало отличий от диаграммы направленности обычного симметричного электрического вибратора аналогичных размеров. Наибольшие отличия возникают только вблизи верхней границы исследуемого диапазона, и для этого графики случая будут приведены далее. То же касается и распределений тока вдоль образующей проводника, имеющего в рассмотренном диапазоне вид стоячей волны. Соответствующие результаты, полученные в окрестности первого резонанса, приведены в [8].

Наиболее интересным с практической точки зрения является исследование частотной зависимости входного сопротивления. Зависимость модуля входного сопротивления | Z | от x = H / X для различных вариантов синусоидальной структуры проиллюстрирована на рис. 2, а . Здесь для вариантов 1 и 2 можно наблюдать резонанс напряжений (минимум | Z |) и резонанс токов (максимум | Z |). Для остальных вариантов на графике можно видеть только резонанс напряжений. Графики показывают, что увеличение ширины структуры в заданных пределах позволяет снизить частоту первого резонанса и, соответственно, уменьшить габариты структуры более чем в два раза. Зависимость резонансной частоты x ⁽ _r ¹⁾ от χ показана на рис. 2, б . Она может быть аппроксимирована квадратичной функцией:

x ™(% ) « 0,24 - 0,57 % + 0, 50 x ² . (6)

Проследим за тем, что происходит с резонансым значением сопротивления R r и добротностью резонанса Q с ростом X . Для анализа и последующей оценки добротности используем условие Z_b / Z_r =

= V2, в котором Z r = | Z ( x r )|, Z b = | Z ( x r +Д x /2)|; Д x - ширина полосы частот, обеспечивающая указанное условие (в силу симметрии | Z ( x_r -∆ x /2) | = = | Z ( x r + Д x /2) |). При этом добротность резонанса можно вычислить как Q = x r / Д x .

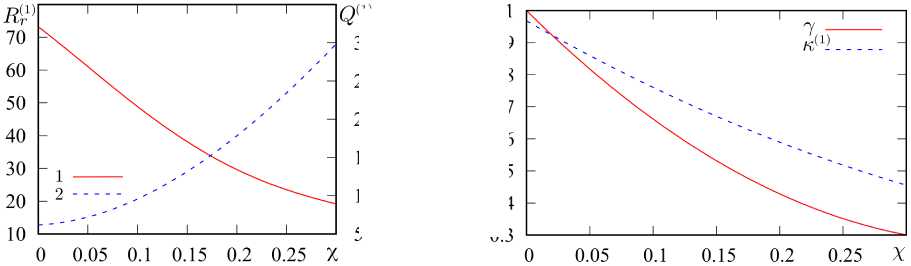
Зависимости входного сопротивления R_r ⁽¹⁾ и добротности Q ⁽¹⁾ от χ проиллюстрированы на рис. 3, а . Здесь видно, что входное сопротивление уменьшается с ростом χ более чем в три раза для исследуемого диапазона, а добротность резонанса - возрастает примерно в шесть раз. Зависимости R ^) и Q (1) от X могут быть аппроксимированы следующим образом:

R Xx) » 73,2 — 230, 8 x- (7) - 403, 6 % ² + 3211, 2 % ³ - 4342 X 4 ;

Q ⁽¹’ ( X ) « 5,7 + 6, 1 x + 298,1 % ² - 185 % ³. (8)

Добротность Q прямо пропорциональна количеству энергии, запасаемой в ближней зоне излучающей структуры, и обратно пропорциональна энергии излучения. В свою очередь, мощность излучения на резонансной частоте определяется выражением P a = U 2 / R r , где U - напряжение в точке питания. Таким образом, в точке первого резонанса с ростом χ увеличивается мощность излучения структуры и растет количество энергии, запасаемой в ее ближней зоне.

На рис. 3, б показаны вычисленные и аппроксимированные зависимости коэффициента замедления κ ⁽¹⁾ ( χ ) ≈ 4 x ⁽ _r ¹⁾ ( χ ) и коэффициента укорочения проводника структуры y ( % ) = L (0)/ L ( % ). Последнюю зависимость можно аппроксимировать следующим образом:

• Y ( x ) = 1 - 3,91 % + 5,26 % ².

Фазовая скорость v волны тока, распространяющейся вдоль проводника, может быть определена

?(1)	1
30	0.9
25	0.8
20 15	0.7 0.6 0.5
10	0.4
5	0.3

а

б

Рис. 3. Зависимости R_r ⁽¹⁾ (1) и Q ⁽¹⁾ (2) от χ ( а ); зависимости коэффициента замедления κ ⁽¹⁾ и коэффициента уменьшения электрической длины γ от χ ( б )

Fig. 3. Dependences of R_r ⁽¹⁾ (1) and Q ⁽¹⁾ (2) on χ ( a ); dependence of the retardation coefficient κ ⁽¹⁾ and the coefficient of reduction of the electrical length γ on χ ( b )

Win

0.5 и--------1--------1--------1--------1--------1--------1--------

~ 0.2  0.25  0.3  0.35  0.4  0.45  0.5 H/X

а

б

Рис. 4. Зависимость входного сопротивления от x при различных значениях х : 1 — X = 0,3; 2 - X = 0,24; 3 — X = 0,18; 4 — X = 0,12; 5 – χ =0 ( а ); зависимость частоты второго резонанса от χ ( б )

Fig. 4. Dependence of input resistance on x for different values of X ^: 1 — X = 0,3; 2 — X = 0,24; 3 — X = 0,18; 4 - X = 0,12; 5 — X = 0 ( a ); dependence of the second resonance frequency on χ ( b )

а

б

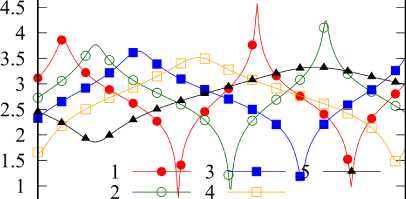
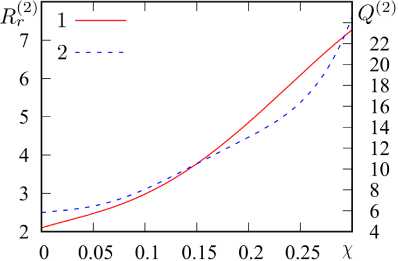
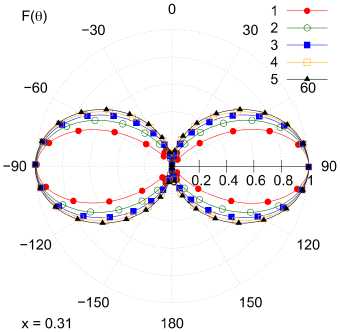
Рис. 5. Зависимости R ² ) [кОм] и Q (2) от x ( а ), диаграмма направленности ( б) при x = 0,31: 1 - x = 0,3; 2 — X = 0,24; 3 - x = 0,18; 4 - x = 0,12; 5 - X = 0

Fig. 5. Dependences of R ^ ² ) [kOhm] and Q ^²⁾ on x ( a ), radiation pattern ( b ) at x = 0,31: 1 - x = 0,3; 2 - X = 0,24; 3 - x = 0,18; 4 - X = 0,12;

5 – χ =0

как v = ck(x)/ y(X)• Уже при X > 0,0259 значение v превышает скорость света c. Это говорит о том, что с объектом, формирующим поле структуры, следует ассоциировать стоячую поверхностную волну, представляющую собой суперпозицию прямой и обратной поверхностных волн, распространяющихся вдоль синусоидального элемента со скоростью и = кс и поддерживаемых им даже при столь малых волновых размерах излучающей структуры. Распределение тока, фигурирующее в

ИУ (4), можно рассматривать как «проекцию» стоячей поверхностной волны на образующую проводника. График y ( x ) , представленный на рис. 3, б , показывает, что синусоидальная антенна может замедлять скорость поверхностных электромагнитных волн до 50 % от скорости света в свободном пространстве для структур значительной ширины. Аналогичная цифра справедлива и по отношению к уменьшению габаритов излучающей структуры.

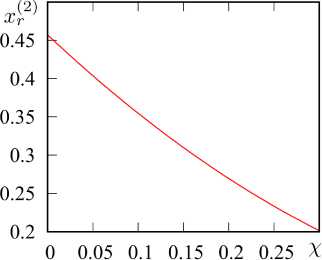
Далее рассмотрим результаты расчета для случая второго резонанса. Частотные зависимости входного сопротивления структуры при различных значениях χ приведены на рис. 4, а , а зависимость частоты второго резонанса от χ – на рис. 4, б . Видно, что, в отличие от случая первого резонанса, с ростом χ входное сопротивление структуры увеличивается, достигая 10 кОм, а резонансная частота снижается, как и в случае первого резонанса, однако здесь это снижение происходит немного медленнее. Добротность, как показывает рис. 5, а , также возрастает. Зависимости R' ² , Q ⁽²⁾ и x_r ⁽²⁾ от χ могут быть аппроксимированы следующим образом:

R(2)(X) * (2,10 - 8,28Х — 42,5X2 +

+ 632 x 3 — 1627 X 4 + 187 X 5 ) • 10 3 ;

Q(2)(x) * 5,83 +12,1X —199,4X2 +

+ 5499, 6 x ³ - 30042,2 X 4 + 52632,8 X 5 ;

x(,2)(x) * 0,457 -1,11X + 0,857X2 •

Заключение

В статье представлена математическая модель синусоидальной антенны, построенная на основе тонкопроволочного интегрального представления электромагнитного поля. Внутренняя задача сформулирована в виде интегрального уравнения Фредгольма первого рода. Следует отметить, что полученная математическая модель структуры позволяет осуществлять электродинамический анализ в довольно широкой полосе частот, однако в данной статье рассматривается случай относительно малых волновых размеров структуры, при которых распределение тока вдоль образующей проводника имеет вид стоячей волны.

Проведено численное моделирование, включающее расчет токовых функций, входного сопротивления и диаграмм направленности при малых волновых размерах структуры, а также при различных вариантах геометрических параметров. Исследования проведены для частот, соответствующих областям первого и второго резонансов входного сопротивления. В результате численного моделирования было выявлено, что увеличение ширины синусоидального элемента ведет к смещению резонансов в область более низких частот, однако при этом растет добротность резонансов. С практической точки зрения использование рассмотренной структуры позволяет существенно уменьшить габариты в сравнении с тонким электрическим вибратором, однако при этом будет соответствующим образом сужен рабочий диапазон, определяющийся, в силу слабой зависимости характеристик излучения от частоты, добротностью резонансов. В работе на основе результатов численного моделирования дана интепретация решения внутренней электродинамической задачи, согласно которой стоячая волна тока на образующей спирального проводника представляет собой суперпозицию прямой и обратной бегущих волн, фазовая скорость которых больше скорости света. При этом стоячая волна тока является «проекцией» стоячей поверхностной волны, образующейся в плоскости синусоидального проводника. Стоячая поверхностная волна, в свою очередь, образуется в результате суперпозиции прямой и обратной поверхностных (замедленных) волн, распространяющихся со скоростью, существенно меньшей скорости света. Коэффициент замедления этих волн можно оценить по величине смещения резонансов. В дальнейшем авторы планируют уточнить физику происходящих в структуре процессов, используя спектральный анализ токовых функций и исследование распределений электромагнитного поля в ближней зоне структуры, а также получить аналогичные результаты для структур с близкой геометрией.