Электродинамический анализ зеркальных антенн в приближении барицентрического метода

Разработке методов, способов и алгоритмов анализа электромагнитных характеристик зеркальных антенн (ЗА) посвящено большое количество работ [1–6]. Основу электродинамического анализа ЗА составляет решение внутренней задачи электродинамики, которое выполняется в приближении Кирхгофа [1; 2; 6] или при непосредственном исследовании интегральных/интегро-дифферен-циальных уравнений [3–5]. На приближении Кирхгофа основываются асимптотические методы, достоинство которых состоит в невысоких вычислительных и емкостных затратах формируемого алгоритма. Их существенный недостаток – низкая универсальность при анализе многоэлементных ЗА с отражающими и облучающими устройствами сложной геометрической формы при относительно невысокой точности [17]. Этот недостаток с учетом стремительного развития средств вычислительной техники и технологий параллельных вычислений устраняется при численном решении интегро-дифференциальных уравнений электродинамической теории ЗА [4]. Основу численного решения составляет проекционная постановка метода Галеркина и его модификаций (метод моментов [7]). При этом вычислительная эффективность формируемой численной схемы существенным образом определяется рациональностью выбора си- стемы базисных функций, относительно которой задается разложение искомой функции плотности тока. Для решения указанной задачи в работе [8] при анализе ЗА предлагается использовать барицентрический метод (БМ) [9; 10]. Недостатки [8] состоят в том, что постановка задачи дифракции и интегральное представление электромагнитного поля (ЭМП) отличаются от классически принятых [11] для ЗА [4]; базисные функции вычислительно избыточно формируются через дифференциальные формы Уитни (краевые векторные функции Неделека). Также в работе [8] в явном виде не приводятся результаты сравнений по эффективности решения тестовых задач с широко используемым в современных САПР электродинамического анализа антенн и СВЧ-устройств методом формирования базисных функций – RWG [12]. Цель настоящей статья во взаимосвязи с результатами [10; 13] состоит в устранении указанных недостатков.

1 . Постановка задачи дифракции

Задачу электродинамического анализа ЗА сформулируем в классическом представлении за- дачи дифракции электромагнитной волны на системе бесконечно тонких идеально проводящих экранов [4; 11].

Зеркальную антенну представим объединени-

M ' ем ^S = U ^S s s = 1

конечного числа M' связных ори-

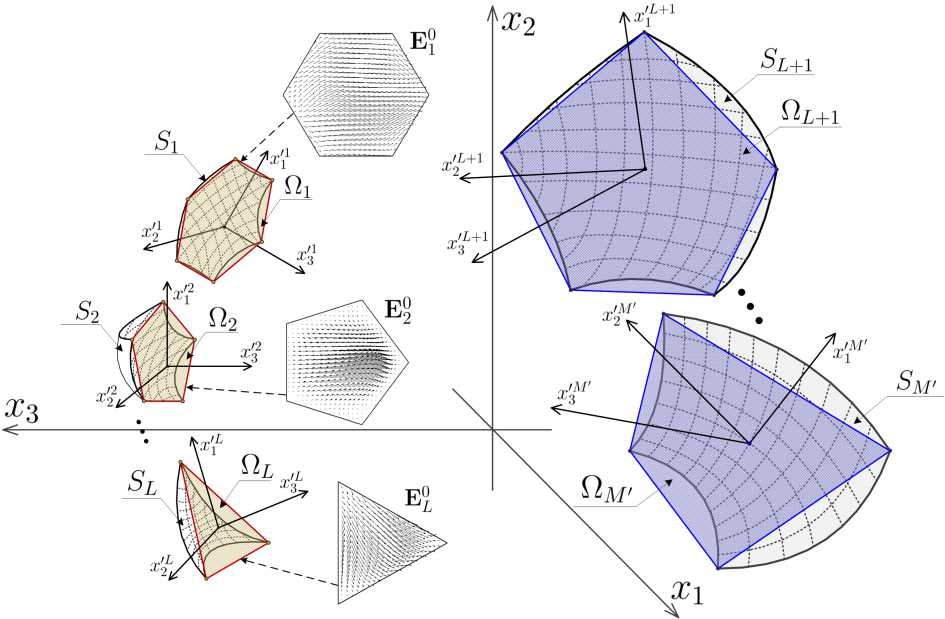
Рис. 1. Геометрическое представление зеркальной антенны

Fig. 1. Geometric representation of a reflector antenna

ентированных незамкнутых и непересекающих-ся Ssp|Ss, = 0 (s, s'е {1, M'}, s ^ s') поверхностей класса С” в R3, которые определяются L < M‘ облучателями и M'- L рефлекторами (рис. 1). Край дSs = Ss \ Ss поверхности Ss представляется кусочно-гладкой кривой без точек самопересече-м'                           ____ ния; дS = |JdSs . Раскрыв Qs (s = 1, M') поверх-s=1

ности S_s зададим многоугольником с числом N_s

Vx H = - i p E ;    Vx E = i p H ,   x е R ³ \ S ;

^E t S = ^E 0 S -    ^E 0 S е C ” ( S ) ;    E , H е L ^ ( ^{r 3} ) ;

E , H = o ( r ¹ ) , r

|x| ^да при Im P> 0;

H x e r - E = o ( r ¹ ) , E x e _r + H = o ( r ¹ ) , E , H = O ( r ^{- 1} ) , r ^да при Im P = 0,

вершин P 1 ^s ,..., P ^

относительно соответствующей

системы координат x ‘ ^s

= { x 1 ^s , x 2 ^s , x 3 ^s } . Внешние

источники ЭМП устанавливаются в раскрывах □ 1 , Q 2 ,..., Q l облучателей исходно заданным распределением напряженностей электрических полей E 0 = { e ⁰ , E 0 ,..., e L } соответственно. Кривизна S характеризуется орт-вектором нормали í . Предполагается, что поле облучателей E 0 является монохроматическим, а S располагается в среде

где M ^ и м - - внешность и внутренность замкнутой связной ориентированной поверхности M е R ³ класса С ^да с конечным числом компонент связности при S с M ; e r = x/|x| ; Р 2 = = ш ² p^£ + i am^{- 1} ] , Im p> 0, P^ 0; ю - угловая частота; S _§ : = { x : |x - y| <5 , y е s } ; 6> 0; индекс т обозначает тангенциальную составляющую поля на S .

Доказательство существования и единственности решения задачи (1), (2) известно из [11], которое

с постоянными электромагнитными параметрами ( e , p a ) .

Следуя [11] и учитывая содержательное описание, сведем обобщенную постановку задачи дифракции E ⁰ на S к определению рассеянного ЭМП: E , H е C ² ( R ³ \ S )Q C (R \ дS ₅)Q C ( M - \ дS ₅) ,    (1)

5> 0              5> 0

удовлетворяющего [11]:

определяется в виде векторного потенциала:

Cu = f, где

C u = VЛ ( V- u ) + p ² Л и ; f = i p eT| ;

Д и ( x ) = J V ( x , y ) u ( y ) d y ,

S x = {x1,x2,x3}еS; u(y)-v(y) =0

при y e S ; u имеет смысл плотности тока на S ;

^ ( х , у ) =

1 _е ^; Р|^{х -}у| 4п |х - у|

– функция Грина.

Барицентрический метод предполагает численное решение (3) при задании аппроксимаций Н us (x) = Уcpуp (x) (Cj - коэффициенты разложе-7 =1

ния) искомой плотности тока us на Ss (s = 1, M‘) в системе базисных функций уp (x )e С (Sp), которые являются глобальными относительно Sp и форми- s [13]:

p s /

руются из у h (^х), V e (x) j e M_p , j^s e M' j s

V h (x) = -v ^s (x) ^x   У a h  'V h (x) ;

j          -—s))¹

j ' ^s e M p_p

Ve (x) = vs (x)x У ae  уe (x), js                                                         js j's j's j's eMp

где

^V j s ( ^x ) = ® s ^V 2 * ^s • s ( ^x ) ; v e i ( ^x ) = ® s ^v 2 Ф ^p , s ( ^x ) ;

® s

= {

- матрица преобразования координат из x ’ ^s '■1 s , x 2 s , x з ’ } в ^x = ^{ x i , x 2 , x з }^;

v‘ =L—,—, 0 p ;

• ²    [a x 2 ’a< J’

  ^V 2 =

  
  

  ,       , o | ;

  [a x i ax 2

  
  

  j^s [« n ( x ) j

  
  

• 2.    Интегральное представление электромагнитного поля зеркальных антенн в приближении барицентрического метода

N s - 1 ^ф s ■ s ^{( x} ) = P s ^! П n = 0

1's n

ah и ae - j's-е и j's-е элементы 7 s -го и 7-го jj. s        jsj -s      >           >                         >             > соответствующих собственных векторов матриц

Ah,e =[bh,e j Ch,e при составлении Вh,e и Ch,e из численного решения БМ [9] относительно Qs задач Неймана и Дирихле для однородного уравнения Гельмгольца; £П(x) — n-е барицентрические координаты, заданные с учетом [14] для Qs с К2 относительно системы координат x’s = = {x 1s, x2s, x3s} в плоскости x3s = 0; ps - порядок аппроксимации для Ss; Mps и Ms - множества мультииндексов, правила формирования которых определены в [13].

Заданная постановка задачи дифракции относительно ЗА и предложение об аппроксимации u ^s (х) = У C h V ^h (х) + У c^e у e (х) ^ss            j^sj^s

7s eM ps j j        js eM Ps определяют представление исходного интегро-дифференциального уравнения (3) в виде следующей системы из s уравнений:

M '

y ^[v j ^ ( ^х , у ) V- u ^s ' ( у ) d у

+

s '= 1

^S s 2

+ P ² jy ^х , у ) u ^s '⁽ у ) 1= ^f s ^{( х} ) , ^S s '                              _

^{где x e S} s ; ^f s = i p ^E 0 S

^; E0I S

s 0

= - v x E - танген-

Ss

s

циальная составляющая электрического поля, наведенного полями источников {E0, E2,

• ••

, E L }

в точке x e S_s . Поле e S из { E 0 , E 0

, •••,

E 0L } опреде-

ляется, исходя из принципа Гюйгенса – Френеля [1]: E S s ( x ) =

= 4 п

L

^: E j |E ⁰ ( у )| E ⁰ ( ^х , у ) ^ ( ^х , у ) ^а х , у d у ,

l = 1 S ,

l

где

^{E 0} ( ^х , у ) = ^{E 0} ( ^х , у )/ |^{E 0} ( ^х , у )|;

E ⁰ ( ^х , у ) = H ⁰ ( ^х , у ) ^x d ( ^х , у ) ;

H ⁰ ( ^х , у ) = !H ⁰ ( ^х , у )/ ^ ⁰ ( ^х , у )|;

d ( ^х , у ) = ( ^{х -} у )/ |^{х -} у| ;

^{lH 0} ( ^х , у ) = ^d ( ^х , у ) ^x E 0 ( у ) ;

E 2 0 ( у ) = E 0 ( у )/ |^Е 0 ( у ) ;

а _ху e [ 0; 1 ] - устанавливает наличие эйконала между точками x и у .

Подстановка аппроксимации u ^s ( х ) в (4) с учетом свойства [13] базисных функций (6), второй формулы Грина и свойства дифференциальных операторов [11] сводит интегральное представление ЭМП ЗА в приближении барицентрического

M ' /   „           \

E l ~s ___

I Mi Ps + M

метода к системе из

линейных

s ps

s=1                  s алгебраических уравнений относительно неиз-

:e^s : j^s

вестных коэффициентов разложения c h , C j^s

[ f . ( ^X ) V h‘‘ . ( ^X ) d ^X =

S s ^j

M '

= z J z c h . ‘ j- v - . ( x )

. '= 1      . '       ' j                   j

X

S '= 1

j e M p.,

S

s

X J V-Vh,s. (yMx,y)dydX- s.'        j

- P2 J Vh (X) J V^, (y)^(X,y)dydX s. j         Ss, j

• 1:    function GenPerm(W,p)

• 2:    М = N + р - 1;

• 3:     for т = 0 to М — 1 do

• 4:        if т < N — 1 then l_m = О

• 5:          else l_m = 1

• 6:     Lp 4= I

• 7:     while NextSet(Z,A/) do L_p 4= I

• 8:      return L_p

+

+ У c e j , j ' . e ^M p. ,

,. ’ _f^V-V h . ^{( x} ) . j

S

s

X

Рис. 2. Псевдокод алгоритма генерации перестановок 1 и 0 в последовательности l e L p длины N + p - 1 с p единицами и N - 1 нулями

Fig. 2. Pseudocode of the algorithm for generating permutations 1 and 0 in a sequence l e L _p of length N + p - 1 with p ones and N - 1 zeros

X J v-v «■ (y )^(X, y) dydX - ss

• ^- P ² J v ^h ( ^X ) J v e C ( y ) ^ ( x y ) d y d ^X . ;

• 3. Особенности алгоритмической реализации и результаты верификации сформированных решений

^s . j         ^s .'                                    J.

j ^f . ( ^X )v e . ( ^X ) d ^X =

j

S s

Вычислительные особенности исследования со-

M '

= £ J Z c h.. J^v-v ' . ( ^x ) s ' =11 -' . TT ' j

X

s ,= 1

j e M p.,

S

s

X J ^V- V - ,r ( y ) ^ ( X , y ) d y d X s . ,         j

-

отношений вида (7) при алгоритмической реализации БМ рассмотрены в [13]. Их основу состав л яют правила задания множеств мультииндексов M p и

M p , формируемых из ГЙ p :

•W            I          / ^*    ^*          ^*           ^*         X ^*

^M p =1 j = ⁽ j 0 , ^j1,..., ^j n ,..., ^j N - 1 ) ^{: j} n ^e ^ + ,

X                                                      (8)

-

P2 J Ve. (x) J Vh, (y)^(Xy)dyd s., j

S

s

+ У c e

M ,  j''

j ' ' e M p. ,

. J^{V- V} j ( x ^)X _ ^s .

x

+

j n = ^p f , n e[ 0; N - 1 ]         J

где p e N ;

I^M p l

f ^{N +} p - 4 p

z ₊ = n ^ { 0 } ;

X J ^У^ (y)^(X,y)dydX- s.

-P2 Jve. (X) J Ve., (yMXy)dydX .• s. j        s’    j                               l|

Относительно соотношений (7) следует отметить, что если экран Ss является плоским, то V-ve. (x) = 0. Интегралы в (7) вычисляются численно [15] при разбиении S. на треугольные элементы при построении триангуляции Делоне и последующим использованием кубатурных формул интегрирования по треугольным областям. Способ исключения появления сингулярности в Т(x, y) сводится к разнесению узловых точек интегрирования относительно x и y для смежных треугольников и переходу в полярную систему координат при расположении x и y в одной треугольной области [13].

N - число вершин Q .

Уточним, что правило (8) порождения РИp сводится к алгоритму генерации композиций неотрицательных целых чисел j = (j,Д,...,jn,...,N-1) числа p при интерпретации / (M = N + p -1) разрядным числом l = (10,11,...,lm,...,Im-1) из единиц и нулей (lm e |^0; 1]). Набор элементов l составляет множество Lp, формируемое расстановкой 1 и 0 длины N + p -1 при условии наличия в l e Lp p единиц и N -1 нулей. Алгоритм формирования

L _p основывается на алгоритме генерации перестановок 1 и 0 (рис. 2).

В алгоритме на рис. 2 функция NEXTSET задает новую перестановку l e L _p при определении возможности ее формирования (рис. 3).

Последующий перевод l из сформированного множества L p в j производится суммированием элементов l_m справа налево. При этом значение

• 1:    function NextSet(Z,M)

• 2:     г = M — 2

• 3:      while (г ^ —1) Л (7,- ^ 1ц i) do i = г — 1

• 4:      if г = — 1 then return false

• 5:     к = M - 1

• 6:      while Li ^ Ik do к = к — 1

• 7:     SWAP(Z,i,fc)

• 8:      i = i + 1

• 9:     к = M — 1

• 10:      while i < к; do

• 11:           г = г + 1

• 12:         к = к - 1

• 13:          SWAP(Z,z,/c)

• 14:      return true

Рис. 3. Псевдокод функции NEXTSET

Fig. 3. Pseudocode of the NEXTSET function элемента jn составляет непрерываемая нулями сумма последовательности единиц из l. В случае если элемент lm равен нулю, то соответсвующее последующее значение jn+1 приравнивается к нулю. Алгоритм перевода бинарной последовательности l в мультииндекс j приведен на рис. 4. В представленом алгоритме предполагается, что исходно элементы мультииндекса j равны нулю.

Сравнительные графики зависимости количества процессорных тактов ( Q ) от размера входных данных ( N , p ) генерации M p при использовании предложенного алгоритма и при полном переборе приведены на рис. 5.

Полученные результаты (рис. 5) наглядно демонстрируют вычислительную предпочтительность предложенного алгоритма, позволяющего достаточно оперативно (время вычислений для ПЭВМ с процессором Intel(R) Core(TM) i7-3612QM CPU 2.10 GHz для N = 24, p = 10 при программной реализации на Visual Studio C++ с использованием библиотеки для работы с векторами и матрицами armadillo не превышает 8 с) формировать множество мультииндексов M p .

Для наглядной демонстрации предпочтительности применения БМ в решении задачи электродинамического анализа ЗА в сравнении с известными методами [7; 12; 16], предполагающими аппроксимацию u ⁵ ( x ) базисными функциями RWG, проведем апостериорное исследование при реализации вычислительных экспериментов на пяти тестовых задачах. Первая, вторая и третья состоят в определении u на плоских бесконечно тонких идеально проводящих прямоугольных экранах S 1 , S 2 и S 3 размерами XxX , 3 Xx 3X и

• 1:    function Conv!nd(ZJ, М)

• 2:     П = 0

• 3:     for m = М — 1 downto 0 do

• 4:        if l_m = 0 then n = n + 1

• 5:         else j_n = j_n + 1

• 6:      return true

Рис. 4. Псевдокод алгоритма перевода l в j

Fig. 4. Pseudocode of the algorithm for translating l to j

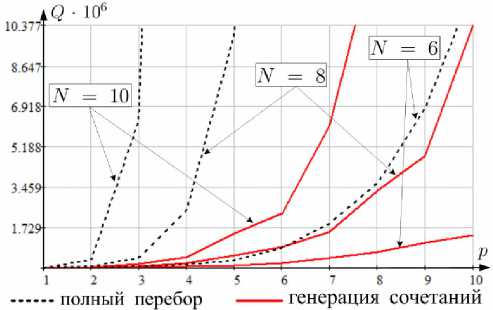
Рис. 5. Сравнительная зависимость Q от N , p для разработанного алгоритма и алгоритма полного перебора

Fig. 5. Comparative dependence of Q on N , p for the developed algorithm and the exhaustive search algorithmа

5Xx5X соответственно ( X - длина волны). Суть четвертой тестовой задачи составляет вычисление u на плоском бесконечно тонком идеально проводящем экране S 4 , заданного П-образной областью из восьми вершин:

P 0 = ( - 0,31 X ; - 0,712 X ; 0 ) , P 1 = ( - 0,31 X ; 0, 337X; 0 ) ,

Р ₂ = ( 0,31 X ; - 0, 337X; 0 ) , P 3 = ( 0,31 X ; - 0,712 X ; 0 ) ,

P 4 = ( 2 X ; - 0,712 X ; 0 ) , P 5 = ( 2 X ; 1,088 X ; 0 ) ,

P 6 = ( - 2 X ; 1,088 X ; 0 ) , P 7 = ( - 4 X ; - 1,425 X ; 0 ) .

Возбуждение u на экранах S ₁ – S ₄ задается плоской электромагнитной волной E ⁰ = ( 1; 0; 0 ) . Пятая тестовая задача заключается в определении u на параболическом бесконечно тонком идеально проводящем экране S 5 с фокусом 4 X и прямоугольным раскрывом Q 5 размера 10 Xx 10 X , расположенным в плоскости x 3 = 0. Возбуждение тока u на S 5 выполняется двумя точечными источниками, размещенными вблизи центров ( 0,75 X ; 0; 4 X ) , ( - 0,75 X ; 0; 4 X ) плоских бесконечно тонких идеально проводящих поверхностей q5 , Q 2 . Области Q 5 , Q ^ ориентируются в противоположную сторону оси x ₃ и задаются правильными пятиугольниками с радиусом описанной окружности 0,5 X .

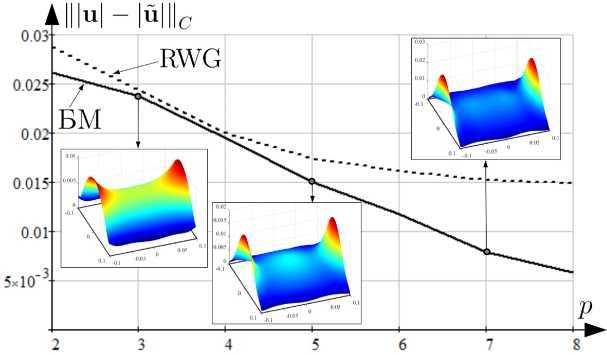
Рис. 6. Зависимость Щи| - |й||| от p для S 1 при расчете u БМ и RWG

Fig. 6. Dependence of Щй| - |u||| on p for S 1 when calculating u BM and RWG

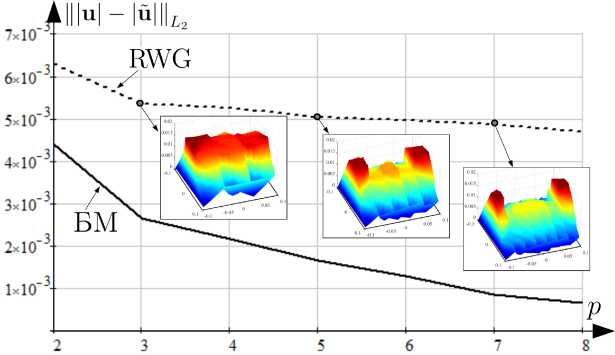
от p для S1 при расчете u БМ и RWG on p for S1 when calculating u BM and RWG

L 2

u

Рис. 7. Зависимость |||u| -|i

Fig. 7. Dependence of |||u| - |u||

Апостериорная оценка сходимости БМ проведена при изменении p. При этом число базисных функций RWG для соизмеримости с БМ вычислительных затрат для фиксированного p и Q выбиралось равным |мp . Также для заданных тесто- вых задач сходимость оценивалась относительно модуля плотности тока u = ^u1 u + u2u2 + u3u3

по нормам в С и L ₂ : |||u|-|й|||^ = max| |u|-|й|| и

III u|-I u|||

L 2

Iu| - |uI) d x соответственно.

Вычислительные алгоритмы для БМ и метода RWG реализованы в Microsoft Visual Studio C++ с использованием библиотек boost и armadillo с применением dll BLAS и LAPACK. Расчетная сетка для формирования базисных функций RWG для тестовых задач задавалась с использованием FreeFem++. Эталонные распределения плотности тока для указанных тестовых задач рассчита- ны на вычислительном сервере (Intel(R) Xeon(R) E5-2640V4 Broadwell-EP, DIMM DDR4 64 Гб) с применением САПР Ansoft HFSS для следующих установок (driven solution setupe): maximum number of passes = 50; maximum delta S = 10-8; lambda target = = 0,05; order of basis functions = second order.

На рис. 6, 7 представлены зависимости |||u| - |йЩ, |||u| - |й|||^ от p для первой тестовой задачи при вычислении БМ и методом RWG с отображением распределений |u| на S 1 для выборочных значений p .

На рис. 8, 9 представлены зависимости |||u| - |й|||, |||u| - |й||| от p для второй тестовой задачи при вычислении БМ и методом RWG с отображением распределений |u| на S 2 для выборочных значений p .

На рис. 10, 11 представлены зависимости |||u| - |й||| ^, |||u| - |й|||^ от p для третьей тестовой за-

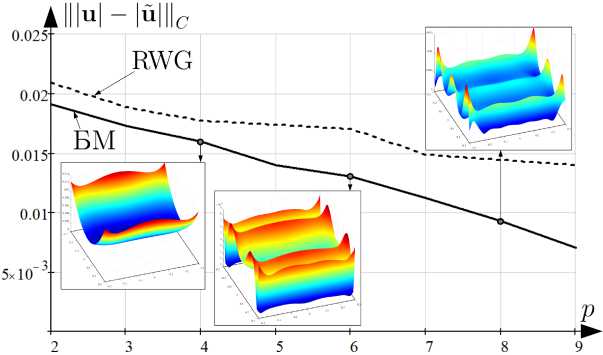
Рис. 8. Зависимость Щи| - |й||| от p для S 2 при расчете u БМ и RWG

Fig. 8. Dependence of Щи| - |u||| on p for S 2 when calculating u BM and RWG

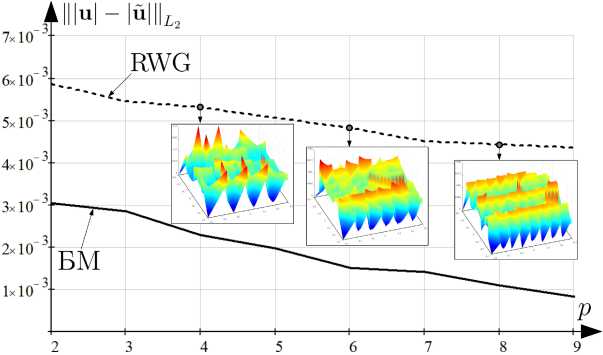
Рис. 9. Зависимость ||u| - |й||^

Fig. 9. Dependence of Щи| - |u|||^

от p для S2 при расчете u БМ и RWG on p for S2 when calculating u BM and RWG

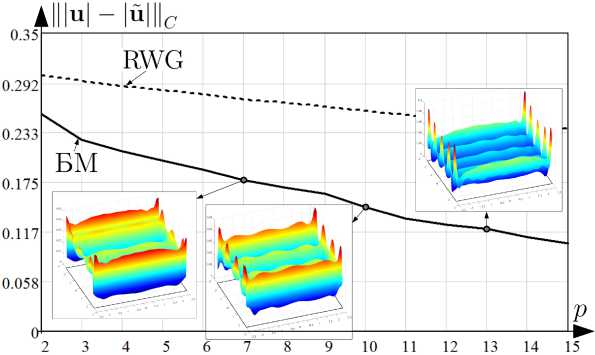
Рис. 10. Зависимость

Fig. 10. Dependence of

u| - |й|||_с от p для S 3 при расчете и БМ и RWG

II ^ul^- l^ul I L ^on p for S ₃ when calculating u BM and RWG

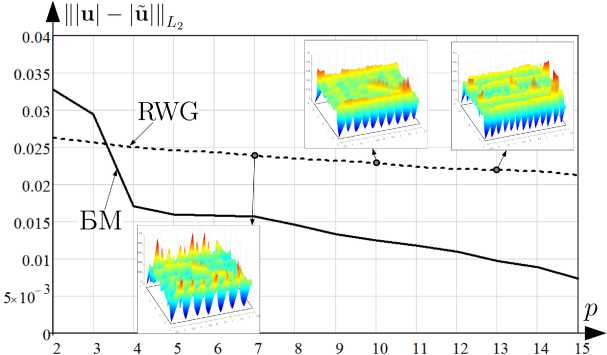
Рис. 11. Зависимость Щи| - |й|||

Fig. 11. Dependence of Щи| - |u||| от p для

L 2

_{L 2} on p for

S ₃

S ₃

при расчете u БМ и RWG when calculating u BM and RWG

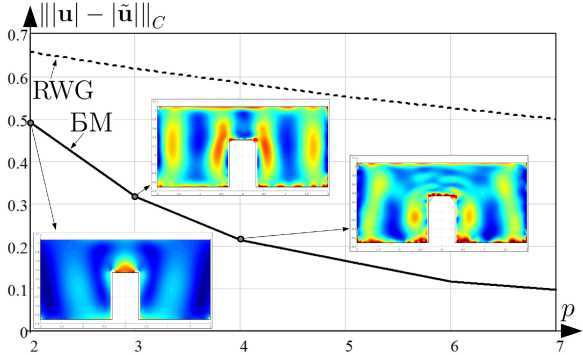
Рис. 12. Зависимость Щи| - |й||| от p для S 4 при расчете u БМ и RWG

Fig. 12. Dependence of Щи| - |u|||_c on p for S 4 when calculating u BM and RWG

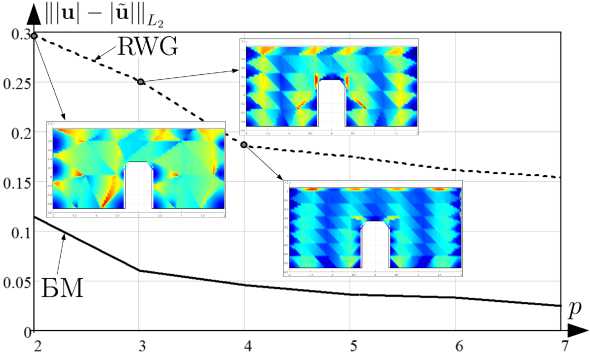
Рис. 13. Зависимость ||u| - |й|||^ от p для S 4 при расчете и БМ и RWG

Fig. 13. Dependence of ||u| - |u|||^ on p for S 4 when calculating u BM and RWG

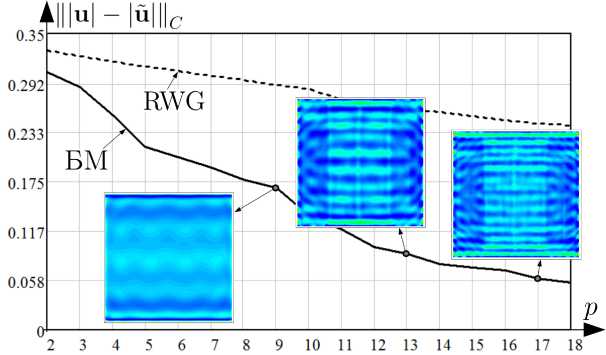
Рис. 14. Зависимость Щи| - |й||| от p для S 5 при расчете u БМ и RWG

Fig. 14. Dependence of Щи| - |u||| on p for 3 5 when calculating u BM and RWG

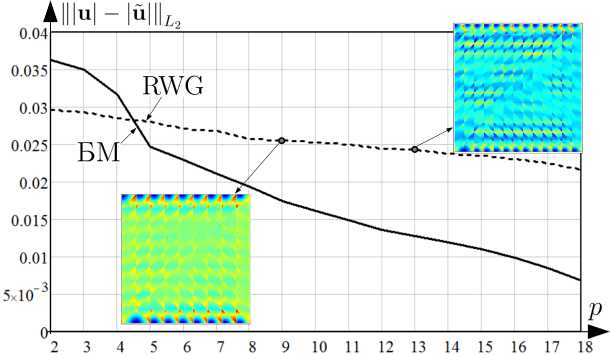
от p для S6 при расчете u БМ и RWG on p for S6 when calculating u BM and RWG

Рис. 15. Зависимость |||u| - |и|||

L 2

Fig. 15. Dependence of Щи| - |и|||

дачи при вычислении БМ и методом RWG с отображением распределений |и| на S 3 для выборочных значений p .

На рис. 12, 13 представлены зависимости |||и| - |й|Ц, Щи| - |й||| от p для четвертой тестовой задачи при вычислении БМ и методом RWG с отображением распределений |и| на S 4 для выборочных значений p .

На рис. 14, 15 представлены зависимости |||и| - |й|Ц, Щи| - |й||| от p для четвертой тестовой задачи при вычислении БМ и методом RWG с отображением распределений |и| на S ₅ для выборочных значений p .

Заключение

В целом результаты проведенного моделирования подтверждают более высокую эффективность барицентрического метода в решении задач электродинамического анализа ЗА в сравнении с методом RWG. Основное достоинство предлагаемой вычислительной схемы состоит в получении гладкой функции и на поверхности анализируемого экрана, которая при соизмеримом с методом RWG порядке аппроксимации позволяет получать более точное приближение и. Отдельно следует подчеркнуть полиномиальную скорость сходимости БМ, которая обеспечивает более существенный рост порядка точность с увеличением p в сравнении со сходимостью аппроксимации RWG. Сравнительные графические зависимости сходимости БМ (рис. 6–15) определяют, что выбор порядка аппроксимации p относительно анализируемой поверхности должен учитывать отношение в длинах волн геометрического размера Ω и степени кривизны S к |мp |. Получение соответствующих уточненных аналитических оценок с учетом результатов [13] относится к направле- ниям дальнейшего развития БМ в решении задач дифракции на проводящих тонких экранах. Также вычислительные результаты раскрывав простой (рис. 6–11) и сложной (рис. 12, 13) геометрических форм экранов во взаимосвязи с результатами [13] определяют одно из ключевых направлений развития БМ - решение задачи формирования оптимальной аппроксимации липшицевой функции на произвольном многоугольнике в барицентрическом представлении. Указанная задача также относится к направлениям дальнейших исследований. Ее разрешение предполагается при обобщении известных результатов по интерполяции липшицевой функции на отрезке, определяемых при переходе от многочленов Бернштейна или Лагранжа к многочленам Чебышева.