Электродинамика планарных отражающих структур с киральными слоями на основе тонкопроволочных спиральных элементов

В настоящее время несомненный интерес в СВч- и оптическом диапазонах представляет исследование, так называемых, метаматериалов, то есть структур, обладающих нетипичными для естественных сред электромагнитными свойствами. Одними из весьма интересных с точки зрения использования метаматериалов являются киральные среды, которые представляют собой композиционные структуры, состоящие из однородного контейнера и размещенных в нем проводящих элементов зеркально асимметричной формы. Начиная с 90-х гг. XX века имеется громадное число научных публикаций, посвященных исследованию киральных сред и структур на их основе. Подробно исследованы такие киральные элементы как объемные и плоские спирали, S-элементы, гаммадионы, двойные разомкнутые кольца, элементы Тел-леджена и др. Значительный вклад в развитие теории киральных метаматериалов внесли С.А. Третьяков, С.Л. Просвирнин, И.В. Семчен- ко, A.H. Sihvola, А.Д. Шатров, В.В. Шевченко, I.V. Lindell, Б.З. Каценеленбаум, A.J. Viitanen, A. Lakhtakia и многие другие [1–11]. Основными применениями киральных сред являются создаваемые на их основе частотно и поляризационно-селективные устройства СВч, преобразователи поляризации, малоотражающие покрытия, среды с отрицательным преломлением и др.

Интересными с точки зрения использования в качестве киральных элементов являются тонкопроволочные элементы в виде разомкнутых колец с выступающими концами (элемент Телледжена), многовитковые спирали, которые представляют собой некоторую суперпозицию электрических и магнитных диполей. Известны результаты исследования дифракции плоских электромагнитных волн на элементах Телледже-на (С.А. Третьяков, F. Mariotte) [12], цилиндрах с винтовой спиральной проводимостью (Б.З. Ка-ценеленбаум, А.Д. Шатров и др.) [8], где показано, что в структурах в виде длинных спиралей

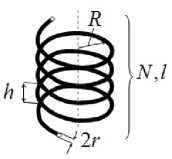
Рис. 1

малого по сравнению с длиной волны радиуса и решеток на их основе наблюдаются поляриза-ционно селективные резонансные явления. В ки-ральных средах на основе таких элемент выявлены частотно и поляризационно селективные свойства взаимодействия с электромагнитным излучением. В большинстве случаев для анализа электромагнитных свойств спиральных элементов используется теория электрических цепей и существует небольшое число работ, в которых предлагаются строгие электродинамические методы. Одной из проблем является построение дисперсионной модели кирального элемента и метасреды на основе совокупности таких элементов.

В предлагаемой работе в качестве объекта исследования выбран киральный метаматериал (КМ) на основе тонкопроволочных многовитковых спиралей, размещенных в однородном диэлектрическом контейнере. Интерес представляло построение математической модели спирального элемента, исходя из его электрических характеристик (индуктивности и емкости), а также модели самого метаматериала на основе матрицы из спиральных элементов. В результате построения такой модели получены частотные зависимости эффективной диэлектрической проницаемости и параметра киральности. Другим интересным аспектом является исследование многослойных и периодически неоднородных киральных метаструктур на основе спиральных элементов с использованием новой дисперсионной модели. С практической точки зрения, получены результаты, касающиеся возможности применения кирального метаматериала для частотно селективного перенаправления потока падающей СВч-энергии путем его преобразования в переизлучение в плоскости метаструктуры на определенных частотах [13; 14].

В работах [15; 16] построена математическая модель тонкопроволочного идеально проводящего спирального элемента и метаматериала на основе совокупности таких элементов, учитывающая дисперсию материальных параметров и взаимодействие между соседними элементами.

На основе теории цепей были рассчитаны через индуктивность и емкость резонансные частоты тонкопроволочного многовиткового кирального элемента. В отличие от других работ, при расчете емкости были рассчитаны поправки, связанные с межвитковой емкостью спирали, а также учтено взаимодействие спирали с соседними элементами путем вычисления межэлементной емкости. Использование подобной низкочастотной модели элемента позволило учесть произ- вольное число витков спирального элемента и также его электромагнитное взаимодействие с окружающими спиралями, что является крайне важным в силу наличия пространственной дисперсии киральной среды. Также в отличие от большинства других моделей, проволока не считается бесконечно тонкой. Геометрия спирального элемента приведена на рис. 1. На рис. 1 введены следующие обозначения: N – число витков; R – радиус витка; h – шаг спирали; l – длина спирали в развернутом состоянии и r – радиус тонкой проволоки.

После вычисления резонансной частоты спи- рального элемента too метаматериал описывался формулой Максвелла – Гарнетта с учетом дисперсии [11; 17]:

Б - Б„

— = с Б + 2 б ₈

^Б д ^(to) = ^Б г

x ( to ) = A-

Бг - Бд Бг + 2б5 ’

22 ;

too — to eOto (too — to2)

где Б _г — относительная диэлектрическая проницаемость контейнера; в о — параметр, имеющий размерность частоты и связанный с внутренними процессами в среде; с – скорость света; A – параметр, имеющий размерность длины; а — объемная концентрация микроэлементов в контейнере.

При подстановке в (1) явного выражения для резонансной частоты to o , получаются выражения для диэлектрической проницаемости и параметра киральности кирального метаматериала на основе тонкопроволочных спиральных элементов с учетом дисперсии в рамках предлагаемой модели. В дальнейшем расчеты показали, что использование предлагаемой низкочастотной модели ограничено по частоте и частотный предел использования определяется соотношениями между линейными размерами спиральных

элементов и длиной волны падающего СВч-излучения.

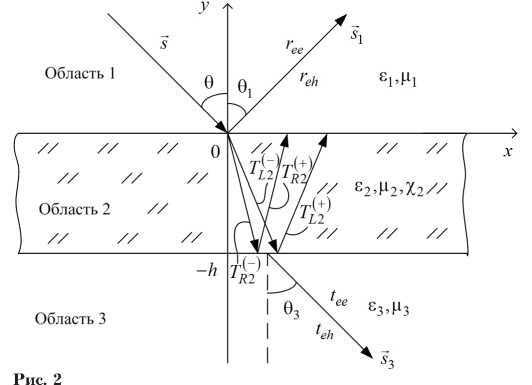
Далее было рассмотрено решение задачи об отражении плоской электромагнитной волны (ПЭМВ) линейной поляризации от планарного слоя кирального метаматериала на основе совокупности тонкопроволочных спиральных элементов в рамках предложенной дисперсионной модели. Геометрия задачи приведена на рис. 2. Область 2 на рис. 2 представляет собой планарный слой кирального метаматериала с параметрами £ 2 ( го ) , Ц 2 и Х 2 ( to ) ; области 1 и 3 — диэлектрические среды. На слой КМ падает ПЭМВ с перпендикулярной поляризацией под углом 6 . В результате решения электродинамической задачи требуется определить коэффициенты отражения ( r _ee, r _eh) и прохождения ( t _ee, t _eh) основных и кросс-поляризованных компонент поля. Здесь уместно отметить, что при взаимодействии электромагнитного поля (ЭМП) с киральными средами, всегда возникает кросс-поляризации, то есть переизлучение поля с составляющими векторов E , H , которые отсутствует в структуре ЭМП падающей волны.

Для описания кирального метаматериала были использованы материальные уравнения, согласно формализму Линделла – Сиволы [1]:

D = е(ю) E - i X(to) H,

— — — (2) B = цH + i x(to)E, где £ (to), ц, X (to) — относительные диэлектрическая, магнитная проницаемости и параметр ки-ральности метаматериала с учетом дисперсии. Материальные уравнения (2) записаны в Гауссовой системе единиц для правых форм кираль-ных элементов для гармонической зависимости векторов поля от времени.

Решение задачи осуществлялось методом частичных областей. На первом этапе уравнения Максвелла в дифференциальной форме для ЭМП в киральном метаматериале были сведены известным методом замены к уравнениям Гельмгольца относительно, так называемых, полей Бельтрами:

v ²E R + k R E R = 0; v ²E L + k L E L = о,         (3)

где E r l — векторы напряженности электрического поля волн с право и левокруговыми поляризациями в киральной среде (поля Бельтрами); k _R,L – волновые числа волн ПКП и ЛКП, определяемые как

kR,L = k0 (е12 (to) Ц12 ± X (to)),                     (4)

где k ₀ – волновое число для плоской электромагнитной волны в вакууме.

Решение уравнений (3) определяет ЭМП в слое кирального метаматериала:

E = E r + E l, H = i ^| ( E r - E l ) .           (5)

Электромагнитное поле в киральном слое 2 будет представлять собой суперпозицию 4-х волн: 2 волны, преломленные в слой из области 1 с ПКП и ЛКП и 2 волны, отраженные от области 3 с ПКП и ЛКП.

На следующем этапе решения задачи из уравнений Максвелла определяются векторы ЭМП в областях 1 и 2, а затем используются граничные условия для тангенциальных компонент векторов E , H на двух границах раздела «Область 1 — КМ» и «КМ – область 3». При подстановке выражений для составляющих векторов E , H в областях 1, 2, 3 в граничные условия:

EТ1) (у = 0) = EТ2) (у = 0);

HТ1) (у = 0) = HТ2) (у = 0);

• -^           -                             ⁽⁶⁾

E?) (у = -h) = eT3) (у = -h);

H Т2) (у = -h) = HТ3) (у = -h), получаем неоднородную систему из 8-и линейных алгебраических уравнений относительно неизвестных коэффициентов отражения и прохождения:

• -и- —— ——

AT = P ,                                      (7)

где A — квадратная матрица размером 8 х 8, явный вид элементов которой в автореферате не приводится в силу их громоздкости;

Рис. 3

*

T =

= [ r ee r eh T R ' T ^- T + <) t ee t eh ] ;

P =

= [ 0 - i J&C cos б/^/ц Т 00000 ] .

Коэффициенты матрицы A определяются геометрическими параметрами контейнера и спиральных элементов; материальными параметрами кирального слоя и областей 1 и 3, а также учитывают дисперсию S 2 ( to ) и Х 2 ( и ) и, как следствие, форму включений.

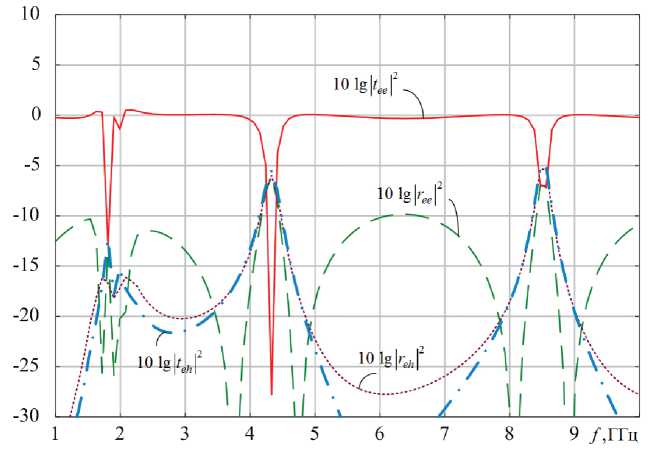
На рис. 3 представлены частотные зависимости отраженной и прошедшей мощностей основной и кросс-поляризованной компонент поля в диапазоне от 1 до 10 ГГц. Сплошными кривыми на рис. 3 показаны зависимости прошедшей мощности основной компоненты (10 lg t _ee ² ); штриховыми линиями – отраженной мощности основной компоненты (10 lg r _ee ² ); штрихпун-ктирными линиями – прошедшей мощности кросс-поляризованной компоненты (10 lg t _eh ² ); точечными линиями – отраженной мощности кросс-поляризованной компоненты (10 lg r _eh ² ). Падение волны на метаструктуру считалось нормальным. Расчет был выполнен при следующих значениях параметров структуры: R = 0.01 м, N = 3, r = 0.002 м, H = 0.05 м, d = 0.05 м.

На частоте 1.88 ГГц наблюдается условия для наилучшей концентрации энергии падающего излучения, так как уровни прошедшей мощности основной и кросс-поляризованной компонент поля имеют близко расположенные по частоте локальные минимумы (уровни ослабления прошедших мощностей основного и кросс- поляризованного поля более 20 дБ). Из рис. 3 видно, что вблизи частоты 1.88 ГГц на характеристике наблюдаются резонансные минимумы коэффициентов прохождения и отражения основной компоненты. В этом случае нормально падающий потоком энергии ЭМП преобразуется в ток энергии в плоскости метаматериала. На других частотах метаструктура является полностью прозрачной и падающее излучение через нее проходит практически без ослабления (вблизи 0 дБ). Таким образом, можно трактовать рассматриваемую структуру как частотно селективный концентратор СВч-энергии в районе частоты 1.88 ГГц. Также заметим, что исследуемая метаструктура по свойствам является эквивалентной естественному кристаллу (или искусственной брэгговской решетке) в оптическом диапазоне, а именно частоты резонансных минимумов ослабления прошедшей мощности основной компоненты поля вычисляются из условия Вульфа – Брэгга. Таким образом, достигается возможность дискретно-многочастотной концентрации падающей СВч-энергии на ряде резонансных частот.

В работе [18] получены выражения для элементов тензора поверхностного импеданса ки-рального метаматериала на основе совокупности тонкопроволочных спиральных элементов. В качестве использования тензора поверхностного импеданса для КМ и доказательства их применимости получены известные формулы Френеля для киральной среды без учета дисперсии.

Тензор поверхностного импеданса для КМ имеет следующий вид:

(- i^' kz „           Б (to) kos(to) Z =        2, 4 ,                           (8) k0 nc (to) i x(to) I   kze(to) Б (to) > где n2 (to) = б (to) Ц - Х2 (to); kz — продольная со*

ставляющая волнового вектора k в киральном метаматериале.

Также с использованием приближенных граничных условий для тонкого кирального слоя из работ В.А. Неганова, О.В. Осипова [7; 19–20] получена матрица передачи КМ, бесконечно протяженного вдоль одной из координатных осей.

N

Z (to) = n Zi (to),                               (10)

i = 1

где N – число слоев метаматериала.

В качестве примера рассмотрено решение задачи об отражении плоской электромагнитной волны (ПЭМВ) линейной поляризации от планарного двухслойного кирально-диэлектриче-ского метаматериала на основе совокупности тонкопроволочных спиральных элементов в рамках дисперсионной модели, полученной в главе 1. Геометрия задачи приведена на рис. 4. Область 2 на рис. 4 представляет собой планарный

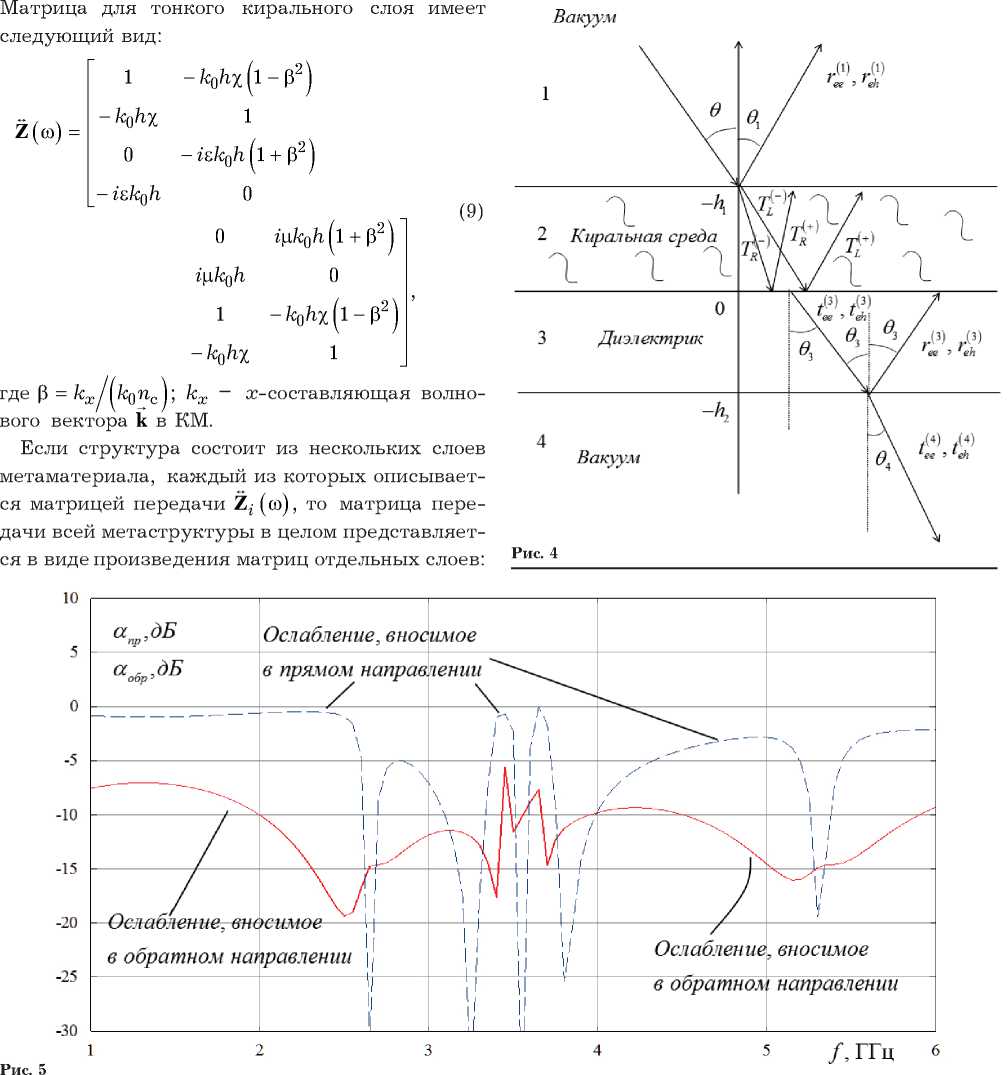
слой кирального метаматериала с параметрами Б 2 ( to ) , Ц 2 и Х 2 ( и ) ; область 3 — однородный слой диэлектрика; области 1 и 4 – диэлектрические среды. На двухслойную структуру падает ПЭМВ с перпендикулярной поляризацией под углом 9 . В результате решения электродинамической задачи требуется определить коэффициенты отражения ( r _ee, r _eh) и прохождения ( t _ee, t _eh) основных и кросс-поляризованных компонент поля.

Матрица передачи кирального слоя 2 определяется соотношением (8), в то время как матрица передачи диэлектрического слоя 3 получается из (9) при х = 0. Матрица передачи всей метаструктуры получается путем перемножения матриц двух слоев.

На последнем этапе решение задачи сводится к системе из 12-ти линейных алгебраических уравнений относительно неизвестных коэффициентов отражения и прохождения волн во внешних областях и внутренних слоях. Все коэффициенты обозначены на рис. 6. Индекс «e» относится к полю основной компоненты, индекс «h» – к полю кросс-поляризованной компоненты.

На рис. 5 представлены частотные зависимости отраженной и прошедшей мощностей основной компоненты поля в диапазоне от 1 до

• 6 ГГц. Штриховыми кривыми на рис. 7 показа-

• ны зависимости прошедшей мощности основной

= ioig | t ee ) |%

компоненты ( а пр

сплошными лини-

ями – отраженной мощности основной компо ненты (аобр = 10 lg pee) ). Падение волны на ме- таструктуру считалось нормальным для того, чтобы степень кросс-поляризации поля была незначительной. Диэлектрический слой обладает материальными параметрами б = 1.8, ц = 1 (пенополистирол) и толщиной 3 мм. Киральный слой выполнен на основе контейнера из пенополистирола толщиной 5 мм: б = 1.8 - i ■ 0.1, ц = 1. Кираль-ные спиральные элементы состоят из 2 витков радиусом 1 см и расположены на расстоянии 5 см друг от друга. Внешние области считались вакуумными. Как видно из рис. 5, на зависимостях наблюдаются узкие резонансные максимумы ослабления энергии в прямом направлении, на которых возможно эффективное преобразование нормально падающего СВч-излучения в боковое рассеяние в плоскости структуры. Из рис. 5 следует, что на частотах 2.7, 3.25, 3.6, 3.8 ГГц возможна ситуация, когда уровни ослабления в прямом направлении достигают –30дБ.

В заключение перечислим основные выводы из результатов проведенных исследований электромагнитных характеристик планарных киральных структур на основе тонкопроволочных идеально проводящих элементов спиральной формы:

• 1.    Предложена математическая модель на основе формулы Максвелла – Гарнетта и получены дисперсионные зависимости диэлектрической проницаемости и параметра киральности для кирального метаматериала на основе совокупности тонкопроволочных идеально проводящих элементов спиральной формы.

• 2.    Доказано, что в однослойном киральном метаматериале на основе тонко-проволочных многовитковых спиральных элементов возможно преобразование нормально падающего потока СВч-энергии на некоторых частотах в азимутальное рассеяние в плоскости метаматериала.

• 3.    В работе теоретически предсказана возможность дискретно-многочастотной концентрации падающей СВч-энергии при помощи однослойной киральной метаструктуры на ряде резонансных частот.

• 4.    Доказано, что двухслойный кирально-диэ-лектрический метаматериал на основе тонкопроволочных проводящих микроспиралей вблизи заранее заданной частоты позволяет выполнять частотно-селективное преобразование нормально падающего потока электромагнитной энергии в азимутальное рассеяние в плоскости метаструктуры.