Электроконвекция слабопроводящей жидкости при униполярной инжекции и нагреве сверху

В слабопроводящих жидкостях, помещенных в электрическое поле, благодаря различным механизмам образования в ней свободных или поляризационных зарядов, может возникать и поддерживаться электроконвекция [1–5]. Так, в случае инжекционного механизма свободный заряд появляется на границе жидкость–электрод вследствие окислительно-восстановительных электрохимических реакций [4, 6]

При этом в приграничных зонах генерируются заряды, совпадающие по знаку с зарядом электродов.

В данной статье рассматривается униполярная инжекция с катода. В этом случае находящиеся у электрода атомы нейтральной примеси захватывают электроны и становятся отрицательными ионами [7]:

M + ( X+ Y- ) ^ M ( e ) + ( XY_ ) ^ f,

вглубь жидкости. Далее, сила Кулона действует на распределенный в объеме заряд, и вследствие этого порождается электроконвективное течение.

В изотермической жидкости, находящейся в постоянном электрическом поле, в результате обратной бифуркации возникает стационарная электроконвекция [8, 9]. В некотором интервале изменения электрического числа Релея, зависящего от напряжения на электродах, имеется два устойчивых режима: ионная проводимость в неподвижной жидкости (conductive state) и электроконвективное течение; между ними существует гистерезисный переход.

Электроконвекция в неизотермической жидкости, благодаря взаимодействию кулоновских сил и сил плавучести, открывает дополнительные возможности. Слабопроводящие жидкости в электрическом поле демонстрируют разнообразие нелинейных электроконвективных структур, что представляет значительный интерес как с фундаментальной, так и с практической точек зрения. Здесь возможно усиление [10, 11] или ослабление [12] теплопередачи при нагреве снизу областей, заполненных жидкостью. В работах [10, 11] обнаружены только установившиеся стационарные режимы электроконвекции, однако следует отметить, что при численном моделировании на боковых границах горизонтальной электроконвективной ячейки рассматривались граничные условия Неймана для электрического потенциала, плотности заряда и температуры и непротекания по горизонтали, что заведомо исключало решения в виде бегущих волн. Хаотические колебательные течения обнаружены в [13] при нагреве замкнутой полости сбоку (сила плавучести и кулоновские силы ортогональны друг другу). Стационарная электроконвекция в широком зазоре между горизонтальными коаксиальными цилиндрами при изменении угола между радиальным электрическим полем и направлением силы тяжести изучалась в [14]. Показано, что с ростом электрического числа Релея T решение в виде конвективного факела меняется на решение в виде радиального движения с большим количеством конвективных ячеек, что значительно увеличивает теплоотдачу.

Исследование нелинейной стадии электроконвекции при нагреве сверху [7, 15, 16], проведенное в безындукционном приближении в случае, когда заряд на катоде пропорционален приложенному полю, продемонстрировало не только повышение порога для зарождения стационарной конвекции, но и возможность образования колебательной неустойчивости. В результате прямой бифуркации Хопфа рождаются волновые электроконвективные течения: стоячая волна (SW), бегущая волна (TW), модулированная бегущая волна (MTW), модулированная стоячая волна (MSW), которые могут быть реализованы в горизонтальном слое или кольцевых каналах. Такое поведение слабопроводящей жидкости связано с перераспределением заряженной примеси и в некотором смысле является аналогом конвекции бинарных смесей, в которых в результате эволюции колебательных возмущений могут возникать стационарные и волновые структуры, в том числе стоячие и бегущие волны, активно изучаемые на основе численного моделирования в [17–25].

Формирование электроконвективных структур — пример явления самоорганизации. Благодаря этому процессу электроконвекция нашла практическое применение как эффективный способ управления теплопередачей. Эксперименты [26] показывают, что число Нуссельта для теплопередачи в условиях электроконвекции может увеличиваться на порядок.

В данной работе для заполненного слабопроводящей жидкостью и нагреваемого сверху горизонтального конденсатора при численном моделировании используются периодические граничные условия, дающие возможность существования бегущих волн. Предполагается, что инжекция заряда с катода постоянна и однородна. Задача решается в полной постановке (без безындукционного приближения). Проанализированы двумерные режимы электроконвекции. Исследовано влияние внешнего электрического поля на эволюцию в межэлектродном промежутке таких электроконвективных колебательных течений, как бегущие волны, модулированные бегущие волны, смешанный режим, содержащий фазы стоячей и бегущей волн. Получена бифуркационная диаграмма решений и распределения гидродинамических и электрических полей в конденсаторе.

2.    Постановка задачи

Рассматривается плоский бесконечный горизонтальный конденсатор толщиной d , заполненный вязкой несжимаемой слабопроводящей жидкостью и расположенный в поле силы тяжести g (далее для краткости — физическая система). Ось x направлена по верхней обкладке конденсатора, ось z — перпендикулярно ей, в слой жидкости, ось у — по нормали к плоскости { x, z } (Рис. 1). На обкладки конденсатора подается постоянная разность потенциалов V , также между ними присутствует постоянная разность температур 0 ; жидкость нагревается сверху. На верхней обкладке конденсатора, являющейся катодом, генерируется постоянный отрицательный заряд (осуществляется автономная униполярная инжекция, Ε — напряженность электрического поля).

е<о)=0, ф<о)=о

А © © © © © © © © © © >х

V

е(^, ФИ=г0

Рис. 1 . Геометрия задачи и граничные условия

Жидкость обладает следующими постоянными параметрами:    динамической    вязкостью     п, температуропроводностью %, подвижностью зарядов K    и диэлектрической проницаемостью -.

Предполагается, что плотность жидкости ρ линейно зависит от 0 — отклонения температуры от средних значений:   р = р₀ ( 1 -в_т0 ) , где р₀   — плотность

1 жидкости при средней температуре, в_т =-- ρ ₀

д р j д T J

коэффициент объемного расширения жидкости.

_                                                                г                                    d 2 Ро

Для обезразмеривания задачи используем следующие масштабы: длины — d , времени —

п пп скорости--, температуры — 0, давления--- , электрического потенциала Ф — Vo, плотности

Ро d                                          Ро d 2

заряда q

^- 0^-' 0

d2  ,

где    - ₀

диэлектрическая постоянная. Тогда система безразмерных

гидродинамических уравнений, описывающих электроконвекцию, примет вид:

• — + ( v V ) v = -V p + A v - T- q VO - Ra 0 e ,

д t                      M2        Pr q++(vV) q=MF (q 1 -™-V q)•

• —+ ( v V ) 0 = — A0 , д t   ^{V !} Pr

div v = 0,

АФ=- q .

Она состоит, соответственно, из уравнения Навье–Стокса, записанного в приближении Буссинеска (неоднородность плотности учитывается лишь в массовых силах), закона сохранения заряда, уравнения теплопроводности, условия несжимаемости жидкости, уравнения Пуассона, связывающего электрический потенциал с плотностью заряда [7, 27].

На идеально проводящих горизонтальных границах (на обкладках) выполняются условия прилипания жидкости:

z = 0:   v = 0, 0 = 1,  Ф = 0, q = C,

z = 1:   v = 0, 0 = 0, Ф = 1.

На катоде происходит автономная униполярная инжекция, что соответствует однородной и постоянной плотности заряда при z = 0.

Система уравнений (2) и граничные условия (3) содержат следующие обозначения: t — время; v — скорость жидкости; p — давление; e — единичный вектор, сонаправленный с осью z Кроме этого,

Ро g P ^{d 30}

используются безразмерные параметры: число Релея Ra = —0-----; электрическое число Релея пх

(электроконвективный параметр) T = -⁰—⁰ ; число Прандтля Pr =--- ; параметр подвижности ионов

K п                      Р 0 Х

-о-                                  q^d²

M =   0— ; параметр инжекции C =---- , где q₀ — плотность заряда, инжектируемого на катоде.

V к ^Р 0                             V 0 - 0 -

Уравнение Навье–Стокса, входящее в систему (2), содержит слагаемые, отвечающие за силу Кулона, действующую на присутствующий в жидкости отрицательный заряд, и за силу Архимеда, выталкивающую вверх расширенную за счет нагрева жидкость. В такой постановке инжекционный механизм является основным механизмом возникновения конвекции: генерируемый отрицательный заряд отталкивается от катода и увлекает за собой жидкость, а термогравитационный механизм в данной конфигурации сам по себе конвективное движение вызвать не может. Однако взаимодействие сил Кулона и Архимеда приводит к осцилляциям и волновым течениям (горячая жидкость на катоде, увлеченная силой Кулона вниз, стремится вернуться обратно под действием силы Архимеда).

3.    Метод решения задачи

В силу отсутствия анизотропии в горизонтальной плоскости можно рассмотреть случай двумерных возмущений:  v = (vx, 0, vz). Такой подход позволяет применить двухполевой метод, исключающий из уравнения Навье-Стокса давление. Согласно методу, вводим связанные со скоростью сплошной среды функцию тока w и вихрь скорости ю:

5w       5w      z х

vr =--, vz = —, ю = (rotv) .

x     5 z         5 x        ^v     y^y

После подстановки выражений (4) в систему (2) и математических преобразований получаем систему относительно функции тока и вихря скорости:

<

5ю дю 5w 5ю 5w .    T ²

----- +--- = Аю + —-

M ²

5 t   5 x 5 z   5 z 5 x

5 q 5 q 5w 5 q dw Ht "a x sT 5 z a x

5 Ф 5 q 5 Ф 5 q — 5 z 5 x 5 x 5 z

= M ( q ²"х q ) •

59  56 5w  56 5w 1 _

----- +--- = — A6 , 5 1  5 x 5 z  5 z 5 x   Pr

А Ф = — q ,

Aw = —ю ,

—

Ra 59

Pr 5 x ’

с соответствующими граничными условиями:

z = 0: w = 0,  — = 0,   6 = 1, Ф = 0, q = C ,

5 z

z = 1: w = 0, — = 0,   6 = 0, Ф = 1.

5 z

Кроме того, из-за горизонтальной бесконечности слоя на физическую систему накладываем периодические граничные условия с периодом l = 2 (такому периоду отвечает волновое число к = 2л/ l = п , равное критическому волновому числу возникновения термогравитационной конвекции при нагреве жидкости снизу в отсутствие электрических взаимодействий):

F ( x , z , t ) = F ( x + l , z , t ) , (7)

где F — любая из функций системы уравнений (5).

Систему (5) с граничными условиями (6), (7) решаем численно, методом конечных разностей [9, 28]. При аппроксимации уравнения Навье-Стокса (5)₁, закона сохранения заряда (5)₂ и уравнения теплопроводности (5)₃ применяем явную схему по времени. Реализуем «переключение» между схемами против потока и схемами центральных разностей в зависимости от величины локального критерия устойчивости. Уравнения Пуассона (5) 4 и (5) 5 решаем методом последовательной верхней релаксации на каждом временном шаге. Для численного моделирования накладываем на расчетную область сетку с числом узлов 21x41. Причина выбора именно такого ее размера обсуждается в последнем разделе данной статьи.

При анализе решений рассматриваем как локальные, так и интегральные характеристики физической системы. Основной исследуемой функцией является функция тока w ; в каждый момент времени в ячейке сетки оцениваем ее максимальное и минимальное значения: Vn_BX ( t ) = max[v,₇ ( Ч ) ] , Vmin ( t ) = min [w,_v ( t_k ) ], и значение в фиксированной точке wi_oc ( t ) = w ( 0,5; 0,5; t_k ) . Также определяем Фурье-спектр колебаний функции тока в фиксированной точке ячейки wi_oc и зависимости от времени амплитуд разложения функции тока w ( x ; 0,5; t_k ) в ряд Фурье по горизонтальной координате x .

Волновые решения характеризуются фазовой скоростью жидкости, которая находится как производная по времени горизонтальной координаты, отвечающей максимуму функции тока в ячейке:

dx vph

( V=V max )

dt

Пространственно-временное разложение полей функции тока в ряды Фурье по пространственным гармоникам F_n ( t ) (например, в горизонтальном направлении в сечении, соответствующем середине высоты слоя z = 1/2):

f I ^ , z = -, t | = F ( t ) + Z ¹⁷ n ( t ) e ’ V        ²  )             n = 1

позволяет охарактеризовать особенности различных течений жидкости. Для описания возникающих в жидкости структур в обсуждаемом случае достаточно знать информацию о первой V ( t ) и второй модах у₂ ( t ) разложения функции тока, вклад третьей гармоники ф₃ ( t ) в общее решение мал (не превышает 1%).

4.    Результаты исследования

Для численного моделирования физической системы использовались следующие значения безразмерных параметров: число Релея Ra =— 2500; число Прандтля Pr = 10 ; параметр подвижности ионов M , способный принимать широкий набор значений 4 <  M <  120, взят равным 14,14 (это наиболее часто употребляемое значение [7, 9, 14, 15, 29]). Параметр C=- 0,224 соответствует умеренной униполярной инжекции (0,2 <  C <  5) [30]. Примерами жидкостей, свойствам которых близок приведенный набор параметров, могут служить этанол с ионами хлора [8] или циклогексан с добавлением соли триизоамиламмония перхлората и тетраметилфенилендиамина, заполняющий конденсатор с электродами из нержавеющей стали [29]. В работе [29] при изучении униполярной однородной инжекции диапазон зазоров между электродами составлял 0,1–1,5 мм, напряженность электрического поля изменялась в пределах 0–100 кВ/см. Для оценок в дальнейшем расстояние между электродами выбиралось равным 1,5 мм и напряжение между электродами 4,2 кВ ( E = 28 кВ/см).

Исследование проводилось следующим образом: при фиксированном наборе безразмерных параметров, приведенном выше, задавалось начальное возмущение в виде двух противоположно вращающихся конвективных валов с малой амплитудой. При этом электрическое число Релея T , пропорциональное напряжению на обкладках конденсатора и являющееся в данном случае управляющим параметром, постепенно увеличивалось до тех пор, пока возмущения не начинали нарастать, а жидкость — двигаться. Далее применялся метод продолжения по параметру, позволяющий получить бифуркационную диаграмму электроконвективных течений.

Задача определения функций системы (2) в отсутствие движения жидкости (в равновесном состоянии 5/5 1 = 0, v = 0) решена аналитически. Уравнение теплопроводности в этом случае сводится к тривиальному дифференциальному уравнению для отклонения температуры от среднего значения в виде линейной зависимости: 0₀ = 1 - z . Равновесные распределения заряда q₀ и потенциала Ф_о записываются так:

3 C ² ( 2 Cz + 1 ) '2 q 0 = —, _   , уз

1 - ( 2 с + 1 )

1 - ( 2 Cz + 1 ) 3 2

1 -(2 C +1)32 ’ где параметр C связан с величиной инжектируемого заряда, С = 3C2/(1 -(2C +1)/ ). Таким образом, для каждого рассматриваемого значения C можно численно находить значение коэффициента C .

К примеру, используемому в данной работе значению С =- 0,224 соответствует C = 0,25 .

• 4.1.    Смешанный режим M

  

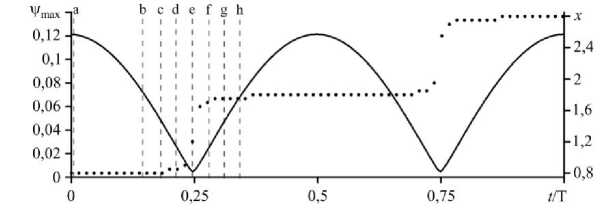
  Рис. 2. Зависимости от времени максимального значения функции тока в ячейке (сплошная линия) и его x -координаты (пунктирная линия) в смешанном режиме M; T = 6815 ; буквами a, b, .„, h обозначены характерные моменты времени, в которые получены распределения функции тока

  
  

  При последовательном увеличении электрического числа Релея T от значений для области неподвижной жидкости (малые колебания затухают) до T = T_C1 = 6805 благодаря прямой бифуркации Хопфа возникает конвекция в виде смешанного режима M (Mixed).

Данный режим назван так вследствие того, что является комбинацией режима стоячих волн и режима бегущих волн, которые периодически сменяют друг друга. Большую часть периода колебаний жидкость существует в форме стоячих волн. В момент максимума интенсивности конвекции в ячейке присутствуют два симметричных конвективных вала, закрученных в противоположные стороны (момент времени a на Рис. 2 и отвечающее ему распределение на Рис. 3). Центр конвективного вала, вращающегося против часовой стрелки, имеет горизонтальную координату x = 0,85, центр вращающегося по часовой стрелке вала — x = 1,85. Затем интенсивность конвекции в валах начинает уменьшаться (см. моменты времени c–e на Рис. 2 и соответствующие распределения на Рис. 3) и достигает некоторого малого значения (утах = 0,005 при времени e Рис. 2). Это отличает смешанный режим от «чистых» стоячих волн, при которых интенсивность конвекции в ячейке упала бы до нуля, а затем валы просто поменялись местами. Кроме того, резкое увеличение координаты максимума функции тока со значения x = 0,85 в момент времени d до значения x = 1,85 в момент f на рисунке 2 и эволюция соответствующих распределений функции тока на рисунке 3 подтверждают, что в этой части смешанного режима проявляется бегущая волна. Вблизи малого значения интенсивности конвекции жидкость как единое целое продвигается в горизонтальном направлении, и именно таким образом валы сменяют друг друга. Еще одним признаком наличия бегущей волны служит искривление границ между областями положительных и отрицательных значений функции тока (см. моменты d–f на Рис. 3). В момент времени g закрученный против часовой стрелки конвективный вал располагается в правой части ячейки, а противоположный вал — в левой. Вновь наступает фаза стоячей волны. Интенсивность конвекции увеличивается до некоторого максимального значения при t/T = 0,5 . Легко представить эволюцию поля функции тока за полупериод 0,5 < t/T < 1, если на рисунке 3 мысленно поменять местами области ее положительных и отрицательных значений.

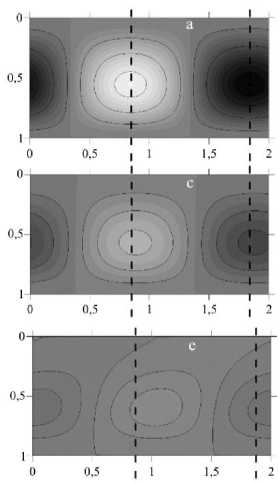
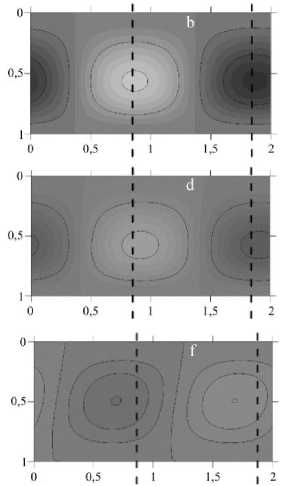
Рис. 3. Распределения функции тока в ячейке при смешанном режиме M при T = 6815 в моменты времени a-h, выделенные на рисунке 2; единая шкала изменения функции тока v

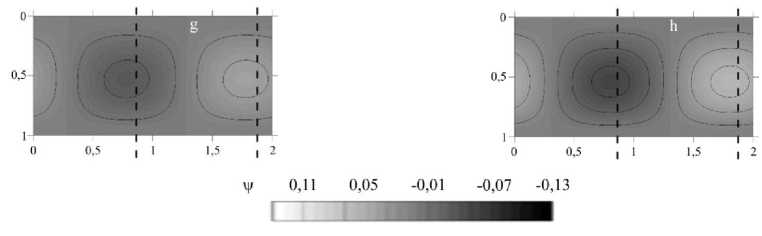
Рис. 3. Продолжение

Рис. 4. Распределения в ячейке отклонений от равновесных значений: температура ( а ), плотность заряда ( б ), электрический потенциал ( в ), в смешанном режиме M в момент времени а (см. Рис. 2); T = 6815; показаны изолинии функции тока (сплошная линия – положительные значения, штриховая – отрицательные)

Распределения прочих функций физической системы приведены на рисунке 4. Как можно видеть, заряд и потенциал в смешанном режиме при отсутствии движения жидкости отклоняются от своих значений крайне слабо.

При увеличении электрического числа Релея T максимальная амплитуда колебаний жидкости в ячейке растет, а при значении T =Т_с2 = 6818 в жидкости устанавливается режим бегущих волн TW.

• 4.2.    Режим бегущих волн TW

  Режим бегущих волн (TW — Traveling Wave) является основным режимом электроконвекции в надкритической области электрического числа Релея, и существует при Те [ Т_С2 = 6818, Т_сз = 7037 ] . В результате эволюции начального возмущения случайным образом может сформироваться волна, бегущая как вправо, так и влево, что соответствует симметрии задачи (5) относительно инверсии направления x . Поскольку в работе используется метод продолжения по параметру, то с ростом электрического числа Релея подробно исследовалась волна, бегущая влево.

В режиме бегущих волн в ячейке

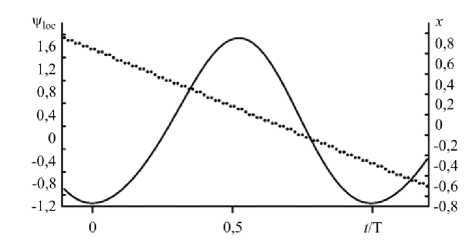
Рис. 5. Зависимость от времени значения функции тока в фиксированной точке ячейки у_1ос (сплошная линия) и x -координаты максимума функции тока в ячейке (пунктирная линия) в режиме TW; Т = 6950

одновременно существует два конвективных вала, вращающихся в противоположные стороны, и движущихся в горизонтальном направлении с постоянной фазовой скоростью, о чем свидетельствует линейный характер зависимости координаты максимума функции тока от времени (Рис. 5). Интенсивность конвекции в валах остается постоянной. Распределения некоторых функций в ячейке представлены на рисунке 6.

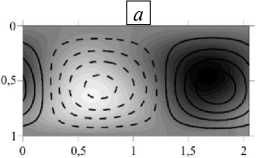
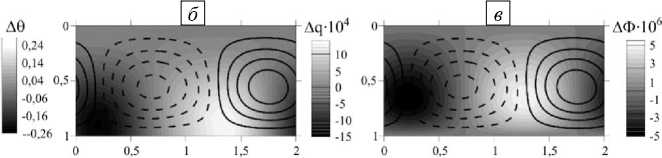
Рис. 6. Распределения отклонений от равновесных значений: температура ( а ), плотность заряда ( б ), электрический потенциал ( в ), в режиме бегущих волн TW в момент времени, соответствующий левой вертикальной оси рисунка 5; Т = 6950 ; показаны изолинии функции тока (сплошная линия – положительные значения, штриховая – отрицательные)

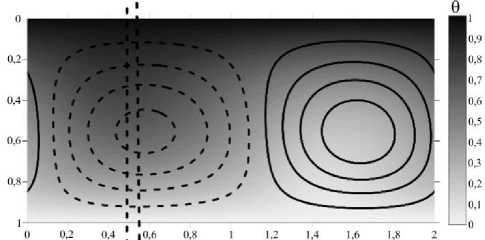
Для лучшего понимания пространственных распределений характеристик физической системы в режиме бегущей волны в определенный момент времени сделан разрез, проходящий по середине высоты ячейки, и найдены распределения функций, характеризующих течение (за исключением вихря скорости) (Рис. 7). Как можно видеть, отклонения параметров (температуры, заряда и потенциала) от равновесных значений в целом соответствуют распределению в пространстве конвективных валов. Отклонения заряда и потенциала почти максимальны и положительны вблизи координаты ( x = 1,15), где функция тока, увеличиваясь, проходит через ее нулевое значение. При этом жидкость под действием силы Кулона на избыточный положительный заряд движется вверх, к катоду. С другой стороны, отклонения заряда и потенциала отрицательны вблизи координаты ( x = 0,05), где сила Кулона и скорость жидкости направлены от катода. Стоит отметить, что потенциал возмущается крайне слабо. Экстремальные отклонения температуры от равновесия немного смещены относительно центров конвективных валов: например, в центре закрученного против часовой стрелки конвективного вала (штриховые линии) содержится более нагретая жидкость. Наблюдается некоторая асимметрия вращения соседних конвективных валов: распределение модуля скорости в ячейке имеет два экстремума, меньший из которых соответствует движению жидкости в направлении нагретого катода (когда сила Кулона и сила плавучести противоположны друг другу), а больший — движению жидкости в направлении от катода (когда силы плавучести и Кулона сонаправлены).

а

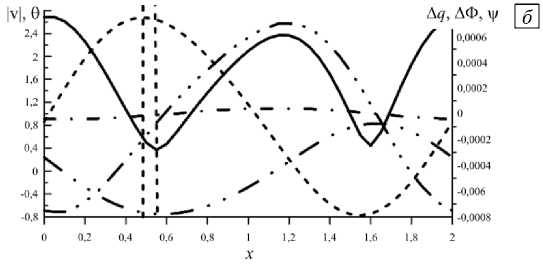
Рис. 7. Режим бегущих волн  (TW)

при T = 6950    в    момент времени, соответствующий левой вертикальной оси рисунка 5; (а) – распределение температуры в ячейке и изолинии функции тока v (сплошные линии – положительные значения, штриховые – отрицательные); (б) – графики функций, характеризующих течение в зависимости от горизонтальной координаты x, в сечении, расположенном на середине высоты ячейки: v – модуля скорости жидкости (сплошная линия), 0 - температуры (штриховая линия), отклонений от равновесных распределений заряда Дq (штрихпунктирная линия с тремя точками) и электрического      потенциала      ДФ

(штрихпунктирная линия), функции тока v (штрихпунктирная линия с двумя точками); зависимость    температуры    построена в условном масштабе (то есть абсолютные значения     отклонения     температуры не соотносятся с абсолютными значениями ни функции тока, ни электрических характеристик)

Экстремумы горизонтальных распределений различных функций в ячейке не совпадают друг с другом. Особенно это проявляется у температуры: максимум ее значения (координата x = 0,45 , левая вертикальная штриховая линия на Рис. 7) расположен левее центра конвективного вала, закрученного против часовой стрелки ( x = 0,55, правая вертикальная штриховая линия на Рис. 7). С учетом того, что жидкость в ячейке как единое целое движется справа налево, можно заключить: изменение температуры опережает по фазе изменение функции тока чуть больше чем на п, а возмущения заряда и потенциала опережают изменение функции тока приблизительно на п/2.

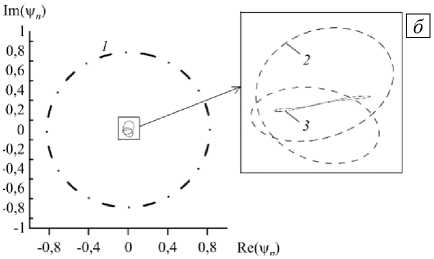
Коэффициенты трех гармоник разложения горизонтального распределения функции тока в ряд Фурье представлены в виде зависимостей от времени и фазовых траекторий (параметрическая зависимость между мнимой и действительной частями гармоник) на рисунке 8. Коэффициенты разложения функции тока в ряд Фурье, конечно, будут зависеть от времени, поскольку жидкость в конденсаторе вместе с конвективными валами движется в горизонтальном направлении. Однако по значениям максимумов гармонических коэффициентов можно заключить, что в режиме бегущих волн доминирует именно первая гармоника, ее максимальные значения более чем в 10 раз превышают значения второй гармоники. По фазовым траекториям же можно понять, что первая гармоника меняется со временем по гармоническому закону, а вот вторая и третья — по ангармоническому. Но именно их вклад в конечном итоге и приводит к появлению слабой, почти незаметной асимметрии в пространственном распределении конвективных валов.

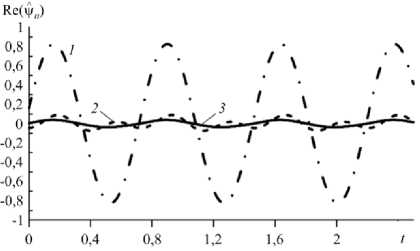
Рис. 8. Зависимость от времени коэффициентов первых трех гармоник разложения в ряд Фурье функции тока в горизонтальном разрезе ( а ) и фазовые траектории ( б ) в режиме бегущих волн, T = 6950

а

4.3. Режим модулированных бегущих волн MTW

При дальнейшем увеличении электрического числа Релея T

и превышении им значения Т_с3 = 7037

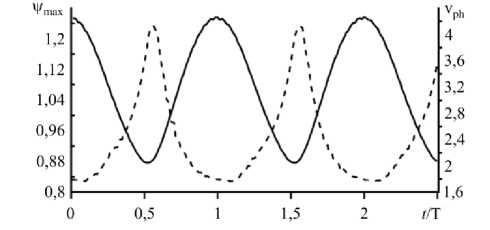
Рис. 9. Зависимость от времени значения функции тока в фиксированной точке ячейки ψ (сплошная линия) и фазовой скорости v максимума функции тока в ячейке (штриховая линия) в режиме MTW; T = 7050

в системе возникает режим модулированных бегущих волн (MTW — Modulated Traveling Wave). Он похож на режим бегущих волн (режим TW), так как в ячейке присутствуют два конвективных вала, закрученных в противоположные стороны и двигающихся в горизонтальном направлении. Но, в отличие от режима TW, в режиме MTW интенсивность конвекции в валах и скорость перемещения максимума и минимума функции тока в ячейке начинают зависеть от времени по некому периодическому закону. Как видно на рисунке 9, максимуму интенсивности конвекции в конвективном вале соответствует минимум его горизонтальной скорости, и наоборот. Кроме того, появляется асимметрия

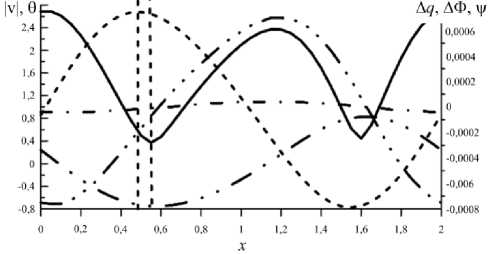
в конвективных валах: один из валов периодически расширяется и интенсивность конвекции в нем падает; второй, наоборот, сжимается и жидкость в нем начинает течь быстрее (Рис. 10 а ). После этого начинает расширяться второй вал, и так далее. Для режима MTW также получены графики функций системы в вертикальной плоскости { x, z } (Рис. 10 б ).

а

б

Рис. 10. Режим модулированных бегущих волн (MTW) в момент времени, соответствующий левой вертикальной оси рисунка 9, T = 7050 : (а) – распределение температуры в ячейке и изолинии функции тока v (сплошная линия -положительные значения, штриховая – отрицательные); (б)  – графики функций, характеризующих течение, в зависимости от горизонтальной координаты x, в сечении, расположенном на середине высоты ячейки: v – модуля скорости жидкости (сплошная линия), 6 - температуры (штриховая линия), отклонений от равновесных распределений заряда Дq (штрихпунктирная линия с тремя точками), электрического потенциала ДФ (штрихпунктирная линия) функции тока v (штрихпунктирная линия с двумя точками); зависимость температуры построена в условном масштабе

а

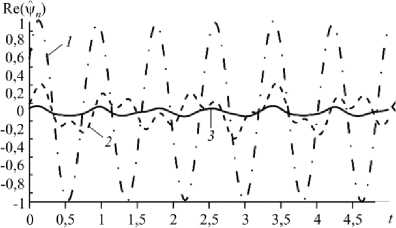
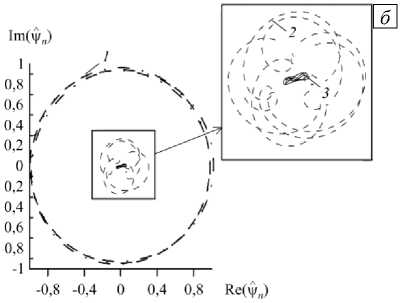
Рис. 11. Зависимость от времени коэффициентов трех первых гармоник разложения в ряд Фурье функции тока в горизонтальном разрезе ( а ) и фазовые траектории ( б ) в режиме модулированных бегущих волн, T = 7050

Хотя сдвиги фаз в пространственных распределениях функций качественно не меняются в сравнении с режимом TW, тем не менее асимметрия противоположно вращающихся валов становится заметной у всех функций, характеризующих решение в виде модулированной бегущей волны.

Коэффициенты при пространственных гармониках функции тока представлены на рисунке 11. Как видно из графиков, в режиме MTW большую роль начинает играть вторая гармоника, ее максимальное значение всего в три раза меньше максимального значения первой гармоники. Помимо всего прочего, амплитуда первой гармоники в этом случае начинает зависеть от времени. Судя по всему, появление сильной второй гармоники в колебаниях исследуемой физической системы и приводит к значительной асимметрии в пространственном распределении функций.

Для экспериментального наблюдения и изучения конвективных бегущих волн, например, в смесях спирт–вода, используются кольцевые каналы [20, 21]. Это важно, так как у конвекции в бинарной смеси и электроконвекции в жидкости существуют общие черты: 1) конвективный перенос примеси (заряда) конкурирует с другими механизмами переноса (термодиффузией нейтральной примеси по направлению градиента температуры или противоположно ему, дрейфом зарядов в электрическом поле); 2) конвекция может возникать колебательным образом, в результате эволюции формируется бегущая волна.

Геометрия кольцевых каналов трехмерна, но в каналах большого радиуса R >> d длиной L = 2 nR и шириной 1,3 d ^ 3 d [21] реализуются квазидвумерные режимы конвекции бинарной смеси в виде бегущих валов, оси которых перпендикулярны боковым границам. Полученные при численном моделировании бегущих волн в горизонтальном слое бифуркационные диаграммы решений и распределения примеси [21, 22] находятся в хорошем соответствии с экспериментальными результатами для кольцевых [21] и прямоугольных каналов [23]. При ширине канала, большей 3 d , квазидвумерные валы разрушаются из-за трехмерных неустойчивостей [24]. В узких каналах влияние боковых границ настолько велико [25], что результаты существенно расходятся с предсказанными численным расчетом.

Для экспериментальной проверки этих выводов из анализа двумерных структур рассмотрим волновое движение в кольцевом канале длиной L = ml >>1, где т — целое число (размерная длина L = 2 md >> d ). При небольших надкритичностях параметра T подбором L можно добиться, чтобы волновые возмущения с пространственными периодами l_x * l , удовлетворяющими условию L = т_г • l , затухали (находились под нейтральной кривой T ( к ) ). Для циклогексана с добавками солей [29] (при £ = 2,2; K = 1,2 • 10 ^{- 8} см2 с/В; п = 0,979 •Ю^{- 3} Па^с;   V_o = 4,2 Кв) получим электрическое число Релея, равное

T = 6960, что соответствует интервалу значений T, в котором численное моделирование предсказывает существование бегущей волны. Таким образом, в геометрии кольцевых каналов шириной 1,3 d ^ 3 d и большим отношением радиуса к высоте следует ожидать появления волновых течений.

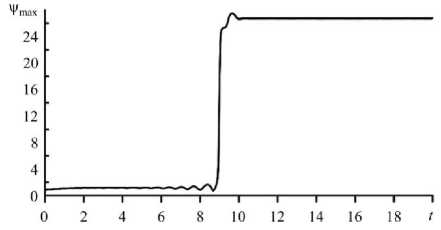
Рис. 12. Зависимость от времени максимального значения функции тока у^ при Т = 7070 ; переход от режима MTW к режиму SOC

• 4.4.    Режим стационарной конвекции SOC

  Область существования надкритических режимов заканчивается при T > Т_с4= 7061. При значениях электрического числа Релея, превышающих этот порог, надкритические слабоинтенсивные режимы конвекции теряют

• 4.5.    Бифуркационная диаграмма режимов движения жидкости

  

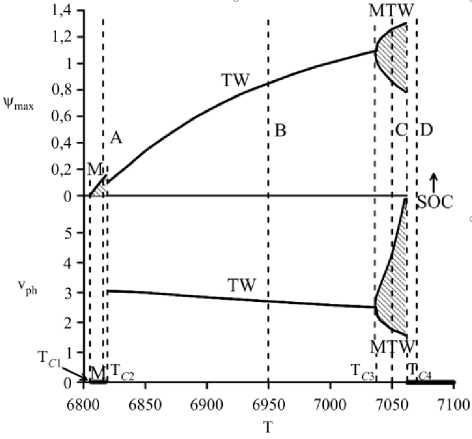
  Рис. 13. Бифуркационная диаграмма режимов электроконвекции: верхний график – зависимость максимального значения функции тока, нижний график – зависимость фазовой скорости бегущей волны; области соответствуют разделам данной статьи: А – 4.1, B – 4.2, C – 4.3, D – 4.4

  
  
  

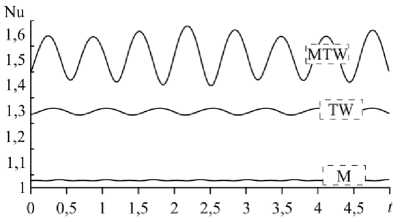
  Рис. 14. Эволюция числа Нуссельта в смешанном режиме (M), режиме бегущих волн (TW) и режиме модулированных бегущих волн (MTW)

  
  
5.    Влияние расчетной сетки на электроконвективные численные решения

устойчивость, и в системе скачкообразно происходит переход к режиму стационарной конвекции (SOC — Steady Overturning Convection) (Рис. 12). Данный режим отличается, во-первых, степенью интенсивности конвекции, которая в десятки раз выше, чем в надкритических режимах, рассмотренных ранее, а во-вторых, стационарностью в том смысле, что все рассматриваемые функции физической системы обладают постоянными во времени значениями. В ячейке располагаются два зеркально-симметричных конвективных вала, закрученных в противоположные стороны.

В результате исследования построена бифуркационная диаграмма режимов течения жидкости в зависимости от электрического числа Релея (Рис. 13). На диаграмме видно, что при увеличении электрического числа Релея в режиме TW интенсивность вращения жидкости в конвективных валах возрастает, а скорость горизонтального движения падает, в режиме же MTW растет амплитуда модуляций характеристик конвективного режима до тех пор, пока режим устойчив. Заштрихованные области означают, что при таких значениях управляющего параметра соответствующие характеристики системы с течением времени могут принимать значения из всего заштрихованного диапазона (проявляется временная модуляция параметров).

Изменение числа Нуссельта, которое характеризует соотношение между интенсивностью теплообмена за счет конвекции и интенсивностью теплообмена за счет теплопроводности (в условиях неподвижной среды) со временем для разных волновых режимов (разрезы A–C на Рис. 13) представлено на рисунке 14. Отметим, что средние по времени теплопотоки в этих режимах: Nu_M = 1,03 (разрез A), Nu_Tw= 1,28 (разрез B), Nu_MTw = 1,51 (разрез C), значительно ниже теплопотока для стационарной электроконвекции Nu_soс = 7,48.

Ранее электроконвекция в слабо-проводящей жидкости рассматривалась при нагреве сверху и униполярной инжекции, зависящей от напряженности электрического поля: q ( z = 0 ) = AE_Z [7].

Бифуркационная диаграмма в этом случае содержит решения не только виде бегущих волн, но и устойчивые решения для модулированных стоячих волн, которые в обсуждаемой здесь задаче отсутствуют. Следует отметить, что в обеих задачах (с постоянной инжекцией и с инжекцией, зависимой от электрического поля) на бифуркационной диаграмме есть общие особенности. Волновые режимы электроконвекции появляются в результате прямой бифуркации, а при достаточно больших значениях электрического числа Релея волновые решения становятся неустойчивыми, и возникает интенсивная стационарная электроконвекция.

Сетка с числом узлов 21 x 41, использовавшаяся для дискретизации расчетной области в основной части исследования, была выбрана не случайно: в задаче об электроконвекции, когда инжектированный заряд зависит от напряженности поля на электроде, рассматриваемой в безындукционном приближении

[7, 14, 15], показано, что измельчение сетки не приводит к качественному изменению бифуркационной диаграммы. Обсудим, как влияет число узлов сетки на характер решений. Далее в расчетах, кроме основной сетки (21 x 41 узел), применялись более подробные, с числом узлов 31 x 61 и 41 x 81.

• 5.1.    Пороги волнового и стационарного конвективных режимов

• 5.2.    Режим бегущих волн TW

  При изучении влияния числа узлов сетки на режим бегущих волн использовалось значение Т = 6950, соответствующее бегущим волнам на «грубой» сетке — сетке с числом узлов 21 x 41. Если взять вычисленные на ней распределения функций и пересчитать их для сетки с более мелким шагом с помощью метода продолжения по параметру, то можно получить зависимости от времени функций исследуемой системы на измельченных сетках: 31 x 61 и 41 x 81 узел.

Значения, при которых возникает колебательная конвекция в неподвижной жидкости (электрическое число Релея T , Рис. 13) или происходит переход к высокоинтенсивному режиму стационарной конвекции (SOC, электрическое число Рэлея Т_с4 , Рис. 13) для сеток 21 x 41 и 31 x 61 узлов приведены в таблице 1.

Таблица 1. Критические значения управляющего параметра T на разных сетках

Размер сетки Состояние системы	21 x 41	31 x 61	Относительная погрешность решения 2, %
	Значение 1	Значение 2
Возникновение конвекции	6805	6857	<1
Переход к SOC	7061	7050	<1

Как видно из рисунка 15, режим бегущих волн сохраняется и при более подробных сетках. Максимальное и минимальное значения функции тока в ячейке остаются практически постоянными, а значение функции тока в конкретной точке ячейки меняется гармонически, что соответствует бегущей волне или горизонтальному движению жидкости с постоянной скоростью. Фурье-спектры зависимостей значения функции тока в точке ячейки для разных сеток (см. Рис. 16) также практически совпадают. При измельчении сетки незначительно уменьшается интенсивность конвекции в расчетной ячейке (падает максимальное значение функции тока) и едва заметно возрастает скорость горизонтального движения жидкости.

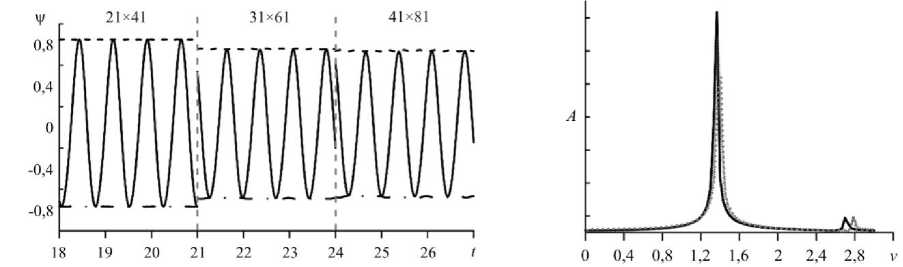
Рис. 15. Зависимости от времени значений функции тока на различных сетках в режиме TW при Т = 6950 : ψ (штриховая линия), в фиксированной точке ячейки ψ (сплошная линия) и ψ (штрихпунктирная линия)

Рис. 16. Фурье-спектры зависимостей значения функции тока в фиксированной точке ячейки ψ на сетках с разным числом узлов: 21 x 41 (сплошная линия), 31 x 61 (волнистая), 41 x 81 (кружки)

Распределения в ячейке функции тока, отклонений от равновесных значений заряда и температуры 0 при разных сетках представлены на рисунке 17. Данные распределения практически идентичны для каждого числа узлов, и даже на самой грубой сетке 21 x 41 узел на одну пространственную структуру функций приходится более десяти узлов сетки.

Сравнение количественных характеристик (максимального и минимального значений функции тока в ячейке, фазовой скорости горизонтального движения жидкости) в режиме TW при разных сетках приведено в таблице 2.

Таблица 2. Характеристики бегущей волны при разных сетках, T = 6950

Размер сетки	21 x 41	31 x 61		41 x 81
Характеристика	Значение 1	Значение 2	Относительная погрешность значения 2, %	Значение 3	Относительная погрешность значения 3, %
ψmax	0,847	0,756	= 11	0,743	= 11
ψmin	–0,767	–0,689	= 10	–0,671	= 13
vph	2,72	2,74	= 1	2,82	= 1

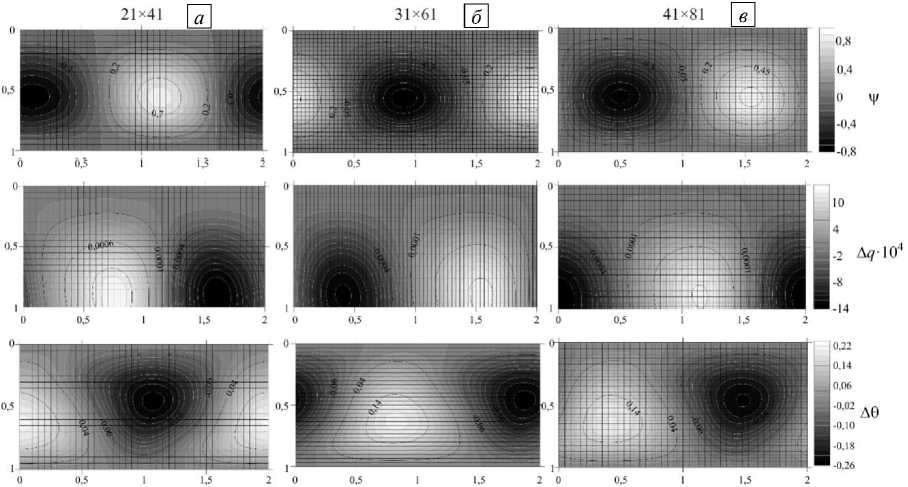
Рис. 17. Распределения в ячейке функции тока v , отклонений от равновесных значений заряда A q и температуры 6 при разных сетках, число узлов: 21 x 41 ( a ); 31 x 61 ( б ); 41 x 81 ( в ); черная сетка соответствует сетке численного метода; T = 6950

• 5.3.    Режим модулированных бегущих волн MTW

  Исследован режим MTW при T = 7040 как на «грубой» сетке 21 x 41 узлов, так и на измельченной, содержащей 31 x 61 узлов; рассмотрены: модуляция максимального и минимального значений функции в ячейке (Рис. 18), модуляции интенсивности конвекции в валах. В Фурье-спектре значения функции тока в точке ячейки появляется дополнительная частота, соответствующая модуляции колебаний (Рис. 19).

Если сравнивать режим MTW на разных сетках, то можно заметить, что при примерно одинаковых максимальной и минимальной возможных интенсивностях конвекции с переходом от крупной сетки

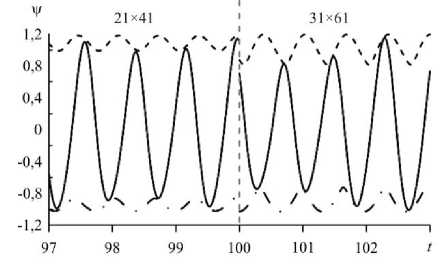
Рис. 18. Зависимости от времени значений функции тока: ψ (штриховая линия), в фиксированной точке ячейки ψ (сплошная линия) и ψ (штрихпунктирная линия) на разных сетках в режиме MTW, T = 7040

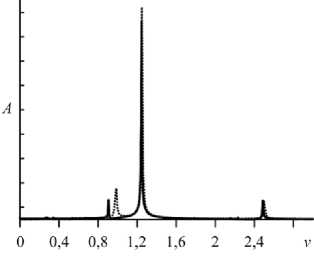
Рис. 19.   Фурье-спектры зависимостей значения функции тока в фиксированной точке ячейки ψ в режиме MTW при T = 7040 на разных сетках, число узлов: 21x41 (сплошная линия), 31x61 (пунктирная)

к мелкой больше становится амплитуда колебаний максимального и минимального значений функции тока, увеличивается частота модуляции, фазовая скорость жидкости меняется c большей амплитудой. Распределения же функций системы при модулированной бегущей волне в ячейке, как и в случае бегущей волны, практически идентичны на обеих сетках (Рис. 20). Для сравнения количественных характеристик (максимального и минимального значений функции тока в ячейке, минимальной и максимальной фазовой скорости горизонтального движения жидкости) в режиме MTW при разных сетках информация представлена в таблице 3.

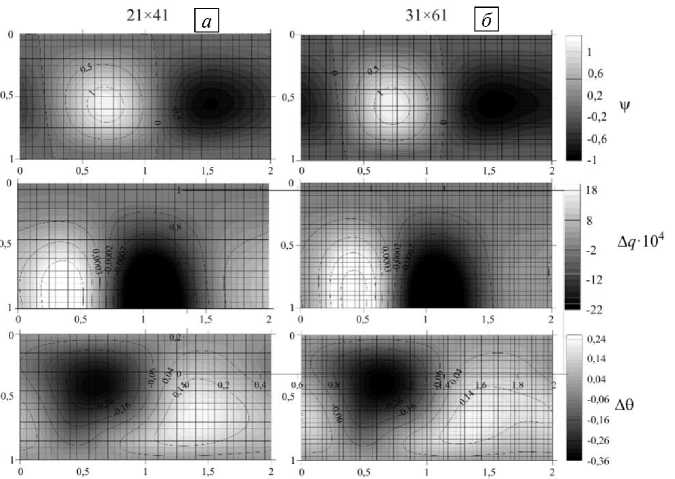
Рис. 20. Распределения в ячейке функции тока v , отклонений от равновесных значений заряда Д q и температуры 6 при разных сетках, число узлов: 21 x 41 ( a ), 31 x 61 ( б ); T = 7040

Таблица 3. Сравнение характеристик модулированной бегущей волны на грубой и измельченной сетке, Т = 7050

Размер сетки			21 x 41	31 x 61	Относительная погрешность значения 2, %
Характеристика			Значение 1	Значение 2
ψmax среднее			1,09	0,98	= 10
ψ   максимальное ψ max			1,18	1,20	= 2
ψ  минимальное max			0,99	0,81	= 4
ψmin среднее			–0,95	–0,87	= 8
ψ максимальное ψ min			–0,86	–0,72	= 16
ψ минимальное ψ min			–1,02	–1,03	=
	v ph	максимальное	3,2	3,8	= 19
	vph	минимальное	2,2	1,8	= 18

6.    Заключение

В результате численного моделирования на основе метода конечных разностей проанализирована эволюция двумерных режимов электроконвекции (смешанного режима, режимов бегущих волн, модулированных бегущих волн, стационарного режима), возникающих в нагреваемом сверху конденсаторе, заполненном слабопроводящей жидкостью. Предполагается, что свободный заряд образуется за счет автономной униполярной постоянной инжекции с катода.

Построена бифуркационная диаграмма решений и поля функции тока, температуры, заряда и потенциала для рассмотренных режимов. Смешанный колебательный режим большую часть периода представляет собой стоячую волну, которая дважды за период кратковременно переходит в бегущую волну, смещающую конвективную структуру в горизонтальном направлении на половину пространственного периода. Показано, что в режиме бегущей волны (TW) увеличение электроконвективного параметра T , характеризующего влияние электрического поля на заряженную жидкость, приводит к росту максимального значения функции тока, а следовательно, к увеличению интенсивности конвективного перемешивания жидкости; фазовая скорость горизонтального движения волны при этом уменьшается. При некотором критическом значении электроконвективного параметра T происходит переход к модулированной бегущей волне (в режим MTW), а затем — в режим стационарной конвекции (SOC).

Изучено влияние числа узлов расчетной сетки на характеристики электроконвективных режимов. Показано, что решения, полученные на грубой расчетной сетке (21 x 41) хорошо воспроизводятся на более подробных сетках.