Электрон Керра - Ньюмана как адаптивная система

Проблема объединения гравитации и квантовой теории является, по-видимому, главной нерешенной проблемой современной теоретической физики. Одним из подходов к решению проблемы взаимодействия гравитации и квантовой теории является теория суперструн, в которой элементарные частицы представлены собственными частотами протяженных объектов - струнами конечных размеров – суперструнами. Базовые выводы хорошо известны и до сих пор широко обсуждаются, хотя и подвергаются критике поскольку не подтверждаются и не приносят новых результатов. Альтернативой теории суперструн является петлевая квантовая гравитация. Как отметил один из основателей теории суперструн Дж. Шварц: "... с 1974 года теория суперструн перестала рассматриваться как физика частиц ... "и "... реалистичные модели элементарных частиц до сих пор кажутся далееекой мечтой ... "[1]. Третья парадигма – рассматривать черные дыры (источник гравитации) как элементарные частицы – предлагалась неоднократно с 1980 года, и с 1990-х годов она привлекла также внимание в теории суперструн. Интерес к поиску связи между черными дырами, струнами и элементарными частицами возобновился в сравнительно недавних работах [2, 3, 4, 5], и продолжается до настоящего времени [6].

Особенность этой парадигмы – в интерпретации элементарной квантовой частицы (электрона) как сверхвращающейся (параметр 7 〜 1) черной дыры Керра - Ньюмана(КН) [3, 8, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 19, 20]. Обсуждаемое нами в [1] решение для совместимой с КЭД моделью электрона как заряженной и сверхвращающейся черной дыры (ЧД) Керра – Ньюмана (КН), имеет согласно [30? ] следующий вид: появляются две различные метрики формы Керра – Шильда с твистом конгруэнции Керра: gj = / 叩 + Нк ^ к * и g ^— = 〃 丛“ + Нк~ - к - связанные с запаздывающим полем электрона и опережающим полем позитрона, где 〃 丛“ метрика плоского вспомогательного пространства Минковского (-+++), Н = (2тг - е ² )/г ² + q ² cos ² 仇 к * и к * - запаздывающая и опережающая конгруэнции Керра, связанные с полем излучения и полем входящей радиации. Развивая работу [30? ], мы анализируем точное решение, полученное Дебнеем, Керром и Шильдом (ДКШ) для с волнового электромагнитного поля и обнаруживаем, что оно было проинтегрировано в ДКШ не до конца, а только в предположении отсутствия электромагнитного излучения. Однако, при наличии излучения электронные (левые) и позитронные (правые) моды возбуждения кольцевой струны Керра не являются взаимно коррелированными в общем случае.

Это направление вновь оказывается связанным со струнной моделью, но это уже классическая релятивистская струна в 4-х измерениях, которая существенно отличается от суперструн многомерной квантовой гравитации.

Образование черных дыр связано с гравитационным эффектом затягивания пространства, который никогда ранее не рассматривался в физике частиц. Этот эффект оказывается действительно нетривиален и очень важен для понимания физической картины взаимодействия гравитации с квантовой теорией, поскольку он придает электрону дополнительную магнитную массу-энергию, порождаемую петлями Вильсона,– гравитационным затягиванием пространства во вращающуюся черную дыру КН [26].

Противоречие между квантовой теорией и гравитацией проявляются наиболее остро в теории электрона. Квантовая теория Дирака представляет электрон как точечный математический объект: гибрид волны и частицы, в то время как гравитация, требует протяженного распределения материи в пространствовремени. Предположение, что частицы являются черными дырами было впервые высказано независимо рядом известных физков, Нобелевскими лауреатами: Абдус Саламом (Abdus Salam), Франком Вильчеком (Frank Wilczek) и Геральд т Хофтом (Gerald ’t Hooft).

Однако, эти ранние идеи касались только решения Э. Шварцшильда, свойства которого очень далеки от свойств решения Керра для релятивистки вращающегося гравитационного поля, и практически не имели отношения к модели вращающейся черной дыры КН. Подход к черной дыры Керра как модели электрона начинается с работы Б. Картера [3] (1968), который обнаружил, что решение Керра - Ньюмена (метрика Керра с зарядом) имеет гиромагнитное отношение (g = 2) такое же, как у модели электрона Дирака.

В отличие от гравитационного радиуса решения Швацшильда ls =巻,эффективная зона гравитационного взаимодействия в решении КН определяется радиусом керровского сингулярного кольца

J q =-me

(0.1)

который обратно пропорционален массе m и прямо пропорционален угловому моменту решения Керра J.

Для параметров электрона с массой m и спином J =方/2, параметр q является половиной длины волны Комптона а = 2^, и обычные аргументы об исключительной роли планковской длины (см., например, [22]) оказываются недействительными при их применении к вращающейся гравитации Керра.

К числу дополнительных неожиданностей, связанных с моделью электрона как черной дыры Керра –Ньюмена (КН), являлась ее "неточечность". Связанная с электроном, длина волны Комптона возникла как бесплатное приложение, обусловленное параметром вращения решения Керра (0.1). В координатах Керра – Шильда, связанных с ассиптотически плоским пространством Минковского, решение КН описывается как классическое гравитационное поле кольцевой струны половины комптоновского радиуса а.

На комптоновский размер электрона указывал также В. Израэль [10], и позднее К. А. Лопез [11] и др., и это совсем не безобидный факт, поскольку комтоновский масштаб 10 ^-11 см, являясь естественным масштабом для физики частиц, превышает планковский масштаб 10 ^-33 см на 22 порядка, на котором основаны как квантовая петлевая гравитация, так и теория суперструн.

Вслед за Картером, модель электрона КН была детально рассмотрена в фундаментальной работе Дж.С. Дебнея, К.Р. Керра и А. Шильда (DKS) [8] и далее в важных работах [10] и [11], а также в моделях [12, 13, 23], основанных на идее Дж. Уиллера "массы без массы "и аналогии сингулярного кольца Керра с классической струной Нильсена–Олесена [24], возникающей в виде сингулярной нити в теории сверхпроводимости.

Эти работы были учтены в последующей серии работ [15, 16, 17], в которой модель электрона рассматривалась как сверхпроводящий "мешок имеющий форму очень тонкого сверхпроводящего диска Керра с толщиной ^ а/137 и радиусом а, равным половине комптоновской длины волны электрона, см. Рис.1. Диск Керра, искажая пространство, образует вакуумный сгусток – "ядро"электрона, окаймленное двумя петлями Вильсона (электронной и позитронной), которые формируются гравитационным затягиванием электромагнитного поля. Модель электрона KН согласована с классической гравитацией по своей природе, как точное решение системы уравнений Эйнштейна-Максвелла [8], и исследование структуры этой модели связано с разрешением известных ранее непреодолимых противоречий между гравитацией и квантовой теорией. В частности, утверждений:

• (1)    точечный, бесструктурный электрон квантовой теории не совместим с гравитацией;

• (2)    протяжённый гравитирующий электрон не совместим с квантовой теорией.

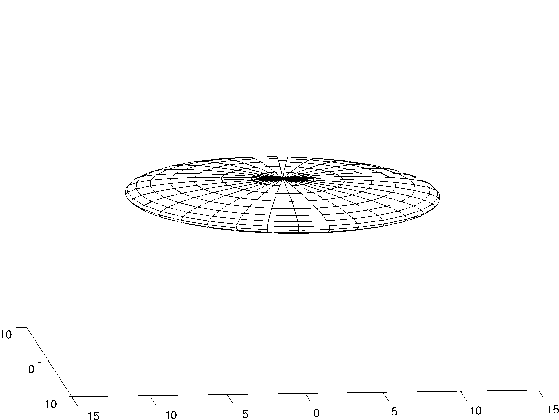
Рис. 1. Дискообразное ядро электрона КН, однозначно определяемое формой решения КН и эллипсоидальной системой координат Керра-Шильда [8].

Плоскость, в которой лежит сингулярное кольцо Керра, служит границей расщепления пространства на два листа, и решение КН с параметрами электрона не является на самом деле черной Ды^рой, потому что для типичных вращающихся элементарных частиц @ 2 》 е ² + ш 2 , что приводит к условию исчезновения горизонтов черной дыры, а это значит, что обнаженное сингулярное кольцо Керра оказывается голым. Как следствие, тензор энергии-импульса сингулярного кольца Керра расходится, и сверхвращающееся кольцо Керра несёт бесконечную энергию, которая нуждается в регуляризации (и даже в перенормировке) в соответствии с КЭД.

Введенный Лопезом параметр обрезания %, определяет приращение векторного потенциала КН вдоль замкнутых петель Вильсона [25, 26, 27], что ведущее к балансу между гравитационным и электромагнитным взаимодействиями, определяя регуляризированную массу частицы как результат нелинейного гравито-электромагнитного взаимодействия. Электрон Лопеза, образует диск толщиной 2г _е и радиусом а, равным половине длины волны Комптона (0.1), см. Рис.1.

При этом, ядро регуляризованного электрона приобретает внутреннюю метрику пространства Минковского,сохраняя внешнее гравитационное и электромагнитное поле решения КН.

Кроме того, параметр обрезания 山， порождает две граничные поверхности диска Керра г ± , электронную и позитронную (см. Рис.3,4), которые формируются суперсимметричным фазовым переходом механизма Хигса [28] и играют важную роль в формировании единой квантовой вакуумной системы. При этом, как было показанно в [29, 30] соответствующие петли Вильсона формируют сильную магнитную связь между электронной и позитронной частями вакуумного ядра.

При этом, появление двух различных механизмов формирования массы-энергии электрона, объясняет физический смысл отдельного анализа голого и одетого электрона.

Голый электрон строится путем регуляризации классического стационарного решения КН в виде кольцевой безмассовой релятивистской струны, которая приобретает массу и сжимается в точечный электрон за счет релятивистского вращения. Волновые возбуждения струны порождают квантовую волновую функцию электрона в представлении В. Гейзенберга, удовлетворяющую уравнению Э. Шредингера.

Одетый электрон порождается суперсимметричной моделью Гинзбурга-Ландау, в процессе фазового перехода к регуляризованному вакуумному состоянию. Масса-энергия одетого электрона рождается из бесконечной энергии регуляризованного сингулярного электрона Керра под влиянием полей Хиггса, формирующих фазовый переход к сверхпроводящему ядру – области сильного магнитного взаимодействия электронного и позитронного вакуума.

Модифицируя исходное решение КН, Израэль и Лопез [4,5] отсекали отрицательный лист решения КН. В докладе [1] обсуждалась иная модификация решения КН, с заменой отрицательного листа решения на зеркальный лист, с одновременным отражением конгруэнции от тяжелого ядра электрона, формируемого полями Хиггса. Зеркальный лист интерпретируется как позитронный лист электронно-позитронного вакуума одетого электрона согласно КЭД, [1]. Эта интерпретация поддерживается также известной старой интерпретацией о порождении заряда электрона стационарным ЭМ полем запаздывающего потенциала и законом сохранения заряда электроннопозитронного вакуума. Запишем уравнение Эйнштейна в метрике Керра – Шильда [8]

冗 Н"

с4 “,

(0.2)

где Л _М" - тензор Риччи, определяемый симметричным метрическим тензором д ^" ； 〃“ - тензор энергии-импульса материи; c – скорость света в вакууме; G – гравитационная постоянная Ньютона. В уравнении (3) правая часть описывает энергию стационарных гравитационного и электромагнитного полей, формирующих кольцевую релятивистскую безмассовую струну голого электрона, порожденную увлечением вектор-потенциала (frame-dragging) гравитационным полем КН с твистом конгруэнции Керра, рис.1.

Это решение имеет соответствующий экспериментальным данным д-фактор (равный 2) для электрона [3, 8], и описывает структуру электрона КН, моделируя непертурбативный гравитирующий

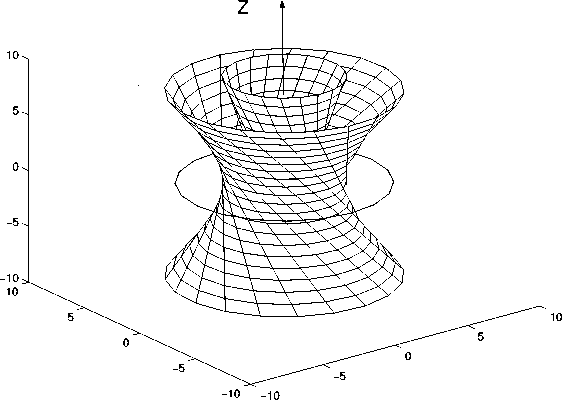
Рис. 2. Конгруенция Керра переходит аналитически через сингулярное кольцо Керра на отрицательный лист метрики КН.

электрон [3, 10, 11] и процесс взаимодействия электрона с полями Хиггса и гравитацией, который регуляризует электронно-позитронный вакуум согласно КЭД [30]. Заметим, что полученное в фундаментальной работе Керра, Дебнея и Шильда [8] точное решение было доведено до кон- ца лишь при условии отсутствии 7 = 0 (см. [8] (5.51)), что как было выяснено позже в работе

[][8] (АБ 2003) соответствует стационарному решению КН без излучения ЭМ поля. Решения КН с излучением, полученные в работе [8] для выходящей конгруэнции к+ показали, что параметр

7+ имеет смысл ЭМ излучения в направлении к+, и соответствующая часть энергии излучения т£” = |7+|2(к〃+к+)/2

равна

. Подобным образом, поглощение ЭМ поля, входящего с направле- ния к-, описывается заменой 7+ на 7-, и конгруэнции kj на к-. Следовательно, точное решение КН является стационарным и рассмотренная в [1] модель электрона как кольцевой струны Керра не излучает и не поглощает энергию ЭМ поля. Это является существенным недостатком рас- смотренной ранее модели, которая в остальных отношениях очень важна, поскольку описывает согласованное с КЭД стационарное кольцевое состояние как голой, так и одетой релятивистской струны электрона, а также, связанной с ядром электрона позитронной струны электрона, и обе струны взаимодействуют с гравитацией и с полями Хиггса путем формирования двух магнитносвязанных петель Вильсона [1].

Вектор-потенциал ЭМ поля в электронной петле А+ = -((У+,т +)/(厂 + iacos^))к+ приобретает дополнительную зависимость от У+ (поворот по углу д), порождая излучение электрона КН, и одновременно воздействуя на аксиальный входящий луч к— позитронной петли, возбуждая входящее ЭМ поле, как обратную связь осциллирующей электронно-позитронной системы. Эта корреляция между возбуждениями ЭМ поля в электронной и позитронной петлях, настраи- вает связь между положениями и направлениями соответствующих полуструн и индуцируемыми вблизи них полями, включая частоту колебаний и их фазы, сопоставляя исходящему электронно-

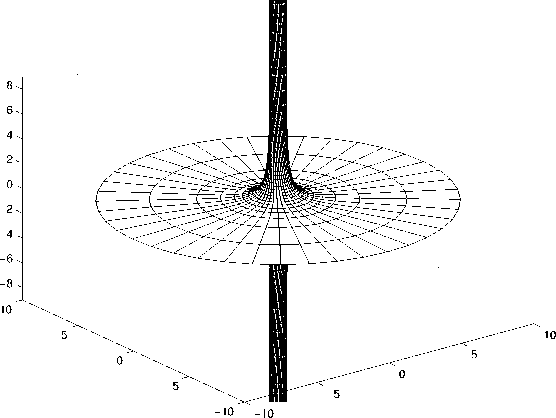
Рис. 3. Аксиальный сингулярный луч, направляющий выходящее ЭМ поле, в решениях с излучением 7 + .

му лучу левую моду осцилляции с левой комплексной полуструной, а входящему позитронному лучу — правую комплексную полуструну, устанавливая между ними связь струнной операцией, известной как ориентифолдизация.

Таким образом, общее решение КН, учитывающее как ЭМ поле излучения, связанное с параметром 7 + , так и входящее ЭМ поле с параметром 7 - , связывает правые и левые моды возбуждения электронной и позитронной петли. Аксиальный луч, совместно с кольцевой сингулярностью Керра действуют как узко направленная антенна, которая усиливает излучаемое ЭМ поле, а также отраженный сигнал входящего ЭМ поля, поступающий в соответствующую позитронную ветвь решения КН. Нами выдвигается гипотеза, что непертурбативный электрон КН является аналогом минимальной адаптивной системы, которая способна просматривать и оценивать окружающую обстановку передачей и приемом электромагнитного излучения и вырабатывать обратную связь (сигнал ошибки) для управления направлением движения электрона согласно принципу наименьшего действия. В хорошо известном квантовом опыте с двумя щелями, волна де Бройля, сопутствующая падающей частице (волны-пилота), дифрагирует на щелях, а затем создает интерференционную картину сложения двух частей первоначальной волны, свидетельствуя о загадочной сверх информированности электрона о состоянии щелей. Непертурбативная модель электрона КН, снабженная аксиальной структурой излучающей и принимающей ЭМ поле, показывает, что волновая функция электрона Дирака генерируется ЭМ полем, связанным с релятивистским вращением электрона. Аксиальная сингулярная струна генерирует устойчиво направленное ЭМ поле, которое излучается кольцевой электронной струной, действующей как узконаправленная передающая антенна. Отраженное от пластины с двумя параллельными щелями ЭМ поле принимается "позитрон-ной"струной решения КН, действующей как приемная антенна для входящего ЭМ сигнала. При этом, аксиальная струнная система, подчиненная структуре ориентифолда, автоматически согласует излучаемый и приходящий сигнал по направлению, частоте и фазе, формируя согласованную приемо-передающую систему. Предположительно, интерференция скоррелированных переданного и принятого сигналов может формировать обратную связь и вырабатывать сигнал ошибки. Таким образом, в модели ЭМ поля электрона КН, являющейся развитием модели волны-пилота де Бройля – Бома, электрон "прощупывает"ЭМ полем окружающее пространство, и "видит"топологию пластины. Иначе говоря, он действует как простейшая самоорганизующаяся адаптивная система, выбирая оптимальный путь в соответствии с принципом наименьшего действия.

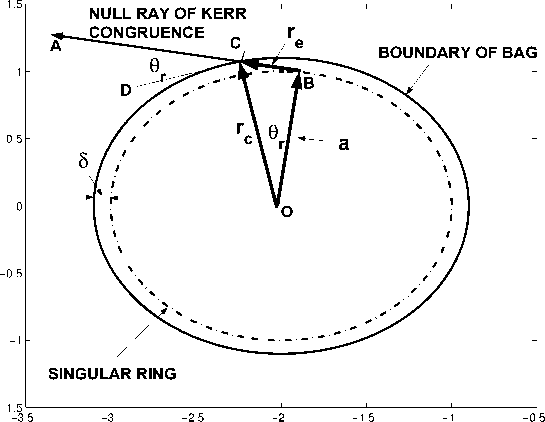
Рис. 4. Сингулярное кольцо электрона КН модифицируется добавлением аксиальной струны, в виде двух полуструн, согласуемых исходящим и входящим излучением

Заключение

Выше было показано, что понимание важности взаимодействия в модели электрона КН привело к определяемого вакуумным вкладом в виде двух сопряжённых петель Вильсона с зеркальными сторонами решения КН. Была выдвинута гипотеза, что непертурбативный электрон КН является аналогом минимальной адаптивной системы, которая способна просматривать и оценивать окружающую обстановку передачей и приемом электромагнитного излучения и вырабатывать обратную связь (сигнал ошибки) для управления направлением движения электрона согласно принципу наименьшего действия. Отметим также, что новая точка зрения на решение Керра - Ньюмана устанавливает тесную связь геометрии КН с теорией твисторов и теорией суперструн на комптоновском масштабе в соответствии с основным соотношением решения КН а = J/ 2 m, увеличивая реальный масштаб гравитационного взаимодействия с релятивистским электроном с предполагаемой ранее планковской длины 10 ^-33 см до комптоновской длины 10 ^-11 см, т.е. на 22 порядка.

В новой модели КН электрона проявляется физический смысл используемого в КЭД разделения массы-энергии элекрона на массу "голого"электрона, отвечающего за его волновые свойства, и гравитационно "одетого"электрона, генерирующего самосжимаемую массу-энергию сгустка "яд-ра"окружающего электрон поля, асоциируемого с "темной энергией". Сделан вывод, что все основные проблемы, связанные с совместимостью структуры гравитации со строением элементарных частиц находят решение в модели Керра – Ньюмана для сверхвращающейся (фактор Лоренца ∼ 1) ЧД с излучением, показывая совместимость модели электрона КН с квантовой теорией в представлении Гейзенберга, а также с моделью элементарной частицы, основанной на классической модели кольцевой струны Керра-Ньюмана как решения уравнений Максвелла – Эйнштейна.