Электронное строение и энергетический спектр двумерных ковалентных структур с локальными дефектами

Автор: Литинский Аркадий Овсеевич, Растова Наталья Александровна

Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu

Статья в выпуске: 10, 2006 года.

Бесплатный доступ

Модели кластера с граничными атомами водорода и циклического кластера и метод функционала плотности в валентном базисе STO-3 G (с учетом псевдопотенциала остовных электронов) применены для изучения особенностей электронного строения и энергетического спектра двумерных алмазоподобных ковалентных структур (на основе алмаза, кремния, германия) с выделенной поверхностью, покрытой атомами водорода (в 111-направлении). Обсуждены эффекты, обусловленные поверхностными дефектами замещения Элемент-Н (Э-Н) на атомы B, Al, Ga и атомов Н на атомы F и Cl.

Короткий адрес: https://sciup.org/14968579

IDR: 14968579

Текст научной статьи Электронное строение и энергетический спектр двумерных ковалентных структур с локальными дефектами

А.О. Литинский, Н.А. Растова

Модели кластера с граничными атомами водорода и циклического кластера и метод функционала плотности в валентном базисе STO-3G (с учетом псевдопотенциала остовных электронов) применены для изучения особенностей электронного строения и энергетического спектра двумерных алмазоподобных ковалентных структур (на основе алмаза, кремния, германия) с выделенной поверхностью, покрытой атомами водорода (в 111-направлении). Обсуждены эффекты, обусловленные поверхностными дефектами замещения Элемент-Н (Э-Н) на атомы B, Al, Ga и атомов Н на атомы F и Cl.

Двумерные ковалентные структуры (ДКС) могут служить основой для материалов микро-и наноэлектроники. Для конструирования элементов соответствующих приборов важно иметь представление об их электронном строении и энергетическом спектре электронов как идеальных, так и структур, содержащих локальные дефекты. В данной работе рассмотрены ДСК, в основе которых несколько слоев (вдоль 111-направления) алмазоподобных кристаллов (алмаз, кремний, германий), с обоих сторон которых нескомпенсированные валентности замкнуты атомами водорода (двухсторонний гидридный покров).

Для расчета требуемых ДКС использовались модели молекулярного кластера в форме расширенной элементарной ячейки (РЭЯ): а) с замыканием оборванных связей атомами водорода (РЭЯ-Н); б) с наложением циклических граничных условий (РЭЯ-ЦГУ) (рис. 1, 2). РЭЯ выбрана размером (3 х 3 х 3) = 27 элементарных (содержащих два атома) ячеек: три слоя из 9 поверхностных ячеек каждый. Локальные дефекты на поверхности вводились путем изовалентного замещения: а) группы Э-Н в центре поверхностной грани кластера на атомы B, Al, Ga (см. рис. 1–4), а также б) атома Н на F, Cl. Оптимизированные длины связей между атомами структур приведены в таблице 1.

Расчеты выполнены с применением неэмпирического метода функционала плотности [1, 2] в гауссовском базисе STO-3G [3] (атомные орбитали слэтеровсого типа представлены в виде линейной комбинации трех орбиталей гауссовского типа). Для атомов H, B, C, F в базис включены все орбитали, занятые в основном состоянии (начиная с 1s – АО), а для атомов Al, Cl, Ga в базис включены только валентные орбитали s - и p -типа. Учет влияния внутренних (остовных) электронных оболочек осуществлялся введением остовного псевдопотенциала [4, 5], то есть энергия взаимодействия j -го валентного электрона с остовом N-атомной системы представлялась в виде

N wmm (j) = Z W (A)(j)

A = 1

где W ⁽ ^A ⁾ – модельный потенциал, относящийся к остову атома А.

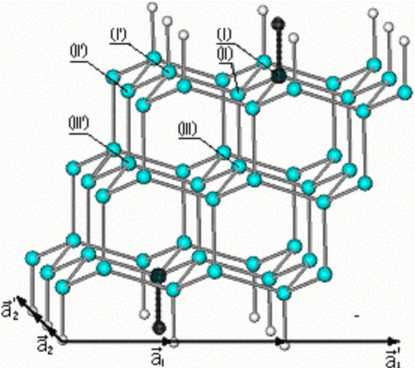
Рис. 1. Расширенная элементарная ячейка (РЭЯ) алмазоподобной ДСК с гидридным покровом <а,.Э_г-вектора элементарных трансляций;

3,3_С вектора трансляций РЭЯ);

(выделены поверхностные группы, замещаемые

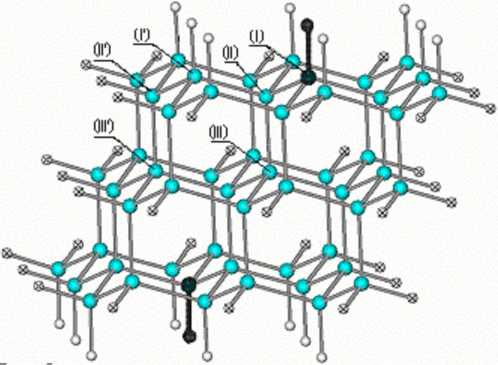
Рис. 2. Кластер РЭЯ-Н, моделирующей алмазоподобную ДСК с гидридным покровом (выделены поверхностные группы, замещаемые дефектами; я -атомы водорода замыкающее оборванные валентности в направлениях "параллельных” поверхности)

дефектами; Q - атомы алмазоподобной структуры; О - поверхностные атомы водорода)

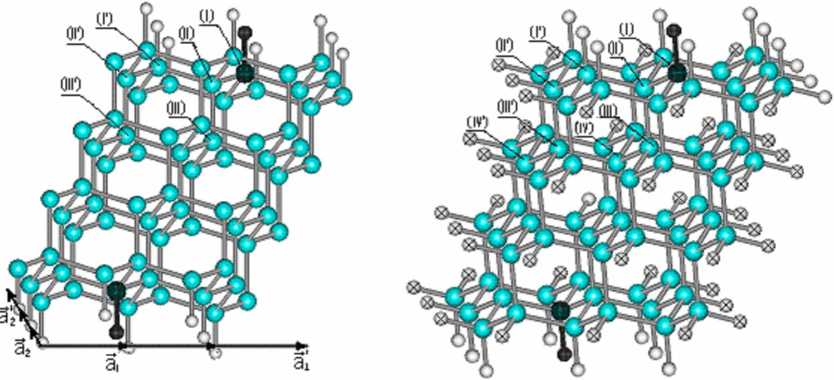
Рис.З. Расширенная элементарная ячейка (РЭЯ) алмазоподобной ДСК с гидридным покровом (Э,.а_г-вектора элементарных трансляций;

3,3Г вектора трансляций РЭЯ);

(выделены поверхностные группы, замещаемые дефектами; 0 - атомы алмазоподобной структуры;

О - поверхностные атомы водорода)

Рис.4. Кластер РЭЯ-Н, моделирующей алмазоподобную ДСК с мдридным покровом (выделены поверхностные группы, заметаемые дефектами; я - атомы водорода замыкающее оборванные валентности в направлениях "параллельных" поверхности)

Оааееоа 1

R (AB) (А) 1ажа6 aoiiaie а дапп^еоиааашо подбеобдао

э	Э-Э	в	Д1	Ga
с	1,54	1,59	1,95	2,03
Si	2.23	1,93	2,22	2,37
Ge	2,43	2.04	2.33	2.78

В соответствии с теорией функционала плотности (ТФП) [1, 2], молекулярные орбитали (МО) валентных (или любых) электронов ф j ( r ) находятся решением одноэлектронного уравнения Шредингера (в атомных единицах)

( - 2 V ² + и эфф ( r ) - 8.)ф . ( r) = 0,

где - ^ V

Е j υэфф(r)

оператор кинетической энергии электрона;

энергии МО ф j ;

эффективный потенциал, содержащий три члена:

иэфф(7) = и( r) + J

n ( Г ')

|r - r'\

-dr ' + u xc ( Г )

где u ( r ) - потенциал, обусловленный притяжением электронов к остовам (или к ядрам) (без учета взаимодействия электронов); второй член в (3) – кулоновское взаимодействие электрона в состоянии ф ( r ) с другими электронами; u xc ( r ) - локально-корреляционный потенциал, функционально зависящий от полного распределения электронной плотности n ( r ) в соответствии с выражением

^U xc ⁽ r ) =

au n (r)]

8 (n (r))

n ( 7 ) = n ( r ) ,

N υ

ⁿ ⁽ ⁷ ⁾ = Z | ф . ⁽ ⁷ ⁾|

j = 1

где N _u - число валентных (или всех) электронов, Е ^ n ( r ) J - функционал обменно-корреляционной энергии, выбранный в нашем случае в соответствии с [4, 5]. Самосогласованные уравнения ТФП (2)-(5) (уравнения Кона - Шэма) решались по программе Gaussian-03 [6]. В них МО ф _j ( r ) представляются в виде разложения по АО всех атомов системы

где АО χ_µ ⁽ ^A ⁾ локализована на атоме А , поэтому уравнение (1.2) эквивалентно задаче на собственные функции (матрица C _ц . ) и собственные значения е . оператора Хартри - Кона - Шэма

F = — ^ V ² + о_зфф , с ^ . ( F ^v - 8 j S ^u ) = ⁰ ,

где F _цu = Х^ц F |x_v) - матричные элементы оператора F- в базисе АО х _ц , S ^u = ( Х ц X?) - интегралы перекрывания АО / _ц и x _v .

Наложение циклических граничных условий на РЭЯ, а следовательно и на МО ф. (r), означает, что FµAνB, а также двухатомные члены, входящие в FµAνB и FµAµA , рассчитываются в соответствии с Хц и xv, локализованными на A и B (A е РЭЯ, B е РЭЯ), если расстояние между этими атомами не превышает радиуса взаимодействия R0 (= 1/2 размера РЭЯ). Если же R(A, B) > R0, то F^A^B сле- дует заменить на F^B, где атом B* эквивалентен атому В из соседней РЭЯ, причем fB, = rB +t, где f - подходящий вектор трансляции, переводящий атом B в B', такой, что R(A, B') < R0 (t = m1 tx + m2f, m 1, m2 - целые числа; f, E, - базисные векторы РЭЯ двумерной решетки).

Распределение зарядов q ( A ) на атомах различных слоев (рис. 1–4) для моделей РЭЯ-Н и РЭЯ-ЦГУ (см. табл. 2–5) свидетельствует о том, что в обоих случаях эти величины отличаются незначительно. Для атомов третьего слоя (III, III ' ) q ( A ) близки к нулю (соответствуют атомам объемной структуры). Наиболее чувствительны к влиянию поверхностного Н-покрова (или атомов поверхностных дефектов) атомы I слоя; в меньшей степени это влияние ощущают атомы II слоя. Расширение кластера в сторону увеличения числа слоев (на одну двухатомную ячейку) (см. рис. 3, 4; табл. 2, 3) качественно не изменяет результаты расчета, поэтому переход к моделям большего размера нецелесообразен.

Спектры одноэлектронных состояний (см. рис. 5–8), полученные для моделей а) РЭЯ-Н и б) РЭЯ-ЦГУ, отличаются тем, что в случае бездефектных структур для модели «б» энергия, отвечающая верхней границе занятых состояний (ЗС), повышается, а энергия, соответствующая нижней границе вакантных состояний (ВС), понижается. Это связано с тем, что число «объемных» атомов в рассчитываемой модели увеличивается (в модели РЭЯ-ЦГУ все атомы Э одного слоя эквивалентны между собой, а в модели РЭЯ-Н часть этих атомов становится граничными, то есть неэквивалентными объемным).

Зоне занятых состояний (ЗЗС) отвечают энергии связывающих Э-Э- и Э-Н-орбиталей, причем Е _связ (С-Н) отстоят от верхней границы (ВГ) ЗЗС на величины порядка 50-90 % от ширины запрещенной щели (ЗЩ) N E g . Зоне вакантных состояний (ЗВС) соответствуют энергии разрыхляющих орбиталей Э-Э- и Э-Н-связей, причем е _разр (С-Н) отстоят от нижней границы ЗВС на величины порядка 70-90 % от N E g .

Схемы уровней энергий электронов, полученных для обеих моделей в случае структур с локальными дефектами на поверхности, представлены на рисунках 5–8. Анализ рассчитанного спектра одноэлектронных состояний позволяет сделать следующие выводы:

1. В случае B-, Al-, Ga-поверхностных дефектов:

а) в спектре появляются состояния, обусловленные ими, энергии которых лежат в запрещенной энергетической щели (ЗЭЩ) и отстоят от нижней границы ЗВС на величины, перечисленные в таблице 5. Как следует из этой таблицы, акцепторные состояния, обусловленные атомами дефектов, оказываются примерно в центре ЗЭЩ, причем наиболее глубокое проникновение этих состояний имеет место в случае внедрения атома Ga в поверхностную ДКС на основе алмаза;
б) имеются также состояния, обусловленные связывающими орбиталями Д-Э-связей (проникают вглубь ЗЗС) и разрыхляющими орбиталями этих связей (проникают вглубь ЗВС) (табл. 6). Как следует из этой таблицы, степени проникновения этих состояний в соответствующие энергетические зоны зависят от природы атома дефекта (Д) и изменяются в пределах от 10 до 80 %.
2. Для F-, Cl-замещений атомов Н гидридного покрова:

а) в спектре появляются состояния, обусловленные орбиталями неподеленных пар атомов галогенов, причем для F эти состояния оказываются в ЗЭЩ и проникают в нее на 5–10 % (ДКС-С), 8–12 % (ДКС-Si) и 4–8 % (ДКС-Ge); для Cl эти состояния преимущественно локализованы в области энергий, соответствующих верхней границе ЗЗС;
б) что касается состояний, отвечающих связывающим и разрыхляющим орбиталям Э-F и Э-Cl-связей, (табл. 6), то в этом случае остаются качественно справедливыми выводы, отмеченные в п. 1б для B-, Al-, Ge-дефектов.

Таблица 2

Заряды на поверхностных атомах водорода и атомах ДКС в слоях I, II, III двумерных поверхностных структур (идеальных и с поверхностными локальными дефектами) [по результатам расчета в рамках РЭЯ-Н и РЭЯ-ЦКЛ-моделей]

	э=с
	без дефекта		поверхностный дефект
	без дефекта		В		AI		Ga
	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ
q( Н )	0,068	0,667	-	-	-	-	-	-
q( Э¹)	-0,073	-0,073	0,286	0,278	1,224	0,879	0,580	0,556
q( Э-)	0,007	0,006	-0,083	-0,086	-0,332	-0,284	-0,197	-0,196
q( Э")	0,000	0,000	0,008	0,008	0,001	0,011	0,013	0,013
q( э^г)	-0,070	-0,073	-0,070	-0,072	-0,079	-0,065	-0,064	-0,066
q( э')	-0,071	0,006	-0,071	-0,083	-0,332	0,072	-0,073	-0,197
q( Э'")	0,007	0,000	0,009	0,008	0,002	0,004	0,006	0,013
q( HJ	0.069	0,667	0.084	0,059	0,043	0,067	0,069	0,065
					Si
			поверхностный дефект
	ugj декрета		В		Al		Ga
	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ
q( H )	-0,117	0,122	-	-	-	-	-	-
qO¹)	0,108	-0,096	0,324	0,470	0,587	0,703	0,450	0,588
q( Э')	0,016	-0,238	-0,109	-0,139	-0,116	-0,221	-0,116	-0,152
qO"')	0,002	-0,002	0,012	-0,002	-0,007	-0,005	-0,007	-0,005
q( э^г)	0,113	-0,096	-0,120	-0,109	-0,127	-0,110	-0,128	-0,109
q(	0,113	-0,238	-0,110	0,138	-0,120	-0,221	-0,121	-0,152
q( Э”)	0,016	-0,002	-0,001	-0,002	-0,013	-0,005	-0,012	-0,005
q( H )	-0,117	0,122	0,124	0,118	0,124	0,114	0,125	0,115
				Эе	EGe
			поверхностный дефект
	uej декрета		В		Al		Ga
	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ
q(H )	0,119	0,119	-	-	-	-	-	-
qO¹)	-0,116	-0,114	0,474	0,473	0,570	0,555	0,407	0,392
qO')	-0,003	-0,003	-0,199	-0,148	-0,160	-0,160	-0,106	-0,107
q( Э")	-0,001	-0,001	0,004	0,005	0,000	0,001	-0,001	0,000
q( э^г)	-0,117	-0,114	-0,123	-0,120	-0,125	-0,123	-0,125	-0,122
q( 3"')	-0,012	0,003	0,119	-0,148	-0,117	-0,160	-0,117	0,107
q( Э'")	-0,029	-0,001	-0,001	0,005	-0,004	0,001	-0,003	0,000
	0,114	0,119	0,119	0,116	0,116	0,115	0,117	0,116

Таблица 3

Заряды на поверхностных атомах водорода и атомах ДКC на основе германия в слоях I, II, III, IV двумерных поверхностных структур (идеальных и с поверхностными локальными дефектами)

[по результатам расчета в рамках РЭЯ-Н и РЭЯ-ЦКЛ-моделей]

	3=Ge
	без дефекта		поверхностный дефект
	без дефекта		В		AI		Ga
	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ	РЭЯ-Н	РЭЯ-ЦКЛ
q(H )	0.113	0.119	-	-	-	-	-	-
q( Э¹)	-0,116	-0.114	0,472	0,472	0,569	0,553	0,406	0,391
q( 3')	-0,003	-0,004	-0,149	-0,149	-0,160	-0,160	-0,106	-0,107
qO¹")	-0,003	-0,002	0,002	0,005	-0,003	0,000	-0,004	0,000
q( 3^IV)	0,000	0,001	0,002	0,002	0,002	0,001	0,002	0,002
q( Э^г)	-0,226	-0,114	-0,231	-0,121	-0,238	-0,123	-0,238	-0,123
q( 3')	-0,003	-0,004	-0,162	-0,148	-0,162	-0,160	-0,109	-0,107
q(	-0,116	-0,002	-0,105	0,003	-0,113	-0,001	-0,110	-0,002
q( 3^IV)	-0,003	0,001	-0,002	0,001	-0,005	-0,001	-0,004	0,000
q(H)	0,119	0,119	0,111	0,116	0,110	0,115	0,110	0,116

Таблица 4

Энергии, отвечающие границам занятых и вакантных состояний

(е ВЗМО е НЕМО соответственно); ширина верхней валентной зоны D E V (p) и степени проникновения состояний, отвечающих связи С-Н, в зону занятых состояний и в зону вакантных состояний (в % от ширины запрещенной щели)

[для ДКС на основе алмаза (С), кремния (Si) и германия (Ge)]

	С		Si		Ge
	РЭЯ-Н	РЭЯ-ЦГУ	РЭЯ-Н	РЭЯ-ЦГУ	РЭЯ-Н	РЭЯ-ЦГУ
^Евзмэ. эВ	6,60	5,68	-6,86	-5,83	-6,19	-5,29
^нгмо.эВ	-3,32	-1,64	-0,93	-1,14	-0,95	-1.73
ЛЕ^.эВ	6.8	6,2	4.9	4,0	5.4	4,1
<5„(С-Н). %	75	52	57	52	98	77
5^С-Н). %	82	67	71	63	106	89

Таблица 5

Глубина проникновения (в % от D E_g ) локальных акцепторных состояний в запрещенную энергетическую щель

ДКС	дефект замещения
	В		А!		Ga
	РЭЯ-Н	РЭ Я-ЦРУ	РЭЯ-Н	РЭЯ-ЦГУ	РЭЯ-Н	РЭЯ-ЦГУ
с	65	66	68	27	66	71
Si	46	36	57	47	52	46
Ge	49	41	61	56	58	53

Таблица 6

Глубины проникновения состояний, обусловленных связывающими орбиталями Д-Э связей в ЗЗC (в % от D E_v ^(p) ) и разрыхляющих состояний в ЗВC (в % от D E_g ) (по данным расчета моделей ДКС с соответствующими поверхностными дефектами)

ДКС на основе С
модель	РЭЯ-Н		РЭЯ	-ЦГУ
дефект	в ЗЗС	в ЗВС	в ЗЗС	в ЗВС
В	36,31	30,07	41,27	42,78
AI	27,24	35,51	27,60	53,70
Ga	29,96	35,31	45,65	25,01
F	29,46	32,99	45,92	34,30
Cl	42,53	24,02	52,89	23,51
ДКС на основе Si
модель	РЭЯ-Н		РЭЯ	-ЦГУ
дефект	в ЗЗС	в ЗВС	в ЗЗС	в ЗВС
В	49,69	59,89	35,69	50,69
AI	2,20	80,10	3,08	63,04
Ga	35,54	80,61	24,40	63,26
F	23,74	77,91	20,14	70,92
Cl	42,95	32,93	32,28	25,78
ДКС на основе Ge
модель	РЭЯ-Н		РЭЯ	-ЦГУ
дефект	в ЗЗС	в ЗВС	в ЗЗС	в ЗВС
В	70,23	52,48	59,27	85,39
AI	50,19	60,31	73,60	89,83
Ga	70,80	62,02	74,16	90,45
F	25,19	41,98	36,29	44,33
Cl	49,81	3,24	65,84	7.87

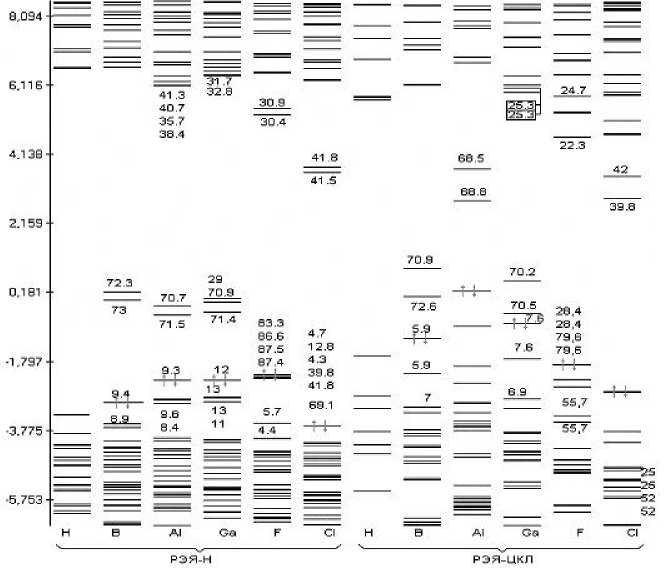
Рис. 5. Спектр одноэлектронных состояний ДСК с гидридным покровом на основе алмаза бездефектной (Н) и с локальными дефектами замещения поверхностной группы С-Н на атомы В, Al, Ga и атома Н на F, Cl (по результатам расчета моделей РЭЯ-Н и РЭЯ-ЦКЛ)

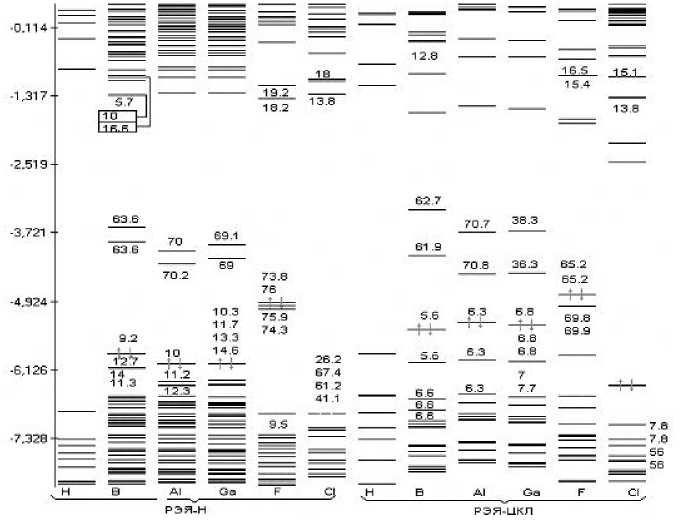
Рис. 6. Спектр одноэлектронных состояний ДСК с гидридным покровом на основе кремния бездефектной (Н) и с локальными дефектами замещения поверхностной группы С-Н на атомы В, Al, Ga и атома Н на F, Cl (по результатам расчета моделей РЭЯ-Н и РЭЯ-ЦКЛ)

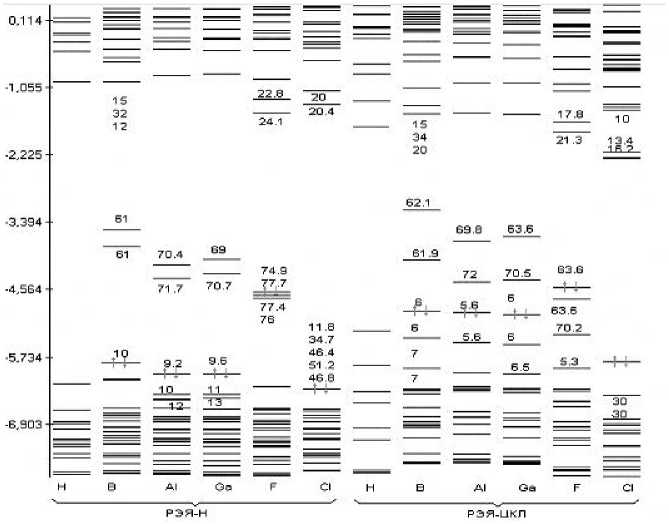
Рис. 7. Спектр одноэлектронных состояний ДСК с гидридным покровом на основе германия бездефектной (Н) и с локальными дефектами замещения поверхностной группы С-Н на атомы В, Al, Ga и атома Н на F, Cl (по результатам расчета моделей РЭЯ-Н и РЭЯ-ЦКЛ)

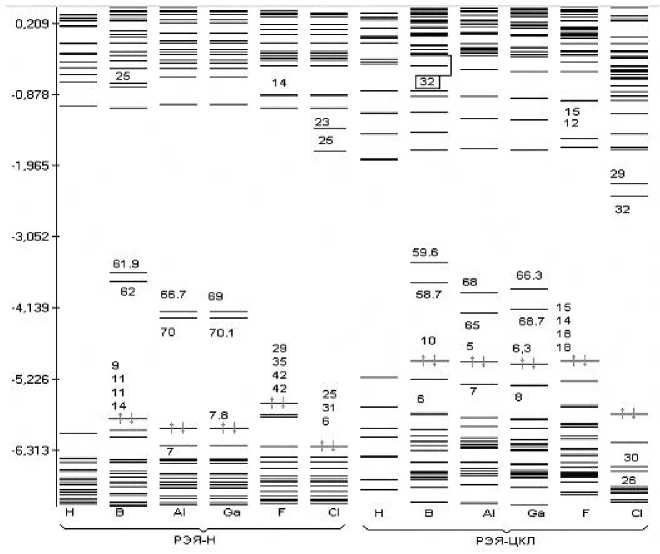
Рис. 8. Спектр одноэлектронных состояний ДСК с гидридным покровом на основе германия бездефектной (Н) и с локальными дефектами замещения поверхностной группы С-Н на атомы В, Al, Ga и атома Н на F, Cl (по результатам расчета моделей РЭЯ-Н и РЭЯ-ЦКЛ) (3 х 3 х 4 )

Список литературы Электронное строение и энергетический спектр двумерных ковалентных структур с локальными дефектами

Hohenberg P., Kohn W. Inhomogeneous Electron//Gas Phys. Rev. 1964. V. 136. P. B864.
Kohn W., Sham L.J. Self-Consistent Equations Including Exchange and Correlation Effects//Phys. Rev. 1965. V 140. P. A1133.
Hehre W.J., Stewart R.F., Pople J.A. Self-Consistent Molecular-Orbital Methods. I. Use of Gaussian Expansions of Slater-Type Atomic Orbitals//J. Chem. Phys. 1969. V 51. P. 2657.
Perdew J.P., Burke K., Ernzerhof M. Generalized Gradient Approximation Made Simple//Phys. Rev. Lett. 1996. V 77. P. 3865.
Perdew J.P., Burke K., Ernzerhof M. Generalized Gradient Approximation Made Simple//Phys. Rev. Lett. 1997. V 78. P. 1396.
M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J. R. Cheeseman, V.G. Zakrzewski, J.A. Montgomery Jr., R.E. Stratmann, J.C. Burant, S. Dapprich, J.M. Millam, A.D. Daniels, K.N. Kudin, M.C. Strain, Ö. Farkas, J. Tomasi, V. Barone, M. Head-Gordon, E.S. Replogle and J.A. Pople. См.: Программа Gaussian-98 (Gaussian, Inc., Pittsburgh, PA, 1998).

Статья научная