Элементарная сеть, ассоциированная с элементарной группой

Пусть R — произвольное коммутативное кольцо с единицей, n — натуральное число, n >  3. Снетома ст = (CT ij ). 1 6 i, j 6 n, аддитивных подгрупп кольца R называется сетъю [1] над кольцом R порядка n, если CT ir CT rj С CT ij при всех значениях индексов i, r, j. Для сети принята также терминология «ковер» [2]. Сеть, рассматриваемая без диагонали, называется элементарной сетью ^элементарный ковер [3, 4, вопрос 15.46]). Для элементарной сети в [5] введено понятие производной элементарной сети.

Пусть e — единичная матрица порядка n. e ij — матрипа, у котюрой на позиции ( i, j ) стоит 1, а на остальных местах нули. Если а Е R, то через t ij ( а ) = e + «e ij обозначается элементарная трансвекция. Положим, далее, t ij ( A ) = {t ij ( а ) : а Е A}.

Для элементарной сети ст через Е(ст) обозначается элементарная сетевая группа:

E (ст) = (tij- (CT ij ) : 1 6 i= j 6 n\

Элементарная сеть ст = (CT ij ). 1 6 i = j 6 n называется пополняемой. если для неко торых аддитивных подгрупп CT ii кольца R таблица (с диагональю) ст = (CTij), 1 6 i, j 6 n, является (полной) сетью. Элементарная сеть ст = ( CT ij) является дополняемой (см., на пример, [1]) тогда и только тогда, когда CT ij CT ji CT ij С CT ij для любых i = j .

В [6] определены замкнутые (допустимые) сети. Для элементарной сети ст рассмотрим элементарную сеть CT = ( CTij), индуцированную трансвекциями из элементарной группы E ( ст). Точнее, посмотрим, какие элементарные трансвекции появились (содержатся) в E ( ст). А именно, для любых i = j положим

CTij = {а Е R : t ij (а) Е Е(ст)}.

Очевидно, что CT ij — аддитивные группы и в силу известного коммутаторного соотношения (для попарно различных i, r, j)

[tir (а),trj (в)] = t ij (ав )

мы имеем CTirCT_rj С CTij, а потому таблица CT = (CTij)_i=_j является элементарной сетью.

ОПРЕДЕЛЕНИЕ. Элементарную сеть о мы называем за мыканием сети ст. Если ст = ст, то сеть о мы называем замкнутой (или допустимой).

Предложение 1. Всякая дополняемая элементарная сеть является замкнутой.

C Пусть о = (o ij ) — дополняемая элементарная сеть (и мы дополнили ее диагональю до (полной) сети). В этом случае в силу сетевого соотношения O ir o rj С o ij (выполненное для всех 1 6 i,r,j 6 n) множество матриц

M(о) = {a = (aj) : aj Е oj, 1 6 i, j 6 n} является кольцом, следовательно, e+M(о) — полугруппа, в частности, E(о) С (e+M(ст)), а потому никаких новых элементарных трансвекций в E(о) быть не может: если а Е orj, т. е. tij(а) Е Е(о). то tij(а) Е (e + M(о)) ^ aeij Е M(о) ^ а Е oij ^ о = ст. B

С другой стороны в [6] приводятся примеры замкнутых сетей, которые не являются дополняемыми. Интерес к дополняемым сетям состоит в том, что по таким сетям строятся сетевые группы [1].

Пусть а. в подгруппы аддитивной группы кольца R. Для элементарной сети т второго порядка т=

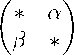
положим y = Р&=1(ав)k• Рассмотрим элементарную группу E(т ) = (t2i(в)Д12 (а)).

1 + ail ai2

Можно показать, что если а Е Е(т), a =           .        , то ац, а»» Е y, ai2 Е а + aY, a21    1 + a22

а»1 Е в + eY. Последнее замечание индуцирует следующее построение.

Для любых i = j положим

∞

^Y ij = X ^(o ji ^o ij ^)m.

m =1

Для произвольных i = j поло жим ^ ij = o ij + o ij Y ij •

Предложение 2 [5, предложение 5]. Таблица П = (Qj), 1 6 i = j 6 n, является дополняемой элементарной сетью.

С другой стороны в [5] для элементарной сети определяется производная элементарная сеть. А именно, Пусть о = (o ij ) — элементарная сеть над кольцом R порядка n. Рассмотрим набор ш = (ш ^ ) аддитивных подгрупп w ij кольца R, определенных для любых i = j следующим образом:

n

ω ij

^σ ik ^σ kj ^, k =1

где, очевидно (так как о — элементарная сеть), суммирование берется по всем k, отличным от i и j. Ясно, что Ш ij С o ij, следовательно, для любой тройки попарно различных чисел i. r. j, мы имеем

ωir ωrj ⊆ ωij ^.

Таким образом, набор ш = (шij ) аддитивных подгрупп Шij, i = j, кольца R является элементарной сетью, которую мы называем производной элементарной сетью.

Предложение 3. Для любой тройки попарно различных индексов г, r, j справедливы включения nir nrj С шij,   nir шrj С шij,   шir nrj С шij.

Элементарная сеть, ассоциированная с элементарной группой

C Заметим, что второе и третье вк.ткннтшя вытекают из первого и того, что w rj С П ^. W ir С П i_r. Поэтому докажем первое.

Пусть i, r, j — попарно различные натуральные числа. Заметим вначале, что

O ir ^O jr ^o rj ) ^{С o} ir ,    ^o rj ^(o ir O ri ) ^{С o} rj .

Поэтому

(O ir + O ir (O ir O ri ) k )(O rj + O rj (O jr O rj ) s )

= ° ir ° rj ⁺ ° ir ° rj ⁽° jr ° rj ) ^{+ (o} ir ° rj ^)(o ir ^o ri ) ^(o jr ^o rj ) ^{+ (o}ir ^o rj ^)(o ir ^o ri )

= O ir O rj + [O ir (O rj O jr ) s ] O rj + [O ir (O rj O jr ) s ][( o ri O ir ) k O rj ] + O ir [(O ri O ir ) k O rj ] С O_ir O_r j С W ij . >

Как нетрудно видеть, элементарную сеть П = (П^), 1 6 i = j 6 n, можно дополнить до сети кольцами

Пп = ^2^ ik П

i ^,

k 6= i

где суммирование берется по к = 1, 2,... , n, к = г. Заметим, что n

Пи = £ Y ik .

k=1, k6=i

Так. например. П_и = Y 12 + Y 13 + • • • + Y in .

ОПРЕДЕЛЕНИЕ. Сеть П = (П^) мы называем сетью, ассоциированной с элементарной группой E(o) для элемептарной сети o.

Ясно, что o С П.

Теорема. Сеть П является наименьшей (дополняемой) сетью, содержащей элемен тарную сеть o.

C Пусть т — дополняемая сеть ho С т. Покажем, что П С т. Сначала покажем, что для i = j. П ^ С T ij. Напомиим. что (i = j)

^П ij — ^o ij ^{+ o} ij ^(o ji ^o ij ) ^{+ o} ij ^(o ji ^o ij ) ⁺ . . .

Имеем O ij С T ij. далее, в силу дополияемоети сети т mbi имеем T ij T ji T ij С T ij. а потому

Oij (ojioij ) С тijтjiтij С тij, из последнего включения мы имеем

^O ij ^(o ji ^o ij )  ^{С т} ij ^(o ji ^o ij ) ^{С т} ij ^т ji ^т ij ^{С т} ij ^.

и так далее. Следовательно, для i = j мы имеем П ij С T ij. Далее, в силу того, что мы стандартным образом (т. е. наименьшей диагональю, определенной через недиагональные элементы сети П, которые, как мы уже доказали, не больше соответствующих элементов сети т) дополнили элемептарпую сеть П диагональю, мы имеем Пц С тп- B