Элементарные теплофизические модели трения

чатых материалов при внешнем трении, обобщение которых представлено в работах [3, 4]. В настоящей статье приведены основные результаты этих исследований применительно к трению только инертных тел.

Элементарные теплофизические модели трения представлены на рис. 1. При проведении расчетов трущиеся тела принимаются гомогенными, а их теплофизические характеристики постоянными. Считается, что работа сил трения полностью переходит в тепло. Сила трения принимается зависящей только от температуры на поверхности трения, причем зависящей по степенному закону ттр (T) - гтр

n

• 1-    T^T O- Т *“М

  
  

где Гтр - удельная сила трения, T - температура на поверхности трения, г^р - удельная сила трения при начальной температуре T0, n и T* - некоторые параметры, подбираемые из условия наилучшей аппроксимации формулой (1) действительной зависимости Гтр (T). При сравнительно небольших давлениях прижатия трущихся тел p величина f =f -р , где f коэффициент трения, а при очень больших давлениях!тр =Тпр , где Тпр - предел прочности на сдвиг менее прочного из трущихся тел.

В первом приближении за величину T* можно принимать температуру плавления Тпл наиболее легкоплавкого из трущихся тел. При n = 1 зависимость (1) становится линейной. В первых трех моделях рассматривается разогрев инертных твердых тел при сухом кратковременном трении, когда на поверхности трения не достигаются температуры, близкие к Tпл, и не образуется текучая пластическая прослойка. Толщина каждого из трущихся тел больше соот- ветствующей толщины зоны прогрева тела у поверхности трения:

h> ^1,73 jai t mp , (2) где a i – температуропроводность материала тела, i = 1 или 2 – номера трущихся тел в моделях рис. 1, t тр – время (продолжительность) трения. В этом случае трущиеся тела можно моделировать в тепловых задачах полупространствами.

1. Первая расчетная модель (рис._1) – одномерная модель сплошного фрикционного контакта реализуется либо при больших давлениях прижатия трущихся тел, когда площадь фактического касания составляет значительную часть номинальной площади фрикционного контакта, либо при больших временах трения, когда температура всех участков поверхности трения становится близкой к температуре пятен фактического касания. Температуру на поверхности трения в этом случае называют средней поверхностной температурой. На поверхности трения происходит тепловыделение трения с удельной мощностью q = т V . где V — скорость скольжения.

где λ i   коэффициенты теплопроводности; с i –

удельные теплоемкости; ρ i – плотность материалов

трущихся тел, а также выражение для температуры на поверхности сухого трения в виде формулы Дюамеля

t

T = T o+ ,   ’     - f q i( t - Cd d =.⁽⁵⁾

1c X_x C1P1 0         V<

где t – время, а зависимость q 1 ( t ) определяется функциями изменения во времени скорости V(t) и давления прижатия p(t) . В случае постоянной мощ-

ности тепловыделения const,                    const q тр            q1         тп q тр из формулы (5) получается формула для нахождения средней поверхностной температуры на поверхно-

сти сухого трения:

T

= To +

2 q1 ^

4я 1с1\С1РХ

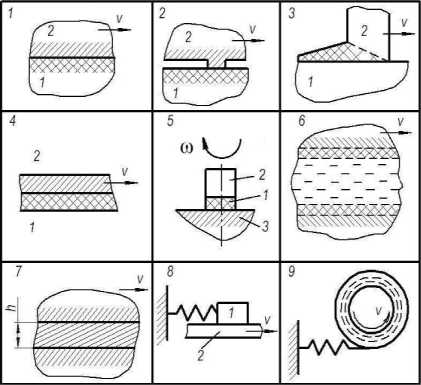
Рис. 1. Теплофизические модели трения.

Эта формула может применяться для расчета не очень больших разогревов.

При учете линейной зависимости силы трения от температуры (1) для n =1 и постоянных скорости скольжения и давлении прижатия, граничное условие на поверхности трущегося тела можно записать

в виде граничного условия третьего рода q1 = TmjT(T — T). ^тр = (1 — ^тп )TmpV /(T “T0). (7)

где коэффициент a_mp^

связывающий параметры

трения и теплофизические свойства пары трения, является фрикционным аналогом коэффициента теплообмена в законе теплообмена Ньютона, что впервые было замечено в работе [5]. Это позволяет для расчета средней поверхностной температуры

трения использовать хорошо известное в теории

теплопроводности решение задачи для граничного

условия третьего рода

T = T-(^-ОГ^ф ^тр

t

А ^С1Р1

Выделяющееся тепло разделяется на два тепло-

где

вых потока, идущих на нагрев трущихся тел: q тр =q1+q 2или q 1(1-am) q тр. q 2= ^тп q тр. (3) где – коэффициент распределения тепловых потоков, представляющих собой долю тепла трения, которая поступает в тело 2. Из решения контактной задачи о нагреве двух полубесконечных трущихся тел получается формула Шаррона для коэффициен-

2 W                   .^2

Ф(w ) = exp( w ²)(1—fexp(- u ²) du ) = e  <-erf( w)

-^TT 0

– специальная функция, связанная с функцией ошибок Гаусса erf (w) . При расчете по формуле (8) рост

та распределения тепловых потоков

7^ 2 с с2Р 2

™   i1c1l^c1PX + 7^2 ^c 2P2

температуры при сухом трении ограничен температурой T , что соответствует теплофизике трения, чем по формуле (6).

Если перейти к относительной, безразмерной температуре ^ = ( T - T o ) /( Г - T o ). то формулы (6) и (8) запишутся в виде

3 =(2/ Vtt) Bi mp , S=M( Bi mp ), (9)

где iтр

тр a l t _ ⁽¹   ^тп ) ^тр ^V^t    (10)

A      ( T ~ ^To)^1^c1P1

фрикционный аналог критерия Био.

Из формул (9) видно, что критерий Bi тр определяет относительный разогрев поверхности трения. При малых значениях ( Bi тр <<1) мал и относительный разогрев поверхности (О «1). При увеличении Bi тр и приближении его к единице фрикционный разогрев становится значительным. При больших значениях ( Bi тр >>1) относительный разогрев приближается к 1, а размерная температура на поверхности трения приближается к значению

T . Таким образом, фрикционный аналог критерия (10) является единственным безразмерным комплексом величин, который включает в себя все необходимые свойства трущихся тел и параметры кратковременного сухого трения при сплошном фрикци- онном контакте и однозначно определяет среднюю поверхностную температуру трения в модели 1. По физическому смыслу фрикционный аналог критерия Био характеризует отношение интенсивности тепловыделения трения к интенсивности отвода тепла в глубь трущихся тел путем теплопроводности. При больших значениях этого критерия (Biтр>>1) велик и фрикционный разогрев на поверхности трущихся тел, а при малых значениях (Biтр<<1) фрикционный разогрев мал. Таким образом, вычислив величину критерия Biтр, без всяких других вычислений, можно судить о степени фрикционного разогрева. Понятие о фрикционном аналоге критерия Био является фундаментальным для теплофизики трения (аналогично критерию Био для теории теплопроводности), так как этот критерий остается главным критерием, определяющим фрикционный разогрев при сухом трении, при нелинейной зависимости силы трения от температуры и в других моделях сухого трения и трения со смазкой, например, для дискретного фрикционного контакта, трения, автоколебательном режиме и т.д.

• 2.    Модель 2, рис. 1 – двумерная модель дискретного фрикционного контакта. Реализуется при небольших давлениях прижатия. Рассматривается единичное пятно контакта жесткого и шероховатого тела 2 с более пластичным и гладким телом 1. Пятно контакта имеет простейшую геометрическую форму в виде круга диаметром d r или квадрата со стороной d r , или полосы шириной d r . На пятне контакта происходит тепловыделение трения с удельной мощностью q тр =ттр V A k / A r , где Т_тр - удельная сила трения на номинальном контакте; А к , А r – соответственно номинальная и фактическая площади фрикционного контакта тел 1 и 2. Стационарный (установившийся) разогрев тел 1 и 2 поверхностными источниками с постоянной мощностью теплово-

• го потока q1 и q2 описывается известными решения-
• ми Блока и Егера. Дополняя решения Блока и Егера (11), (12) численным решением задачи о нагреве тела 1 быстро движущимся Pe Vd. / a<>20, по-
• лосовым источником тепла с мощностью теплового потока q1, зависящей степенным образом вида (1)

от температуры на поверхности, и приравнивая максимальные температуры тел 1 и 2 на пятне контакта, получим следующие выражения для определения максимальной температуры Tm на пятне контакта при учете зависимости (1) силы трения от темпера- туры:

т™_ __{1 = 0},   ,9 _ ^Tm-T 0 (11)

Bi тр               ^T* “ ⁷ 0

где фрикционный аналог критерия Био

_ атр / a i dr _ « — т _тп ) Tmp VA k I   d f_r      (12)

Biwin                                                      , mp ^ \ 2V    (T-To)Ar  pVIcQA а коэффициент распределения тепловых потоков атп = <+(л/^/4)(21/22) T^ef^1. (13)

Таким образом, и в модели 2 фрикционный аналог критерия Био является главным критерием, определяющим фрикционный разогрев на пятно каса- ния трущихся тел.

• 3.    Модель 3, рис. 1 представляет собой модель разогрева при сухом трении с износом. Тело 2 в виде полуограниченного прямого кругового цилиндра диаметром D , либо в виде полуограниченной плоской пластины толщиной D скользит с постоянной скоростью V по поверхности полубесконечного тела 1 и перемещается к нему вследствие износа со скоростью v I V , где I 2 – безразмерная интенсивность изнашивания тела 2. С боковой поверхности тела 2 происходит теплоотвод в окружающую среду с коэффициентом теплоотдачи α, а поверхность тела 1 вне контакта адиабатическая. Температура окружающей среды принята равной начальной температуре тел T 0 . Определяется максимальная стационарная температура T m на фрикционном контакте, обусловленная       тепловыделением       трения

Ч тр = Тр^ ™ q < + q 2 . Максимальный стационарный разогрев тела 1 при быстром движении ( Pe < vDD / a <>20) определяется формулой Егера (12),     которая     здесь     примет     вид

7 1- T , = (2/V^)( q , D /(X , V Pe ij).

Для максимального разогрева тела 2 получена формула ⁷ 2 - T o = q 2^/( (^c2P2°2 ),        ⁽¹⁶⁾

где безразмерный параметр ζ характеризует интенсивность теплопотерь через боковую поверхность тела 2 (при отсутствии теплопотерь ζ=1), П/S – отношение периметра к площади сечения тела 2 (П/S=2/D – для пластины, П/S=4/D – для круглого стержня). Рассмотрено три вида модели 3[8]. Первый вид – с равномерно нагретым слоем износа, когда в зоне контакта тел одинакова температура частиц износа и поверхностей трущихся тел в точках, лежащих на одной нормали к поверхности трения. Здесь T1=T2=Tm и безразмерный максимальный фрикционный разогрев

8m = (2/V^)Biтр /(1 + ^ +^2), гДе 8m =THLT0^, ^2 Sc2/Ei m              22

!*-! 0         1TT\/.\C\P\

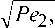
Bi.,--P^-D^, тр  (Т-Т0)Л V V

Pe 1 = VD / a 1 ,  Pe ₂ = VD / a ₂,

К 1=2114Pejit.(17)

Второй вид модели 3 – с поверхностным тепловыделением на границе слоя износа с телом 2, когда частицы износа тела 2 прилипают к поверхности тела 1, так что поверхность скольжения фактически перемещается внутрь изнашиваемого тела 2 на величину средней толщины слоя износа h2=I2D. Здесь T2 тТт, T2 — T1 = q1 h2 / X2 (слой износа тон- кий), и

2Bi- (1 + <52/2 + £2) тр m V^(1 + ^2+^2+^2/2)

4tt  1 c c i P\ ,  r^—        ne)

8 2 =-----. ----¹---- ¹ 2 ^^Pe 2 .        ⁽¹⁸⁾

² М2 c 2P2

Третий вид модели 3 – с объемным тепловыделением в пластическом слое износа, обладающем свойствами идеально пластического тела с пределом текучести на сдвиг τ т . (Можно принять τ тр = τ т ). При тонком слое износа (δ 2 <<1)

2 Bimp (1 + ^2)(1 + 2^2 + ^2 + 8 2 + 2e₂sp  ⁽ 19)

m                                                          •

-fir (1 + 2^^2)²

• 4.    Модели 4 и 5, рис. 1 предназначены для опре-

• деления разогрева твердых тел при сухом длительном трении, когда время трения намного превышает времена прогрева трущихся тел, условие (2) не выполняется, поэтому необходимо учитывать размеры трущихся тел hi в направлении распространения тепла и тепловые условия на их поверхностях. Сначала рассматривается вспомогательная задача о стационарном нагреве прямого цилиндра торцовым тепловым потоком. Прямой цилиндр выбирается высотой h c произвольной формой основания площадью S и периметром П. Продольная ось координат x направляется параллельно образующей цилиндра, а ее начало помещается на торец (основание) цилиндра, на котором действует равномерно распределенный тепловой поток q. На другом торце цилиндра и его боковой поверхности задается закон теплообмена Ньютона со средой, имеющей температуру T0, коэффициенты теплоотдачи Т для торца и Б для боковой поверхности. Трехмерная задача

теплопроводности решена с усреднением по поперечным координатам y и z методом С.И. Худяева с использованием первого собственного значения Cj2 соответствующей краевой задачи теплопроводности. Решение задачи о распределении температуры по оси x в цилиндре имеет следующий безразмерный вид:

A е B е , (20)

А =        (^-Bi ^Т )е ^-2<

С «(1-е " ²^) + Bi ^Т (1 + е '^О/

В =                    Bi ^т              , (21)

< «(1-е - ²<) + Bi ^т (1 + е-²<)) где безразмерные переменные и параметры

У = Л ( Т-Т ₀)/( qh ),£ xx / h ,

т)- T     Ту d-Б     Б z   ^Oh

Bi -a h , Bi -а то, Z = ——, (22) ^r 0

r 0 – характерный линейный размер основания. Для кругового цилиндра радиусом r 0

а о —> 7t /2 при Bi Б —> oo, c0 -> 42BiБ при BiБ -> 0.(23) Для цилиндра в виде неограниченной пластины толщины l ст о -> к / 2 при BiБ -> oo, сто -> V BiБ при BiБ -> 0 , (24) при этом т -i/2, если на обеих боковых поверхностях пластины задан один и тот же коэффициент ББ ф 0, или Tq = l, если на одной боковой поверхности ББ = 0, а на другой бб ф 0.

В модели 4 рассматривается длительное трение двух тел при поступательном движении. Тело 1 нагревается тепловым потоком q1, а тело 2 – потоком q2, причем q1+q2=qтр=τтр·V. Характеристики двух трущихся тел в виде прямых цилиндров с высотами h1 и h2 обозначается соответственно индексами 1 и 2. Стационарный нагрев каждого тела описывается формулами (23) – (25), в которых следует использовать величины, относящиеся к рассматриваемому телу 1 или 2. Приравнивая температуры тел на плоскости трения x=0, получим следующее выражение для коэффициента распределения тепловых при длительном сухом трении а тп = q2 / qmp тп

Q ₊ 1 h^h 2⁽ A 2 ^+В 2) А-1

7 2 ^h 1⁽ A 1 + ^B 1 )

которое принципиально отличается от формулы Шаррона (4) для кратковременного сухого трения.

• 5.    В модели 5 рассматривается длительное трение вращения. Тело 1 в виде сплошного прямого кругового цилиндра диаметром D и высотой h 1 находится на полубесконечном основании (тело 3) и подвергается воздействию трением вращающимся прямым цилиндрическим пуансоном высотой h 2 (тело 2). Усредненная мощность фрикционного тепловыделения на круговом контакте тел 1 и 2

• 6.    Модель 6 предназначена для описания процесса образования пластической и жидкой прослоек при фрикционном разогреве твердых тел. Эта модель на заключительной стадии процесса представлена на рис. 1, где в середине изображена жидкая прослойка, перекрестной штриховой обозначены пластические прослойки, а косой штриховкой – твердые части трущихся тел. В качестве пары трения приняты два одинаковых полубесконечных тела, скользящих поступательно относительно друг друга со скоростью V и имеющих вследствие рассматриваемых высоких температур сплошную плоскость фрикционного контакта. Рассмотрено постадийное развитие процесса. Первая стадия – стадия сухого трения, исследованная при рассмотрении модели 1. Вторая – стадия образования при температуре T т и развития жесткопластической прослойки между трущимися телами. Третья – стадия образования при температуре плавления T пл жидкой прослойки и совместного течения ее вместе с пластической прослойкой. Четвертая и пятая – стадии течения только жидкой прослойки, когда напряжение сдвига жидкой фазы становится меньше минимального значения предела текучести пластической прослойки. Задача о развитии прослоек на каждой стадии решена с использованием приближенных методов интегральных соотношений (аналогично В.Б. Либровичу) и усреднения (по С.И. Худяеву), в результате чего сведена к системам обыкновенных дифференциальных уравнений, которые легко решаются на ЭВМ с использованием стандартных методов решения [9].

qтр — 7"тр (Т) COD /3,  qmp — q1 + q2, где ω – угловая скорость вращения пуансона. Тепловые потоки q1 и q2 направлены в тела 1 и 2 от плоскости трения, а тепловой поток q3 из тела 1 в тело 3. Используя формулу Блока (11) для нагрева полубесконечного тела 3 круговым неподвижным источником с мощностью q3, можно написать q3=(2^/D)Т-To) = «mТ-То), (26) что эквивалентно закону теплообмена Ньютона для нижнего торца цилиндра 1 со средой температуры Т0 при коэффициенте теплообмена ос т =223/ D.               (27)

В итоге задача о разогреве твердого тела 1 при трении вращения сводится к рассмотренной выше задаче о разогреве тел 1 и 2 при поступательном движении, когда на торце тела 1 x=h 1 задается условие теплоотдачи (26).

Получены формулы для предельно возможных значений усредненной по толщине жидкой прослойки и максимальной величин фрикционного разогрева:

_тпр „  _(^(^ )V ²            _К Тр Р )V ² (28)

T ср ^Т пл         о       , ^Т макс ^Т пл      ~ а     ^.

тт ²Л_Ж                    2Л Лк

ж где ц(Тпр) —значение динамической вязкости жидкой фазы при усредненной температуре T пр , коэффициент теплопроводности жидкой фазы. В безразмерном виде эти формулы запишутся так:

9 Тр =Bi ^ _pV Т р )/^Т ,_а ),

9 МРакс =(ч/2) ВЖ (ТСРР )/ц(Т„ ), где        „,ж=   Н (Т„ )V2

BiTP   m-21’

^  ж (Тпл пр                T пр T пр     Tмакс   Tпл    пр    ср     пл (30)

макс      гр     гр , ср     гр     гр

Т пл Т0              Т пл Т0

Сравнение формул (10) и (30) показывает, как изменяется вид фрикционного аналога критерия Био при переходе от сухого трения к трению при наличии жидкой прослойки, но сохраняется физический смысл этого критерия, характеризующего отношение интенсивности тепловыделения трения к интенсивности отвода тепла в глубь трущихся тел.

• 7.    В модели 7, рис. 1, рассматривается кратковременный фрикционный разогрев твердых тел при наличии между ними прослойки сдвига с равномерной толщиной h , не меняющейся в ходе сдвига. В прослойке скорость сдвига непрерывно падает от значения V до нуля, причем профиль скорости является прямолинейным. За счет внутреннего трения в прослойке происходит объемное фрикционное тепловыделение     с     удельной     мощностью

q v = трр¥ /h. На начальной стадии теплоотвод в прилегающие полупространства еще не будет сказываться на нагреве центральной части прослойки, поэтому первую стадию разогрева прослойки можно назвать адиабатической. Изменение температуры T прослойки во времени t при адиабатическом нагреве за счет внутреннего трения:

Т-Т о = q_vt /(cp) = T _mvV/ /(cph ).    (31)

При больших временах уже большая часть выделяющегося в прослойке с мощностью q h тепла будет уходить из прослойки в прилегающие к ней холодные полупространства трущихся тел в виде тепловых потоков q — q_vh /2.

Нагрев поверхности полупространства под действием постоянного теплового потока q описывается формулой (6), которая для рассматриваемого случая примет вид

Т п = Т о +(2/7^) q,1 (/-/ н )/( Лер ), (32) где t н – момент начала действия постоянного теплового потока q .

Если практически все тепло уходит из прослойки в прилегающие тела, то в прослойке установится стационарный профиль температуры

T ( x , t ) -T_n = ( qvh² /(8Я))(1-4 x² Ih 2)(33) который будет медленно изменяться во времени (квазистационарно) с изменением температуры поверхностей прослойки T п .

• 8.    Модель 8 (для сухого трения) и модель 9 (для трения со смазкой), рис. 1, привлекаются для исследования влияния наличия упругих связей в системе трения на фрикционный разогрев и возникновение автоколебаний, которые называются также механическими релаксационными колебаниями или скачками при трении. В автоколебательном режиме трение представляет собой не равномерное относительное скольжение фрикционных элементов со скоростью V заданного равномерного перемещения одного из элементов, а состоит из последовательного чередования двух различных этапов: этапа относительного покоя фрикционных элементов и этапа скачка – неравномерного относительного скольжения их. Скорость скольжения при скачке может достигать значительных величин и намного превышать величину V. В зависимости от относительной длительности этапов график колебательного процесса может быть либо близким к синусоидальному, либо пилообразным. Во время этапа относительного покоя происходит накопление потенциальной упругой энергии в системе, во время этапа скачка происходит самопроизвольная упругая разгрузка с переходом запасенной упругой энергии в работу сил трения. Для того чтобы упругая разгрузка была возможной, необходимо, чтобы сила трения скольжения была меньше силы трения покоя в момент срыва. Это условие может быть выполнено в силу самых разных причин. Тепловая теория объясняет возникновение автоколебаний при внешнем трении зависимостью силы трения от температуры [6, 7]. Согласно этой теории, во время скачка происходит фрикционный нагрев поверхности трения, вызывающий уменьшение силы трения скольжения по сравнению с силой трения покоя, что и приводит к самопроизвольной упругой разгрузке, т. е. к автоколебаниям.

Модель 8 используется для построения тепловой теории автоколебаний при сухом трении. Один элемент пары трения связан с абсолютно жесткой механической системой, другой – с линейной колебательной системой с одной степенью свободы. Запи- сываются уравнения движения и теплопроводности, которые приводятся к безразмерному виду. Основ-0

ные безразмерные критерии: £ =--- тр

V  k1m1

Ri

Biтр

⁽¹   ^тп )

(т Тр )²       и.

k . C T-T op С1Р1’

где к 1 и m 1 – соответственно жесткость пружины и масса тела 1, приходящиеся на единицу площади поверхности контакта трущихся тел,

CO} = ^ к I m^ - частота свободных колебаний. Характерные величины у0 = т 0Пр IК — координата первого срыва (скачка), v y скорость скачка, tK= Ш^1 — время скачка. Величина критерия ε характеризует степень нелинейности колебательной системы. При больших e(s »1) колебательная система сильно нелинейна, автоколебания носят релаксационный характер. При малых 8(е «1) колебательная система слабо нелинейна, колебания здесь являются квазигармоническими. График движений тела 1 близок к синусоидальному. Фрикционный аналог критерия Био Biтр – главный критерий, ответственный за возникновение автоколебаний. По физическому смыслу критерий Biтр характеризует отношение времени тепловой релаксации тепловыделения трения при колебании к характерному времени колебаний. Существует критическое значение критерия Bi кр = 1,74. При

Bi тр > Bi^кр сухое трение сопровождается возникновением автоколебаний тепловой природы.

• 9.    Модель 9, рис. 1, используется для построения тепловой теории автоколебаний при трении со смазкой. Система трения представляет собой две недеформируемых бесконечных круглых соосных трубы, разделенных слоем смазки толщиной h . Внутренняя труба равномерно вращается, линейная скорость вращения на границе трубы со смазкой равна постоянной величине V . Внешняя труба посредством упругого элемента связана с неподвижной абсолютно жесткой системой и образует упругую систему. Через m 1 и k 1 обозначается соответственно масса и жесткость упругой системы, приходящиеся на единицу площади поверхности трения. Температура смазки T принимается равномерно распределенной по всему объему смазки. Температура ограничивающих поверхностей считается постоянной в ходе процесса трения и равной начальной температуре смазки T 0 . Рассматривается смазка вязкопластического типа:

т(T) = Ho(do I dr). f (T) + Tog(T),   (35)

где     касательное напряжение в смазке, d /dr – скорость деформации смазки, То и ц0 - соответственно предельное напряжение сдвига и динамическая вязкость смазки при начальной температуре T0 (в частных случаях То =0 или Цд = 0), f (T) и g(T) - монотонно убывающие функции, описывающие зависимость реологических характеристик смазки от температуры, причем

.f (To) = g (T,) = 1.

Данная система трения со смазкой описывается системой обыкновенных дифференциальных урав- нений движения и теплового баланса, качественное исследование которой на устойчивость по Ляпунову позволяет определить в общем виде условия возникновения автоколебаний (условие Гурвица неустойчивости положения равновесия системы):

A + ( A + D)(AD-BC) <0      (36)

где коэффициенты

A  '-■;:! (.9*), B = s< f '^}- vg G9*)),

C = Bimp (2 f (,9*) + vg(S*))/<5, D = (1 + Bimp B) / 3

В точке равновесия системы

£ = 0, T] = f <9 ) + vg(9 ), Bi mp ( f (.9*) + vg (S*)) = S*.

Здесь использованы безразмерные переменные и параметры:

t[A.-d .

} m1     V]m1     dTT cphk

2a \ mi '

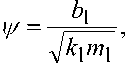
^ 0 h   P =

,, v0 v     Mki mi

Bi mp = ^ 0 ^{V 2}

2 ah- м "

Размерные переменные и параметры: t – время, y – смещение внешней трубы от равновесия,

ОС = л² x / 2 h —коэффициент теплоотдачи из смазки в стенки труб, T м – масштаб температуры.