Элементы гармонизации в архитектуре памятника Кой-Крылган-Кала

Известный хорезмский памятник Кой-Крылган-кала (IV в. до н. э. – IV в. н. э.) относится к редкому типу сооружений, в основе которых находится правильная круговая форма. На всей территории Хорезма кроме самой Кой-Крыл-ган-калы форму круга имеют Чильпик, Дэу-кала, круглые храмы в комплексе сооружений Калалы-гыр 2 и Гяур-3, крепость Топрак-кала Шаватская в Южном Хорезме. Если же в процессе классификации ориентироваться не только на круглую форму сооружения, но и на другие архитектурные особенности объекта, то Кой-Крылган-кала окажется уникальным сооружением.

Принято считать, что с точки зрения планиграфии типологическим прототипом Кой-Крылган-калы является бактрийский круглый храм Дашлы-3. Оба сооружения имеют форму кольца, укрепленного по окружности девятью башнями. Исследователи относят эти сооружения к классу культовых или дворцово-культовых, что является дополнительным фактором, подчеркивающим их сходство. Однако сложность состоит в том, что памятники разделены и в пространстве, и во времени. Дашлы-3 датируется первой половиной II тыс. до н. э., Кой-Кры-лган-кала – IV–III вв. до н. э.1, при этом сами сооружения находятся более чем в 2000 км друг от друга. До настоящего времени в Центрально-Азиатском регионе не найдено памятников-аналогов, которые заполняли бы хронологический интервал от Дашлы-3 до Кой-Крылган-калы. Возможно, архитектурное сходство памятников и можно было бы рассматривать как аналогию, однако мы разделяем позицию, что прямое сопоставление каждого конкретного памятника РЖВ и античности с памятниками БМАК требует доказательства (Кошеленко, Гаибов, 2013. С. 199, 200).

Известно, что «сабейские»² храмы Первопричины, Первого разума, Миропорядка (Гармонии), Необходимости и Души были круговой формы ( Shahrastani , 1993. Р. 171, 172; Булатов , 1978. С. 16, 17). Храмы Солнца, Луны и планет имели форму различных геометрических фигур, в основе которых находилась фигура выпуклого многоугольника. В частности, Юпитеру соответствует треугольник; Меркурию – треугольник, содержащий прямоугольник; Венере – треугольник в квадрате; Марсу – прямоугольник; Солнцу – квадрат; Сатурну – шестиугольник; Луне – восьмиугольник. Наиболее вероятно, что в этой иерархии наибольший статус отводился храмам круговой формы, посвященным универсальным сущностям (законам) Вселенной. Эти сущности регламентировали законы космоса, которым подчинялись все небесные тела. Поэтому соответствующая им форма в основе многоугольника имела меньший статус по сравнению с круговой формой. Обратим внимание на параллель между представлениями «сабейцев» и строителями Кой-Крылган-калы. Уникальный культовый памятник хорезмской культуры Кой-Крылган-кала имеет форму круга, а в «сабейской» культуре круговая форма соответствовала наиболее статусным объектам. Это можно объяснить тем, что в основе древнехорез-мийской и сабейской архитектурной традиции находится единый культурный первоисточник.

Показательно одинаковым является число башен на Дашлы-3 и Кой-Кры-лган-кале. Количество башен Дашлы-3 трактовалось по-разному. М. Мамедов считает, что число башен соответствует девяти месяцам плодородия ( Мамедов , 2003. С. 60). М. С. Булатов высказал предположение, что башни символизируют союз девяти бактрийских племен ( Булатов , 1978. С. 31). При этом каждая из башен посвящена верховному божеству одного из племен. Обобщая эти предположения, можно заключить, что в их основе лежит числовая гармонизация, в которой количество башен является отражением космического, социального или сакрального мировоззрения общества. Принимая во внимание архитектурное сходство и предполагаемое предназначение обоих памятников, нельзя исключить концепцию числовой гармонизации и на Кой-Крылган-кале. Однако идея числовой гармонизации не является единственно возможной.

Некоторые вопросы фортификации

Башни любой крепости выполняют, прежде всего, оборонительную функцию. Если высота башни превышает высоту крепостной стены, то она позволяет вести обстрел позиции противника с большего расстояния. Но главное, что наличие башен позволяет вести фланговый перекрестный огонь, поэтому расстояние между ними не может быть произвольным. Слишком тесное расположение башен не дает дополнительного оборонительного преимущества и лишь усложняет конструкцию сооружения. С другой стороны, расстояние между башнями должно позволять вести прицельный огонь для обороны соседней башни, поэтому оно не может быть слишком большим. Следовательно, должен существовать некоторый оптимум.

Для оценки оптимального расстояния между башнями можно обратиться к археологическим планам крепостей кангюйского периода Базар-кала ( Толстов , 1948. С. 112. Рис. 47) и Кургашин-кала (Там же. С. 111. Рис. 46). Расстояние между башнями на Базар-кале составляет в среднем 30 м, на Кургашине – 32 м (для длинной стороны) и 40 м (для короткой). Таким образом, оптимум расстояния находится в диапазоне 30–40 м. Однако в основе этих памятников лежит форма прямоугольника. В случае круглой формы необходимо принимать во внимание кривизну, поскольку при определенных соотношениях между радиусом (или диаметром) круга, геометрическими размерами и количеством башен соседние башни могут не простреливаться.

Дашлы-3 представляет собой кольцо диаметром около 35 м, к которому с внешней стороны приставлено 9 башен, представляющих в сечении квадрат размерами 2 × 2 м ( Булатов , 1978. С. 30). М. С. Булатов утверждает, что из археологических данных следует: изначально на Дашлы-3 планировалось сделать 7 башен, но впоследствии их число было увеличено до 9 (рис. 1). Напомним, что М. С. Булатов объясняет увеличение количества башен присоединением к уже существовавшему союзу 7 племен двух других, а также считает, что каждой башне соответствует главное божество одного из племен.

Оптимальную конфигурацию башен Дашлы-3 можно оценить с помощью геометрических соображений. Как мы упоминали выше, для сооружения круглой формы должно выполняться соотношение между радиусом, размерами башен и их количеством. На рис. 1 изображена конфигурация, при которой соседние башни не простреливаются. Известными параметрами являются внешний радиус Дашлы-3 R = 17,5 м, геометрические размеры башни, которая представляет собой квадрат со стороной а = 2 м. Необходимо оценить число башен, при котором соседние башни не простреливаются. Для простоты будем считать, что стрелок находится в точке А (рис. 2).

Наша задача состоит в нахождении угла ∠ АОВ , который определяет количество башен при их равномерном распределении по окружности. Сторона АВ касается окружности в точке С , поэтому ZAСО = 90 ° , а катет ОС равен радиусу R = OC . То есть в равнобедренном треугольнике АОВ = ( ОА = ОВ = R + a ) отрезок ОС является высотой, медианой и биссектрисой, откуда ∠ АОВ = 2 ∠ АОС = α . Косинус половинного угла определяется соотношением

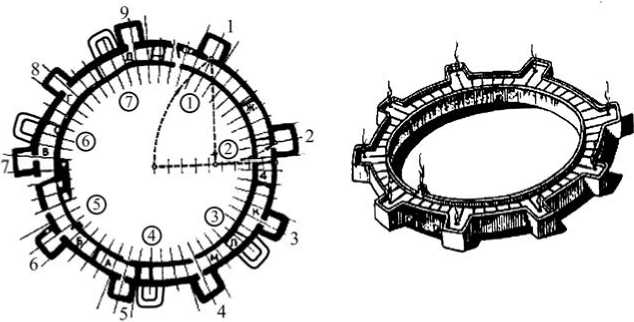
Слева – отсутствием заливки серым цветом обозначено положение башен при их полном числе; справа – аксонометрия Дашлы-3

Рис. 1. Дашлы-3. Расположение башен

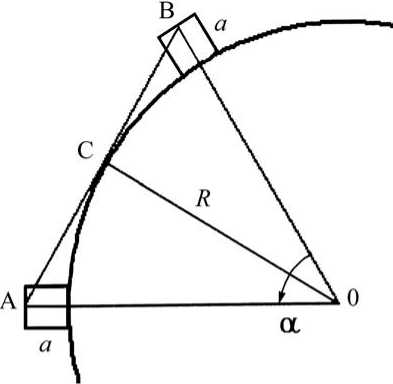
Рис. 2. Определение величины центрального угла, при котором соседние башни не простреливаются

.а ОС R 17,5

cos—=---=-----=----= 0,8974, откуда находим сам угол а = 52 ° . Тогда

,

-          А           и 360°         7

общее число башен равно                 .

52°

Математически значению n = 7 соответствует центральный угол а' = 51,4°, величина которого чуть меньше вычисленного значения а' < а = 52°. Поэтому башни окажутся немного ближе, чем показано на рис. 2. Кроме того, при расчете мы помещали наблюдателей в точки А и В, которые находятся на центральной оси. Оба этих фактора свидетельствуют о том, что если наблюдателя поставить на самый угол башни (толщину стен не принимаем во внимание), то он сможет видеть небольшую часть ближайшей к нему башни. Однако это не обеспечит возможности обороны соседней башни. Поэтому с точки зрения фортификации при n = 7 и заданных значениях радиуса внешней стены и геометрических размерах башен соседние башни простреливаться не будут. Архитекторы Дашлы-3 не учли при проектировке сооружения эту особенность. Однако когда была построена пара соседних башен, недостаток плана стал очевиден. Поэтому общее количество башен увеличили до 9, что обеспечило возможность флангового обстрела соседних башен. По нашей гипотезе, число башен на Дашлы-3 определялось именно оборонительными функциями, что подтверждается приведенными выше аргументами, объясняющими, почему сначала было построено семь ба- шен, а затем их число увеличили до девяти.

Аналогичный архитектурный анализ, примененный к памятнику Кой-Кры-лган-кала, дает принципиально отличный результат. При диаметре сооружения D = 88 м среднее расстояние между башнями составляет 30 м. Однако, в отличие от Дашлы-3, на этом сооружении башни не вынесены за периметр, а надстроены над стеной. Поэтому фланговый обстрел соседней башни невозможен ни при каком их количестве. Такая особенность конструкции значительно снижает оборонительные возможности, если сравнивать Кой-Крылган-калу с Дашлы-3. Башня № 1, находящаяся над входом в сооружение, не имеет существенного оборонного значения, поскольку вход в комплекс прикрывают две предвратные башни, вынесенные за периметр (рис. 3).

На основании этих данных мы не можем утверждать, являются ли башни Кой-Крылган-калы элементами фортификации или несут в себе некий культовый смысл. Вполне возможны оба варианта. Однако можно констатировать, что по сравнению с другими упомянутыми сооружениями оборонительная эффективность башен Кой-Крылган-калы самая низкая.

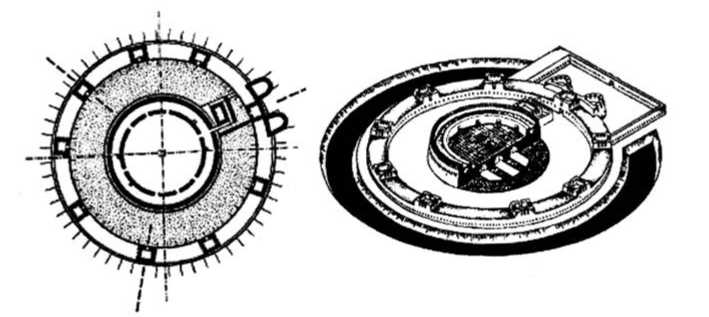
Рис. 3. Кой-Крылган-кала

Слева – план стен и расположения башен; справа – аксонометрия памятника (реконструкция М. С. Булатова)

Анализ Кой-Крылган-калы

Для анализа пространственного расположения башен мы воспользовались планами, представленными в трудах Хорезмской экспедиции (Кой-Крылган-ка-ла…, 1967. С. 23, 63). На этих планах башни пронумерованы против часовой стрелки, а отсчет начинается с предвратной башни, находящейся у входа в комплекс. Мы будем придерживаться аналогичных обозначений. На рис. 4 приведена пространственная конфигурация башен, определенная с помощью плана.

Двойное кольцо соответствует стене Кой-Крылган-калы, а черными кружками обозначены оборонительные башни (рис. 4). Направление центр – башня № 1 точно совпадает с ориентацией основной оси центрального сооружения. Внутри малого круга обозначены числа, которые соответствуют углам между соседними башнями. Например, если наблюдатель находится в геометрическом центре сооружения, то угол между башнями № 1 и 2 составляет 44º. Угол между башнями № 2 и 3 – 36º и т. д. Если предположить, что строители пытались равномерно расставить башни по окружности, получим, что каждый из центральных углов равен 360 ° /9 = 40 ° . Столь же очевидно, что вычислять среднее значение не имеет смысла, поскольку задача имеет 8 степеней свободы. Действительно, если мы расставим 9 башен и определим 8 углов, то последний, девятый, угол можно

найти из соотношения

. Проблема заключается в том, что нам

неизвестно, в каком порядке размечались углы. Быть может, последними полученными углами были те, величины которых наиболее сильно отклоняются от среднего значения, т. е. а = 47 ° , А = +7 ° или а = 34 ° (А = -6 ° ). Они могли получиться в результате накопления ошибки. Или наоборот, наиболее сильно отклоняющиеся от среднего значения углы были неправильно измерены, а девятая башня была поставлена таким образом, чтобы разделить остающийся угол пополам. Предполагая, что башни должны были быть расставлены равномерно по окружности, получим оценку среднеквадратичного отклонения положения башни о ~ 4 ° .

Впервые памятник Кой-Крылган-кала был исследован с астрономической точки зрения в работе М. Г. Воробьевой и др. (Кой-Крылган-кала…, 1967; Воробьева и др. , 1969). Авторы статьи использовали значение истинного азимута А 1 = 69 ° , на который ориентирована основная ось сооружения. Согласно нашим измерениям ( Колганова и др. , 2014), полученным с помощью спутниковых снимков Google Earth, значение данного азимута составляет А 1 = 80 ° . Ранее мы посчитали, что наиболее вероятной ошибкой авторского коллектива М. Г. Воробьевой является неправильный учет знака поправки магнитного склонения при пересчете магнитного направления на север к истинному направлению. Наше предположение оказалось верным, однако М. Г. Воробьева только воспользовалась неправильным значением азимута, а ошибку допустил архитектор М. С. Ла-пиров-Скобло, который составлял план сооружения. «В хорошо сохранившемся нижнем этаже имелось восемь помещений, из которых два (I и V) вытянуты по главной оси памятника (азимут ее 74 ° 30‘ магнитного, 69 ° истинного меридиана), остальные шесть (II и III, IV и VIII, VI и VII) симметрично распределены относительно главной оси» (Кой-Крылган-кала…, 1967. С. 23).

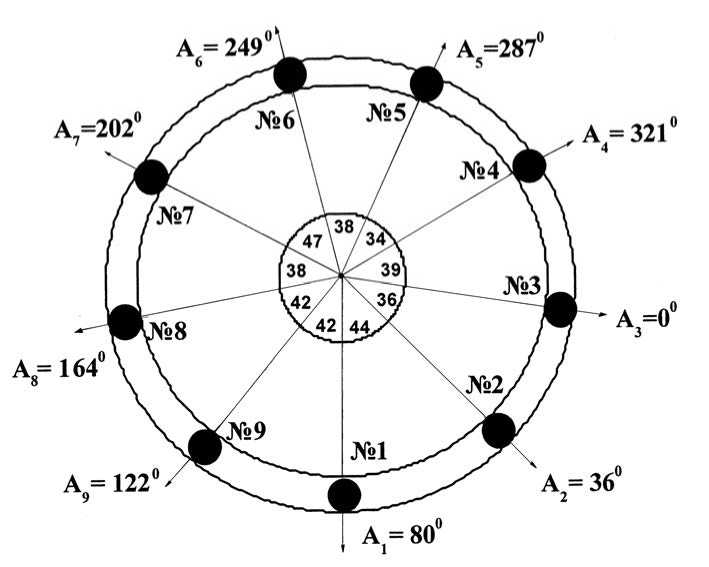
Рис. 4. Кой-Крылган-кала. План укрепления стены

М. С. Лапиров-Скобло вычел из магнитного азимута поправку а = 5 ° 30‘. Однако поскольку Хорезм имеет восточную поправку магнитного склонения, то ее следует прибавить к значению магнитного азимута. В итоге получим результат, который мы нашли по снимкам Google Earth: А 1 = 80 ° .

Азимут А ₁, проведенный через геометрический центр сооружения и центр башни № 1, совпадает с главной осью центрального помещения, поэтому его значение равно А 1 = 80 ° . Зная этот азимут и измеренные углы между башнями, можно найти восемь остальных азимутов. На рис. 2 вычисленные азимуты обо-начены с внешней стороны кольца, изображающего стены и башни.

Отметим, что археологический план, по которому мы определяли азимуты, составлен с некоторой погрешностью. Она складывается из погрешности ориентации плана и погрешности измерения углов. Погрешность ориентации плана в большей степени определяется точностью определения магнитного севера. Для теодолита с буссолью эта погрешность составляет ε ₁ = 30 ′ . Погрешность измерения углов ε ₂ зависит от цены деления шкалы измерительного прибора, характеристики которого нам неизвестны. Наконец, азимуты, которые мы находим с помощью археологического плана, также подвержены ошибке ε ₃. Ранее мы оценили ( Колганова и др. , 2014) погрешность определения азимута разными исследователями по одним и тем же снимкам Google Earth величиной А А = 1,7 ° .

Складывая все виды погрешностей ε ₁, ε ₂, ε ₃, осторожно оценим величину полной ошибки в диапазоне е total ~ 2 ° на уровне 1 о .

Измеренный азимут А 1 = 80 ° соответствует направлению гелиакального восхода Плеяд А = 79 ° , которые в древнем Хорезме были маркером майского паводка Амударьи (Там же). Кроме того, по данным М. С. Андреева, Плеяды в Средней Азии использовались в качестве маркера начала лета, а также начала и окончания зимы ( Андреев , 1958. С. 172, 173).

Измеренный азимут А 3 = 0 ° точно соответствует направлению на истинный север А ₃ = А_N , которое является астрономически значимым. Измеренный азимут А 9 = 122 ° в точности соответствует азимуту восхода Солнца в летнее солнцестояние на широте Хорезма. Совпадение этих трех азимутов с истинными астрономическими направлениями получилось достаточно точным. Измеренный азимут А 5 = 287 ° соответствует азимуту гелиакального захода Плеяд А 5 = 283 ° , а направление А 6 = 249 ° соответствует азимуту захода Солнца в зимнее солнцестояние А 6 = 238 ° . Отметим, что измеренные азимуты А 5 и А 6 отличаются от истинных азимутов. Вероятно, это вызвано погрешностью установления местоположения башен. Таким образом, можно объяснить 5 из 9 присутствующих на памятнике направлений.

Оставшиеся азимуты не могут быть отождествлены с явлениями в движении Солнца и Луны. Практически всегда можно предложить какие-то звезды, которые восходят или заходят на нужном направлении в заданную историческую эпоху. Поэтому нет никакого смысла заниматься подобным перебором.

Очевидно, что, определив пять азимутов, характеризующих направление на север, гелиакальный восход и заход Плеяд, а также азимуты восхода и захода Солнца зимнего солнцестояния, можно получить несколько модулей угловых расстояний. Угол между башнями № 3-1 составляет 80 ° , угол между башнями № 3-9 равен 122 ° , а угол между башнями № 1-9 - 42 ° . Делая небольшое округление, получаем модуль углового расстояния между башнями 42 ° ~ 40 ° и их количество n = 360 ° /40 = 9 ° .

Резюмируем результаты в табл. 1, где для каждой башни выпишем три азимута: азимут, измеренный с помощью археологического плана, А_изм ; азимут, которому соответствует определенное астрономическое событие, А_астр , и азимут, получаемый при равномерном разбиении периметра девятью башнями с отсчетом от северной башни, А_равн .

Две колонки невязок А_изм-А_равн , А_астр-А_равн соответствуют разностям азимутов из предыдущих колонок. Невязка А_астр-А_равн показывает, что равномерное разбиение окружности девятью башнями достаточно хорошо соответствует астрономически значимым азимутам. В трех случаях³ отклонение азимута не превышает заявленную погрешность | А_астр-А_равн | ≤ ε_total на уровне 1 σ , а для башни № 8 находится в пределах 2 σ . То есть сама концепция – аппроксимировать пять астрономических азимутов равномерным разбиением окружности модулем углового расстояния а = 40 ° - вполне работает. С другой стороны, невязки колонки

А_изм-А_равн показывают, что башни № 7 и 8 были поставлены не очень точно, что может объясняться ошибками при разметке и строительстве.

Таблица 1

Башня, №	А изм	А астр	А равн	изм равн	астр равн	Событие
1	0	0	0	0	0	Север
2	36	–	40	-4	–	–
3	80	79	80	0	-1	ГВ Плеяд
4	122	122	120	2	2	ВС ЗСС
5	164	–	160	4	–	–
6	202	–	200	2	–	–
7	249	238	240	9	-2	ЗС ЗСС
8	287	283	280	7	3	ГЗ Плеяд
9	321	–	320	1	–	–
Примечания : ГВ, ГЗ – гелиакальный восход или заход Плеяд; ВС/ЗС ЗСС – восход или заход Солнца в зимнее солнцестояние

Заключение

При сооружении Кой-Крылган-калы использовалась хорошо известная среднеазиатская архитектурная традиция строительства крепостей и оборонительных сооружений с рядом стандартных элементов – башнями, стрелковыми галереями, сложными системами предвратных лабиринтов. Используя традиционные архитектурные приемы, строители памятника решали одновременно и другую задачу, а именно сооружение крупного культового объекта, одной из важнейших функций которого были астрономические наблюдения.

Исследование пространственной ориентации башен памятника Кой-Крыл-ган-кала показало, что в его архитектуре можно выделить пять астрономически значимых азимутов. Это азимут астрономического севера, азимуты восхода и захода Солнца в день зимнего солнцестояния и азимуты гелиакального восхода и захода Плеяд. Данные направления можно было «зашифровать» девятью равномерно расставленными по окружности башнями. Наша гипотеза заключается в том, что такая схема возникла не случайно, а была реализована специально архитекторами памятника Кой-Крылган-кала.