Элементы оценки ресурса стальных балок, предварительно напряженных вытяжкой стенки

Теоретические основы оценки ресурса конструкций представлены в работах В.В. Болотина [1], А.Г. Райзера [2], А.Р. Ржаницина [3], А.В. Перельмутера [4, 5], А.А. Ройтмана [6].

Практические приемы определения ресурса конструкций зданий и сооружений разработаны ведомственными организациями [7, 8], в том числе Министерством строительства и жилищно-коммунального хозяйства Российской Федерации [9], РУСПРОМ (Эксперт) [10], Федеральной службой по экологическому, технологическому и атомному надзору [11], в ЦНИИпро-ектстальконструкция им. Мельникова [12, 13], ЦНИИпромзданий [14], ЦНИИСК им. В.А. Кучеренко [15].

Большой вклад в разработку инженерных методов расчета остаточного ресурса строительных конструкций вносят научные коллективы Волгорадского архитектурно-строительного университета [16], Пермского национального исследовательского политехнического института [17], Белгородского государственного технического университа им. В.Г. Шухова [18], Санкт-Петербургского политехнического института им. Петра Великого [19], Тамбовского государственного технического университета [20], Южно-Уральского государственного университета [21, 22].

Работу в этом направлении выполняют вузы Владивостока [23], Казани [24], Полоцка [25], Санкт-Петербурга [26], Улан-Удэ [27 - 30], следует отметить иностранные публикации [31].

Отметим также работы по оценке ресурса строительных конструкций [32, 33], в которых предложен метод пробной нагрузки замерами твердости металла эксплуатируемой конструкции.

Рекомендации по градостроительному планированию оптимальных сроков выхода зданий из эксплуатации и их сносу, новому строительству, капитальному ремонту, реконструкции на основе алгоритма оценки снижения остаточного ресурса надежности по параметрам цикловой усталости представлены в диссертации И.Ю. Майстренко [34].

Методом конечных элементов описаны модели оценки степени безопасности и риска разрушения металлических ферм с предложением диагностического признака предразрушаю-щего состояния конструкций описан в работе [35]. Расчет остаточного ресурса строительных конструкций с учетом коррозионного и физического износов, ресурса по статической прочности и усталости предложен в исследовании [24].

Особенность работы конструкций при случайных отклонениях и от проектных решений, а также влияние работоспособности отдельных конструктивных элементов на несущую способность здания в целом описаны в работах [36, 37].

Помимо этого, проведенный обзор литературы по исследуемой тематике выделяет ряд публикаций, которые, на наш взгляд, достаточно убедительно дают оценку ресурса строительных металлических конструкций [38, 39] и инженерного метода расчета остаточного ресурса строительных конструкций [17].

Установлено, что существующие и наиболее разработанные методики определения остаточного ресурса металлических конструкций базируются на теории вероятности и математической статистике с учетом детального анализа степени физического и морального износа конструкций.

Цель работы: предложить методику определения ресурса стальных балок, предварительно напряженных вытяжкой стенки.

На базе теории расчета стальных тонкостенных балок, предварительно напряженных вытяжкой стенки, сделан вывод о возможности определения остаточного ресурса конструкций на основе результатов их оптимального проектирования, обеспечивающего максимальную несущую способность, выносливость, хладостойкость, коррозионную стойкость, динамическую прочность балок, при эксплуатации их в экстремальных условиях Дальнего Востока.

Материалы и методы исследования

Для оценки несущей способности предварительно напряженной балки сравним ее с несущей способностью балки, не имеющей предварительного напряжения.

Предельный момент внешней нагрузки определим на основе теории сооружений, суть которой состоит в том, что момент внешних нагрузок M_{x . ob} должен быть уравновешен моментом внутренних усилий [ M ob ] .

Задача решается на основе анализа эпюры максимальных нормальных напряжений в балке с симметричным поперечным сечением (рис.).

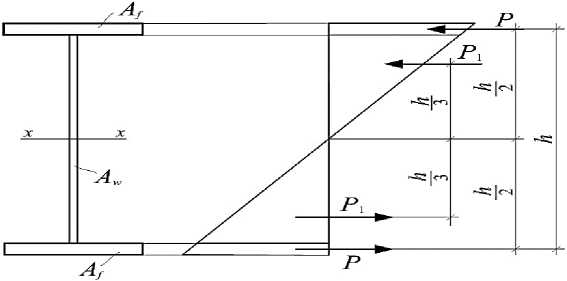
Рисунок - Нормальные напряжения в разрезной монометаллической однопролетной балке

M xob ^ [ M ob ] = Ph + fly,                         (1)

где P , P 1 — внутренние усилия, действующие по центру тяжести, соответственно поясных листов и стенки балки; h ,2 h /3 — плечи внутренних усилий.

Площадь поперечного сечения симметричного двутавра

A = 2 A f + A w .                                    (2)

Введем коэффициенты, характеризующие распределение материала по поперечному сечению двутавра

• y _f = A _f / A — в поясных листах;

Y = A , / A — в стенке балки. ww

С учетом коэффициентов:

• —    площадь поясного листа — A f = у f A;

• —    площадь стенки — A w = y _wA .

Подстановка выражений, характеризующих соответствующие площади элементов балки, в зависимость (2) позволяет выразить коэффициент у f через коэффициент y _w

1 — у г f = -2 - w .                                      (3)

Усилие P , действующее в верхнем и нижнем поясах балки,

^P = R y A f = R y Y f^A = R y A —Yw- .                        (4)

Усилие P ₁ , сосредоточенное в центре тяжести эпюры нормальных напряжений по

стенке балки, p - 1v htw p -1. AWRy _YwARy_

Pl      x ^Rv *                      .

1 22 y 2  2     4

В таком случае момент внутренних усилий в поперечном сечении балки R Ah

[ M ob ] = Ph + P * у — ^2 .

Сопоставляя выражение (6) с известной записью момента внешних нагрузок M — RW x ,

устанавливаем, что момент сопротивления поперечного сечения симметричной балки можно

определить зависимостью

Ah 3 - 2 / W — x w . . x 2      3

Высота сечения балки может быть определена выражением

^{h —} 4^Aw n w ,

где n_w - гибкость стенки балки.

С учетом коэффициента распре делени я матер иала по стенке балки ^{h —} 4 Y w An w = / w' 4An W .                               (8)

Подставим высоту h по зависимости (8) в выражение момента сопротивления (7)

Wx — AAAA ■ УА 2

Оптимальное распределение материала по сечению стенки балки / w определяем посред-

ством дифференцирования зависимости (9)

dW    А.Ап Г 3 6 ,/2

1           Г о 1/1 л Y w dYw      6   [2 *Yw   2

Выражение (10) позволяет установить, что

Y w, — 0,5.

С учетом / Wp оптимальное распределение материала по поясам симметричной балки

1 —у

Y f —   / — 0,25.

Момент внутренних усилий в таком случае

[ M ob ] = A x .An y- /'Ax³- / - R y — 0,2357xAR_yJAd .

Используя приведенный прием, В.А. Кравчук определил, что предельный момент внутренних усилий предварительно напряженной балки определяется выражением

[ M ,, ] =0,427 x AR yj A p ,                               (14)

где n_pr - гибкость стенки предварительно напряженной балки; R y — расчетное сопротивление материала стенки балки).

Отношение предельных моментов

M

^{£ —} M

pr

ob

0,427 - A ^3/2 R y n , 7 ₌₁₈₁ n^

0,2354 - A^3/2R y n - b ²     , n ob²’

С учетом коэффициента £ первое предельное состояние предварительно напряженной балки следует записать

& ^— R y&c .

Следовательно, ресурс несущей способности предварительно напряженной балки будет оцениваться коэффициентом

X = —~— — 1,0 . R y Y

Если % = 1,0 , то ресурс предварительно напряженной балки по первому предельному состоянию повышается на коэффициент £ = 1,81 - n ^/² / n 1 /,² и конструкция находится в предельном состоянии; при % >  1,0 , конструкция находится в запредельном состоянии, а при % <  1.0 предварительно напряженная балка обладает повышенным ресурсом несущей способности.

Жесткостью изгибаемого элемента можно назвать его способность противостоять прогибам, вызванным внешней нагрузкой.

Проблемой жесткости предварительно напряженных конструкций занимались многие крупные ученые в области металлостроительства.

Е.И. Беленя в работе «Предварительно напряженные металлические конструкции» отмечает: «… предварительное напряжение позволяет повысить эффективность конструкции, т. е. увеличить их несущую способность и в ряде случаев и жесткость», и далее — «... созданием предварительного напряжения обратного знака можно повысить жесткость конструкции».

Независимо от конструктивного решения балок и выбора материала для формообразования сечения модуль упругости сталей любого класса - E = 21000 kH / см 2 . Следовательно, жесткость сечения любой балки зависит от ее прогиба.

Прогиб балки, не имеющей предварительного напряжения, определяется известной формулой:

5    qnl4    5    1  ql2

Уп h =--х —---= — х---— х-- ob 384  EIx   48  уf  8

где qⁿ = q / y f — нормативная равномерно распределенная нагрузка; q — расчетная равномерно распределенная нагрузка; у f — коэффициент надежности нагрузки, у f = 0,9 (табл. 7.1, СП 20.13330.2017).

Выше (13) установлено, что моменту внутренних усилий

Mob = \ = 0,2357 х ARyjAnW =0,2357 х Ry A3/2 n W/2 , где nw — гибкость стенки балки.

Следовательно, прогиб обычной балки

У о Ъ= — х — х 0,2357 х R_VA ^3/2 n 1/2 х---= 0,02728 х- R_VA ^3/2 1 ² n 1'2 / EI_X .

ob                       y w            ,           y         w x

Прогиб балки, предварительно напряженной вытяжкой стенки \ у следует определять с учетом выгиба f ₀ , полученного балкой на стадии ее предварительного напряжения,

X У = У д ^{— f} ) ,

где y_g - прогиб предварительно напряженной балки от внешней, равномерно распределенной нагрузки.

5      1              l ²

У„ = — х--х М„ х--- .

g 48 г f g EI x

На этом этапе уместно выявить, какую долю в предельном моменте внешней нагрузки

M _g составляет M ₀

ql ² 8

На основании теории сооружений момент внешних нагрузок равен моменту внутренних усилий. В работе В.А. Кравчука («Стальные стержни, предварительно напряженные без затяжек», 2015) установлено, что момент внешних нагрузок предварительно напряженной балки

M g = 0,427 x R_yA ^3/2 ^n W / 2 _r .

Следовательно, отношение

M 0

Mpr

0,2357 x R_vA^3/2

-= 0,552. 0,427 x RA ^3/2

ql ²

Откуда M = 0,552M , или —— = 0,552 x M . Поскольку предварительно напряженная балка o            pr         8

нагружается предельно допустимой нагрузкой, то

Mnr= ql— x — = 1.8xql— = 1,8x0,2357xRVA3/2 JnZ = 0,427xRv A3/2 JnZ.

pr 8   0,552        8                  y w           yw

В таком случае прогиб предварительно напряженной балки, находящейся под воздействием внешней нагрузки,

5 l ²

y g = 48 EI_x

x 0,427 x R_VA ^3/2_A/ n Z = 0,04448 x R_VA ^3/2. ZZ • l ²1 EI .

y   w     yw x

Выгиб балки на стадии изготовления конструкции

fo =

M o l ²

8,3 EI xt

где M_o — момент усилий предварительного напряжения, M _o

R_yAhK ²

------:------; K — коэффици-( K + 1)²( K + 2)

ент асимметрии поперечного сечения предварительно напряженной балки K = 1,175; Ixt — мо- мент инерции сечения тавра, исходного элемента балки.

I = I _x (2 ^K + ¹) = I x ^{xt x} 2( K + 1) 1,2985,

С учетом коэффициента асимметрии K = 1,175 момент усилий предварительного напряжения

M ₀ = R_yAh x 0,092.

В таком случае с учетом Ixt по зависимости (27) выгиб fo =

0,092 x R_yAh x l ²

8,3EI x

x 1,2985 = 0,119462 x

RyAhl2 EIx

Известно, что высоту поперечного сечения двутавра можно определить по формуле:

h = 7 0,496 x An_w = 0,70423 x A ^1/2 T n Z .

В итоге выгиб предварительно напряженной балки на стадии ее изготовления

f_o = 0,119462

R_yAl ² x 0,70423 x A ¹/² T n Z

8,3EI x

= 0,0101 x

RyA3/2l2 nw EIx

Результирующий прогиб предварительно напряженной балки, фиксируемый в середине конструкции, с учетом зависимостей (25) и (28)

E y ^- y g

- f о -

R A 3/2 l 2                                           R A 3/2 l 2

------wp o (0,04448 - 0,0101) - 0,0343 8 • —------ w"'

EIx                                         EIx

Соотношение суммарного прогиба E y предварительно напряженной балки, нагружен- ной внешней нагрузкой Mg , и прогиба yg при той же нагрузке может быть характеристикой ее жесткости

E у

V 0 ----- yg

0,03438

0,04449 •

- 0,7729.

Это означает, что прогиб предварительно напряженной балки снижен в 0,7729 раза, или жесткость балки повышена в 1/0,7729 - 1,2937 раза.

Выводы, изложенные выше, относятся к конструкциям, шарнирно закрепленным в опорных узлах. Если указанные узлы балок будут жестко закреплены в опорных узлах конструкции, то появится еще выгиб yop, вызванный опорным моментом, вектор которого направлен в сто- рону, противоположную вектору внешней нагрузки. В этом случае результирующий прогиб

предварительно напряженной балки

R_yl 2 A 3/2 n 1/2

E У ^- y q ^{- (} f₀ + У ор )  ----—-----

EIx

ql ²

В формуле ⁽³¹⁾ y o _p ^-

24 EI _x

R l 2 A 3/2 n 1/2

((0,04448 • -(0,0101 + 0,0297) - 0,01478 х -У----------- EIx ql2 1    1    l2            A3/2Rn1/2

( xl - x )  --- х-х---х— - 0,2357 х----------

8   3 EI_x   4               EI_x

l ²

х---

0,0297 х

R _y l ² A ^3/2 EI x

n 1/2

.

Из выражения (31) следует, что при жестких опорных узлах суммарный прогиб предварительно напряженной балки дополнительно снижается еще на 42,9 %. Для того чтобы предварительно напряженная балка заняла «нулевое» положение, а затем получила классический прогиб, к ней необходимо приложить внешнюю нагрузку, многократно превышающую нагрузку для обычных балок. Отсюда следует логический вывод: ресурс жесткости балок, предварительно напряженных вытяжкой стенки, выше ресурса жесткости обычных балок.

Из зависимости (30) следует, что ресурс жесткости предварительно напряженных балок, шарнирно закрепленных в опорных узлах из условия обеспечения второго предельного состоя- ния,

&_h - ^ y - ^0,03438 - 0,773.

^sh     y_g    0,04448

Изложенное дает основание для утверждения, что ресурс предварительно напряженной балки повышается, эксплуатационные нормальные напряжения можно повысить на коэффициент х, а относительные деформации снизить на коэффициент & . Представляется, что на стадии сопоставительного анализа предложенная методика вполне убедительно показывает уровень повышения ресурса балок, предварительно напряженных вытяжкой тонкой стенки.

При решении задач, касающихся выяснения ресурса предварительно напряженных балок, весьма показательным может быть соотношение их высот.

Для решения задачи воспользуемся выражением суммарного прогиба предварительно напряженной балки (29).

Заметим, что момент инерции балки можно определить зависимостью

I, = 2 x

x

Ah ² K

3  ( K + 1)

= 0,16558 x Ah ².

Учитывая (32), суммарный прогиб предварительно напряженной балки запишем:

R l 2 A 1/2 n 1/2

Z y = 0,2 x        ----

.

Eh ²

Требуемая площадь поперечного сечения балки A определяется зависимостью

A = 3

2 M pr       3	(1,8 ql 2)2 8
0,4272 x R y n w V	0,4272 R y 2 n w

q 2/3 l 4/3

= ^{0,6524 x}_R2/3 1/3 y n

2/3 4/3                1/3 2/3

A"¹ = V0,⁶⁵²⁴       = 08077 x q^ .

Ry n

.

Подставим (35) в выражение прогиба по зависимости (33)

2/3 8/3 1/3 1/3 Rlqn

Z y = 0,16154 x -------------

Eh ²

.

Введем понятие «относительный прогиб», т. е. почленно разделим выражение (36) на пролет балки l

2/3 5/3 1/3 1/3 Rlqn

Zy = 0,16154 x---y---------- l                    Eh2

.

Полученная зависимость позволяет определять высоту поперечного сечения предварительно напряженной балки h при вариации пролета l и равномерно распределенной

нагрузки q

h =

0,16154 • R231 5/3 q 1/3 n 1/3

E [ Z y 1      . E •

L1 J

Допуская, что расчетное сопротивление материала стенки предварительно напряженной балки Ry - 23kH / см2 , модуль упругости стали E = 21000kH/ см2 , гибкость стенки балки nw = 150, а относительная гибкость балки пролетом I = 12000 мм - Z У /1 = 0,004 (см. табл. Л.1. СП 20.13330.2017), высота балки будет определена зависимостью h = 0,28735x]15/3q1/3 .                                (39)

Численные значения высот предварительно напряженных балок h при вариации пролета l и внешней равномерно распределенной нагрузки q приведены в таблице.

Таблица

Высота h предварительно напряженной балки, см

q, kH/см	l=6000 мм	l=9000 мм	l=12000 мм
0,02	31.0	43,4	55,1
0,04	34,7	48,7	61,8
0,06	37,1	52,1	66,2
0,08	39,0	54,7	63,4
0,18	44,6	62,6	79,4

Взаимосвязь высоты предварительно напряженной балки h и высоты балки, не имеющей предварительного напряжения h_ob , выясним из рассмотрения соотношения требуемых площадей поперечного сечения сопоставляемых конструкций.

Известно, что требуемая площадь сечения обычной балки может быть определена выражением

A tr ob

M ²

31 0,2357 2 R²_y n.

^, w . ob

а предварительно напряженной - tr Apr

M ²

3| 0,427 2 R 2 n w^r

.

При условии, что обе балки нагружены одинаковым моментом M , при гибкости стенки обычной балки n_{w ob} = 80, а гибкости стенки предварительно напряженной балки n_wpr = 150 , отношение площадей поперечных сечений сопоставляемых конструкций

A

A

pr

об

2/3    1/3

0,427^2/3 • n

На основании теории оптимального проектирования сопоставляемых балок установлено, что

^Y w . pr

требуемая площадь сечения стенки

предварительно напряженной балки

Поскольку A pr = 0,546 x A ob , то площадь

стенки предварительно напряженной балки A w pr = 0,496 x 0,546 x A ob = 0,27 • A ob .

Оптимальная площадь стенки обычной балки - wob^ ^ ^x ^ ^ob ’

Соотношение площадей стенок предварительно напряженной и обычной балок

A     = 0.27A b = 0,541.

Запишем соответствующие площади сечений стенок балок как произведение их высот, умноженных на толщины стенок.

ht =0,541-Л J _h. w . pr      ,           ob w . ob .

При равенстве толщин сопоставляемых балок hob = hpr /0,541 = 1,848h .

Таким образом, можно утверждать, что ресурс высоты предварительно напряженной балки в 1,848 раза выше ресурса высоты балки, не имеющей предварительного напряжения.

Вместе с тем нельзя не отметить, что уменьшение толщин стенок предварительно напряженной и обычной балок сопровождается уменьшением отношения высот сопоставляемых балок. Например, если толщина стенки предварительно напряженной балки в два раза меньше толщины обычной балки, то hob = 0,5hpr /0,54 = 0,926 x hpr.

Следовательно, снижение толщины стенки предварительно напряженной балки ведет к снижению соотношения высот балок и снижению ресурса предварительно напряженной балки.

Заключение

Стальные однопролетные балки, предварительно напряженные вытяжкой стенки, можно рекомендовать для применения в качестве балок покрытий и перекрытий стальных каркасов жилых и общественных зданий и сооружений, а также прогонов зданий промышленного назначения.