Эллиптические уравнения с инволютивным отклонением аргумента

В последние десятилетия исследование дифференциальных уравнений с отклоняющимся аргументом, особенно тех, которые имеют инволютивное отклонение, стало одним из наиболее динамично развивающихся направлений.

Отображение ^ ( t ) , для которого ^ 2 ( t ) = ^(^(t)) = t, называется инволюцией или инволютивным отображением (см. [1]).

Теория краевых задач для дифференциальных уравнений, имеющих инволюцию, была предметом изучения многих исследователей (см., например, [2–22] и библиографию в них). В работах [2–5] изучены вопросы корректности задач и качественные свойства решений уравнений с инволюцией. Исследованию разрешимости и свойств решений как

^# Исследование выполнено при финансовой поддержке Внутреннего гранта КБГУ, договор № 8. (0 2025 Бжеумихова О. И.

обыкновенных дифференциальных уравнений, так и уравнений в частных производных с инволютивным отклонением аргумента, были посвящены статьи [6–19]. Отметим, что в работах [20–22] изучались спектральные задачи для дифференциальных уравнений с инволюцией. Заметим, что большинство указанных статей посвящены одномерным задачам для уравнений с постоянными коэффициентами и с линейной инволюцией.

Операторы с инволюцией возникают в некоторых геометрических задачах [23, с. 98], в теории фильтрации [24, с. 61], теории прогнозирования и при изучении субгармонических колебаний [25, с. 271].

Изучаемые в настоящей работе дифференциальные уравнения с инволюцией, а также методы исследования краевых задач для них имеют существенные отличия от известных ранее. Ранее они рассматривались лишь в случае уравнений с постоянными коэффициентами и с линейной инволюцией, в которых основным методом исследования был метод Фурье. В данной статье доказаны теоремы существования решений краевых задач для эллиптических уравнений с переменными коэффициентами и с общей инволюцией по выделенной переменной в цилиндрической области. Также в работе для одного частного случая исследовано влияние параметров эллиптических уравнений с инволюцией на единственность и неединственность решений краевых задач. Получены теоремы, определяющие условия единственности и неединственности решений.

• 2.    Постановка задач

Пусть Q — ограниченная область из пространства Rn переменных xi, Х2,..., xn с гладкой границей Г. В цилиндрической области Q = Q х (0, T), 0 < T < +го, рассмотрим дифференциальное уравнение utt(x, t) + Au(x, t) + a(x, t)u(x, t) + b(x, t)u(x, ^(t)) = f (x, t),              (1)

где a(x,t) , b(x,t) и f (x,t) — заданные функции, определенные при x G Q , t G [0 , T ] , ^(t) — заданная на отрезке [0 , T ] инволюция, A — оператор Лапласа, действующий по переменным x 1 , x 2 , . . . , x _n .

Задача 1. Найти решение u(x,t) уравнения (1) в области Q, удовлетворяющее условиям

u(x,t) |s = 0,(2)

u(x, 0) = 0, u(x,T) = 0, x G Q,(3)

где S = Г х (0 ,T ) .

Задача 2. Найти решение u(x,t) уравнения (1) в области Q, удовлетворяющее (2), а также условиям ut(x, 0) = 0, ut(x,T) = 0, x G Q.(4)

Задача 3. Найти решение u(x,t) уравнения (1) в области Q, удовлетворяющее (2), а также условиям

u(x, 0) = au(x,T), ut(x,T) = 0, x G Q,(5)

где α — действительное число.

Заметим, что в случае а = 1 тождества (5) представляют собой нелокальное условие Ионкина [26].

Задачи 1 и 2 хорошо изучены в случае b(x,t) = 0 (см., например, [27]). Если же b(x, t) = 0 и при наличии переменных коэффициентов разрешимость краевых задач 1 и 2 для уравнения (1) представляется неизученной.

Нелокальные задачи для эллиптических уравнений без инволюции были исследованы А. Л. Скубачевским [28, 29], А. К. Гущиным и В. П. Михайловым [30], а их разрешимость в работах в [31, 32]. Отметим, что для таких задач с инволюцией подобные вопросы ранее не затрагивались.

• 3.    Исследование разрешимости задач

Пусть w(x) принадлежит пространству W 2 ¹ (Q) . Имеет место неравенство

У w ² ( x, t) dx <  c o

Ω

n z i =1 _Ω

w X i (x, t) dx

с постоянной c o , определяющейся лишь областью Q [33].

Доказательство разрешимости исследуемых задач будем проводить методом продолжения по параметру [34, с. 146] и априорных оценок.

Для задачи 1 справедлива следующая теорема.

Теорема 1. Пусть для функций a(x,t) , b(x,t) и ^(t) выполняются условия:

a(x,t) G C(Q), b(x,t) G C(Q), ^(t) G C 1([0,T]),(7)

a(x,t) < 0 при (x,t) G Q, —^1 < ^(t) < —^o < 0 при t G [0, T],(8)

+7777 - min a(x,t) — ^^1 max |b(x,t)| > 0.(9)

• c0 T2    QQ

Тогда для любой функции f (x,t) G L 2 ( Q ) задача 1 имеет единственное решение u(x,t) G W 2 (Q) .

• <1 Пусть p = const G [0 , 1] . Рассмотрим вспомогательное семейство краевых задач: найти функцию u(x, t) , являющуюся в области Q решением уравнения

u _tt (x, t) + A u ( x, t) + a(x, t)u(x, t) + pb(x, t)u(x, ^(t)) = f (x, t),            (10)

и удовлетворяющую условиям (2) , (3) .

Согласно теореме о методе продолжения по параметру, краевая задача (10), (2), (3) будет разрешима в пространстве W 2 (Q) при принадлежности функции f (x,t) пространству L 2 (Q) для всех чисел p из отрезка [0 , 1] , если:

• 1)    задача (10), (2), (3) разрешима в пространстве W 2 (Q) при p = 0 ;

• 2)    для всевозможных решений u(x,t) краевой задачи (10), (2), (3) имеет место равномерная по ρ априорная оценка

  
  

llullw22(Q) ^ Mo Ilf^L2(Q), с постоянной Mo, определяющейся функциями a(x,t), b(x,t) и ^(t), а также областью Q и числом T .

Хорошо известно, что при p = 0 задача (10), (2), (3) разрешима в пространстве W 2 (Q) при выполнении условий (7), а также условия 1 /c o + 2 /T ² — a(x,t) >  0 (условие выполняется вследствие (9)) [27].

Покажем теперь, что для всевозможных решений u(x,t) краевой задачи (10), (2), (3) имеет место равномерная по ρ оценка (11).

Рассмотрим равенство

- У [utt (x, t) + Au(x, t) + a(x, t)u(x, t) + pb(x, t)u(x, ^(t))] u(x, t) dxdt

Q

= — J f (x, t)u(x, t) dxdt.

Q

Применяя формулу интегрирования по частям с учетом условий (2), (3), получим

— p J b(x,t)u(x,^(t))u(x,t) dxdt = — У f (x,t)u(x,t) dxdt.

QQ

Принимая во внимание (6), а также неравенство

У ^u2 ( ^{x,t )}

Q

dxdt ^     / u2(x,t)

dxdt,

T2 Q и применяя неравенства Юнга и Гельдера, будем иметь

I: t

δ ²

u2(x,t) dxdt C — I u2(x,t) dxdt

QQ

+—I f 2(x,t) dxdt + max |b(x,t)| I / u2(x,t) dxdt] I / u2(x,^(t)) dxdt] .

2^2 J                       Q             \ J                   I \ J

Q   QQ

— min

Выполнив в последнем интеграле, содержащем инволюцию, замену z = ^(t) и учи- тывая (8), можем от (12) перейти к неравенству:

[ 1

c 0

⁺ T 2

Q

Q

u2(x, t) dxdt

Q ₂

C — У u2(x,t) dxdt + 2j2 У f2(x>t) dxdt.

QQ

Используя условия (9) и считая δ достаточно малым, из последнего неравенства сле- дует оценка

I ^u2 (x ^{,t )}

Q

dxdt C M i

У f 2(x,t) dxdt,

Q

где постоянная M i определяется функциями a(x,t) , b(x,t) и ^ ( t ) , а также областью Q и числом T .

Таким образом, из оценки (13) получаем, что для всевозможных решений u(x, t) задачи (10), (2), (3) имеет место равномерная по ρ априорная оценка (11).

Выше изложенные рассуждения означают, что краевая задача (10), (2), (3) будет разрешима в пространстве W 2 (Q) для всех чисел р из отрезка [0 , 1] , включая случай р = 1 . Следовательно, краевая задача 1 также будет иметь решение в том же пространстве.

Единственность решений краевой задачи 1 в пространстве W 2 (Q) очевидна. Теорема доказана. >

Для задачи 2 справедлива следующая теорема.

Теорема 2. Пусть выполняются условия (7) , (8) , а также условие

--min a(x,t) — /^ 1 max | b ( x,t ) | >  0 .

^c 0     Q                Q

Тогда для любой функции f (x,t) G L 2 ( Q ) задача 2 имеет единственное решение u(x,t) G W 2 (Q) .

• <1 Для чисел р G [0 , 1] рассмотрим задачу (10), (2), (4). При р = 0 и при выполнении условий теоремы 2 задача (10), (2), (4) будет разрешима в пространстве W 2 (Q) для любой функции f (x,t) G L 2 (Q) (см. [27]).

Для решений u(x,t) задачи (10), (2), (4) при всех р = 0 и при выполнении условий теоремы 2 имеет место следующая оценка:

У u 2 (x,t) dxdt + JAx.t) dxdt ^C N у f ² ( x, t) dxdt, QQ  Q

где постоянная N определяется функциями a(x,t) , b(x,t) , ^(t) и областью Q .

Из разрешимости задачи (10), (2), (4) при р = 0 в пространстве W 2 ( Q ) , а также из оценки (15) и из теоремы о методе продолжения по параметру следует разрешимость задачи 2 в том же пространстве. Единственность очевидна. >

Перейдем к изучению разрешимости нелокальной задачи 3.

Пусть α 1 и α 2 — фиксированные числа такие, что

• 1    — a = ai — a 2 ,  a i = max (1 — a , 0^ ,  a 2 = ai — (1 — a ^ .

Теорема 3. Пусть для функций a(x, t) и b(x, t) , заданной инволюции ^(t) и числа a 2 выполняются условия:

a(x,t) G C(Q)  a(x,y) C —ao < 0 при (x,t) G Q,(16)

b(x,t) G C(Q) /t\b(x,t)\ C boV^t) (V(x,t) G Q),(17)

^(t) G C 1([0,T]), —^1 C ^(t) C —^0 < 0 при t G [0,T],(18)

a2 + ^2 + 2Tb ^ . < 2Tao + T.(19)

2T     Tc

Тогда для любой функции f (x,t) такой, что f (x,t) G L 2 (Q) , f t (x,t) G L 2 (Q) , задача 3 имеет единственное решение, принадлежащее пространству W 2 (Q) .

< Следуя [32], рассмотрим нелокальную краевую задачу: найти функцию u(x,t), являющуюся в цилиндре Q решением уравнения utt(x, t) + Au(x, t) — eAutt(x, t) + a(x, t)u(x, t) + b(x, t)u(x, ^(t)) = f (x, t)     (20)

( e >  0) , удовлетворяющую условиям (2) и (5) .

Покажем, что при е € (О ,е о ) (величину числа е о уточним ниже) и при принадлежности функции f (x, t) пространству L 2 (Q) краевая задача (20), (2), (5) будет иметь решение u(x,t) такое, что u(x,t) € W 2 (Q) , Au ₍₍ (x,t) € L 2 ( Q ) . Сделаем это с помощью хороших априорных оценок.

Для получения первой априорной оценки умножим уравнение (20) на функцию -tu(x, t) и проинтегрируем по цилиндру Q. После несложных преобразований будем иметь:

nn

tut(x, t) + 52 tuXi (x, t) + aotu2(x, t) + Е 52 tuXit(x, t) dxdt

Ω

_Q               i =1                              i =1

nn

+ “f1 / ^ ^u X i ^{( x,T} ) ^{dx C} у / ^{u2 ( x,T} ) ^{dx +} “у² [ ^ ^u X i ^{( x,T} ) ^dx

_Ω i =1                   _{Ω                    Ω} i =1

+

I tbAAAA^^ dxdt

Q

+ jtux.tyf (xt) dxdt

Q

Оценим третий интеграл правой части (21) с помощью неравенства Г¨ельдера и сде- лаем замену z = ^(t):

fAxxu^^ dxdt ^C

Q

C bo V^i I У ^(t)u²(x^(t))) dxdt

Q

/ ^{tb 2} ( x,t ^{) u} 2 ( x,„ ( ^{t ))} dxdt ]  I jtAtX dxdt I

QQ

I У tu2(x,t) dxdt I = bo V^i У tu2(x,t) dxdt.

QQ

Из неравенств (21) и (22) в случае а 2 = 0 очевидным образом вытекает нужная первая априорная оценка, поэтому в дальнейшем считаем α 2 положительным.

Для произвольной функции v(x,t) имеет место следующее неравенство:

У v2(x—) dxdt C — У tv2(xtt) dxdt + ^

Ω

Q

T2 + ^2—^ У tv2(xt) dxdt,      (23)

0 _Q

где δ 0 — произвольное положительное число (для доказательства этого неравенства достаточно в равенстве

f Ax,T) dxdt=

Ω

—7 / tv2(x tt) dxdt +     / t2v(x,t)v((x,t) dxdt

T ²                    T ²

Q

Q

применить ко второму слагаемому правой части неравенство Юнга).

Используя неравенство (23) для функции u(x , T) и для каждой производной u x i (x , T ) , i = 1,...,n , а также применяя неравенство Юнга и учитывая (6) и (22), нетрудно от

неравенства (21) перейти к следующему:

01 У u2(x,T) dx + 1

-

δ ₀ ² α 2

2T

Ω

У tu2(x, t) dxdt + ^

+ a o

-?(

T ^{2 +} 5 0 T

Q

- b 0 ^√ ϕ 1

n

^ tuX. (x, t) dxdt

_Q i =1

< £0 2

< 2 <

+ £ [1 -

δ ₀ ² α 2

2T J J

Q

n

i =1

+I tu2(x,t) dxdt 2co_| J

Q

n

+^2 / E uXi (x,T) dx

_Ω i =1

T ^{2 +} 5 0 T

^ У ^ tuX.(x,t) dxdt

_Q i =1

δ2T

/ tu²(x, t) dxdt +/ f ² ( x, t) dxdt.

2 5 2 J

QQ

Условие (19), а также возможность выбора числа δ сколь угодно малым означают,

что если число ε 0 принадлежит интервалу

априорная оценка

(⁰ ; 0 2+4^) ^, то при ^£ <  ^£ o из⁽²⁴⁾

вытекает

nn

/ tu2(x, t) + tu2(x, t) +     tuX.(x, t) + £    tuXit(x, t) dxdt

_Q                           i =1                i =1

+

u2(x, T)

Ω

n

^ u2Xi (x, T)

_Ω i =1

dx <  R 1

J f 2(x,t)

Q

dxdt,

с постоянной R i , определяющейся функциями a(x, t) , b(x, t) и ^(t) , областью Q и числами α и T .

На следующем шаге умножим уравнение (20) на функцию tAu(x, t) и проинтегрируем по цилиндру Q :

nn

E tuXit(x, t) + t(Au(x,t))2 + ao E

_Q i =1                                  i =1

n

n

i =1

tuX. + £t (Aut(x, t))2 dxdt

n

⁺у E [ ^uXi^(x,T ) ^{dx +} y1 i =1 _Ω

I ., T))2dx + j t -.,    -.    . - dxdt (26)

Ω

n

< у E f< (x,T ) dx + £0 2 i =1 _Ω

Q

I l^ulxT))2 dx + у tAu(x, ■ - (x.t) dxdt.

Ω

Q

Повторив выкладки, которые привели к оценке (25), применив неравенство Юнга, а также с учетом самой оценки (25) получим из (26) следующую априорную оценку:

n

n

_Q i =1

tuXit(x, t) + t(Au(x, t))2 + st (Aut(x, t))2

+£

I (Au(x,T))2

Ω

dx < R2

dxdt +

n EJ i =1 _Ω

u2X. (x, T) dx

J f 2(x,t)

Q

dxdt,

где постоянная R 2 определяется функциями a(x,t) , b(x,t) и ^ ( t ) , областью Q и числами α и T .

Далее, умножив уравнение (20) на функцию —tAu _tt (x,t) и проинтегрировав по цилиндру Q , получим:

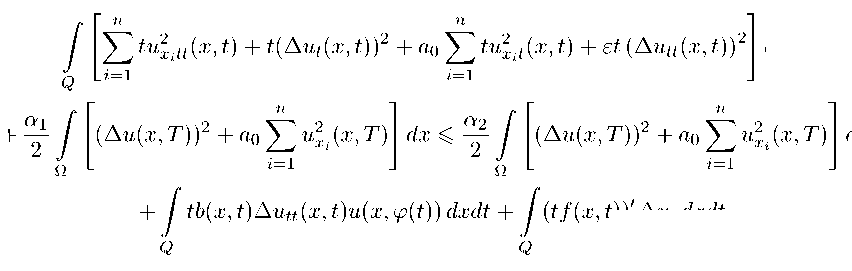
n

n

n

£ tuX^x, t) + ^{t (}^u t ⁽x, t))

+ a o 52 tu X _{i t} (x, t) + et (Au _tt (x, t)) 2 dxdt

Q

n

n

+ -^    (A u ( x,T )) ² + a o£ u X i (x,T ) dx <  ^2   (A u ( x,T )) ² + a o ^<(x,T ) dx

Ω

+ У ( tf ( x,t )) t A u t dxdt.

Q

+ J tb(x,t)Au tt (x,t)u(x,^(t')') dxdt

Q

Аналогично, повторяя предыдущие рассуждения, используя оценки (25) и (27), а также применяя неравенство Юнга, получим следующую априорную оценку:

n

52 tuXitt(x, t) + t(Aut(x, t))2 + et (Autt(x, t))2 dxdt

+ ^Auuxx,T )) ² dx <  R 3 у [ f ² ( x,t ) + f t ² ( x,t ) ] dxdt,

Ω

Q где постоянная R3 определяется функциями a(x,t), b(x,t) и ^(t), областью Q и числами α и T.

В свою очередь, из (28) следует, что выполняются равномерные по ε оценки

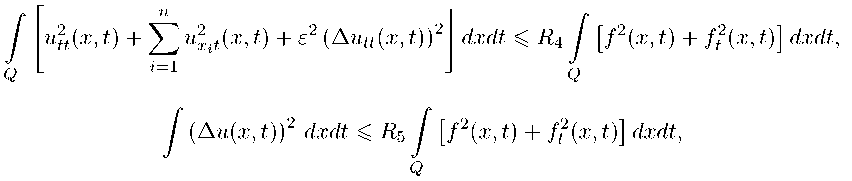
n u2t(x,t) + ^^uXit(x,t) + e2 (Autt(x,t))2 dxdt < R4   [f2(x,t) + ft2(x,t)] dxdt.

У (Au(x, t))² dxdt <  R 5 У [ f 2 (x,t) + fl(x,t)\ dxdt,

Q

Q

постоянные R 4 и R 5 , в которых определяются лишь функциями a(x,t) , b(x,t) и ^ ( t ) , областью Q и числами а и T . Данные неравенства выводятся аналогично оценкам, приведенным в работе [32].

Полученных соотношений уже достаточно для осуществления процедуры предельного перехода. Для этого выберем последовательность { e _m } “ =1 чисел из интервала (0 , Е о ) , сходящуюся к нулю. Далее, из семейства {u m (x,t)} m =1 решений краевых задач (20), (2), (5) в случае e = e m выберем подсемейство {u m k (x,t)}m_i =₁ такое, что для некоторой функции u(x,t) имеют место сходимости при k ^ от : u m k (x,t) ^ u(x,t) слабо в W 2 ( Q ) , e m k Au m k _tt (x,t) ^ 0 слабо в L 2 ( Q ) , u m k (x, 0) ^ u(x, 0) слабо в W 2 (Q) , u m k (x,T) ^ u(x,T) слабо в W 2 (Q) (в силу свойства рефлексивности гильбертова пространства это возможно). Очевидно, что предельная функция u(x,t) и будет искомым решением краевой задачи 3 при выполнении условий (16)–(19).

Единственность в пространстве W 2 (Q) решения нелокальной задачи 3 следует из оценки (25), справедливой при выполнении условия (19). Из неравенства (25) следует, что для решения u(x, t) нелокальной задачи 3 в случае f (x, t) = 0 выполняется условие

u(x, 0) = 0 , т. е. функция u(x, t) будет решением однородной краевой задачи из пространства W 2 ( Q ) для эллиптического уравнения. Следовательно, решение нелокальной задачи 3 единственно. Теорема доказана. >

• 4. Влияние параметров на корректность задачи Дирихле для эллиптического уравнения с инволюцией

Рассмотрим частный случай уравнения (1)

utt(x, t) + Au(x, t) + Xu(x, t) + ци(х, T — t) = 0,                  (29)

где λ и µ — действительные параметры.

Целью этого раздела работы является исследование влияния параметров λ и µ на единственность и неединственность решений задачи (29), (2), (3), т. е. задачи Дирихле.

Пусть {w k ( x)} k =i — ортонормированная в пространстве L 2 (ty последовательность собственных функций задачи Дирихле для оператора Лапласа с упорядоченной по убыванию последовательностью собственных чисел { Y k } k =i . Хорошо известно, что последовательности { Y k } k =i и {w k ( x ) } k = существуют и собственные числа Y k — отрицательные [35].

Обозначим через ^ km числа ^ k,m = —X — Y k + m ² n ² /T ² , где k,m G N .

Рассмотрим вначале случай X G ( —го , — Y 1 ) .

Теорема 4. Пусть X — фиксированное число из промежутка ( —го , — Y 1 ) . Тогда:

• 1)    Если | ц | <  — X — Y 1 , то однородная задача (29) , (2) , (3) имеет только тождественно нулевое решение.

• 2)    Если ц ^ — X — Y 1 и ц = ^ k,m для натуральных чисел m = 2l — 1 , l,k = 1 , 2 ,..., то однородная задача (29) , (2) , (3) имеет бесконечно много ненулевых решений, если же ц = ^ km , то задача (29) , (2) , (3) имеет только тождественно нулевое решение.

• 3)    Если ц ^ X + Y 1 и ц = —p k,m для натуральных чисел m = 2l, l,k = 1 , 2 ,... , то однородная задача (29) , (2) , (3) имеет бесконечно много ненулевых решений, если же ц = —Ц k,_m , то задача (29) , (2) , (3) имеет только тождественно нулевое решение.

• <1    Пусть для числа ц выполняется неравенство | ц | <  — X — Y 1 . Тогда при таких ц для уравнения (29) выполняются условия теоремы 3.1. Следовательно, однородная первая краевая задача для уравнения (29) имеет только тождественно нулевое решение.

Решение однородной первой краевой задачи для уравнения (29) можно представить рядом Фурье ∞

u(x, t) =     uk (t)wk (x), k=1

где функции U k (t) являются решениями следующей задачи:

^uk ^{( t ) +} ( ^Y k ^{+ X ) u} k ^{( t )} + ^цu k ^{( T —} t ) = ⁰ , t ^G f^{0 , T} ] ,

U k (0) = U k (T ) = 0 .

Дифференцируя дважды уравнение (30) с учетом равенств

Uk(T — t) = —(Yk + X)uk(T — t) — цuk(t), uk(T — t) = — ц [uk(t) + (Yk + X)uk] , получим уравнение

u k ) ^{( t )+2(} Y k + ^{A ) u} k ^{( t )} + [⁽ Y k + A ) ² - ц ² ] u k ^{( t ) — 0} , t E [0 ,T ] ,           (3³⁾

кроме того из (30) и (31) имеют место условия

u' k (0) — u k ‘ ( T ) —0 ,    k — 1 , 2 ,...

Пусть ц ^ — A — Y 1 и число ц совпадает с одним из чисел Ц k,_m для некоторых нату

ральных чисел l,k — 1 , 2 ,..., m — 2l — 1 . При таких значениях ц и A краевая задача (33),

(31), (34) имеет ненулевые решения U k,m ( t ) — A k sin Пт^ t) , где A k — const . Подставляя

U k,m (t) в (32), получим

Uk,m(T — t) — Ak sin

Tt.

С другой стороны,

πm                 πm

Uk,m(T — t) — Ak sin L — (T — t)j — ( — 1) +1 Ak sin Q — t), откуда следует, что (—1)m+1 — 1 верно для нечетного числа m.

Из приведенных рассуждений вытекает, что любая функция вида

U m,k ( x,t ) — A k sin

(ⁿm^t)w k ^{( x )}

будет решением однородной первой краевой задачи для уравнения (29) при ц — Ц k,_m с нечетным числом m.

Пусть теперь ц ^ — A — Y 1 и число ц не совпадает ни с одним из чисел Ц k,_m . Краевая задача (33), (31), (34) имеет ненулевые решения лишь в случае, когда определитель системы, порожденной условиями (31), (34), обращается в нуль, т. е. при ц — Ц k,_m . Поскольку ц — Ц k,_m , то функции U k ( t ) = 0 (k — 1 , 2 ,...) для всех t E [0 , T ] , тогда u ( x, t ) = 0 .

Проведя аналогичные рассуждения, легко проверить, что функция (35) вновь будет решением однородной первой краевой задачи для уравнения (29) в случае, если ц С A + Y 1 и ц — —Ц k,_m с четным числом m, если же ц — —Ц k,_m , то задача (29), (2), (3) имеет только тождественно нулевое решение. Теорема полностью доказана. >

Рассмотрим теперь случай A E [ — Y 1 , ^ю ) .

Теорема 5. Пусть A — фиксированное число из промежутка [ — Y 1 , го ) . Тогда:

• 1)    Если ц > A + Y 1 и ц — Ц k,_m для чисел m — 2 l — 1 , l,k — 1 , 2 ,... , то однородная задача (29) , (2) , (3) имеет бесконечно много ненулевых решений, если же ц — Ц k,_m для m — 2 l — 1 , то задача (29) , (2) , (3) имеет только тождественно нулевое решение.

• 2)    Если ц <  — A — Y 1 и ц — —Ц k,_m для m — 2 l , l, k — 1 , 2 ,... , то однородная задача (29) , (2) , (3) имеет бесконечно много ненулевых решений, если же ц — —Ц k,_m для m — 2 l , то задача (29) , (2) , (3) имеет только тождественно нулевое решение.

• 3)    Если \ц\ < A + Y 1 и ц — Ц k,_m для m — 2 l — 1 , l, k — 1 , 2 ,... или ц — —Ц k,_m для m — 2 l , l, k — 1 , 2 ,... , то однородная задача (29) , (2) , (3) имеет бесконечно много ненулевых решений, если же ц — Ц k,_m для m — 2 l — 1 или ц — —Ц k,_m для m — 2 l , то задача (29) , (2) , (3) имеет только тождественно нулевое решение.

• 4)    Если A — —Y k + n ² m ² / 2 T ² и ц — n ² m ² / 2 T ² для m — 2 l — 1 , l, k — 1 , 2 ,... или ц — — n ² m ² / 2 T ² для m — 2 l , l, k — 1 , 2 ,... , то однородная задача (29) , (2) , (3) имеет бесконечно много ненулевых решений.

• 5)    Если А = — Y k , ц = 0 , k = 1 , 2 ,... , однородная задача (29) , (2) , (3) имеет только тождественно нулевое решение.

<1 Решение задачи (29), (2), (3) при А 6 [ - 7 1 , от ) вновь определим рядом

∞

u(x,t) = ^Uk (t)wk (x).

k =i

Для функции U k ( t ) , чисел А и ц должны выполняться равенства (33), (31), (34) и (32).

Пусть ц > А + 7 1 и число А из промежутка [ — 7 1 , от ) , тогда для таких А и ц

Uk(t) = AkeCyt + Bke-Cyt + Ck cos (^Z^t) + Dk sin (yZkt), где yk = ц - А — 7k, zk = ц + А + 7k, k = 1, 2,...

Для чисел A _k , B _k , C _k , D _k с учетом условий (31), (34) выполняются равенства

A k + ^B k + C k = ⁰ ,

AkeCyT + Bke-CyT + Ck cos (yZkT) + Dk sin (yZkT) = 0,

ykAk + ykBk - zkCk = 0,

ykAkeCyT + ykBk' CyT - ZkCk cos (yzkT) — ZkDk sin (^zkT) = 0.

Определитель системы A k = — 8 ц ² sinh ( ^ y k T ) sin ( y Z k T ) обращается в нуль для всех ц = Ц k,_m . Следовательно, функции U k (t) будут ненулевыми, причем для этой функции будут выполняться условия (32) при ц = Ц k,_m с нечетным числом m. Искомыми ненулевыми решениями первой краевой задачи для уравнения (29) будут функции u m,k ( x, t) = D k sin (mT? t)w k ( x ) , m = 2l — 1 , l = 1 , 2 ,... Очевидно, что если ц не совпадает ни с одним из чисел Ц k,_m при m = 2l — 1 , то A k = 0 . Следовательно, система будет иметь только тривиальное решение и U k (t) = 0 , а значит, u ( x,t ) = 0 .

Пусть теперь ц <  — А — 7 1 и А 6 [ — 7 1 , от ) . Тогда функции U k ( t ) имеют вид

U k ( t ) = A k cos

(V—yk t) + Bk sin (V—yk t) + CkeC zk t + Dke C zk t, условия (31) и (34) порождают систему, определитель которой обращается в нуль при ц = —Цk,m. Следовательно, задача (33), (31), (34) имеет ненулевые решения Uk,m(t) = Bk sin (nm t). Тогда

U k,m (T — t) = ( — 1) ^{m +1} B k sin ( ⁿ m t ) ,                       (36)

с другой стороны, из (32)

^U k,m ^{( T —} t ) = ^—B k ^sin ( ^^t ) ,                          ⁽³⁷⁾

откуда, приравнивая правые части (36) и (37), получим, что равенство верно для четных чисел m . Таким образом, однородная первая краевая задача для уравнения (29) имеет ненулевое решение U _m,k ( x,t ) = B k sin Пт^ t)w k ( x ) при ц = —Ц k,_m для m = 2l , k,l = 1 , 2 ,... Если же ц = —Ц k,_m для m = 2l,l = 1 , 2 ,... , то система имеет только нулевое решение и U _k ( t ) = 0 , следовательно U ( x, t ) = 0 .

При | ц | < А + 7 1 имеет место равенство

U k ( t ) = A k cos (y—kk t) + B k sin ( ^— yk t) + C k cos ^fzk t) + D k sin (^ Z k t).

Вновь удовлетворяя U k ( t ) условиям (31) и (34), получим систему, определитель которой равен нулю при ^ = ± ^ k,m , причем для этой функции будут выполняться условия (32) при ^ = ^ k,m для m = 2 1 — 1 и ^ = -^ k,_m для m = 2l ( l = 1 , 2 ,...). Следовательно, краевая задача (29), (2), (3) вновь имеет ненулевые решения u _m,k (x,t) = D k sin (m^r t)w k ( x ) при ^ = ^ k,m для m = 2l — 1 и U m,k ( x,t ) = B k sin (^ t)w k ( x ) при ^ = —^ k,m для m = 2l ( l = 1 , 2 ,...). Если же ^ = ^ k,_m для m = 2l — 1 и ^ = —^ k,_m для m = 2l , то коэффициенты A k , B k , C k и D k одновременно обращаются в нуль и функции U k (t) = 0 (k = 1 , 2 ,...) при для всех t G [0 ,T ] , а значит u(x,t) = 0 .

В случае 4) непосредственно проверяется, что при А = — Y k + n ² m ² / 2 T ² и ^ = n ² m ² / 2 T ² , для m = 2l — 1 (l, k = 1 , 2 ,...) или ^ = — n ² m ² / 2 T ² для m = 2l (l,k = 1 , 2 ,... ) , задача (30), (31) будет иметь решение U k,_m (t) = A k sin (^m t) . Тогда однородная первая краевая задача для уравнения (29) имеет бесконечно много ненулевых решений.

Рассмотрим теперь случай 5). При таких значениях λ и µ легко проверить, что U k ( t ) = 0 , подставляя А = — Y k и ^ = 0 , к = 1 , 2 ,... , в уравнение (30) и удовлетворяя (31), а, следовательно, задача (29), (2), (3) имеет только тождественно нулевое решение.

Из приведенных выше рассуждений следует, что теорема полностью доказана. ⊲

• 5.    Заключение

В работе получены достаточные условия разрешимости краевых задач 1–3 для эллиптических дифференциальных уравнений с инволютивным отклонением аргумента в младших членах. Установленные результаты легко обобщаются на более общие уравнения — на уравнения с младшими производными u _t (x, t) и u x (x, t) (с соответствующими коэффициентами), на уравнения с переменными коэффициентами в старшей части.

Особое место среди изученных задач занимает задача 3. Эта задача в случае а = 1 соответствует известной задаче Н. И. Ионкина [26] (см. также [32]), исследованию которой посвящено весьма большое количество статей и диссертаций. Отметим, что в настоящей работе допускается случай а = — 1 (т. е. случай с «анти-условием Ионкина»), а также случай | а | >  1 , но при этом величина отклонения числа а от 1 определяется функциями a ( x,t ) и b ( x,t ) , размером области Q , числом T , а также собственно инволюцией ^ ( t ) .

Заметим также следующее. Имея разрешимость задачи 3, нетрудно получить разрешимость еще одной задачи Н. И. Ионкина. А именно, задачи с заменой условия (5) на условия ut(x, 0) = aut(x,T), u(x,T) = 0, x G Q.

Доказанные результаты и особенно теоремы 4 и 5 показывают, что наличие в уравнении инволютивного отклонения может существенно повлиять на условия разрешимости и вообще на корректность задачи.

Автор выражает благодарность профессору А. И. Кожанову за неоднократные обсуждения и ценные советы при выполнении данной работы.