Энергетические аспекты технологии взрывного напыления износостойких покрытий

нации. То есть процесс носит характер «увлечения» частиц продуктами детонации. В работе использовалась простая физическая модель взаимодействия продуктов детонации с частицами порошка. В основе, которой лежит неупругое соударение молекул ПД с частицами порошка. Если принять, что энергетические потери в про- цессе неупругого соударения переходят во вну- треннюю тепловую энергию частицы порошка, то можно определить количество теплоты, которое получила частица в процессе «бомбардиров- ки» ее молекулами продуктов детонации.

Законы сохранения энергии с учетом тепло- вых потерь при неупругом соударении и им- пульса можно записать в виде:

Q n ^—

mu^ М^П (M + пт)гП+1

T^-?     2

mun + (M + nm)vn — [M + (n + l)m]vn+1, (1)

n = 0, ... N , где m – масса молекул продуктов детонации; M – масса частицы порошка; u_n – массовая скорость продуктов детонации v_n – скорость частицы порошка после n- го соударения; Q_n – количество теплоты, выделившееся в процессе n-го соударения.

В соотношении (1) учитывается, что массовая скорость продуктов детонации уменьшается при расширении ПД в окружающую среду для сферического заряда ВВ по закону [4]:

u(r) — Bl r ~³ ,          (2)

где В1= 0,015, r – расстояние от центра сфериче- ского заряда ВВ.

Совместное решение уравнений системы (1)

позволяет определить

U n

Q n — "T |m"

количество теплоты Q mn i;

M + (n + l)m

+^[(M+nm)_ W^O_

• 2            M + (n + l)m]

m(M + nm)vnunM + (n + l)m

Соотношение (3) определяет лишь количество теплоты, которое было получено частицей порошка в результате однократного соударения с молекулой продуктов детонации. Однако интерес представляет полная тепловая энергия, переданная частице в результате ее взаимодействия с детонационной волной, распространяющейся в воздухе. Для этого просуммируем все Qn .

N

• 9    = ^ Q n,         (4)

n=0

где N – суммарное количество соударений молекул ПД с частицей порошка. Величина Qn определяется соотношением (3). Динамическая задача определения скорости движения частицы под действием потока молекул продуктов детонации была решена автором в работе [4]. График зависимости скорости частицы от расстояния представляется в виде (рис. 1).

Как видно из графика, скорость частицы очень быстро растет на первом этапе взаимодействия взрывной волны с порошковой насадкой, что обусловлено высокой плотностью продуктов детонации в начале их расширения в воздухе (~ 2·103 кг/м3) и высокой начальной массовой скоростью. Дальнейшее снижение темпов роста скорости частицы связано с тем, что уже через время ~ 10-7 с скорость движения частицы порошка становится соизмеримой с массовой скоростью продуктов детонации, которая достаточно быстро спадает с ростом расстояния от центра сферического заряда ВВ. Это свидетельствует о том, что на этом этапе взаимодействия частицы порошка с детонационной волной разрежения происходит «увлечение» частицы молекулами ПД.

Для сравнения динамики частиц порошка и молекул продуктов детонации, расширяющихся в окружающее пространство, используя данные работ [4,5], представим графическую зависимость массовой скорости от расстояния до центра заряда взрывчатого вещества (рис. 2). При построении зависимости u = u(r) использовался сферический заряд гексогена радиусом 2 см и массой 120 г. Как показывает анализ, основной рост скорости движения частицы порошка происходит при давлении во фронте волны разрежения больше давления сопряжения [5], поэтому используется только скорость, определяемая соотношением (2).

Для расчета количества теплоты (3), (4) были использованы данные о скорости движения частицы, полученные в работе [4] , а массовая скорость продуктов детонации определялась соотношением (2). Суммирование в соотношении (4) производилось численными методами в системе MathCAD. Зависимость количества теплоты, полученного частицей при ее движении во фронте детонационной волны разрежения, от количества соударений представлена на графике (рис. 2) в двойном логарифмическом масштабе.

В логарифмическом масштабе зависимость количества теплоты, поглощенного частицей порошка, от числа столкновений практически линейная. При количестве столкновений ~ 1012

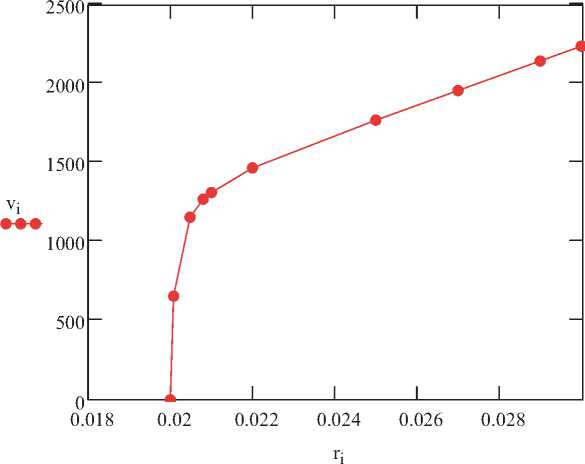
Рис. 1. Зависимость скорости движения частиц порошка от расстояния

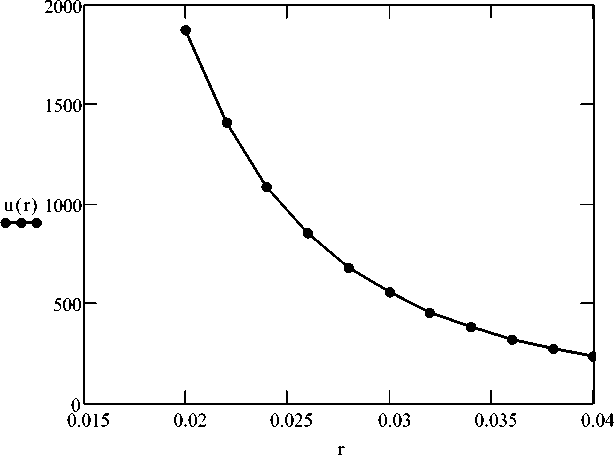
Рис. 2. Зависимость массовой скорости ПД от расстояния

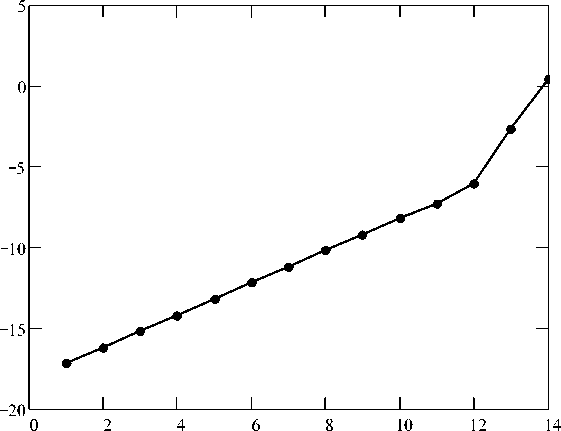
log ( N i )

Рис. 3. Зависимость количества теплоты от числа соударений частицы с молекулами ПД

наблюдается изменение характера зависимости логарифма Q от логарифма N. Это свидетельствует об увеличении скорости роста поглощенной теплоты.

Взаимодействие частицы порошка с молекулами продуктов детонации взрывчатого вещества приводит к ее нагреванию. Важно знать до какой температуры может разогреться частица и достаточно ли теплоты, полученной при соударении для ее плавления. Агрегатное состояние частицы порошка имеет существенное значение для ее дальнейшего взаимодействия с обрабатываемой поверхностью металла или сплава. Поэтому оценим изменение температуры частицы порошка при ее движении во фронте волны разрежения продуктов детонации. Расчеты проводились для порошка бора с размером частиц 5

мкм и массой 1,5·10-13 кг. Изменение температуры частицы определялось соотношением:

Q лт :.v

где c – удельная теплоемкость бора; M – масса частицы бора; Q – количество теплоты, определяемое соотношением (4). Зависимость изменения температуры частицы от количества соударений в двойном логарифмическом масштабе представлена графически на рис. 4.

Как видно из графика в логарифмическом масштабе зависимость ∆T от числа соударений растет линейно и при N~ 1012 скорость роста температуры увеличивается. Так как температура плавления бора ~ 2200 К, то, как видно из графика, частица порошка может быть нагрета до температуры плавления .

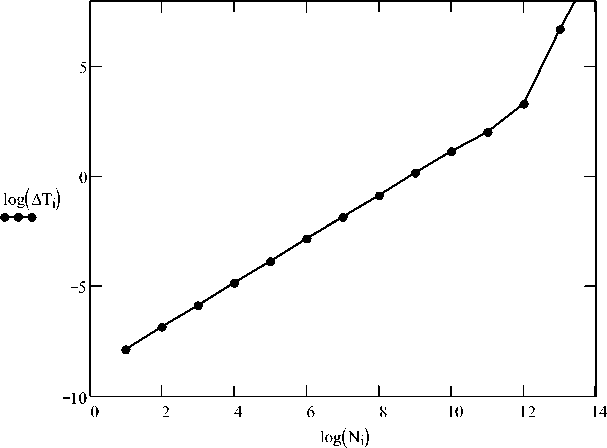
Рис. 4. Зависимость изменения температуры от числа столкновений

Если говорить конкретно о взрывном распылении порошка бора, то температура частиц бора важна еще и с точки зрения химического взаимодействия бора с продуктами детонации взрывчатого вещества. При температуре выше 1500 К бор вступает в химическую реакцию с азотом с образованием нитрида бора BN и углеродом с образованием карбида B4C. В большинстве взрывчатых веществ эти элементы присутствуют и в результате взрывных химических превращений могут содержаться в продуктах детонации, взаимодействующих с частицами бора.

Таким образом, процесс нанесения износостойких и упрочняющих покрытий на металлы и сплавы методом взрывного напыления очень чувствителен к динамике и термодинамике частиц порошка. Изменяя характеристики взрывчатого вещества, конструктивные особенности взрывной камеры и порошковой насадки можно управлять процессом напыления и создавать покрытия необходимой структуры.