Энергетический подход к вычислению магнитных сил, действующих на твёрдые тела в феррожидкости

Плавание твёрдых тел в магнитных коллоидах — феррожидкостях (ФЖ), изучается со второй половины 60-х годов прошлого века. Первые работы в этой области [1–3] посвящены уникальному явлению левитации постоянного магнита, погружённого в контейнер с ФЖ. Плавание магнита плотностью p_s6 в ФЖ с меньшей плотностью р_# <  р_$6 происходит благодаря отталкиванию его полюсов от стенок контейнера, являющихся границей раздела магнитной и немагнитной сред. В работах [2, 3] сформулирован подход к описанию сил, действующих на погружённые в ФЖ тела, который без существенных изменений используется по настоящее время, а именно: сила вычисляется как интеграл по поверхности тела от давления, определяемого в соответствии с уравнением Бернулли для ФЖ [1, 4].

Итак, если в точке с координатами ( r, ф , z ) напряжённость магнитного поля равна H , то давление в этой точке составляет:

H p = p 0 -P#g ( z - z 0 ) + Цо JM (Hi) dHi, 0

где p₀ = p ( r , ф₀, z ₀) — постоянное давление в некоторой контрольной точке (например, атмосферное давление на плоскую горизонтальную поверхность ФЖ), g = ( 0,0, - g ) — вектор ускорения свободного падения, ц₀ = 4 п- 10 7 Гн/м — магнитная постоянная, индекс i обозначает переменную интегрирования, M ( H ) — нелинейная зависимость намагниченности коллоида M от напряжённости магнитного поля. Кривая намагничивания феррожидкости M ( H ) измеряется экспериментально и является её паспортной характеристикой. Помимо давления (1), необходимо учесть специфический для ФЖ скачок магнитного давления на поверхности тела (границе раздела сред). Таким образом, окончательное выражение для силы, действующей на тело в намагниченной ФЖ, имеет вид [4]:

F = mb g - фpndS - Ц ф (M2 /2) ndS = - (рsb -Pf ) Vsbg - F, - F„ ,(2)

SS

F = цф(HM(H)dH)ndS ,(3)

F„  - ф(M2/2)ndS ,(4)

S где Vsb — объём тела, n — вектор нормали к поверхности тела, Mn = Mn — нормальная компонента намагниченности. В выражении (2) первое слагаемое является Архимедовой силой, а слагаемые F и F — пондеромоторные силы, которые вносят определённую трудность в аналитические исследования, так как выражаются через интегралы от сложной нелинейной и многопараметрической функции, индивидуальной для каждого образца ФЖ. Конкретная кривая намагничивания зависит от дисперсного состава коллоида [5, 6], то есть от параметров распределения коллоидных частиц по размерам, и от объёмной доли магнитной фазы ф (концентрации магнитных наночастиц). В силу того, что выражения (1)–(4) получены на три десятилетия раньше точной теории магнитогранулометрического анализа полидисперсных ФЖ [5, 6], корректное описание процесса намагничивания M (H) заменялось (с целью упрощения) рассмотрением двух предельных случаев — слабого и сильного — магнитного поля, о величине которого можно судить по соответствующему безразмерному числу — параметру Ланжевена:

^ = Ц mH (kkbT), являющемуся отношением магнитной энергии коллоидной частицы со средним магнитным моментом m к её тепловой энергии kT, где k — постоянная Больцмана, а T — абсолютная температура. В случае типовых феррожидкостей вида «магнетит–олеиновая кислота–керосин», полученных стандартным методом химического осаждения [4], средний магнитный момент частицы равен m ~10-19 А^м2, следовательно, магнитное поле считается слабым ( ?<< 1) при значениях H ~102 А/м и сильным (^>> 1) при H ~105 А/м. Оба эти приближения неудовлетворительно описывают реальные лабораторные эксперименты, так как характерные магнитные поля, получаемые в лабораторных условиях с помощью соленоидов и постоянных магнитов, составляют H ~104 А/м. Тем не менее, два грубых упрощающих приближения слабого и сильного поля используются до сих пор потому, что позволяют заменить сложный нелинейный закон намагничивания M (H) на линейную функцию с одним параметром, известным из экспериментальных измерений:

M =X q H ,     ц= 1 + % 0 >> 1    при ^<< 1,

M=Ms,    ц =1 + х® 1     при ^>> 1, где Хо — начальная магнитная восприимчивость, ц — магнитная проницаемость, Ms — намагниченность насыщения ФЖ, х — магнитная восприимчивость жидкости. Оба приближения основаны на упрощающем допущении х = const ■ Такой подход делает возможным получение простых аналитических выражений для сил (см. (3), (4)) и количественной оценки порядка их величины.

Дальнейшее развитие идей из пионерских работ [2, 3] продолжилось в [7–10]. Работы [7, 8] предлагают аналитическое решение задачи в необычной (не встречающейся на практике) постановке: цилиндрический магнит, намагниченный поперек своей главной оси, левитирует в горизонтальной цилиндрической полости, заполненной ФЖ с линейным законом намагничивания ( M =%₀ H ). Эта же задача в безындукционном приближении решена в [9]. Безындукционное приближение (non-inductive approach) — это очень популярный упрощённый подход к вычислению магнитных полей и сил в ФЖ, подразумевающий, что х<< 1 и Ц~ 1. Такое упрощающее приближение оправдано в двух случаях: во-первых, уже упомянутых сильных внешних магнитных полях Н_о, намагничивающих ФЖ до насыщения ( M ® M_s , х<< 1, Ц® 1); во-вторых, в слабоконцентрированных ФЖ ( ф<< 1, % = M/H << 1, ц® 1), применяющихся на практике в биомедицине. Первый случай с оговорками применим к задаче левитации постоянного магнита в ФЖ. Так, в [9] приводится оценка точности безындукционного приближения, где показано, что приближённое решение [9] удовлетворительно согласуется с точным [7, 8] только при условии х< 0,25 ■ Если же, например, % = 1, то отличие безындукционного и точного решений составляет 20%, а при х= 1,5 расхождение превышает 30%, и оно далее монотонно возрастает с увеличением % .

Следует также подчеркнуть, что в случае немагнитных тел, погружённых в ФЖ, безындукционное приближение не только даёт количественно неточный результат, но и концептуально противоречит самой постановке задачи. Действительно, размагничивающее поле H ФЖ, помещённой в однородное внешнее магнитное поле H ,— это единственная причина возникновения сил левитации, а безындукционное приближение подразумевает парадоксальное пренебрежение этим размагничивающим полем ФЖ на том основании, что H df <<  H o .

Аналитические исследования 2000-х годов [11, 12] предлагают точное решение уравнения Лапласа для магнитного поля в задаче плавания сферического магнита или парамагнитного тела внутри сферического контейнера, заполненного ФЖ, при наличии внешнего однородного магнитного поля H . В рамках безындукционного приближения результаты [11, 12], полученные для задачи со сферической симметрией, обобщены на случай эллипсоидальной формы контейнера и рассмотрены для двух предельных случаев (бесконечный цилиндр и бесконечный плоский слой), а также предложены приближённые формулы для сил, действующих на плавающее тело. Эти результаты являются существенными, но допускают количественное сравнение с реальным лабораторным экспериментом только тогда, когда условия эксперимента удовлетворяют условиям безындукционного приближения. В дальнейшем авторы [11, 12] проделали цикл работ, посвящённых различным принципам создания механического движения тел посредством переменных магнитных полей (см., например, [13]). Эти работы выполнены с учётом безындукционного приближения и носят прикладной, а не фундаментальный характер. Существует множество других современных работ (см., например, обзоры [14, 15]), связанных с проблемой плавания твёрдых тел в магнитожидкостных устройствах (акселерометрах, датчиках угла наклона, дифференциальных манометрах, сепараторах). Однако, несмотря на множество примеров приложения, во всех названных работах авторы не предлагают ничего нового с точки зрения фундаментальной науки и используют приближенные выражения, полученные ещё в 1960-80 гг. Иначе говоря, единственный на сегодня правильный способ вычисления сил, действующих на погружённые в ФЖ тела, — это численное решение системы уравнений Максвелла с привлечением материального уравнения M ( H ) и подстановкой найденных числовых значений полей B , H в уравнения (2)-(4).

Вычисления, производимые по формулам (2)–(4), требуют, как правило, преодоления ряда трудностей, связанных с определением полей B , H непосредственно на границе раздела «твёрдое тело–ФЖ». Проблемы возникают потому, что открытые программные пакеты решают магнитостатическую задачу методом конечных элементов для векторного потенциала A :

rot I —— rot A I = J , (6) )

где J — вектор плотности электрического тока, и, в силу известной особенности используемого метода, операция дифференцирования B = rot A на границе раздела двух сред приводит к большой погрешности вычислений. Эту трудность обычно предлагается обойти следующим образом [16, 17]: проводить расчёты не по поверхности тела, а по вспомогательной виртуальной поверхности (eggshell), расположенной от настоящей на некотором расстоянии, превышающем минимум суммы нескольких характерных размеров расчётной сетки, а порой (при автоматическом выборе, осуществляемом в открытом программном пакете) это расстояние может быть сопоставимым с характерным размером тела. Справедливость такого подхода математически обоснована для окружающей среды с постоянной магнитной проницаемостью ( ц=const). Здесь сила, найденная непосредственно для поверхности тела, точно равна силе, рассчитанной по виртуальной поверхности, располагающейся снаружи на произвольном удалении от тела (при этом размер применяемой сетки не важен, так как этот результат является аналитическим и обусловлен свойствами максвелловского тензора). Однако, как заметно из ограничения ц=const, этот подход не допустим в случае тела, погружённого в ФЖ, ведь в его окрестности неоднородное поле H в разной степени намагничивает ФЖ, и, следовательно, ц не постоянна. Эту проблему, обыкновенно, обходят следующим образом: истинные значения интегралов (3), (4) находят экстраполяцией после их многократного вычисления по вложенным виртуальным поверхностям, близко расположенным как друг к другу, так и к исследуемому телу [18, 19].

Но возможен и альтернативный энергетический подход к решению подобных задач, лишённый указанных трудностей и недостатков. Назовём его основные очевидные преимущества. Во-первых, энергия тела рассматривается как интеграл по его объёму, и поэтому точность её расчёта менее подвержена упомянутым ранее ошибкам, связанным с разрывом функций B , H на поверхности тела. Во-вторых, электромагнитная энергия в программных пакетах реализована в виде готовых функций, использование которых намного проще, чем формул (3), (4), так как последние зависят от формы тела.

В случае энергетического подхода сила, действующая на погружённое тело, записывается как градиент потенциальной магнитной энергии W :

F = - grad W.(7)

Результат вычислений (7) зависит от двух принципиально важных обстоятельств.

Первое обстоятельство заключается в том, что существует два разных способа отыскания W [20]:

f B^

W =J| Jh(B)dB IdV ,(8)

• V ^ 0

f H^

Wcoe = ЩB (H) dHI dV .(9)

• v V 0

2.    Практическая часть

Здесь W — это энергия (energy) магнитного поля. Величина W в отечественной литературе не получила самостоятельного названия, а в иностранной иногда упоминается как «coenergy». При этом внутренняя — U , и свободная — F , энергии тела, определённые посредством (8) или (9), имеют разный физический смысл. Так, изменение термодинамических потенциалов с dW (8) представляет собой работу, совершённую магнитным полем над системой при постоянных потенциалах магнитного поля, то есть когда поле в лабораторном эксперименте создаётся сверхпроводящими магнитами. В свою очередь изменение dU или dF , вычисляемых через dW (9), задаёт работу, совершённую над системой при постоянных источниках магнитного поля, то есть когда поле в лабораторном эксперименте создаётся постоянными токами (соленоидами и электромагнитами, подключёнными к источникам электрического тока). Второй вариант встречается в лабораторных исследованиях значительно чаще первого, поэтому многие авторы без пояснений предлагают представлять (7) в виде

F = - grad W_coe .                                           (10)

Подчеркнем, что описанные ранее упрощения (5) принципиально не позволяют сделать различие между (8) и (9), так как для линейной системы поле B прямо пропорционально полю H , поэтому BdH = HdB. Это значит, что численная проверка (7) с различными значениями (8), (9) имеет определённый самостоятельный смысл. Этому вопросу в настоящей работе уделено отдельное внимание.

Второе обстоятельство, касающееся применимости энергетического подхода к описанию сил и его эквивалентности (2)–(4), заключается в установлении границ пространства V , по которому необходимо интегрировать в выражениях (8), (9).

Подводя итог вводной части, сформулируем цель предлагаемого исследования: с помощью прямых вычислений требуется ответить на вопрос о том, какой из двух термодинамических потенциалов — (8) или (9), и какую область пространства V следует брать за основу при энергетическом подходе к нахождению магнитных сил (2)–(4), реально измеряемых в лабораторном эксперименте.

Для точного ответа на поставленные вопросы необходимо сравнить магнитные силы, вычисленные по формулам (2)–(4), с двумя значениями (7), полученными с помощью энергетических подходов (8) и (9),

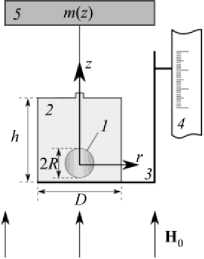
Рис. 1. Схема лабораторного эксперимента [21]: 1 – оловянный шар на подвесе; 2 – кювета с феррожидкостью; 3 – подвижная вдоль оси z горизонтальная платформа; 4 – катетометр; 5 – аналитические весы

и сопоставить все численные результаты с результатами лабораторного эксперимента [21], выполненного с той же целью — исследовать силы, действующие на немагнитное тело, погружённое в ФЖ.

Эксперимент [21] заключался в определении электромагнитных сил по изменению веса тела, погружённого в кювету с ФЖ. В отсутствие поля H вес тела обуславливается только силой тяжести и Архимедовой выталкивающей силой. При включении внешнего поля H к равнодействующей силе добавляется магнитная составляющая, и первоначальный вес тела изменяется. Это изменение веса и является искомой электромагнитной силой.

Геометрия и условия вычислительной задачи в точности соответствовали параметрам лабораторной установки [21], изображенной на рисунке 1: оловянный шарик 1 радиуса R = 3,79 мм погружался на подвесе в стеклянную цилиндрическую кювету диаметром  D = 26,7 мм  и высотой  h = 13,65 мм, заполненную магнитной жидкостью 2. Кювета с шариком устанавливалась на плоскую горизонтальную платформу 3, при помощи штанги жёстко закреплённую на колонне катетометра 4, но подвижную в вертикальном направлении. Положение платформы с кюветой внутри соленоида плавно регулировалось по высоте. Таким образом, подвижная платформа обеспечивала вертикальное смещение кюветы с ФЖ относительно шарика, покоящегося на проволочном подвесе. Вес немагнитного шарика измерялся высокоточными аналитическими весами 5. Величина магнитной силы, действующей на шарик при его смещении относительно центра кюветы, определялась по значению разности его веса в данной точке в условиях действующего на него магнитного поля и в нулевом поле ^m (z) - m0 (z)J g. В центре кюветы вес пробного тела не меняется при любом значении напряжённости внешнего поля m (0) g = m0 (0) g , так как в этом случае верхняя и нижняя крышки (границы раздела сред) оказывают на шар воздействие, одинаковое по модулю и противоположное по направлению.

Соответствующая эксперименту [21] магнитостатическая задача решалась численно в осесимметричной постановке, в цилиндрических координатах. Расчётная область содержала сферическое тело в центре области, цилиндрическую кювету с ФЖ и соленоид, питаемый источником постоянного тока. Размеры всех объектов ( R , D , h ), а также размеры соленоида были взяты из эксперимента. В силу цилиндрической симметрии трехмерная (3D) задача допускала упрощение до двумерной (2D) постановки, что позволило решить её численно с использованием открытого программного пакета FEMM, возможности которого ограничиваются плоскими и осесимметричными 2D задачами.

Граница расчётной области состояла из вертикальной линии, совпадающей с осью симметрии задачи (осью z цилиндрических координат), и полукруглой дугой радиуса R ® 30 h . На полукруглой границе были заданы открытые, а на вертикальной линии — симметричные граничные условия [22] для векторного потенциала A .

Выражения (3) и (4), естественно, не существуют в виде встроенных в пакет FEMM функций, поэтому предварительно они были записаны в виде аналитических выражений с учётом сферической поверхности твёрдого тела. После небольших аналитических преобразований z - компоненты сил (3) и (4) приобрели вид:

F„ = 2 п_{И о} R¹

j

H ( r , z )

J M (H (r, z)) dH (r, z)

cos ( 0 ) sin ( 0 ) d 0 e_z ,

F„ = n a R ¹}" M 22 ( r , z ) cos ( 0 ) sin ( 0 ) d 0 | e_z, Uo                   )

r = R sin ( 0 ) , z = - R cos ( 0 ) ,

M n = M_r sin ( 0 ) + M_z ( - cos ( 0 ) ) ,

где 0 — полярный угол. Вычисления по (11) проводились с учётом реальных физических свойств материалов. Кривая намагничивания M ( H ) (Рис. 2), измеренная экспериментально, загружалась в FEMM в табличном виде B ( H ) = ц₀ ( M ( H ) + H ) .

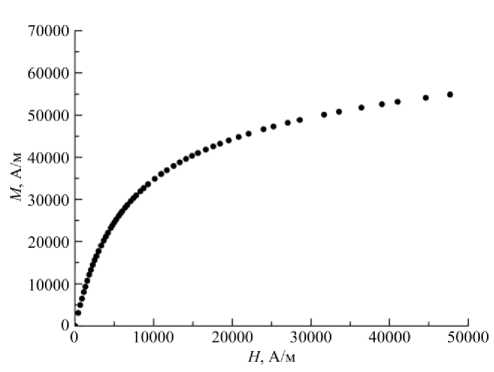
Рис. 2. Экспериментальная кривая намагничивания M ( H ) феррожидкости, использовавшаяся в вычислениях

Непосредственно программа для FEMM представляла собой скрипт на языке Lua, содержащий последовательное описание геометрии задачи, физических свойств материалов, начальные условия и основной вычислительный цикл. Начальные условия подразумевали, что кювета с ФЖ располагается в наивысшей точке (когда оловянный шарик касается её дна). Вычислительный цикл содержал последовательность действий: очистку расчётной сетки, созданной в предыдущем цикле; параллельное смещение кюветы с ФЖ вниз по оси z на 0,1 мм (при этом шарик считался неподвижным); формирование новой сетки; определение значений поверхностных интегралов (3), (4) для пяти концентрических сферических поверхностей с радиусами

Rk = R + kdR (k = 1,..., 5), где приращение dR равнялось полуторному размеру шага расчётной сетки. Полученные значения для сил (3), (4) записывались в файл, и далее основной вычислительный цикл продолжался до тех пор, пока центр кюветы с ФЖ не опускался ниже начала координат. Необходимость многократного вычисления интегралов (11) для экстраполяции их истинных значений пояснялась во введении.

Второй этап программы повторял геометрию задачи, но определялись не силы (11), а значения магнитной энергии в виде (8) и (9) для каждой области пространства по отдельности (для твёрдого тела, ФЖ, окружающего воздуха). При этом выражения (8) и (9) существуют в FEMM в виде встроенных функций, что является значительным преимуществом, ведь простота выражений (11) объясняется лишь сферической геометрией немагнитного тела. Вычисленные в точках значения энергий W_e ( z ) , W_co Д z ) с интервалом 0,1 мм интерполировались соответствующими полиномами в Wolfram Mathematica, после чего дифференцировались там же в соответствии с (7). Полученные таким образом силы F ( z ) сравнивались с рассчитанными по формулам (11) и с данными экспериментальных измерений [21].

Отдельно отметим, что для достижения цели исследования численное моделирование проводилось для нескольких значений напряжённости внешнего магнитного поля H , при этом отслеживалось, чтобы для моделируемого образца ФЖ с заданным законом намагничивания M ( H ) заведомо не выполнялись ни условия (5), ни безындукционное приближение.

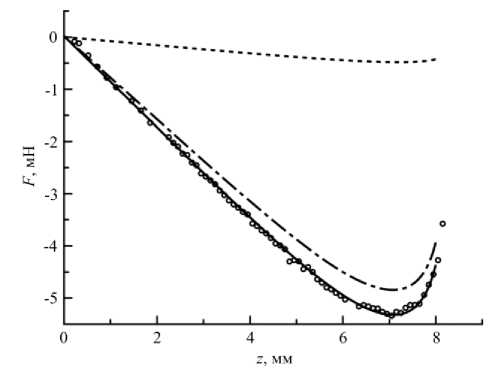
Рис. 3. Магнитная сила, действующая на оловянный шарик в ФЖ при Н _о= 20 кА/м: точки - эксперимент [21], штриховая линия -

сила F , штрихпунктирная линия – сила F , сплошная линия –

равнодействующая сил F и F

3.    Результаты вычислений

Результаты расчётов, выполненных для значения внешнего поля Н _о = 20 кА/м, представлены на рисунках 3, 4. На первом этапе (Рис. 3) осуществлялась проверка формул прямого определения электромагнитных сил (3), (4). Результаты, приведённые на рисунке 3, важны по двум причинам. Во-первых, эти данные показывают хорошую точность формул (3) и (4), достаточную для описания экспериментальных измерений. Во-вторых, прекрасное совпадение расчётной и экспериментально измеренной сил подтверждает корректность расчёта магнитного поля, ведь в формулы (3), (4) непосредственно входят значения напряжённости H и индукции B .

После того как на первом этапе было получено подтверждение правильности расчёта магнитного поля в пакете FEMM, далее был проведён расчёт этих же магнитных сил, но уже в рамках энергетического подхода (7). С этой целью для трёх расчётных областей пространства (оловянного шарика, цилиндрической кюветы с ФЖ и окружающего воздуха) вычислялись энергии W и W по формулам (8) и (9) соответственно. При этом для объёма шарика и окружающего воздуха имело место равенство: W_e = W_coe , потому что эти среды являются парамагнетиками с постоянными ц . Для объёма ФЖ W_e ^ W_coе, и этот факт определяет отличие кривых на рисунках 4 а , б .

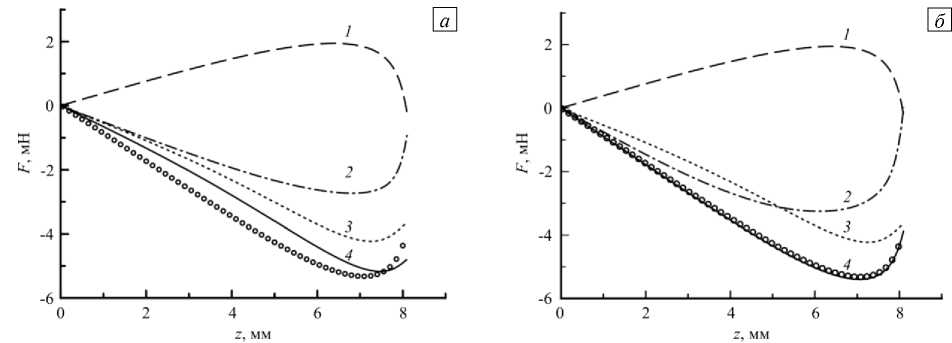
Рис. 4. Магнитные силы при наличии внешнего поля Н_о = 20 кА/м, вычисленные через градиент W_e по формулам (7), (8) ( а ) и через градиент W по формулам (7), (9) ( б ), для оловянного шарика (кривые 1 ), объёма ФЖ ( 2 ), воздуха, окружающего кювету с ФЖ ( 3 ); равнодействующая сила ( 4 ); символами обозначена равнодействующая сила, рассчитанная по формулам (3), (4)

Таким образом, для каждой напряжённости внешнего магнитного поля H вычислялось три значения (8) и одно значение (9), после чего таблицы значений W ( z ) обрабатывались в Wolfram Mathematica по алгоритму, описанному в предыдущем разделе. Результатом обработки исходных данных W ( z ) были функции F ( z ) , аналогичные показанным на рисунке Рис. 4. Как видно из графиков, только применение W_coе ( z ) для всей расчётной области позволяет корректно описать действующие силы (кривая 4 на Рис. 4 б) . Этот результат, с одной стороны, является закономерным, так как по условию задачи магнитное поле создавалось не сверхпроводящими магнитами, а соленоидом с постоянным током, и поэтому термодинамические потенциалы внутренней ( U ) и свободной ( F ) энергий следует находить через W . С другой стороны, необходимость учёта всей области пространства является в некоторой мере неожиданным результатом. Так, в начале исследования в качестве основного высказывалось предположение, что магнитная сила, действующая на немагнитное тело и реально измеряемая в лабораторном эксперименте, определяется энергией (9) самого тела, то есть предполагалось, что интеграл (9) необходимо вычислять только по объёму тела (оловянного шарика). Однако численный результат показал, что необходимо рассматривать всю систему «твёрдое тело–ФЖ–воздух», взаимодействующую посредством электромагнитных сил. При этом перемещение твёрдого тела приводит к изменению магнитного поля не только в нём самом, но также и в ФЖ, и в окружающем пространстве, что в свою очередь (в силу третьего закона Ньютона) оказывает обратное воздействие на тело. Это воздействие имеет магнитную природу, но проявляется в виде механической силы, которую можно измерить аналитическими весами в лабораторном эксперименте.

4.    Заключение

В настоящей статье приводится подробный обзор работ, посвящённых изучению сил, действующих на твёрдые тела, погружённые в намагниченную феррожидкость. Обзор литературы убедительно показывает необходимость и потенциальное преимущество использования энергетического подхода в подобных задачах, так как аналитические выражения для сил (3), (4) существенно зависят от формы тела, а получение конечного численного результата с использованием (3), (4) осложняется значительной погрешностью расчёта полей H , B непосредственно на границе «твёрдое тело–ФЖ», так как нормальная компонента H и тангенциальная компонента B в этом месте терпят разрыв. Энергетический подход, наоборот, позволяет использовать стандартные функции программных пакетов для нахождения термодинамических потенциалов (8) и (9). Отличие между (8) и (9) определяется постановкой задачи и может быть выявлено только для среды с нелинейным законом намагничивания, что ранее не проводилось ни экспериментально, ни теоретически ввиду повсеместного использования упрощающих предположений (приближения слабого и сильного магнитного поля, безындукционного приближения).

Для обоснования энергетического подхода к отысканию сил, действующих на немагнитные тела в ФЖ, было выполнено парное сравнение равнодействующих магнитных сил, рассчитанных по формулам (2)–(4) и по (7) для (8) и (9) соответственно. Результаты вычислений сравнивались с результатами лабораторного эксперимента [21]. Расчёт повторялся для нескольких значений внешнего поля (15, 25 и 30 кА/м); все полученные при этом результаты были аналогичными представленным на рисунке 4.

Проведенные исследования показали, что магнитная сила, действующая на тело, погружённое в ФЖ, определяется энергией (9) всей системы «твёрдое тело–ФЖ–окружающий воздух», а не только лишь одного твёрдого тела. Объяснение состоит в том, что перемещение твёрдого тела приводит к изменению магнитного поля не только в самом теле, но также и в ФЖ, и в окружающем воздушном пространстве, что в свою очередь (в силу третьего закона Ньютона) оказывает равное по величине и обратное по направлению воздействие на тело. Эта механическая сила имеет магнитную природу и является величиной, реально измеряемой в лабораторном эксперименте.