Энергетическое произведение в модели трещиноподобного дефекта при нагружении типа моды II

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2019PNRPU MECHANICS BULLETIN

Классическая постановка задачи о трещине моды II рассматривает бесконечное линейно-упругое пространство с дефектом в виде математического разреза, поверхности которого нагружены противоположными векторами напряжений [1, 2]. В этом случае на продолжении математического разреза в слое нулевой толщины реализуются только сдвиговые напряжения. Для образцов конечных размеров предлагается ряд схем нагружения [3–6], в которых на продолжении трещины реализуется напряженное состояние, соответствующее поперечному сдвигу. Данные схемы также принято рассматривать как трещину моды II. Отметим, что для образцов конечных размеров общие решения строятся, как правило, на основе численных процедур, основанных на методе конечных элементов [7–12]. Аналитические решения получаются, как правило, в рамках упрощающих гипотез [13–19]. Так, в работе [6] для консоли с центральной трещиной на основе гипотез теории пластин Тимошенко получено решение задачи и определено значение J-интеграла. В этом случае в консолях учитывались деформации растяжения и сдвига. Влияние обжатия консолей в результате внешнего воздействия не рассматривалось.

Альтернативной моделью трещины в виде математического разреза является разрез физический с характерной толщиной δ₀ . В данном представлении особую роль играет описание взаимодействия материального объема, лежащего на продолжении физического разреза, со смежной средой. Важно, чтобы та или иная модель не приводила к сингулярности в области окончания физического разреза. При нагружении трещиноподобного дефекта нормальным отрывом отметим модель в виде связей Прандтля, предложенную в статье [20] и используемую в работах [21–23]. В модели Ф. Макклинтока [24] предложено использовать для материала слоя усредненные характеристики напряженно-деформированного состояния (НДС). Постановки конкретных задач исходя из представления Ф. Макклинтока были реализованы на основе теории слоя взаимодействия в работах [18–20], [26–28]. В частности, в статье [27] введено понятие энергетического произведения (ЭП) в виде произведения приращения удельной свободной энергии в элементе слоя и толщины слоя. В статье [18] о нагружении двухконсольной балки (ДКБ-образца) нормальным отрывом (нагружение по моде I) показано, что при уменьшении отношения толщины слоя к высоте консоли имеет место сходимость ЭП к поверхностной энергии, рассчитанной через вязкость разрушения K_IC .

В данной работе предложена схема нагружения ДКБ-образца в которой реализуется состояние, близкое к моде II. На основе общей вариационной постановки задачи [26–28] получены упрощенные постановки с учетом и без учета обжатия консолей. Из аналитических решений показано, что при уменьшении отношения толщины слоя к толщине консоли имеет место сходимость ЭП в слое для данного вида нагружения.

1. Постановка задачи

1 O.55 o ^CT 22 ( x i ) =T" J ^CT 22 ( ⁵ 0 -O.55 o

1 O.55 o ^ct 11 ( ^x i ) =^- J ^CT ii (• ⁵ 0 -O.55 o

x , , x 2 ) dx 2 ,

x , , x 2 ) dx 2 ,

u + ( x _i ) - ^u 2 ( x _i )

5 o

,

Рассмотрим случай нагружения ДКБ-образца согласно схеме, показанной на рис. 1. Правые торцы консолей 1 и 2 образца свободны от внешней нагрузки. Верхняя граница консоли 1 и нижняя граница консоли 2 закреплены от вертикальных перемещений. На левых торцах консолей действует горизонтальная антисимметричная нагрузка интенсивностью P .

r ^{u +(} x i ) ₊ ^{d u -(} x i ) I

^£ ii ⁽ x i ) ^o,5              +              ,

I    d x ,           d x i    J

^Ъ 21 ⁽ x i ) = ^Ъ 12 ⁽ x i ) =

₀ 5 I u i⁺ ( x i ) - ^u i- ( x i )

+ 0,5

d u + ( x _i ) d u 1 ( x _i ) d x ,          d x ,

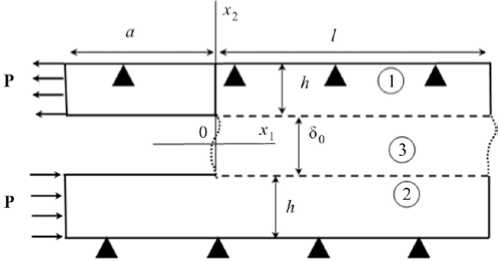
Рис. 1. Схема сдвигового воздействия на тонкий слой

где u ± - компоненты векторов перемещений верхней и нижней границ слоя соответственно; к = 1,2; L , , L 2 -граница приложения внешней нагрузки для тела 1 и 2 . Постулируется жесткое сцепление между границами области 3 и областями 1 , 2 :

u+ = u(x,,50/2);u- = u(x,,-50/2)x, e[0;t],(5)

Примем определяющие соотношения в форме закона Гука:

E L , ^v I

CTy =       I sy +;—^s5ij I,

(i + v)|     i - 2vJ

Fig. 1. Shear effect on a thin layer

Для описания взаимодействия слоя 3 с телами 1 и 2 применим концепцию «слоя взаимодействия», развитую в работах [26–28]. В этом случае условия равновесия тел 1 и 2 запишем в вариационной форме для тела 1 :

J ст ■ -5eds + J ст 225u+dx, + J ct125u+dx1 + s1                   It

I       d5 u+            d5 u +

+ 0,5 5     ст..---- ^- dx . + ct₁₂---- 2-dx = P ^5 u dl (1)

0        11               1          121

It      Эx,       J,      Эx,

где E , v - модуль упругости и коэффициент Пуассона тела; Е - объемное расширение, £ = £ ,, +ъ ₂₂ +£ 33 ; 5 j -символ Кронекера; i , j = 1,1,3.

Для материала слоя взаимодействия 3 определяющие соотношения считаем справедливыми для средних компонент тензоров напряжений и деформаций:

^CT ij

E

1 + v

^£ j - ⁺

v

1 - 2 v

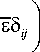
и тела 2

J ст ■ ^5eds - J ct225u2 dx, -J ct125u, dx, + s2                 It

I      d5u-            d5u-

+ 0,5 5    ст..----1- dx + ct₁₂---- 2- dx = P ^5 u dl , (2)

0         11                1          121

It       ax,          •>       ax,

где u – вектор перемещений; P ¹ ,P ² – вектора внешней нагрузки тел 1 и 2 ; S ₁ , S ₂ – площади тел 1 и 2 ; σ , ε – тензоры напряжений и деформаций; σ , ε – тензоры средних напряжений и деформаций слоя с компонентами:

1 O.55 o

^CT 21 ( x i ) =^CT 12 ( x i ) =        J ^CT 21 ( x i , x 2 ) ^d x 2 ,

⁵ 0 -O.55 o

Распределение перемещений в консолях при данном нагружении принимаем в следующем виде:

u(i) (x,, x2) = u, (x,), u 1i)( x,, x 2 ) = Vi (x,)(h + 50/1 - x 2),(8)

u(2) (x,, x2) = u- (x,), u 12) (x,, x 2) = V 2 (x,)(h + 50/1 + x 2).(9)

Вертикальные перемещения тождественно удовлетворяют граничным условиям на верхней границе консоли 1 и нижней границе консоли 2 :

u(i)           = 0, u(1)

¹ x ₂ = h +5 ₀/ 1             ¹ x ₂ =- h -5 ₀/ 1

В этом случае деформацию консолей будут определять компоненты тензора деформаций

^M 12 ⁽ x 1 ) J _— h _—5 y₂ ^O 12 ^{( h + 5} 0/ ^{2 +} x 2 ) ^dx 2 ^{.      (20)}

к             du f ( x 1 ) 8 11 ( x 1 , x 2 ) —       7       , dx 1	(10)
8 22 ( x 1 , x 2 ) — + ^ к ,	(11)
8 12 ( x 1 , x 2 ) — 0,51 dx )( h + 5 0/ 2 + x 2 ) |,	(12)

Интегрируем по частям ряд слагаемых в (13), (14)

с учетом (15)–(20) и четвертое и пятое слагаемые вой части (1) и (2) с учетом (8) и (9):

d 5 u ± ,

¹ dx ₁ dx ₁

—0 dQvv, ± ,

------5 u, dx, , ^adx ₁ ^{1 1}

— I

в ле-

где u ± - горизонтальное перемещение верхней (+) или нижней (-) границы слоя; символ + преобразуется в знак (-) для к — 1, а для к — 2 преобразуется в знак (+).

При распределении деформаций в консолях в виде

f r\k ^{d 5} u 1   7       z-xк e ± | ^x 1 ^{— t}

J o ^Q 11        ^dx 1 ^{— Q} 11 ^{5 u} 1 L -+0

^{j + 0}        dx 1                     ^x 1 ^{—+ 0}

^{— 0} M ^к 2 d* ^adx ₁

dx 1 — M ₁₂ 5v k

—

I x 1 — 0

- —I

(10)–(12) работа внутренних напряжений в теле 1 считывается следующим образом:

рас-

к ^{d 5}V к

dx ₁

,           I x1 —t dx1 — M125V Д, —+0

J a ■■& ds  J J

S 1

X

h +So/2

- a ^M²

I d 5 u + ° 11—-- ° 22 ⁵V 1 ^+O 12

V      dx 1

X

t

^ u— dx 1 — 0 11 5 u^

¹¹ dx ₁

I x 1 —+0

в теле 2:

dx 1 dx ₂ +

r l r ^{h +5}0/²

J +0 ^J5₀/2

^{+ O} 12

J a ■ -5eds — J J s2                     a

dQ^kk^ ±л J +0 _dx ⁵ u ^{1 dx} 1 ,

—

—0 dM 1 ^k 2

^adx ₁

5v _kdx 1 , (23)

+0 M" ⁵V k dx l , ⁽²⁴⁾ dx ₁

I" ^d°ⁿ 5 u ± dx, . (25)

^J +⁰ dx 1      ^{1 1}

I    d 5 u +

°11—--°225V1 + v     dx1

—50/2 I      d 5 u,

—

- h —5o/2

^G11^T dx ₁

dx ₁ dx ₂ ,

1—

--+ 0*22 5^ 2 +

J d ^5v /7,4/4    7 I I 7  7

+ ^Gi2 ------ ( h + 5₀/2 + x ₂)   dx,dx ₂ +

¹² ( dx 1 ^k 0'        ²² )J ^{1 2}

+ р Г—50/2

—

- h —5o/2

I    d 5 u —

^ 11—^ +G 22 ⁵^ 2 ⁺

V      ^dx 1

I ^{d 5}^2 /7,4 I". ,    7 I I 7

+ ^Gn ----- ( h + 5₀/2 + x ₂) dxdx^ .

¹² ( dx1 '        0'        ²² )J ^{1 2}

Введем в рассмотрение обобщенные силы:

Q 11 ( x 1 ) — J o^^2 O 11 dx 2 ,	(15)
n 1 I A _ h+ +50/2     Л Q 22 ( x 1 ) — J 5|)/2    O 22 dx 2,	(16)
Q n ( x 1 ) — J — h — W2 0 11 dx 2 ,	(17)
Q 22 ( x 1 ) — J — h _s 0f 2 O 22 dx 2	(18)

и обобщенные моменты:

1 1 / 7      \ " ⁺⁵0/² _ / 7 . 4               7 7

^M 12 ⁽ x 1 ) ^— J ₅ ^2 ^O12 ^{( h +5}0/² x 2 ) ^dx 2,

. d 5 u ±

12       2

dx ₁

^{— h} I ^O 12 ⁵V k ^ —+0

—

¹¹ = ^{d 5 h} V к , _

O 1           dx, —

+^{0 12} dx 1       ¹

f' ^d °12 4 Л 1

J /⁵ V k d ^x 1 I .

^{J +0} dx J

Рассмотрим правые части уравнений (1) и (2). При положительном обходе контура работа внешних напряжений рассчитывается так:

1                    50/2

J P ■S u dl — — J P 5 u 1⁺ ( — dx ₂ )      —

L 1                      ^{h +5}0/ ²                       x , —— a

— — Ph 5 u+\ x1—— a

6 0/2

J P ² ■S u dl —

L ₁

= — Q15 n-

,

— J P 5 u^ ( — dx 2 ) h +5 0/2

— Ph 5 u —I     — Q 1 5 u —I

¹ x 1 —— a

,

где Q 1 — Ph.

Подставив (13),(15), (16) (21)–(28) в (1) и приравняв

слагаемые при равных вариациях, приходим системам дифференциальных уравнений:

для участка x 1 g [ — a ;0 )

M + Q 12 — 0, dx ₁

do _— о, dx ₁

к двум

для участка x1 e ( 0; t ]

dM ₁ ¹ ₂ dx ₁

1             d o₁₂

+ Q + 0,55_n h -----— h o₂ a ,

22          0                  22

dx ₁

dQLn «=

+ 0,550

dx1

с условиями сопряжения

u 1 U-0    u 1 L=+0 ,	(31)
V 1I X 1=-0 =V 1| X 1=+0 ,	(32)
M 1^1 „=- 0 = ( M 1 + 0,5 6 0 h » 12 ) x =+ 0 ,	(33)
Q 11|   0= ( Q1 1 + 0,5 6 0ЙП )| । X 1 = -0     x                           x i = =+ 0	(34)
и с естественными граничными условиями:
на левом торце
Q hL- .= Q 1 , X 1 = - a	(35)
M 12 I      = 0, 1 X 1 =- a	(36)
на правом торце
( ^1 + 0,5 6 0 ^ 11 )|     = 0, X 1 = t	(37)
( M 12 + 0,5 6 0 h 5 12 )     = 0. '                                       7 1 X 1 = I	(38)
Аналогичным образом из (2) приходим к дифференциальных уравнений:	системам
для участка x 1 e [ - a ;0 )
dM 122     2    dQ 121 ,       Q 22,    ,        0, dx1           dx1	(39)
для участка x 1 e ( 0; / ]
dM 12   z-,2 a     , d 5 12            a Q^ + 0,56n h     + h Caa = 0, 22          0                  22 dx 1                    dx 1
dQ ^* + 0,5 6 0 d C 11 = -5 21 , dx1           dx 1	(40)
с условиями сопряжения
u -      = u -      , 1 1 x 1 =-0       1 1 x 1 =+0	(41)
V 2| X 1 =-0 =V 2| X 1 =+0 ,	(42)

правом торце

( Q i ² i + O,5 6 o 5_u )|     = 0,               (47)

X 1 = ■c

( M 2 + 0,5 6 ₀ h 5 ₁₂ )|    = 0.            (48)

X j = £

С учетом выражений (10)–(12) и условием плоской деформации ( e ₃₃ = 0) определяющие соотношения (6) запишем в виде

1        du, ± o f 1 = D-Ц- + D1V k , dx 1	(49)
/                 du ± c k 2 = + D V k + D 1 --^, dx 1	(50)
5 ^ 2 = L I d Vl ( h + 6 0/ 2 + X 2 ) |, 1 dX ,                          1	(51)

E (1 - v)             Ev            E д       (1 + v)(1 - 2v);      (1 + v)(1 - 2v);     2 (1 + v)

Из (7)–(9), (3) и (4) получим связь средних напряжений в слое взаимодействия с его граничными перемещениями:

- Dd(u++ u1L D11(      \z„x

^11 =—  -----+ — h (V1 -V 2),

2     dx16

D ,        , D 1 d ( u + + U 1 )

C 22 =s h ( V 1 V 2 )+ ,      ,       ,       (53) 6 0                 2       dX 1

т ( u + ^{- u}- , a c J ^d V 1 , d V 2 D = L --+ 0,5 h I--1--I .

( ⁶ 0           ( dX     ^dx 1 ))

Таким образом, система дифференциальных уравнений (29), (30), (39), (40) с учетом связей (10)–(12), (15)–(20) и определяющих соотношений (49)–(54) является замкнутой относительно четырех неизвестных функций u + , u - , v ₁ , V ₂ . Каждая искомая функция входит в систему со второй производной включительно. Удовлетворение восьми граничных условий (35)–(38), (45)– (48) с учетом сопряжения решений (31)–(34), (41)–(44) даст решение поставленной задачи.

M ’2I „=- 0 = ( M 2 + 0,5 6 0 h 5 12 ) , =, 0 ,	(43)     2. Решение задачи
Q 1>L., = ( Q 21 + 0,5 6 0 5 11 ) 1X 1 = - 0     x                          7 l X 1 =+ 0	Рассмотрим решение поставленной задачи в виде (44)      u + = - u - , v 1 = v 2 для полубесконечного образца ( I ^ «). В этом случае движение консолей противоположно,
и естественными граничными условиями:	с одинаковым модулем обжатия. Для решения задачи
на левом торце	достаточно рассмотреть только систему уравнений (29),
Q 121L- .=- Q 1 , X 1 — - a	(45)    (30) при следующих выражениях обобщенных сил:
M 12|      = 0, 1 X 1 =- a	(46)              Qn ( Xi )= 1? +T 5 11 dX 2 = h | DdT" - D 1V 1 |,    (55) ( u)                                     J60/2                    1      dX 1               1

1 /   \     h^{+ +}§0/2      ,       . ।                    ^d u ¹

^Q 22 ( x 1 ) = J ₅ ,2   ^G 22 ^dx 2 = ^h\ ^{— D} V 1 ^{+ D 1}T— |,

0/                      v                   d ^x1 )

Рассмотрим решение на участке x e ( 0; / ] . Запишем систему (30) с учетом выражений (55)–(60):

обобщенного момента

V^ K 2 _{V 1} - K 3 <,

1 A    h +⁺§0^²_                              -h³ d V 1

^M 12 ^{( X} 1 )    J _s ,2 ^G 12 ^{( h +} § 0/ ² x 2 ) ^dx 2 в, ,

⁰                                    3    dx ₁

u' 1 = Ku + + K 1 v 1 ,

и средних напряжений в слое

2L где K =-----;

h §₀ D

K 1 = ^ I D ¹;   K 2 =

D

^G 11 = 0,

3 D      ;

-h ² f 1 + 1.5 § 0 ¹

V h J

^ 22 = 0,

³ ( ^- + ^{D 1} )

K 3 =

Lh ²

.

_ — | 2 u +     d Vj | ст. 2 = -1 —- + h —— |.

V § 0       ^dx1 )

Систему линейных дифференциальных уравнений второго порядка (68) сведем к системе линейных дифференциальных уравнений первого порядка:

Проинтегрируем второе уравнение системы с учетом граничного условия (35) и связи (55):

, +  D1     Q u = —Vi +--.

1 D 1 hD

I u^	1	1 0	0	0	1 I	I u + I
V 1		0	0	1	0	V 1
w		0	K 2	0	— K 3	w
V V )		V K	0	K 1	0 )	V v )

.

Запишем первое уравнение системы (29) с учетом (56), (57) в виде

-3- v 1¹ = D V 1 — Dlu l ⁺ .

Из (61), (62) приходим к следующему неоднородному дифференциальному уравнению второго порядка:

V 1 ¹

g 1 2

7 I V i = A, h )

Характеристическое уравнение системы (69) шем в виде

X ⁴ + b X ² + c = 0,

запи-

где b = K 1 K 3 — K 2 — K ; c = KK 2.

Коэффициенты биквадратного уравнения (70) представим в виде

3 ( D ² — D 1 ² ) где g = —-------- >  0; A = —

LD

3 D 1 Q 1 LDh ³ .

m b =--, h §0

Запишем общее решение (63):

gg X -i

V ₁ = C ₁ e ^h + C ₂ e^h

—

D 1 Q 1

h ( D ² — D 1 ² ) .

c =-----7----------\, h3§0| 1 +1,5§0 I

⁰ V , h )

(

A

Из граничного условия (36) и выражения (57) находим связь постоянных интегрирования

m =

1 — 2 v

1 — v

_ 2 ag

C ₁ = C ₂ e ^h

V

6 ( 1 — v )

( 1 — 2 v ) f 1 + 1,5 §

V h

§ 0

1,5        § 0

h   ( 1 — 2 v )( 1 — v ) h .

)

.

Дискриминант уравнения (70) имеет вид

Таким образом, из (64), (65) имеем

(   g ( 2 a + xi )

V 1 = C 2 e

V

h

gX 1 | ⁺ e h

)

—

D 1 Q 1

h ( D ² — D 1 ² ) ,

, I n I d = 1 I

V ^h § 0 )

,

а из (61) и (66) получаем распределение горизонтально-

го перемещения на участке x ₁

e [ — a ;0 ) :

где n = m

—

24     § 0

1 + 1,5 § 0 1 h h J

.

u + = C₂ — e ^{1     2} Dg V

x 1

—

_ g ( 2 a + X 1 ) 1

e h

+

+ Q 1 X 1 ( D² — 2 D ¹² ) + C hD ( D ² — D 1 ² )      ^3.

На рис. 2 приведем зависимость n ² от отношения h /§₀ для различных значений коэффициента Пуассона.

Из приведенных зависимостей видно, что для выбранного коэффициента Пуассона существует пороговое значение отношения h/ 5 ₀, для которого n ² становится положительной величиной. При дальнейшем из-

ложении будем рассматривать только такие толщины слоя и консоли, при которых n ² > 0 . Из (70) в этом случае получаем собственные значения:

mm

Х12 =±   —, Х34 = ±   _,

^1,2      ^ h 5 0     3'4      ^ h 5 0

где т 1 = 0,5 ( m + n ) > 0; m ₂ = 0,5 ( m - n ) > 0.

Запишем решение системы (74) в следующем виде:

S4 =

RR 2 - VR 3

R 4 - V 1 R 3 - R 1 R 2,

S 2 = V - V 1 S 4 ,

C ₂ = R + R 1 S ₄,

C 3 = S 2 + S 4

-

_C D 1 h

² Dg

2 ag

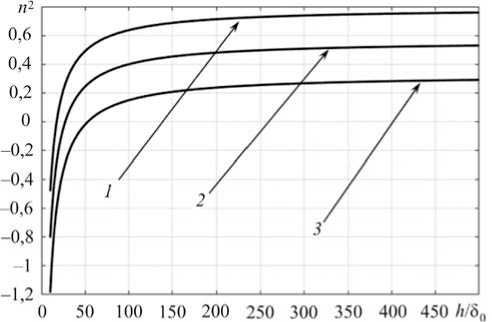
Рис. 2. Зависимость n ² от отношения h /5 0 : ( 1 ) v = 0,1; ( 2 ) v = 0,2; ( 3 ) v = 0,3

где V = , Q _v       V 1 = ( ^{— 1} 4 - ^{— 1} q 4 ) ;

h ( — X ₂ - — 1 q ₂ )              ( — X ₂ - — 1 q ₂ )

- 2 ag

M = 1 + e ^h ;

D 1 Q 1

B ²   h ( — ² - — 1 ² ) ;

_R = Vq 2 + B 2 , M ^;

R1 =

q 4 ^- V ¹ q 2 .

M ;

f h 3   50 h21, x    + -0+

V 32

2 2„ f    - 2ag 1

R 2 = h-g 1 - e ^h ;

3 V J

R4 = q4X4 f h- + 50h-1 + h .

^{4 4} 1 3       2 J

R 3 = q ₂ X ₂ x

Fig. 2. Dependence of СС n ² on ratio h] 5 0 : ( 1 ) v = 0,1; ( 2 ) v = 0,2; ( 3 ) v = 0,3

Рассмотрим упрощенный вариант решения рассмотренной задачи, положив в задании поля перемещений (8), (9) * 1 =* ₂ = 0. В этом случае из (29)-(38) с учетом (58) приходим к следующей постановке задачи:

для участка x 1 е [ - а ;0 )

dQ 1 = 0 dx₁

Запишем решение (69) в следующем виде:

для участка х 1 е ( 0; Z ]

где q j =

4 и + = У S j e j j =1

* 1 = i Sqe ^{X j} j =1

dQ 11 =- dx₁

21 ,

^{2 X} j ^{( 1 -v ) -}

V

(1-2v) 1

^h5 0 ^X J- J

При удовлетворении на бесконечности граничных условий (37), (38) получаем S 1 = S ₃ = 0.

Найдем постоянные C ₂, C ₃ в (66), (67) и S ₂, S ₄ в (72), (73) из условий сопряжения решений (31)–(34):

C — 1 - e ~ h + C = S2 + S4,

^{2 —}g V J ³²⁴

f - g 1       — 1 Q

^{C 2} V ^{1 +} e   Г h ( — 2 - — 1 2 ) = S ² q ^{2 +} S ⁴ q 4 ,

< C2h-gf1 -e~^ 1 = S2fq2X2f— ■ —1 + h 1+ (74)

² 3 V J ² V "2 ² V 3     2 J J

_ f . f h3 50h21 ,)+S4 I q 4X 4 I — + —2— I + h I,

Q = S ₂ ( — X ₂ - — 1 q ₂ ) + S ₄ ( — X ₄ - — 1 q ₄ ) .

с условиями сопряжения u+

¹ X 1 =-0

= ^u 1⁺|

I X ] =+0 ,

I X 1 =-0

I X 1 =+0

и граничным условием в левом торце

Q 11L- д= Q 1

X } —- а

и правом торце

Q 11L , = ⁰, X j £

। 2и. |      1                 dut где -12 = i|—^ I; Q11 (Xi ) = h— -.

i 5 _n J                      dX

В постановке (75)–(80) связь (76) соответствует постановке «дифференциального сдвига», предложенной в [29] и обсуждаемой в [30].

Решение (75)–(80) запишем в виде

u + = Q 1

f

X1         5n

V —h v 2 L—h

u + = - Q 1

I ⁵ 0 e N—h S 0 ^X1 2 LDh

, X 1 е

, X 1 е

[ ^- a ^;0 ) ,

[ 0; ^£ ) .

Введем в рассмотрение энергетическое произведе-

ние (ЭП) [27] среднее на элементе слоя размером

50 х5

2 Y = 5 o ф ,                   (82)

1 5о где ф = — |ф(x)dxx ; ф(x) - средняя удельная сво-5о 0       1' 1

бодная энергия по толщине слоя.

Из (81) находим

2 Y =

(Q )2

2 ^ 2 LDh 5 0

(

e

)

- 1

При 5₀ / h ^ 0 выражение (83) принимает постоянное значение

с учетом обжатия и без него; ё W = — , где u + ^c - гори- ¹² 5 0             ^{1         2}

зонтальное перемещение в модели с обжатием. На рис. 4 построены деформации ё 1 p , p = c , w ,1 c , 2 c в слое с учетом и без учета обжатия консоли, а также слагаемые деформации с учетом обжатия на участке х 1 е [ 0, а] 4 ] при толщине слоя, равной 5 ₀ = 10 ^{- 2} h . График 1 определяет деформацию ё 1 W , график 2 - деформацию ё₁₂, график 3 - сла-

U + c гаемое деформации £1c = —, график 4 - слагаемое е22c 12     50                                          12

деформации £ ² 2 ^c = A7Yl . Значения деформаций отнесе-¹²    2 dx ₁

ны к значению деформации ё ^ на торце слоя.

2 v^

⁰ Dh

Рассмотрим консоль со следующими геометрическими и механическими характеристиками: a = 0,1 м, h = 0,05 м, v = 0,3, E = 2 -10 ¹¹ Па. На рис. 3 показано поведение функции Y/Y 0 в зависимости от десятичного логарифма отношения 5 ₀ / h для единичной внешней нагрузки.

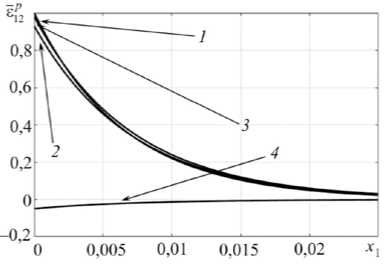
Рис. 4. Зависимость деформаций в слое: 1 - ё W 2 ;

^{2 - е} 12 ^{; 3 - е} 11 2 ^{; 4 - e} 12 ^c

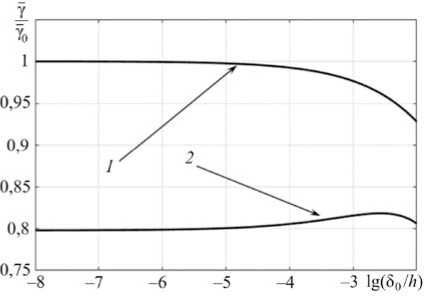
Рис. 3. Зависимость величины ЭП, отнесенной к значению (84), от отношения 5 ₀ / h : 1 - ЭП рассчитано по формуле (83);

2 – ЭП рассчитано на основе формул (72) и (73)

Fig. 4. Dependence of strains in the layer: 1 - е 1 2 ;

c              1c              2c е12 ;       °12 ; е12

Fig. 3. Dependence of the EP magnitude, referred to the value (84), on the ratio 5 ₀ /h : 1 - EP calculated by the formula (83);

2 – EP calculated on the basis of formulas (72) and (73)

На рис. 3 график 1 определяет соотношение (83), а график 2 построен на основе решений (72), (73). Из полученных зависимостей видно, что имеет место сходимость ЭП. При отношении 5 ₀ / h < 10 ^{- 6} значения ЭП практически не меняются. Однако учет обжатия консоли дает снижение значения ЭП на 20 %.

Объяснение данному факту можно дать, рассмотрев

.                           _c u+c . h dФ, зависимости деформации в слое ё 2 =--+--

¹²     5 ₀    2 dx 1

Из рис. 4 видно, что деформации s² ₂ ^c имеют противоположный знак и составляют порядка 5 % от деформации ё ^ на торце слоя. В итоге деформация в слое ё ^ с учетом обжатия консоли составляет около 93 % от деформации ё ^ .

При толщине слоя 5 ₀ = 10 ^{- 6} h характер решения меняется. Деформация ё²/ составляет порядка 0,03 % от деформации ё ^ , и ее можно не принимать во внимание. Однако в этом случае деформация ё^ будет равна 89 % от деформации ё ^ , что приводит к результату, показанному на рис. 3 для ЭП.

Заключение

Рассмотрено НДС ДКБ-образца, близкое к сдвиговому, в рамках модели слоя взаимодействия. Гипотеза об однородном распределении главных деформаций по толщине консолей позволила получить аналитическое решение задачи. Установлено, что ЭП при стремлении толщины слоя к нулю на некотором отрезке, начиная с порогового значения, практически не зависит от тол-

щины слоя. Определено, что учет обжатия консолей на 20 % уменьшает пороговое значение ЭП. Если в результате эксперимента определить критическое значение внешней нагрузки при заданной толщине консоли, то можно найти критическое пороговое значение ЭП. Универсальность данного значения можно установить, сравнивая величины критических нагрузок, определенных теоретически из условия постоянства ЭП при различных толщинах консолей с результатами экспериментов.