Энергетика вихря

Введеиие Вихревой эффект энергетического разделения газов, открытый Ж. Ранком в 1931 году, а затем довольно подробно исследованный Р. Хилшем в 1946 году, на протяжении почти 90 лет остается в центре пристального внимания ученных. Необходимо отметить, что еще до открытия Ранка в работах Максвелла, Шмитда, К. Страховича приводятся теоретические предпосылки энергоразделения газа в закрученном потоке. В результате работ российских ученых были получены оптимальные конструкции основных типов вихревых труб. [1,2,3,4,5,6,7,8] К ним относятся: делящая, охлаждаемая, самовакуумирующаяся, двухконтурная вихревые трубы. Делящая ВТ, в который сжатый газ разделяется на два потока: холодный и горячий. Охлаждаемая ВТ, охлаждающая поток газа через стенки внешним теплоносителем до температуры более низкой, чем температура внешнего теплоносителя. Самовакуумирующаяся ВТ позволяет в раскруточном диффузоре преобразовать кинетическую энергию вихря в энергию давления и тем самым резко снизить давление на оси камеры энергоразделения и существенно повысить эффект охлаждения в ней. Двухконтурная ВТ с дополнительным потоком эффективно работает при р>1, обеспечивая высокую интенсивность теплообмена между основным и дополнительным потоком.

Гипотеза взаимодействия вихрей

Хотя делящая вихревая труба (ВТ) имеет крайне простую конструкцию, процессы, происходящие в ней, настолько сложны и парадоксальны, что только к настоящему времени признаю, что разработанная профессором А. П. Меркуловым гипотеза взаимодействия вихрей, наиболее полно отражает физическую сущность процессов, происходящих в камере энергоразделения. [1,2,5]

Суть этой гипотезы сводится к следующему: после истечения из тангенциальных сопел поток газа образует свободный вихрь, который распространяется до определенного радиуса и смещается вдоль оси трубы к дросселю. Свободный вихрь является устойчивым к силам внутреннего трения и не разрушается ими. Вихрь может начать разрушаться только на своих радиальных границах за чет трения о стенку и взаимодействия с приосевыми элементами. Интенсивность его закрутки при этом падает из-за снижения окружных скоростей при движении вихря вдоль трубы к дросселю, уменьшается радиальный градиент статического давления в вихревом потоке и вихрь все ближе распространяется к оси. [5,6,7]

Уменьшение радиального градиента, в свою очередь, вызывает осевой градиент статического давления, который вынуждает попавший в приосевую область газ изменить свое первоначальное направление осевого движения на противоположное, и двигаться к сопловому сечению. В процессе перехода в приосевую область элементы газа интенсивно турбулизируются. Высокая турбулентная вязкость вынуждает приосевой поток вращаться по закону твердого тела. Обратный приосевой поток по мере продвижения к сопловому сечению закручивается все более интенсивным свободным вихрем.

Кроме передачи кинетической энергии вращения от свободного к вынужденному вихрю между ними происходит интенсивный турбулентный теплообмен при высоком градиенте статического давления, нормального к средней скорости движения потока.

Радиальное перемещение турбулентного элемента газа происходит за счёт радиальной турбулентной пульсационной скорости. Попадая при этом в зону более высокого или низкого давления, элемент будет адиабатно сжиматься или расширяться.

Если после перемещения температура элемента газа окажется отличной от температуры окружающих его элементов, то произойдёт нагревание или охлаждение их, т.е. турбулентные элементы совершают холодильные циклы, отдавая тепло периферийным слоям, источником механической энергии является турбулентность

Турбулентный перенос тепла прекратится (q=0) при достижении изоэнтропного dT k -1 T dp распределения температуры по радиусу —=-----—.

dr k p dr

Эта гипотеза позволяет оценить предельные возможности вихревого эффекта в предположении, что в сопловом сечении полностью завершился энергообмен между вихрями.

Расчетные характеристики вихрей

Используя законы распределения скоростей по радиусу для свободного и вынужденного вихрей, условия механического равновесия газа, изоэнтропного распределения статической температуры по радиусу вынужденного вихря, механической и тепловой сопряжённости вихрей, можно получить выражения для распределения параметров по радиусу соплового сечения, а при заданной геометрии - определить среднеинтегральную температуру холодного и горячего потоков вихревой трубы, как функцию от основных параметров ВТ. Для относительной температуры холодного и горячего потоков ВТ эти зависимости таковы: [3,4,8]

9 x = б ( п , ц ,F_c, d д ) ; 9 г = 6 '( п , ц , F_c, d_ц ) .

Они дают качественное соответствие с экспериментальными характеристиками ВТ, а также описывают явление реверса ВТ (θ x >1 при μ→0) и указывают на возможность получения охлаждения при μ=1 в охлаждаемых ВТ или при μ>1 в двухконтурных ВТ или при

μ=0 в самовакуумирующихся ВТ. При этом расчетные и экспериментальные значения температур значительно отличаются (рисунок 1).

Для уточнения расчетных характеристик ВТ необходимо учесть потери полного давления газа при его истечении через сопловой ввод (газодинамический расчёт), а также регенерацию тепла при противоточном движении охлаждённого приосевого и подогретого периферийного потоков газа в камере энергетического разделения (термодинамический анализ). В основу газодинамического расчёта ВТ положено предположение гипотезы взаимодействия вихрей о существовании двух вихрей: свободного с потенциальным

V течением VT • r = const и вынужденного ® = - = const.

r

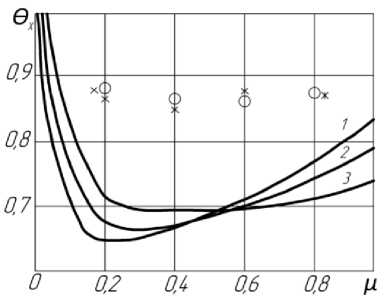
Рисунок 1 – Предельные расчетные характеристики ВТ

Экспериментальные данные

K=1,4; π=5; F_c =0,1; х – Меркулова; * - Гуляева;

О – Мартынова; 1- r _д =0,4; 2- r _д =0,45; 3∙ r _д =0,5.

Можно проинтегрировать уравнение количества движения для невязкого газа dP = p-V-dr r и получить законы изменения параметров газа р, Т, ρ по радиусу.

Граничное условие при решении этого уравнения относительно р определяется из решения уравнения расхода для сечения диафрагмы, которое лежит в сопловом сечении ВТ.

rд pG1 = j p- Vz - 6,28 - r - dr.

Здесь μ - доля охлаждённого потока газа, r _д - радиус отверстия диафрагмы,

V z - осевая скорость в отверстии диафрагмы,

G 1 - массовый расход газа через ВТ.

Осевая скорость, в свою очередь, определится из выражения '                  k -i "

( P ^ ^k p x 1 1 I ,

I p )

V z =±

2^

RT

p

V P i

k -1

k

/

где p 1 - давление на периферии камеры энергоразделения.

Направление движения газа и знак выражения V z определится в зависимости от соотношения величин давления газа p и давления среды p x , в которую вытекает охлаждённый газ.

Значение p 1 получается при условии адиабатичности распределения статических параметров газа по радиусу в виде следующего выражения:

P 1 =

6 , 28 •

—

о V P 1

ц 6 1 RT 1

'          r r I P I ^k„

V z rdr + [ — I V_zrdr r. V ^p 1 )

.

Здесь r a - радиус, на котором осевая составляющая скорости V z меняет свой знак. Граничное условие в уравнении относительно температуры газа на радиусе камеры энергоразделения T=T 1 - находится из уравнения энергии для потока газа в свободном вихре вблизи стенки камеры:

T =

T

1 + — ( M 1 ² — M 2 )

.

Тангенциальная скорость M 1 на периферии камеры энергоразделения выражается через отношение давлений

M 1 =

* p_k

k — 1 V P

k

— 1

— M z .

Относительная осевая скорость M z находится из уравнения сохранения расхода через область свободного вихря в предположении постоянства осевой скорости по радиусу

M z =

G 1

r ₁

.

^1 kRT1 • 6.28 • j prdr r2

Полное давление газа на стенки камеры знергоразделения p k ^* находится с учётом потерь давления в тангенциальном сопле

*          *

Pk = P 1

( ^a c

k — 1

I k

,

V Ф е )

где коэффициент скорости φ c находится по коэффициенту расхода α c из выражения

1 — ~ A²

“ c k + 1 °

k — 1

^{Ф е  1 —} k + T ^Ф е ^А е

.

В последнее выражение входит относительная скорость газа в выходном сечении тангенциального соплового ввода. Она связана с тангенциальной составляющей скорости газа на периферии камеры знергоразделения. Вид зависимости λс от M1 получается из уравнения сохранения момента количества движения a = .    M1  —

7    /k-1

x • 7 -1 ( M 2 + M 2 )

•

rc

.

Расход газа G 1 определяется с учётом коэффициента расхода α c по относительной скорости λ с :

k + 1 2 ( k — 1 )

p,p jk I I      q ( A )

^G1 = « c

^{p 1} c V k + 1 )      ^{4 c}

.

RT где газодинамическая функция расхода по средней скорости в сопле

h q (Ac )bdh q (A) =      ----

Fc

Последней неопределённой величиной, необходимой для замыкания системы уравнений, является радиус разделения вихрей r2, который предлагается определять из вариационного принципа максимума энтропии потока:

*

GR - In — 1- = max . 1                *

pk

В системе присутствует эмпирическая величина - коэффициент расхода тангенциального соплового ввода, для определения которого получена следующая экспериментальная зависимость

¹ . 63             4

^a c = ¹ - Re 0 . 25 ^{( 1 . 03} - ^A ) ‘

Представленная система уравнений решается методом итераций и позволяет определить расход газа через ВТ, распределение параметров газа по радиусу в сопловом сечении и осреднённую полную температуру газа в сечении диафрагмы (так называемая предельная теоретическая температура).

Расчётная температура охлаждённого газа определяется по выражению

T =

XT

f Д p V, T + rdr J o -    ^     2 C p J

/ 0 ^ГД P V z rdr

Для определения давления подогретого газа предложена полуэмпирическая формула Pr = 2 [(Poe + P2 ) + P (P1 - Ptcc )] , предполагающая линейный характер зависимости доли холодного потока газа от давления подогретого газового потока и связывающая величину давления на характерных радиусах (r=0, r=r2, r=r1) соплового сечения.

Термодинамический анализ работы ВТ заключается в определении температуры охлаждённого и подогретого газа путём отыскания и учёта условий, приводящих к адиабатному распределению статических параметров газа по радиусу соплового сечения. Учитывая эти условия, можно найти связь температуры T XT с температурой охлаждённого газа T X в идеализированном процессе, приближённо описывающим процесс передачи тепла в ВТ.

Идеализация процесса передачи тепла в ВТ заключается в предположении, что этот процесс происходит по регенеративной схеме и осуществляется следующим образом.

Газ, вошедший в ВТ, движется по периферии камеры энергоразделения к дросселю ВТ и получает от приосевых слоёв газа некоторое количество тепла q, нагреваясь до температуры T Г . У дросселя газ делится на две части: одна его доля (1-μ) выходит через дроссель в виде подогретого потока с температурой T Г , а другая его доля μ, двигаясь к диафрагме, отдаёт тепло q по пути периферийным слоям газа, охлаждаясь до температуры T X . При этом давление приосевых слоёв газа понижается от p Г вблизи дросселя до p X за диафрагмой. Это первый термодинамический процесс в ВТ. Не рассматривая механизм переноса тепла, можно рассчитать температуры T Г и T X , используя метод термодинамического анализа.

Считаем, что адиабатное распределение параметров в сопловом сечении достигается при отводе от периферийных слоёв такого количества тепла, которое подводится к ним в действительном процессе в ВТ от приосевых слоёв.

Рассматриваем другой термодинамический процесс. Газ с расходом G 1 , двигаясь к дросселю, приобретает от приосевых слоёв тепло q и нагревается до температуры подогретого газа T Г в реальном процессе энергоразделения. От этого газового потока изобарически отводится наружу количество тепла q, при этом температура потока снижается от T Г до некоторой температуры T z . Часть газа с расходом μG 1 формирует приосевую зону и, двигаясь противоточно периферийному потоку, отдаёт ему тепло q за счёт вихревого эффекта.

Температура этой части газа снижается от величины T z до теоретической температуры T XT . При этом давление газа снижается от давления подогретого газа p Г до давления охлаждённого p X . Это второй рассматриваемый термодинамический процесс.

Тепло, отведённое в единицу времени наружу от периферийного потока, с учётом изобаричности процесса определится q = -Gi Cp (T - Tz).

С другой стороны тепло, переданное от приосевых слоёв газа периферийному, равно

SXT q' = Gx J TdS

Sz или приближённо описывается выражением pГ px

' T xt.

I T z

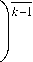
T +T q' = GT---XT— R-In x2

Температуру T z можно найти методом итераций из баланса энтальпий для второго термодинамического процесса:

GCT - G_rCT - GCT + q ' = 0 . p       pz x px

Из равенства q и q ' определяется температура горячего потока Т Г во втором термодинамическом процессе, которая равна температуре горячего потока газа в первом термодинамическом процессе

P r f T xt ) k ^{- 1} P x l T z J

к —А , ^Тг = T + ^ ( T + ^Тхт ) ln Г z 2 k      z XT

Температура охлаждённого газа T X первого термодинамического процесса определится из уравнения баланса его энтальпий.

GCT - G_rCT - G_XCT = 0 . p       pz x px

Предложенный метод расчёта позволяет достичь хорошего совпадения величины температуры охлажденного газа с опытными значениями (рисунок 2).

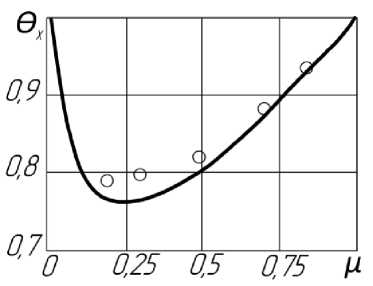
Рисунок 2 – Уточненная температурная характеристика ДВТ:

- расчет; о – эксперимент при π=5

Приведённый выше термодинамический анализ можно применить и к более сложным случаям реализации вихревого эффекта, например, охлаждаемая ВТ, самовакуумирующаяся ВТ и двухконтурная ВТ.

Метод расчета охлаждаемой вихревой трубы

Можно предположить, что течение в идеализированных процессах без отвода и с изобарным отводом тепла имеет одинаковый характер, т.е. температура подогретых периферийных слоёв в процессе с изобарным отводом тепла (p Г =const, T ГД =idem). Уравнение баланса потоков энтальпий при сокращении на G 1 C p будет

T ^- Ц ^Тхд ^- ( 1 ^- Ц^ гд = 0 .

И отсюда по T ГД определяется температура охлаждённого газа T ХД .

Пользуясь этим методом, можно определить температуру охлаждённого и подогретого потоков газа в ВТ с учётом внешнего теплообмена через стенки камеры энергоразделения с окружающей средой. Если принять, что температура стенки камеры ВТ равна температуре подогретых периферийных слоёв газа T ГД (это справедливо в том случае, когда коэффициент теплоотдачи периферийных слоёв газа и теплопроводность стенки значительно превышает коэффициент теплоотдачи от стенки ВТ к окружающей среде), то тепловой поток, отводимый через стенку площадью F K , будет равен

Ч охл = ^а окр F K ^{( T}ГД - ^Токр )

Тогда уравнения запишутся с учётом внешнего теплообмена:

• - для процесса с изобарным отводом тепла

T - T - ( 1 - цТ - ( ТД - Т_г ) - q ₍ = 0 ,

G ₁ C_p

• ■          k -1         "

( n_A k T

T 1 - ц Т хт - ( 1 - ^ ) T z -^ ^TXT- T z In p^- I . T X^ - q °X^- = 0 .

2     \Px J T GCp хz  p

• -    для процесса без изобарного отвода тепла

  T 1   ^{ц Т}хд

  
  

  - ( 1 - ц)1_гд - ^°х^- = 0 .

ГД G ₁ C_p

Температура T Z определяется по уравнению

T_z = T 1 - ( 1 - ц Т д - ^ ^TXT 2-T ^z In

I

I P x J

^*

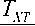
T z

^qоxл =

G 1 C p

Это уравнение решается методом итераций, т.к. в правой его части два неизвестных:

T Z и T ГД , причём они уточняются с каждой итерацией уравнения.

Т д = Т - м - T ) -

« окр • Fk Т^дд - Т окр )

G 1 C p

Уравнение также решается методом итераций. Температура охлаждённого потока газа находится подстановкой T ГД :

ТХД ТГД

^^^^^^в

^v

Т + Т’хт z ХТ

или а • F

Т хд = Т 1 - ( 1 - F )( T_Z - Т^хт ) - ^ кр т^[ Т 1 - Т_О кр + F ( T_Z - Т^хт ) ]■

G ₁ C_p

Анализ решения показывает, что для теплоизолированной ВТ (q охл =0)

• -    при μ=0 T Z =T ГД =T ХД =T 1 *;

• -    при μ=1 T ХД =T 1 , что согласуется с действительными значениями.

Полученные из расчёта значения температуры охлаждённого газа T ХД хорошо согласуются с экспериментальными данными различных авторов (рис. 2). Максимальная погрешность расчёта составляет 4%.

Следовательно, используя метод определения величины температуры выходящих потоков из охлаждаемой ВТ по действительной температуре, полученной при условии адиабатного распределения параметров газа в сопловом сечении, можно найти теоретические характеристики ОВТ.

Учёт влияния пограничного слоя диафрагмы на эффективность работы вихревой трубы

Значительное снижение температурного эффекта энергетического разделения газового потока в ВТ связано с подмешиванием к холодному потоку тёплого пограничного слоя, текущего по плоскости диафрагмы. Этот слой в значительной степени определяет влияние масштабного фактора на повышение относительной температуры холодного потока ВТ. Для уточнения расчётной температуры вихревых труб различных конструкций необходимо определить влияние турбулентного пограничного слоя газа, текущего по торцевой поверхности ВТ к отверстию в диафрагме.

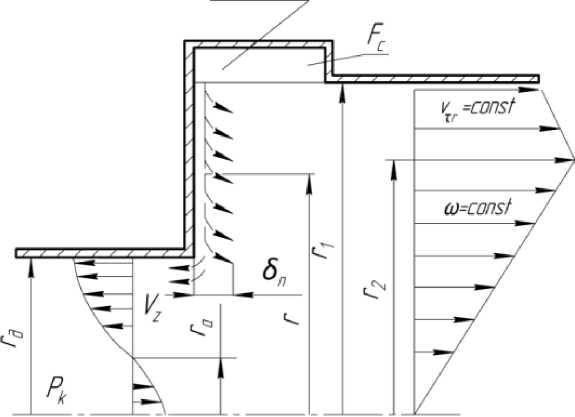
Рисунок 3 – Схема течения пограничного слоя на стенке диафрагмы

Высокий радиальный градиент статического давления в круговом потоке соплового сечения (порядка 105 Па на миллиметр длины радиуса) создаёт значительный радиальный расход пограничного слоя по плоскости диафрагмы, соизмеримый с расходом холодного потока, особенно при больших степенях расширения и малых значениях массовой доли холодного потока.

Пограничный слой формируется (рис. 3) на периферийном радиусе r 1 из элементов внешнего свободного вихря, имеющих полную температуру T 1 *, подаваемого в вихревую трубу сжатого газа, кроме того, пограничный слой толщиной δ п движется вдоль тёплой стенки диафрагмы. Теплообмен пограничного слоя с охлаждённым вынужденным вихрем практически исключён, так как при радиально-круговом движении пограничного слоя имеет место непрерывный расход его в вынужденный вихрь. Этот расход создаёт динамическую тепловую изоляцию пограничного слоя от вихря соплового сечения. Поэтому с достаточной степенью точности можно утверждать, что температура пограничного слоя на всей плоскости остаётся неизменной и равной T 1 *.

При превышении давления в круговом потоке соплового сечения на радиусе r д отверстия диафрагмы над статическим давлением p X за диафрагмой, в первую очередь через отверстие диафрагмы начинает вытекать тёплый пограничный слой. Подмешивание пограничного слоя к вытекающему холодному потоку может заметно влиять на температуру последнего, снижая эффект его охлаждения.

Для проведения расчёта используем решение, полученное в работе [9] для осесимметричного пограничного слоя на неподвижной плоской стенке бесконечного радиуса при вращении над ней газа с постоянной по радиусу угловой скоростью ω.

Условие постоянства угловой скорости ω=const во внешнем от пограничного слоя потоке вполне допустимо на том основании, что при практически используемых умеренных степенях расширения 1,5≤π≤8 свободный вихрь в сопловом сечении распространяется на незначительном периферийном отрезке радиуса от (r 1 до r 2 ), а вынужденный приосевой вихрь занимает основную радиальную протяжённость (от r 1 до оси). Периферийный свободный вихрь, в котором формируется пограничный слой диафрагмы, определяет только граничные условия на r 2 , отражается в значениях интегральных величин, а не в закономерности течения пограничного слоя в области вынужденного вихря от r 2 до r д .

Для получения решения проведено исследование профиля скорости пограничного слоя диафрагмы, оказавшимся близким к закону 1/7, и получено выражение для объёмного расхода пограничного слоя на радиусе r д отверстия диафрагмы в таком виде

V = 3,14 • B • гД V to-v, где ν - кинематическая вязкость, В - постоянный коэффициент, определяемый профилем скорости по толщине пограничного слоя и граничным условиям на r2 . Экспериментально установлено [10] значение В=2,5 в диапазоне 1,1≤π≤8. Отсюда можно найти и массовый расход пограничного слоя

G n = ^Vn ^p n ■

Используя уравнение состояния для пограничного слоя и выражения для статических давлений p д на радиусе отверстия диафрагмы и p 1 на радиусе r 1 соплового сечения, получаем:

P Д = Р 1

ч Рос ,

( k - 1 ) M I 2

⁺   2 r 4   ^{Г д}

k k—1

Расход пограничного слоя диафрагмы определяется

7 , 85 • Г 2 • P * RT

2 ( Pi V + ( k - 1 ) M i² r ₂ k + 1 1 Poc ^J        2 r ?   ^Гд

k k—1

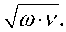
Общий расход G 1 через входное сопло ВТ определяется выражением, относительный массовый расход μ п пограничного слоя может быть определён

G П

P n =

G ₁

Вполне очевидно, что при заданных газодинамических параметрах на входе и выходе вихревой трубы угловая скорость зависит от ее абсолютных размеров и может быть выражена через окружную скорость V τ1 на периферии трубы в виде

V t to = T=2-

r ₂ r ₁

Используя выражения

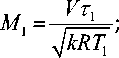
T 1 =

T

k — 1

1 +--- M 2

выражение для μ п преобразуется к виду:

⁵ • ^гд

P n =-----

( Pl ) k*‘ , (k — 1) M12 T ■ ч Poc J         2r24     6

( ^{k +} 1 ) ^ FC • r 2

k k—1

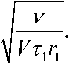
Анализируя последнее выражение, можно выявить ряд особенностей, объясняющих влияние пограничного слоя на характеристики вихревой трубы.

Основной наиболее интересной особенностью является то, что относительный массовый расход пограничного слоя является функцией абсолютного размера (r 1 ) вихревой трубы. Этим, в основном, объясняется влияние масштаба вихревой трубы на ее характеристики – с уменьшением r 1 увеличивается μ п , т.е. степень влияния теплого пограничного слоя на холодный поток.

Второй особенностью является зависимость μ п от относительной площади F_c входных сопел. С ростом последней уменьшается μ п .

Увеличение относительного отверстия диафрагмы r _Д приводит к возрастанию μ п .

При увеличении в вихревой трубе степени расширения π величина μ п несколько увеличивается, так как при этом уменьшается относительный радиус r ₂ разделения вихрей.

Найдем зависимость температуры холодного потока от величины μ п в случае

подмешивания пограничного слоя к холодному потоку.

Полная температура холодного потока T хп * с учётом подмешивания пограничного слоя определяется из уравнения теплового баланса

^{( P + p} n ) T xn = ^{p T}x ^{+ P} n^T1 ■

Отсюда можно выразить относительную температуру θ хп холодного потока в случае подмешивания к нему пограничного слоя

„*       .      вх + ^L

^ТХП _ ^Цв Х + М и  ____ Ц ^в ХП = ^* =          =         ■

T     Ц + Ц и    1 + ^ц и

Ц

На рис. 4 представлены расчётные зависимости влияния пограничного слоя на относительную температуру холодного потока как функции ц и r i при п=5 и Fc = 0 , 1 для а) 7_Д = 0 , 4 ; б) 7_Д = 0 , 5 ; в) ГД = 0 , 6 . Анализ зависимостей показывает, что с уменьшением ц степень влияния пограничного слоя на θ х возрастает, особенно в области μ<0,2, достигая 20…40%. При μ>0,5 степень влияния снижается до 2…3%. Степень влияния заметно возрастает с уменьшением абсолютных размеров (r 1 ) вихревой трубы, особенно в области r 1 <0,01 м, имея приблизительно обратную квадратичную зависимость от радиуса вихревой трубы.

С ростом относительного диаметра r _Д отверстия диафрагмы степень влияния возрастает при всех μ для всех значений абсолютных размеров вихревой трубы.

Сравнение характеристик ДВТ показывает влияние F_c для значений 0,1 и 0,08 на относительную температуру ВТ. Увеличение F_c в рассматриваемых пределах практически не приводит к снижению значений θ хп , но смещает характеристики в сторону меньших значений μ.

Если учесть, что холодопроизводительность вихревой трубы, а, следовательно, и ее адиабатный КПД, являются функцией произведения (1-θ хп )∙μ, то можно сказать, что всегда при проектировании вихревой трубы целесообразно выбирать меньшие значения относительной площади сопла F_c . Характер изменения зависимостей θ хп от различных параметров позволяет разработать обоснованную систему коэффициентов для расчета вихревых труб. Следует так же отметить, что подсос пограничного слоя повышает значения θ хп ⁄θ х на 10…15%. Влияние подсоса пограничного слоя с ростом степени расширения возрастает.

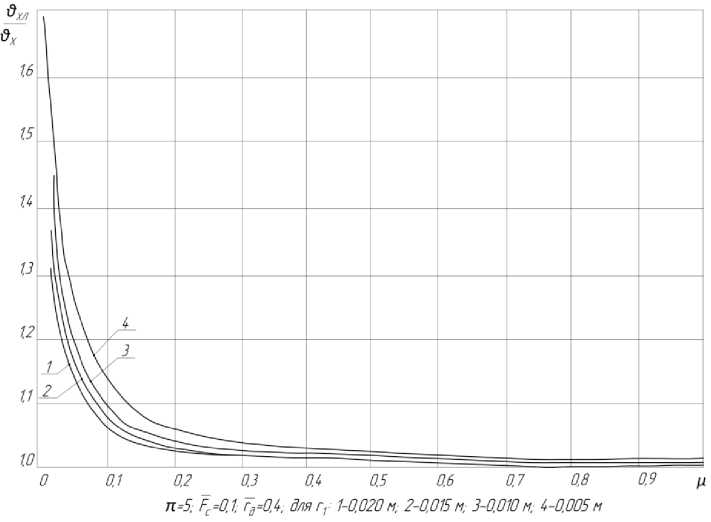
Рисунок 4 – Зависимость коэффициента влияния пограничного слоя ^ХЛ от μ θ Х

Метод расчёта параметров газового потока в самовакуумирующейся вихревой трубе

Самовакуумирующаяся вихревая труба (СВТ) представляет собой цилиндрическую вихревую трубу, закрытую с одного торца плоской стенкой, а с другого конца совмещенную с радиально – щелевым диффузором. К плоской стенке прилегает тангенциальный сопловой ввод. Передняя стенка радиального диффузора сопрягается с трубой по окружности или лемнискате. В приосевой зоне трубы располагается металлический стержень, служащий теплоотводом. Основные геометрические размеры СВТ приведены на рис. 5.

Тангенциальный сопловой ввод газа в СВТ обеспечивает вращательное движение газа в ней, которое за счет центробежных сил создает радиальный градиент давления. В результате на оси трубы образуется область газа с пониженным давлением и температурой. Большая величина скорости газа в трубе и большая степень его турбулентности обеспечивают интенсивный отвод тепла от стержня, помещенного на оси трубы.

Подавая в СВТ газ под давлением (обычно располагаемая степень расширения газа π=1,1…8), можно получить на оси трубы температуру газа более низкую (на 10…120 К), чем температура газа, входящего в СВТ. Используя стержень в приосевой зоне как теплоотвод, можно понижать температуру и снимать нагрузку с объекта охлаждения.

Метод расчета параметров газа в СВТ основан на использовании газодинамической поправки для течения газа в тангенциальном сопле и критериального уравнения для коэффициента теплоотдачи от цилиндрического стержня к вращающемуся газу. С помощью этого метода можно определять температуру и давление на любом радиусе СВТ, расход газа через нее, а так же температуру стержня – теплопровода, помещенного на оси трубы, с подведением тепловой нагрузки и без нее. Основное отличие СВТ от расходных ВТ заключается в отсутствии холодного потока (μ=0). Это накладывает свои особенности на расчет параметров СВТ с использованием Гипотезы взаимодействия вихрей.

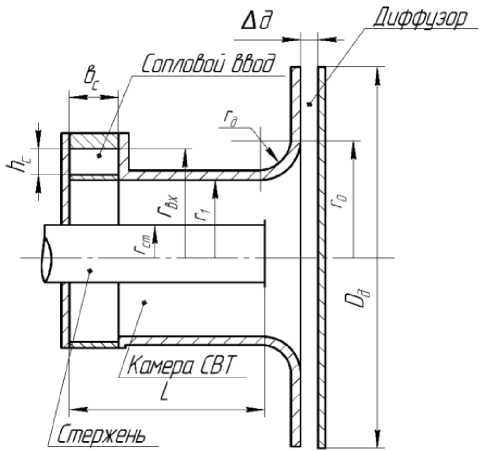
Рисунок 5 – Схема и основные геометрические размеры СВТ

После интегрирования уравнения сохранения количества движения получим следующее распределение давления по радиусу СВТ:

в свободном вихре

88                  Агротехника и энергообеспечение. – 2022. – № 3 (36)

в вынужденном вихре

p = P 1

( k - 1 ) M 12 f 2

2 F2

² V r 2

- 1

k k-1

^{k -1}                    / X

P = P 1

^f P oc A ^k , ^{( k - 1 ) M 2 f} r²

V P 1 J          2 V r J

k k-1

Число M 1 на периферии СВТ можно найти, если известны полное и статическое давления на r 1 . Расход газа через выходное сопло определится из учета G 1 =G. В формуле присутствует величина составляющей скорости M z . Можно принять величину осевой скорости в потенциальной области течения постоянной по радиусу. Тогда расход газа через потенциальную область течения (r 2 ≤r≤r 1 ) запишется как

G =

MzPk ^ • 6,28 • r1 f- r2

1 - k - ¹ M 2

f 1

=2

V ^r2

A

- 1

k -1

r d r

-

k 21 ( m 1 ² + m Z )

k +1

² ( ^k —1 )

Отсюда находится

k +1

F_c f 2 A²⁽ k ^-1) Г    k -1/.,2

M, = ——    1 + — M 2 + M 2

z 2 V k + 1 J L 2 ^{( 1} z )

k +1

2( k-1) pk pk

q (^)

r ₂

1 - k -¹ m 2

f

=2

V r 2

k -1

r d r

Величина полного давления p k * находится с учетом потерь при расширении газа после тангенциального входного сопла:

V ²

Pk = P1 - ZcPc -^,, где ζc – коэффициент потерь на расширение в сопле, ρc, Vc – плотность и скорость газа на выходе из сопла.

Применяя газодинамические функции, последнюю формулу можно переписать в виде:

*

Pk = P 1

1 - ZkF ^>( ^)

Коэффициент потерь ζ c можно подсчитать по эмпирической формуле:

_z = 183 , 6

^{Z c} Re⁰⁵³³

1 - n

F c

( 1 - r^¹ ) J '

Однако, для полного газодинамического расчета СВТ необходимо наложить следующие ограничения на значения рассчитываемых величин:

• -    из принципа максимального расхода через тангенциальный сопловой ввод следует ^ с ^^ скр ., при которой q ( Я ) = max ;

• -    из недопущения сверхкритической скорости на стенке камеры СВТ M 1 ≤1.

Параметры газа на оси СВТ определяются как:

k - 1

P oc = P 1 1 — 2   M 1

( 1

=2 — ¹ I r 2

X

У

k — 1

;

*

^ oc = -1- p oc

*

p ₁

k - 1

₁ k 1 _ -2 ^p 1 1 ^— — M 1

=2

I r 2

-

X

1 , k — 1

У_

где π oc =π* - степень расширения воздуха в вихре. Относительная температура по оси СВТ

9 oc

1 — — m 2

oc

T

(

\

I r 2

—

k — 1

1+— m 2

У

.

Если сделать допущение о том, что размещение на оси СВТ круглого стержня не изменяет газовой динамики в ней, то нетрудно найти давление и температуру торможения на любом радиусе стержня:

• -    скорость на стержне радиусом r c 2

V c = m 1 j-rtt r^, r ₂

• -    статическое давление

  k k — 1

  
  

k ^—1                    / ~ X

Pr e = P 1

⁽ p oc ) ^k + ( ^{k —} 1 ) ^M 1 ⁽ r c_ I P 1 У           ²      [ Г 24 У

Относительная температура потока на внешнем радиусе стержня

„   т *  T rc oc °oc =   =   +

T ₁ T ₁

( k — 1 ) M 1 ²

(tX ^c

1 + k-¹ m 2 1 ^r 2 У

Если на стержне выделяется тепловая мощность N, то температура стрежня будет

Tc = Tc+ -NT, a- Fc где коэффициент теплоотдачи α определяется из критериального уравнения

Nu = 0 , 739 • Re °’⁸

Здесь число Рейнольдса Re = ^c^r .

Ц

Изменяя величину r2 , рассчитываются все остальные параметры, находится максимальное значение энтропии потока, которому будет соответствовать истинное значение r2 , полученное из вариационного принципа максимума энтропии потока.

Полное давление на входе в диффузор определяется как n *                   V22

pд>иф рн z диф p2 2 , где ρ2, V2 – параметры газа на радиусе r2.

Коэффициент потерь давления в диффузоре ζ диф определяется по методу эквивалентного диффузора

С диф = 0 , 031 + 0 , 064 ( 5 экв - 12 ) 2 .

Числовые коэффициенты подбирались по экспериментальным данным замера полного давления в радиально-щелевом диффузоре СВТ. Эквивалентный угол раскрытия диффузора определяется как

5 ^ = ² arctg

0 , 392 • M z

( м 2 + m_z² ) . ( 1 + Д диф )

Принимая допущение о равенстве p k * и p диф *, можно получить выражение для статического давления p 1 на стенки камеры СВТ:

Pi = pJ *

1 - —м 2

( 1

-

I r 2

-

\

У

•

1 - k -¹ м 2

I ^Г 2

-

У

k -1

которое замыкает систему уравнений относительно M 1 , p k *, r ₂ , p 1 для расчета СВТ.

На рис. 6 приведены значения качественно совпадающих с опытными данными θ c (π), предложенный метод расчета СВТ позволяет при определенной геометрии СВТ определить температуру стержня (тепловода) на заданных режимах.

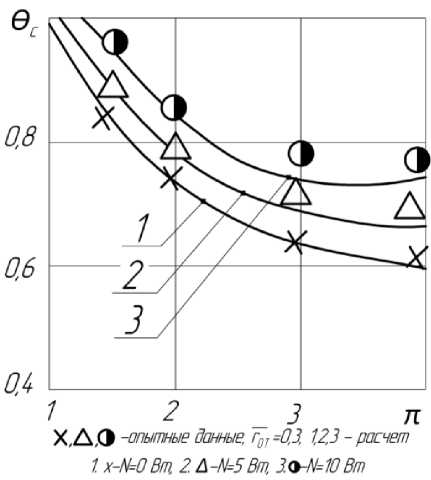
Рисунок 6 – Зависимость θ с от тепловой нагрузки на стержень и степени расширения СВТ

Выводы. В результате исследования работы ВТ разработан метод уточнения расчета характеристик ДВТ и других типов ВТ с использованием газодинамической, термодинамической и тепловой поправок.

Учет эмпирических поправок позволяет провести математическое моделирование процессов ВТ в вихревых системах охлаждения. По предложенному методу разработаны методики и программы расчета действительных характеристик вихревых труб для систем кондиционирования. [4,7,8]

Serebryakov Rudolf Anatolyevich, Candidate of Technical Sciences, Leading Researcher, Federal Scientific Agroengineering Center VIM (FGBNU FNATS VIM), 109428, Russia, Moscow, 1st Institutskiy proezd, 5, tel. 8(917(576-97-83,