Энергоэффективные технологии жизнеобеспечения с солнечными системами теплоснабжения

В России за 15 лет перестройки основной объем производства овощей, мяса, молока переместился из сельхозпредприятий (11,5%) в фермерские и личные подсобные хозяйства — 86%. И эта продукция производится в основном в животноводческих помещениях, временных пленочных теплицах, где не поддерживаются нормируемые параметры микроклимата. Создается проблемная ситуация, заключающаяся в необходимости надежного и устойчивого энергообеспечения сельского хозяйства, фермерских и личных подсобных хозяйств экологически чистыми источниками энергии. Таковыми являются возобновляемые источники энергии (ВИЭ). Из всех видов ВИЭ наибольшее развитие в мире получило преобразование солнечной энергии в тепло невысокого потенциала, используемое для теплоснабжения. Далее речь пойдет о методах создания энергоэффективных технологий на объектах сельского хозяйства для производства экологически чистой продукции с использованием гелиотехнического оборудования [1, 2, 3].

Метод создания энергоэффективных биотехнических систем

В животноводстве в настоящее время большое значение приобрел вопрос снижения энергозатрат на отопление и вентиляцию ферм в связи с резким подорожанием энергоносителей. Расходы на потребляемую энергию в отопительный период года сопоставимы с расходами на кормление животных. Многовариантность технических решений для снижения энергозатрат при формировании нормативного микроклимата в животноводческих помещениях свидетельствует о необходимости комплексного учета взаимовлияния технических средств, биоорганизмов, внутренней и наружной среды, что вместе составляет единую биотехническую систему (БТС).

Для установления свойств и взаимосвязей между факторами и процессами, влияющими на состояние БТС, необходимо применить метод системных исследований . Для обоснования рациональных режимов работы БТС необходимо знать влияние на продуктивность животных суммы параметров воздушной среды помещения: температуры Т , влажности φ, аммиака NH 3 , углекислого газа СО 2 , подвижности воздуха V в виде функции продуктивности:

П = ƒ(Τ вн ,φ вн ,NH 3 ,CO 2 , V ) (1)

Для сложной системы в целом построить математическую модель теоретическим методом не представляется возможным. Поэтому математическая модель БТС получена экспериментально-статистическим методом.

Параметры, характеризующие протекание технологического процесса в БТС, классифицируем на входные и выходные.

Входные параметры : мощность вентиляционно-отопительных установок (ВОУ) — Р, кВт; подача вентиляторов — L, м³/ч ; корма — К, кормовая единица; тепло — Q ж , кДж/ч и влаго-выделения животных — D ж , г/ч ; количество теряемого тепла: на испарение — Q исп , кДж/ч ; через ограждающие конструкции — Q огр , кДж/ч ; параметры наружной среды: температура — θ н °С , влагосодержание — d и , г/кг .

Входные параметры делим в свою очередь на регулируемые К, Р, I и нерегулируемые Q ж , D ж , Q исп , Q ог , θ н , d н , которые взаимосвязаны между собой (кроме кормов) уравнениями теплового и влажностного баланса.

Выходные параметры — это группа параметров, зависящая от входных параметров и подразделяемая на показатели процесса (продуктивность — П, кг, минимум приведенных затрат — е, руб/кг), а также на показатели, проверяемые на технологические ограничения (по температуре — θвн, °С; относительной влажности — φвн, %; содержанию аммиака — NН3, www.rypravlenie. ru

том 7 № 1 (10), 2011, ст. 2

мг/л, углекислого газа — СО2, % и подвижности воздуха — v,м/с) воздушной среды коровника, которые налагаются условиями нормального технологического процесса и возможностями ВОУ. Параметрическая схема входных и выходных параметров БТС приведена на рисунке 1.

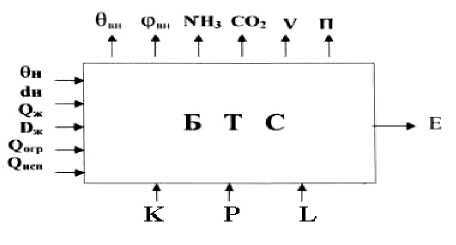
Рис. 1. Параметрическая схема входных и выходных параметров БТС

Полученная ранее автором модель действия параметров микроклимата внутренней среды помещения на продуктивность коров П=ƒ (φ вн , θ вн , NH 3 , CO 2 , v) :

Π( θ , ϕ )=5,043+1,315 θ - 7,653 ϕ - 0,389( θ )2 + 3,029( ϕ )2 - 0,38 θ ⋅ ϕ ;(2)

θm ϕm               θm ϕm θm          ϕm θm позволяет получить модель эффективности функционирования БТС жизнеобеспечения молочных коров, используя выражение:

е = (0,15К+Э)/П, где: 0,15 — нормативный коэффициент; К – капиталовложения во все объекты фермы

(трансформаторные подстанции, ЛЭП технологическое оборудование), руб./сутки;

Э – эксплуатационные, затраты на производство продукции руб./сутки.

Эксплуатационные, затраты на производство продукции (Э) представляет собой сумму:

Э = З + И + З q + а

пом к пом

+ а пом +а от к от,

где: З — зарплата обслуживающего персонала, р/сут.; И — стоимость кормов, воды, электроэнергии без отопления, р/сут.; Зq — затраты на теплоту, подаваемое отопительновентиляционной системой, р/сут.; aпом и кпом — нормы отчислений на амортизацию и текущий ремонт зданий, систем теплоснабжения, отн.ед. П = ƒ (θвн, φвн,) — суточная продуктивность коров, кг.

Величины к, З, И, aпом, кпом, aот, кот  будут оставаться постоянными для одного расчетного варианта, обозначим их через А, тогда (3) примет вид:

е = (А + Зq)/П ;                                                                      (5)

или www.rypravlenie. ru

том 7 № 1 (10), 2011, ст. 2

e

А + α {[к F + с (D m + D F)/(d - d )]( θ - θ )-m·Q + 2.4D F} 0           ж;         и и вн н вн н           ж          и и

;

Модель была принята в качестве критерия оптимизации процесса, как минимальная величина стоимости затрат на получение I кг молока в сутки при П_тах . Оптимальным будет такой режим работы БТС, при котором для любой комбинации входных нерегулируемых параметров О н , 4_н будет найдено такое значение регулируемого параметра расхода теплоты, при котором е приняло бы минимальное значение при соблюдении ограничений:

П=П тах ; О = О опт ; ф=ф опт ; NH₃<0,02 мг/л; СО 2 <0,25%; и < 0,3 м/с. (7)

Для ведения технологического процесса по оптимальной экономической траектории e(t) необходимо, чтобы в каждый момент времени текущему значению — температуре 14°С — соответствовало значение влажности 70%, при которых обеспечивается минимальное значение мгновенных затрат.

Зависимость e = f (О,Р,ф) будет изображаться поверхностью отклика в четырехмерном пространстве (две оси ОР, Оθ ) и осью Оφ, которую зрительно представить невозможно. Однако характер влияния третьей переменной φ можно представить как изменение функции e = f(О,ф) в зависимости от уровня фактора ф, координаты которого находятся в третьем измерении. Графически это мы представим в виде набора 3-х поверхностей e = f(O,P) при трех уровнях ф (70, 80, 90%), каждая поверхность является трехмерным сечением некоторой четырехмерной, описываемой e =f (О,P,ф) (рис. 2).

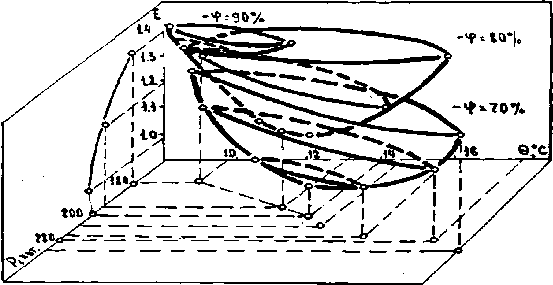
Рис. 2. Зависимость затрат от температуры, влажности воздушной среды помещения и мощности ЭВОУ при θ н = -18 — -23°С.

Откуда видим, что минимуму приведенных затрат также соответствует оптимальная температура 14°С и влажность 70%. Выбор любого значения мощности ВОУ, отличного от мощности установки, соответствующего оптимальным значениям О и ф, вызывает увеличение затрат по сравнению с минимальными.

Моделирование энергоэффективной солнечной теплицы

В обычных теплицах из-за большой площади светопрозрачных поверхностей возникают значительные теплопотери, для компенсации которых требуется большой расход топлива. Теплица должна воспринимать в отопительный период максимальное количество солнечной радиации, которое можно регулировать выбором оптимального значения угла наклона α прозрачной поверхности к горизонту (рис. 3). Связь между α и высотой солнца h о запишется как: α = 90^o - h o или с учетом широты местности φ и угла склонения солнца δ: h о =90^о–φ–δ .

Для условий г. Улан-Удэ — широта φ=52º3', теплица площадью 100 м², при числе дней работы в году — 180, с 15 февраля по 15 ноября, при α = 60º, h о = 30º — будет иметь оптимальные геометрические размеры пола 18,2х5,5 м.

Формула зависимости геометрического показателя от размеров элементов ограждающих конструкции и высоты солнца П= f(h о, b,H 0 ,L) имеет вид:

( b + b *co^s( h o ) - H o ) + H L +     b -*^sin²⁽ h o )* h o + b ²*cos⁽ h o ) - H o       h )*( b *^cos( h o ) + H o ))

П =            sin( h o )                               2 ________________ sin( h o )                       2         2      (8)

(b * Sin(ho) + b *cos(ho)+ Ho * cos( ho)) * L sin(ho)

где b — ширина прозрачного ограждения; H о — высота тыльной стороны стены; L — длина теплицы.

Определение теплопроизводительности теплицы с закрытой пассивной солнечной системой

Для эффективной работы солнечных теплиц необходимо избыток тепла аккумулировать для выравнивания дневных и ночных температур. Для чего рассмотрим теплицы с закрытой пассивной солнечной системой (ПСС), которые отличаются простотой, прежде всего, с точки зрения конструктивного решения, и выполняются как функции элементов здания, так и функции восприятия и аккумулирования тепла (рис. 3) [1, 2].

Условные обозначения: b — ширина светопрозрачного покрытия; α — угол наклона;

E 2 D = Н о — высота тыльной стороны стены; h о — высота солнца.

www.rypravlenie. ru

том 7 № 1 (10), 2011, ст. 2

Уравнение для закрытой ПСС имеет вид:

( M * C p ) вн

* вн = а * F *Г t .— т ] + а * F   *Г t  .— т ] + г       а вн      ст   [t вн(т)    т ст(—е,т)] а вн покр Г^вн(т)    т покр(—e,т)]

n пер                пер

^{+ а} вн ¹ лол   ^Г t BH ( т )     t пол ( — e , т ) ^{] + а} вн ^ вн     ^Г t BH ( т )     t ( — e , т ) ^{] + 1} окк о ОК   ^Г t вн ( т )

^— tH ( т ) ^{] +}

+ V вент

* Р н

Ч' 4*17      Д-F *а - О +(т*С} *17  -t™ р Гt вн(т) tn(т)] о ок qпогл(т) Qвн(т) + (m     р ) ТП Г^вн(т) ^вых(т)

где: (т*С_р)_ТП — массовый расход нагретого воздуха поступающего от

теплоприемника; С _р1ТП — удельная теплоемкость воздуха от теплоприемника; t ™ (т) —

температура воздуха на выходе из теплоприемника ; Р_ок — площадь окон; т _вн — масса внутреннего воздуха; С _р,_вн — удельная теплоемкость внутреннего воздуха ; t_вн(т) — температура внутреннего воздуха ; т — время; а_вн — коэффициент теплообмена внутренних поверхностей ограждающих конструкций; 1_ст(-ет) — температура внутренней поверхности наружной стены; F_cm — площадь внутренней поверхности наружных стен ; F_nок — площадь внутренней поверхности покрытия; t_пок(-ет) — температура на внутренней поверхности покрытия; F_nep — площадь внутренней поверхности перекрытия; 1_пер(-ет) — температура внутренней поверхности перекрытия над подвалом; F вn _н — площадь поверхности внутренних

n перегородок, перекрытий; Гн (-е(т)) — температура поверхности перегородок; ^ (т*Ср)об 1

— теплоаккумулирующая способность массы различного внутреннего оборудования ; t_об(т) — температура на поверхности внутреннего оборудования ; К_ок — коэффициент теплопередачи через светопрозрачное покрытие ; t_н(т) — температура наружного воздуха; V — объем поступающего наружного воздуха извне за счет инфильтрации и через вентиляционные каналы наружного воздуха; р_н и С_р — плотность и теплоемкость наружного воздуха ; F_ок — площадь остекления пассивной системы; д _погл (т) — плотность поглощенной внутренним объемом солнечной радиации; Q_вн(т) — внутренние тепловыделения.

Определение теплотехнических параметров солнечной теплицы (рис. 4), в северной стене которой размещен абсорбер-теплоприемник II. Оптимальные значения углов наклона поверхности светопрозрачного покрытия принимаем равным а ₁ =60°, а ₂ =30 Г3].

www.rypravlenie. ru

том 7 № 1 (10), 2011, ст. 2

Рис. 4. Теплица с закрытыми пассивными солнечными системами

Условные обозначения:

• 1    — прозрачная изоляция; 2 — теплоизолированная передняя стенка;

• 3    — теплоизолированная северная стенка; 4 — крыша; 5 — теплоизоляция;

• 6    — теплоизолированный фундамент; 7 — аккумулятор; 8 — вентилятор;

• 9    — циркуляционные каналы.

В качестве материала пола, потолка, стены берем плиты перекрытий — железобетонные, армированные стержнями из стали Ат+V.

Определим температуру внутренней поверхности τ в стен потолка и пола

τв’ = 0.765* tв + 0.235*tн - стен (7); τв’ = 0.785*tв + 0.215*tн — потолка;(10)

τв’ = 0.78*tв + 0.21*tв — пола.(11)

Подставив значения получим:

αвн = 8.7 Вт/м² ºС; Fст = 42.1 м²; Fпот=70.2 м²; Fпол= 100 м²; m*Ср= 204*103 Дж/ ºС в уравнение (6), получим уравнение:

(m*Ср) dtвн = 5,95(tвн - tн) – q .

dτ

При дискретном изменении температуры во времени формула примет вид:

t6H - L = 0,035 *(t„ - L ) + 0.0029* q„.(13)

• BHi +1       BHi                          Hi +1       BHi

Для определения теплопроизводительности пассивного теплоприемника используем формулу :

QТП = (mСр)погр∙(tпогр - tвн)∙(a-1), Вт,(14)

где: tвн — средняя по объему здания внутренняя температура воздуха, оС. а — сторона теплицы, где расположен теплоприемник; (mcρ)погр — масса пограничного слоя воздуха на 1 метр.

Изменение температуры воздуха в пограничном слое, определяем по формулам:

для абсорберов I , II:

1погр(1+1) - 1вн(1) — 0,365 (1н(1+1) - 1вн(1)) + 0,016qпогл(i+1);(15)

для абсорбера I :

• tпогр(i+1) - tвн(i) — 0,3 (У.р+Г) - tвн(i)) + 0,0132 qпОгл(t+i) .

(тс_р)_погр находим по формуле:

тпор 36006-р- Уср —38,9 кДж/м-°С ,(17)

• где: 6 = 1 см — толщина пограничного слоя; р = 1,2 кг/м ³ ;

У ср = 0,9 - 1 м/с; С = 1 кДж/кг/град.

В уравнение теплового баланса для закрытой системы вводим слагаемые ( т * C_p ) абр и ( Тр — 1 вн ); получим уравнения:

для абсорбера I: tвн(i+1) - у® — 0,259*(У(1+1) - 1^+0,015* qaп6oгл(i+1) + 0,019*qп;(18)

для абсорбера I, II: tвн(i+1) - у® — 0,144*(У(1+р - 1вн(1))+0,016* qaп6oгл(i+1) + 0,009*qп.(19)

Для определения количества теплоты, поступающей от теплоприемника, подставим в формулу (14) полученные значения (т*С_р)_погр и *(t_погр - у_н) и получим:

Q П — 38.9-17.2 -Опогр - Ун) — 0,185- (Уогр - Ун) кВт-ч/1 С.(20)

По полученным формулам рассчитаны почасовые значения температуры воздуха внутри теплицы. Результаты расчета солнечной теплицы показали, что она может эффективно функционировать с 15 февраля по 15 ноября [2, 3], причем:

• 1.    Оптимизация размеров конструкции теплицы на 1 месяц сокращает отопительный период ив 1,5 раза повышает теплоаккумулирующую способность теплицы, причем в апреле — в 2,3 раза, а в октябре — в 3 раза, что очень важно для ранневесенних и поздне-осенних теплиц для экономии тепла.

• 2.    Традиционная система отопления может быть отключена в сутки: апреле (14 ч.), мае (16 ч.), сентябре (14 ч.) и октябре (12 ч.).

• ³ ' Теплопроизводительность ПСС составит за отопительный период 185 кВт^ч/м² Метод определения энергетической эффективности аккумуляторов теплоты с теплоаккумулирующими насадками галька и цеолиты

В аккумуляторах емкостного типа, где используется нагреваемый аккумулирующий материал без изменения его агрегатного состояния, происходят последовательно или одновременно процессы нагревания и охлаждения теплоаккумулирующего материала (ТАМ)

www.rypravlenie. ru

том 7 № 1 (10), 2011, ст. 2

либо за счет солнечной энергии, либо через теплообменник. Этот способ аккумулирования тепловой энергии наиболее широко распространен. Представляет интерес использование в качестве ТАМ природных пористых материалов, их определяющими свойствами являются межзерновая пористость, размер и форма зерен, плотность и механическая прочность.

Гидравлический и теплотехнический расчет характеристик аккумуляторовтеплоты с насадками галька и цеолиты

Расчет потерь давления ведем по формуле:

Δ P =ξ ^H ⋅ ^{V 02 ρ в}[ ^{(1 -ε ) 3 - n} ψ ^{3 - n}],

d, 2         ε ³

где : ξ — коэффициент сопротивления насадки; Н — высота насыпи, м; ψ — коэффициент формы зерна; d э — эквивалентный диаметр; V о — скорость воздуха, отнесенная ко всему поперечному сечению насадки, м/с; ε — порозность насадки; ρ в — плотность воздуха, кг/м³ ; n — показатель степени, зависящий от критерия Рейнольдса для турбулентного течения, n=2.

ξ находим из эмпирического выражения: ξ = 10Re^-0,2 при 1000

ξ г = 10/Re^0,2 = 10/3045,2^0,2 = 2 — для гравия ;

ξ ц = 10/2926^0,2 = 2,02 — для цеолитов .

ν=14,16*10^-6 м²/с — коэффициент кинематической вязкости. Значения ξ почти одинаковы для обеих насадок. Значения ΔР согласно (19) равны:

ΔР ц = 71,4 · 0,384 · 5,38 = 147 Па — для цеолитов;

ΔР гал = 71,4 · 0,384 · 3,38 = 90 Па — для гальки.

Расчет потребной мощности вентилятора на валу:

На входе в ТА вентилятор должен обеспечить давление, значения которого определены выше. Его мощность находим из соотношения:

N=GΔP/η·1000, кВт,                                                          (22)

где: η = 0,65…0,85 — КПД вентилятора; G — массовый расход воздуха, м³/с; ΔP — потери давления, Н/м².

G=0.8 м³/с; ΔP г =90 Н/м²; ΔP ц =147 Н/м²; N г =110 Вт -; N ц = 170 Вт.

Количество тепла, аккумулируемое в насадке , находим по уравнению:

Q акк = α н *F н ΣΔТ н ,                                                                   (23)

• где: F н — площадь насадки, обдуваемая тепловым потоком, м². α н — коэффициент теплоотдачи с единицы площади, Вт/м² * К;

  www.rypravlenie. ru

  
  

  том 7 № 1 (10), 2011, ст. 2

0,8( ^{ω d Т})^0,5 λ ^ν α _н =                ;

dТ анг = 10,3 Вт/м2 * К; анц = 12 Вт/м2 * К

ΔТ — приращение температуры насадки найдены из балансовых уравнений энергии воздуха и насадки. Максимальный перепад температур ΔТ в начале зарядки и в конце составил у насадки: цеолиты — ΔТ = 4,5 К; галька — ΔТ = 3,2 К.

Расчет энергоэффективности тепловых аккумуляторов с разнымитеплоаккумулирующими насадками ведем по уравнению:

Qакк =αНΠd4Т H′аVΔTН

• и преобразуем его, подставляя значения входящих в него параметров:

dТ = 0,634    2 ,м(26)

δсраV ау=6^(1-е)/5с,(27)

где: ω=V/ε, Н' = 0,00047*G (для насадки цеолиты);

Н' = 0,00041*G (для насадки галька).

Размерность G задана в [кг/м2*ч]. После подстановки всех значений получим уравнение, учитывающее влияние семи переменных на количество аккумулируемого тепла ТАН:

Q акк = 5,69 ^V [ ψ (1 -ε )]^{0,25 C в 3600 G} Δ Т (28) ε C_Н ρ _Н δ _ср

Полученное уравнение позволяет определить наиболее оптимальный режим аккумуляции тепла в насадках при заданных разных значениях массового расхода воздуха G и скорости V для различных сочетаний параметров слоя (е, 5_ср, у), при фиксированной плотности и удельной теплоемкости насадки.

Уравнение позволяет также рассчитать оптимальную геометрию слоя: высоту Н , поперечное сечение аккумулятора F, что ранее в уравнениях энергетического баланса не учитывалось. После подстановки значений с в , с_н, р_н, которые постоянны для определенного вида насадки, получим:

Q = 10,0 ^V [ ψ (1 - ε )] ^{0,25 G} Δ Т ак цеолиты к                ε                       _δ          ^;

www.rypravlenie. ru

том 7 № 1 (10), 2011, ст. 2

Q = 8,43 V[ψ(1 - ε)]0,25 G ΔТ аккгалька               ε                      δ

Важными факторами, влияющими на эффективность аккумулятора являются энергетические затраты на фильтрацию теплоносителя через слой и получаемый при этом теплосъем с поверхности насадки. В результате проведенных теоретических и экспериментальных исследований нами получена формула энергетической эффективности ТАН:

Е=

4,6 ⋅ 10⁷ ε ^2,5 δ ^0,2 Δ T ср

C Н ρ Н HV^1,3[(1 -ε ) ψ ]^0.75 Δτ ^,

где: £ — порозность; 5_ср — средний диаметр зерна насадки, м; с_н — удельная теплоемкость, кДж/кг*К; р_н — удельная плотность насадки, кг/м³; Н — высота слоя, м; V— скорость воздушного потока, м/с; ψ — коэффициент формы зерна; ΔТ — разность температур насадки в начале и в конце зарядки; Δτ — разность времени между началом и

окончанием аккумулирования.

Полученная формула универсальна, т. к. позволяет сравнивать между собой различные варианты ТА еще на стадии проектирования с различными параметрами насадки (г, у, 5) ; геометрией слоя (H, F); скоростями движения теплоносителя ( V) ; удельной теплоемкостью с н и плотностью насадки ρ н . В нашем случае при известных значениях удельной теплоемкости с_н и плотности р_н гальки и цеолитов формула (31) примет вид:

13,0 ⋅ε ^2,5 δ ср ^0,2 Δ T Е =

HV^1,3[(1 - ε ) ψ ]^0.75 Δτ

для гальки;

15,5 ⋅ε ^2,5 δ ср ^0,2 Δ T Е =

HV^1,3[(1 - ε ) ψ ]^0.75 Δτ

для цеолитов.

Каждый параметр насадки имеет свой энергетический оптимум, у насадки — цеолиты при у=1,25, е_ц=0,56, V=0,6м/с, р=2500 кг/м³, E=2.39 , что на 30% выше Е гальки, что говорит о более высокой энергоэффективности пористых тел.

Выводы

Разработанный метод моделирования биотехнической системы (БТС) жизнеобеспечения молочных коров позволяет обосновать технические требования и рациональные режимы работы вентиляционно-отопительной установки (ВОУ). Выбор любого значения мощности ВОУ, отличного от оптимальных значений 0_вн и ф_вн , вызывает увеличение затрат по сравнению с минимальными до 8-10%.

Разработан метод создания энергоэффективной солнечной теплицы [1, 2] заключающийся в оптимально рассчитанной конструкции всех элементов теплицы, совмещенных с тепловыми аккумуляторами, что позволяет обеспечить максимальный приход солнечной радиации в отопительный период.

Разработанная методика определения теплопроизводительности пассивных солнечных систем позволила получить инженерные уравнения расчета температуры внутри теплицы по сезонам года.

Разработан экспериментально-статистический метод расчета энергоэффективности тепловых аккумуляторов с теплоаккумулирующими насадками. В результате получено уравнение, учитывающее влияние семи переменных на количество аккумулируемого тепла, позволяющее определить наиболее оптимальный режим аккумуляции тепла в насадках. Уравнение позволяет также рассчитать оптимальную геометрию слоя: высоту Н , поперечное сечение аккумулятора F , что ранее в уравнениях энергетического баланса не учитывалось.