Энергоёмкость механического диспергирования

Использование описанной в [1] методики истирания образца абразивом позволяет с достаточной и стабильной точностью определять работу по превращению единицы массы образца в порошок. Эта величина (удельная энергия диспергирования) определена для шестнадцати чистых металлов [2] и имеет для каждого из них своё значение. Она меняется от 11,2 МДж/кг и 5,90 МДж/кг для титана и кремния до десятых долей этих же единиц для кадмия и свинца – 0,656 и 0,245. Все прочностные (механические) свойства титана и кремния существенно выше, чем у остальных металлов, поэтому естественно, что для превращения их в порошок требуется в десятки раз большая энергия.

Вместе с тем, порядок обсуждаемой величины представляется неоправданно большим: такая энергия тратится при сублимации, т.е. при разделении вещества на отдельные атомы [3]. Представляется необходимым уточнить некоторые детали проведенных экспериментов.

Большое значение удельной работы диспергирования а может быть скрыто в самом определении этой величины. За неё мы, следуя [4], приняли отношение работы против сил трения А_тр к массе вещества, превращённого в порошок. Но помимо образования порошка эта работа затрачивается ещё на деформацию вещества под той поверхностью, от которой оторвались частицы. Учитывать эту работу тем более необходимо, что энергию образования мелкодисперсной фазы из монолита (речь идёт о получении частиц порядка 100–60 мкм) определяет не процесс образования новых поверхностей, а предшествующая ему деформация [5].

Деформированный в процессе трения слой может иметь массу, которая существенно больше массы образовавшегося порошка. Учёт её может заметно изменить удельную работу в сторону уменьшения.

Убедимся в этом, сравнив два определения обсуждаемой величины:

А тр a = —— и а =

A m ₁

А тр

A m 1 + A m 2

где A m 1 - масса образовавшегося порошка; A m 2 - масса деформированного слоя.

Оценить массу деформированного слоя A m 2 можно по его толщине под поверхностью трения и площади образца. В [6] глубина проникновения деформации при трении медного образца по абразиву была найдена по уширению максимумов рентгенограмм, снятых с поэтапно стравливаемой поверхности трения. Каждый раз, помимо ширины максимумов, замеряли толщину образца. Стравливали поверхность очень осторожно, поэтому изменение толщины фиксировали интерферометром. Измерения повторяли до тех пор, пока ширина максимумов не совпадала с эталонной.

За эталон была принята ширина максимума рентгенограммы, снятой с чистой, не подвергнутой трению, поверхности отожжённого образца. Масса A m 2 поэтому существенно менее энергоёмка, нежели A m 1 : деформации в ней не доведены до разрушения и учтены даже совсем слабо деформированные слои.

Значения A m 2 оказались, вопреки ожиданиям, почти на порядок ниже, чем А т 1 . Поэтому учёт массы деформированного слоя только несколько понизил величину а , не изменив её порядок.

Это позволило нам вести дальнейшие наблюдения и расчёты без учёта массы деформированного слоя, образующегося под поверхностью трения.

Вторая причина большого значения а может быть в том, что при трении разрушается ещё и абразив, и доля энергетических затрат на образование металлического порошка может быть существенно меньше работы трения.

В результате процессов, происходящих в зоне трения, т.е. в двух трущихся телах, выделяется тепло. В него превращается порядка 96–97 % пошедшей на трение энергии [7]. Попробуем установить, как эта теплота распределяется между трущимися телами. Часть её, которая идёт на нагревание образца, можно было бы определить по изменению его температуры, массе образца m и теплоёмкости c , связанных между собой известным уравнением:

dQ = cmdT . (2)

Но не вся получаемая образцом теплота dQ_о идёт на его нагревание. Образец ещё непрерывно охлаждается, отдавая часть получаемой теплоты окружающей среде:

dQ o = dQ „ + dQ cp . (3)

Первый член уравнения найдётся по (2), если принять за dT повышение температуры в процессе трения. Для его измерения мы использовали дифференциальную термопару, один спай которой был помещён в узкое отверстие, высверленное в середине медного образца. Второй – термостатирован массивным телом, помещённым рядом с трущимся образцом, т.е. имевшим комнатную, первоначальную для образца, температуру. Показания термопары записывались автоматическим электронным потенциометром ценой деления 0,083 град/мм.

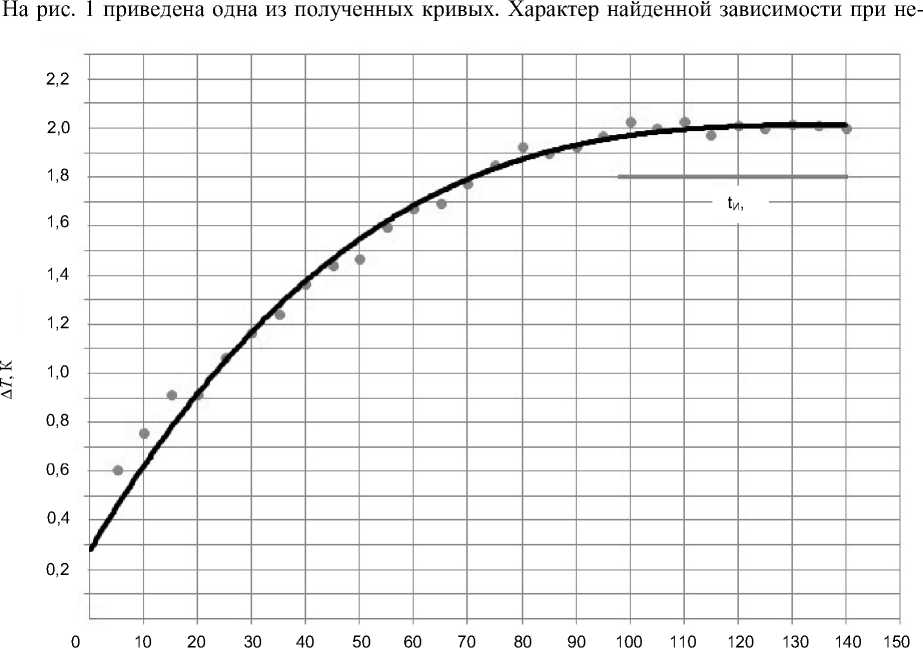
t , с

Рис. 1. Повышение температуры образца в процессе трения однократном повторении не менялся: при используемых нами скоростях трения (0,0082 м/с) повышение температуры происходит на 1,72–2,02 градуса в течение первых 85–95 сек. Далее тре-

Физика

ние становится изотермичным: температура образца T_и сохраняется постоянной в течение всего последующего трения. Наступление теплового равновесия означает, что теплота, получаемая образцом при изотермическом трении, вся отдаётся окружающей среде:

dQ o = dQ cp . (4)

Обсудим появившуюся возможность найти dQо по измерению теплоты, отданной среде. Она зависит не только от убыли температуры, как это следует из (2). Согласно уравнению Ньютона dQ ср определяется ещё соотношением температур образца и среды и поэтому меняется по мере остывания тела:

dQ cp = a S (T - T p ) dt ,

где a - коэффициент теплоотдачи; S - поверхность образца; T и T_cp - меняющаяся во времени температура образца и постоянная температура окружающей среды; t – время.

Учитывая (4), заменяя температуру образца на соответствующую изотермическому участку кривой нагрева температуру Tи и интегрируя по всему времени изотермического трения, будем иметь:

Q o = a S (Т и - Т ср ) t u ,

где tи – время изотермического трения. Его легко установить по кривой нагрева образца, запи- санной одновременно с измерением работы против сил трения (см. рис. 1).

Коэффициент теплоотдачи определяется теми условиями, в которых находится образец, зависит от его формы и размеров. Найти а можно опытным путём. Для этого интересующее нас тело следует нагреть выше температуры окружающей среды. Процесс его охлаждения будет описываться известными нам уравнениями (2) и (5). Совместное их решение даёт возможность найти одновременно ещё и площадь образца:

a S = cm

dT 1

dt (Т — Т ср ),

где – скорость охлаждения образца.

dt

Коэффициент теплоотдачи α меняется по мере понижения температуры образца Т . В (6) следует подставлять значение коэффициента при температуре изотермического трения. Тогда теплота, полученная образцом в процессе трения, будет определяться помимо его теплоёмкости и массы ещё быстротой охлаждения и временем изотермического трения:

dT

^Q o = cm ^T t u . dt

Быстроту охлаждения можно найти по углу наклона касательной к снятой на опыте кривой зависимости температуры нагретого образца от времени. Для её получения нагретый образец ставили на абразивную ленту в тот зажим, в котором он ранее тёрся. Лента теперь не двигалась, чтобы образец только охлаждался. Естественно, что при этом охлаждение образца будет происходить несколько медленнее, чем тогда, когда лента движется. Значит, значение производной, а в итоге и конечный результат, будут занижены.

Уменьшение температуры образца записывалось с помощью термопары и потенциометра, которыми мы ранее определяли повышение температуры при трении. Данные были занесены в компьютер и обработаны по программе MathCAD.

Одна из трёх полученных кривых представлена на рис. 2. Заметно, что крутизна её различна в разных точках. Касательная проведена в точке T_и , т.е. быстрота охлаждения определена при температуре изотермического трения. Среднее из трёх значений этой величины приведено в первой колонке табл. 1.

В следующих двух колонках приведены результаты трёх опытов по определению работы, совершенной за время изотермического трения и это время. Теплота рассчитана по (8). Отношение теплоты к работе меняется от опыта к опыту в пределах, соответствующих точности наших опытов. Среднее его значение приведено в нижней строке таблицы. Окончательный результат свидетельствует, что испытуемый металл трансформирует в тепло как минимум половину затраченной при трении энергии. Удельное её значение столь велико, что превращённый в порошок металл мог бы обратиться в пар. Но он, перейдя в дисперсную фазу, остался в твёрдом состоянии. Более того, кристаллическая структура его при этом сохранилась, правда несколько изменён её па- раметр [9].

<   8

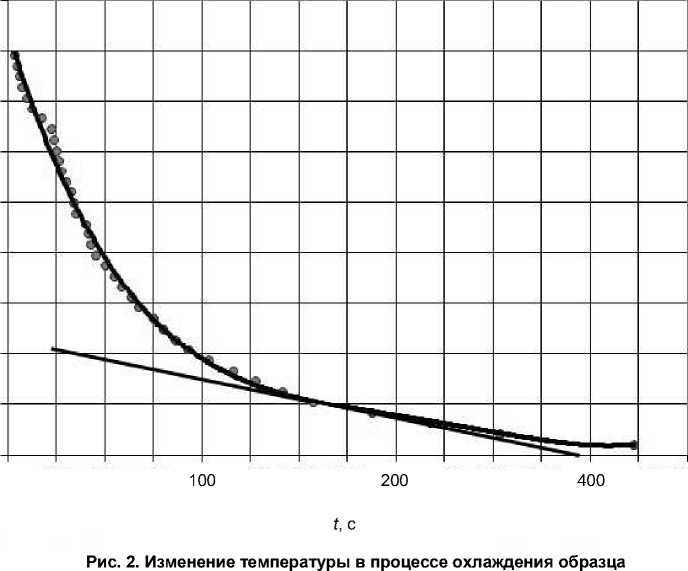
Таблица 1

Работа против сил трения и теплота, полученная образцом, за время изотермического трения

dT , град/с dt	A , Дж	tи , с	Q о , Дж	Q о / A
0,0171	2,60	39,3	1,07	0,411
	3,26	45,4	1,23	0,379
	2,32	38,7	1,05	0,454

Q_о / A =0,415 ± 0,028

Попытаемся понять этот, на первый взгляд парадоксальный, вывод. Для этого вернёмся к истокам дислокационной теории: как уже упоминалось, энергетические затраты механического измельчения металла определяют деформационные процессы [5].

Передвижение одиночного атома внутри твёрдого тела рассмотрено в [8] как совокупность процессов «испарения» и «конденсации». Первый процесс связан с затратой энергии, равной высоте потенциального барьера той ямы, в которой находился атом в положении своего равновесия. Второй приводит к сбросу полученной ранее энергии при переходе атома в новое положение равновесия. При движении дислокаций перемещается цепочка атомов. Не исключено, что движение каждого из них происходит по описанной выше схеме, а значит, связано с затратой энергии, сопоставимой с энергией связи атомов и последующим выделением её в виде тепла.

С этих позиций высокие энергетические затраты при механическом диспергировании представляются естественными: в образовавшихся частицах деформации чрезвычайно велики.

Естественна и проявившаяся связь удельной работы диспергирования с энергией связи атомов, взятой нами по [3, с. 116]. Значения этих энергий для всех изученных нами металлов представлены в табл. 2. Удельная работа для всех металлов найдена при одинаковых условиях – степени дисперсности частиц, давлении. Заметно, что сравниваемые величины не только имеют одинаковые порядки, но и одинаково меняются при переходе от металла к металлу и значения их при этом остаются сопоставимыми друг с другом.