Энергосберегающие проектные решения

Энергосберегающие проектные решения минимизируют расход топлива и обеспечиваются, прежде всего, проектированием геометрии пути, учитывающей режимы движения автомобилей и зависимость расхода топлива от дорожных условий.

ектированию энергосберегающих конструкций дороги способствует эксплуатация программ ТРАССА и КОЛОННА, достаточно точно определяющих как общий расход топлива, так и дающих для детального анализа эпюры расходов. Эпюры позволяют направленно формировать варианты проектных решений в сторону уменьшения Q , используя следующие принципы.

Один из основных принципов минимизации расхода топлива – проектирование дорожных условий, обеспечивающих эффективное использование кинетической энергии, то есть уменьшение длины участка, требующих торможения и проектирования такого сочетания элементов дороги, при котором водитель может эффективно использовать накат.

Режим наката типичен после спуска, в конце которого скорость высока и равна U 1 . Если за спуском проектируется любой элемент дороги, рассчитанный на движение со скоростью U 2 (кривым в плане, пересечение в одном уровне, съезд на площадку отдыха и т.п.) и U 2 <  U 1 , то расстояние S от этого элемента до конца спуска определяется режимом наката. Расстояние S находится решением дифференциального уравнения движения автомобиля при накате, которое имеет вид

Расход топлива пропорционален мощности двигателя, зависящей от сил сопротивления движению и скорости автомобиля, а общий расход топлива на участке дороги длиной L определяется энергией, необходимой для преодоления автомобилем этого уча-

стка, то есть

L

I

o

( kF + G a S U ( x ) 2 +

G ^f f₀ + i ( x ) + j ⁵

q ⁽ x )

Q =

V

g 7

n dx

где u ( x ) , q ( x ) , i ( x )

соответственно скорость,

удельный расход топлива и уклон как функция пути. Оптимизировать очертание продольного профиля по расходу топлива, то есть найти уравнение проектной линии, минимизирующей Q (задача вариационного

Gi + Gf + ( kF + a S GV ² + - Gdv. (2) o            p g dt

Заменив, a = i + f o , b = ( kF + a S p G ) / G , получим

5 dv a = bv =---.(3)

g dt dv dv dt dSdv

Замена — =-----= V  дает уравне- dt  dt dS dtdS ние с разделяющимися переменными, dS = -—V—- dv(4)

g a + bv ²

исчисления для одной кривой и динамического программирования для участка дороги), чрезвычайно сложно при достаточно большой длине участка и при ограничениях на величину уклонов, расстояние видимости, контрольные и рабочие отметки и т. п. Про-

a

5   v i + в с решением S =----ln-------.         (5)

2 gв   2 а

^V 2 ⁺ в

При проектировании дорожных условий в конце участков, позволяющих накапливать большую кинетическую энергию, то есть участков с высокой скоро-

¹ Авторы – соответственно профессор, доцент и аспиранты кафедры транспорта леса и инженерной геодезии

стью U 1 , следует в качестве исходных данных принимать результаты моделирования движения программой ТРАССА. При неопределенности состава потока и на стадии предпроектных разработок можно ориентироваться на таблицы 1,2, данные в которых рассчитаны по формуле (5).

Другой, не менее важный принцип, обеспечивающий сбережение энергии – проектирование продольного профиля, гарантирующего движение без переключения на пониженные передачи (I и II) особенно автопоездов и тяжелых автомобилей. При движении на этих передачах расход топлива на преодоление одного и тоже пути (по сравнению с движением на повышенных передачах), резко увеличивается по двум причинам. Во-первых, вследствие большего времени движения за счет резкого снижения скорости. Во-вторых, за счет работы двигателя на высоких оборотах, вследствие чего увеличивается удельный расход топлива (г/лс∙ч). В-третьих, за счет работы двигателя практически на внешней (не на частичной) характеристике, что тоже приводит к увеличению удельного расхода топлива

Таблица 1

Зависимость оптимальной по минимуму расхода топлива длины участка дороги от начальной и конечной скорости при i=0 % и отличном состоянии покрытия

Тип автомобиля	Начал. скорость, км/ч	Путь наката (м) при конечной скорости, км/ч
		80	70	60	50	40
ГАЗ-3110
КАМАЗ+ ГКБ	100	300	460	640	820	1000
	100	320	500	690	880	1080
ГАЗ-3110	90	150	320	490	670	860
КАМАЗ+ ГКБ	90	170	340	530	730	920
ГАЗ-3110	80		160	340	520	710
КАМАЗ+		-
ГКБ	80	-	180	360	560	740
ГАЗ-3110	70			170	360	540
КАМАЗ+ ГКБ	70	-	-	190	380	580
ГАЗ-3110	60				180	370
КАМАЗ+		-	-	-
ГКБ	60	-	-	-	190	390

Пикет, при котором водитель вынужден переходить на пониженные (I и II) передачи, определяется результатами программы ТРАССА, которая выдает на номера передач на каждом пикете при соответствующем режиме вывода результатов моделирования. Третий принцип, удовлетворяющий одновременно ряду других важных требований: безопасности, экономичности, удобства – проектирование трассы, обеспечивающей движение с постоянной скоростью. Все эти принципы легко реализуются при использовании проектировщиком в качестве индикатора энергоемкости проектных решений программ ТРАССА и КОЛОННА.

Но в переходный период от традиционной технологии проектирования к автоматизированному; а также при разработке и совершенствовании проектирующих программ можно существенно улучшить проектные решения по критерию расхода топлива, оптимизируя очертания вертикальных кривых. В пересеченной и горной местности общая длина вертикальных кривых может превысить 50 –70 %. Несмотря на периодически возрождающиеся предложения использовать в качестве вертикальных кривых клотоиды, циклоиды, параболы высоких порядков, тригонометрические кривые и т. п., проектировщики в подавляющем большинстве случаев проектируют круговые кривые и практически точно аппроксимирующие их квадратные параболы. Такое положение вызвано: во-первых, недостаточной уверенностью проектировщика в преимуществе других типов кривых перед круговой кривой (квадратной параболой), во-вторых, отсутствием практического руководства по применению других типов кривых, в-третьих, некоторым усложнением расчетов проектных отметок.

Настоящее предложение использовать кубическую параболу в качестве вертикальной кривой, обосновано соответствующим анализом, расчетами расхода топлива и методическими разработками, способствующими освоению проектировщиками энергосберегающего метода проектирования продольного профиля.

Сопоставим варианты вертикальных кривых, описанных квадратной и кубической параболами, причем схема сопряжения элементов продольного профиля такая, как показано на рисунках 1, 2.

Таблица 2

Зависимость оптимальной по минимуму расхода топлива длины участка дороги от начальной и конечной скорости при i =4 % и отличном состоянии покрытия

Тип	Началь-	Путь наката (м) при конеч-
			ной скорости, км/ч
биля	ть, км/ч	80	70	60	50	40
ГАЗ-3110
КАМАЗ+ ГКБ	100	160	240	320	390	450
	100	170	280	330	410	470
ГАЗ-3110	90	80	180	240	310	370
КАМАЗ+ ГКБ	90	90	170	250	320	380
ГАЗ-3110 КАМАЗ+	80	-	80	180	230	290
ГКБ	80	-	80	180	230	300
ГАЗ-3110	70			80	150	210
КАМАЗ+ ГКБ	70	-	-	80	150	210
ГАЗ-3110 КАМАЗ+	60	-	-	-	70	130
ГКБ	60	-	-	-	70	130

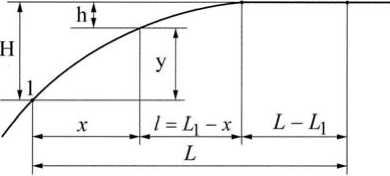
Начало координат обычно располагают в вершине кривой, т. 0, в точке 2 (квадратная парабола) или 3 (кубическая парабола).

Тогда h2 = C2l2 ,                (6)

h ₃ = C ₃ l ³ .                  (7)

Уклоны, как функции координаты l находят из ус-dh ловия i =--- и для квадратной параболы dl i = 2C21,(8)

для кубической i = 3C312.

h / i 2 г

УУ h = c\x ,L\ L-Li

Рис. 1. Сопряжение прямых с уклонами i ₁ ,i ₂ квадратной параболой

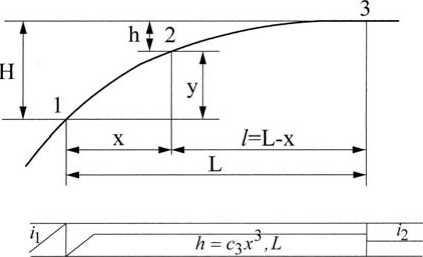
Рис. 2. Сопряжение прямых с уклонами i1 ,i2 кубической параболой Коэффициенты C2 и C3 определяются граничными условиями, в качестве которых примем: К – перепад высот точек 1 и 2, i1 – уклон в точке 1, нулевой уклон в точке 2 (или 3). Тогда

H

C 2 = ту ,            (10)

L ₁

H

Cз = Lp        dD где L1 – длина квадратной параболы от точки 1 до точки 2; L – длина кубической параболы от точки 1 до точки 3.

Так как сопоставить расходы топлива необходимо на участке одной и той же длины и так как L1 < L , дополним вариант сопряжения квадратной параболой до длины L прямолинейным отрезком нулевого уклона, длина отрезка L — L1.

Перенесем начало координат в точку 1 и тогда

Y 2 = H — h 2 = H — C 2 ( L — x ) ², (12)

Y ₃ = H — h ₃ = H — C ₃ ( L — x ) 2 .

В точке x величина продольного уклона для квадратной параболы

Y 2 = 2 C 2 ( L — x ),        (13)

для кубической

Y ₃ ' = 3 C ₃ ( L — x ) 2 .      (14)

Отметим, что при движении от точки 2 к точке 1 величина продольного уклона кубической параболы меньше, чем квадратной – таблица 3, и только на расстоянии 450 м от точки 1 уклоны сравниваются и в дальнейшем по мере продвижения к вершине уклоны кубической параболы несколько больше уклонов квадратной. Это свойство кубической параболы обеспечивает менее напряженный режим двигателя при движении по кубической параболе и как следствие эпюру скорости, показанную на рисунке 3.

Таблица 3 Уклоны и превышения квадратной и кубической параболы как функция расстояния x от точки с уклоном 60 ‰
х, м	0	200	400	600	800	900
i = y ‘ , ‰	60	40	20	0	0	0
i = y 3 , %o	60	36,3	18,5	6,7	0,7	0
h 2 , м	0	10,0	16,0	18,0	18,0	18,0
h 3 , м	0	9,53	14,9	17,3	17,9	18,0

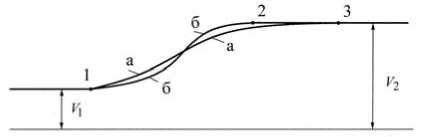
Рис. 3. Эпюры скорости: а – при квадратной параболе, б – при кубической параболе

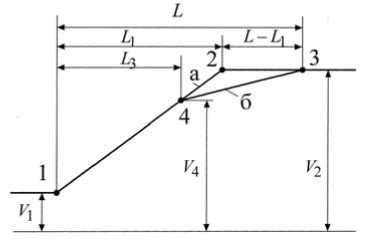
Рис. 4. Аппроксимация эпюр скорости: а – при квадратной параболе; б – при кубической параболе Для упрощения вычислений эпюры скорости аппроксимированы линейными отрезками так, как показано на рис. 4, 5, т. е., в соответствии с закономерностью взаимного соотношения уклонов кубической и квадратной параболы. В частности, при i2 = 0 получается такое соотношение между элементами кривых и эпюр скорости и расхода топлива

L i = 3 L , L 3 = 2 L ,

v 4 = 4 ⁽ v 2 - v i ^{) +} v i ,

q 4 = 4 ⁽ q 2 - q ^{) +} q 2

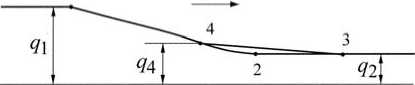
Рис. 5. Аппроксимация эпюр удельного расхода топлива: а – при квадратной параболе; б – при кубической параболе

Из общего расхода топлива Q на участке длиной L выделим части, определяющиеся квадратом скорости Q_v , величиной уклона Q_i , сопротивлением качению

Qf и сопротивлением инерции Qj . Анализ показывает, что кубическая кривая обеспечивает сбережение энергии и расхода топлива. Положительны разности: ДQv = Qv2 — Qv3 - за счет того, что в вершине подъема при квадратной параболе от точки 4 до точки 2 и далее до точки 4 скорости (а значит и расход топлива) несколько выше, чем для кубической параболы; ДQi = Qi2 — Qi3 - за счет того, что от точки 1

до точки 4, то есть на участке с большими значения-

ми g ( X ) уклоны i 3 ( X ) меньше i 2 ( X ) .

Одинаковы расходы топлива Q j 2 и Q j 3 , так как равны разности кинетических энергий

^G^ ⁽ v 2 2 g

-

v _i ) для обоих вариантов пути.

Отрицательная разность Д Q f = Q f 2 — Q f 3 получается за счет того, что на участке от точки 4 до точки 3 удельные расходы топлива больше для кубической параболы, чем для квадратной.

Анализ показывает, что значения ДQi и ДQf и ДQj примерно равны по абсолютной величине, на порядок меньше величины ДQv и поэтому ими можно пренебречь. Таким образом, сбережение рас- хода топлива обеспечивается в основном величиной ДQv , которую можно оценить, интегрируя функцию (kF + aSG)xv2 (x)q (x) от точки 4 до точки 3 отдельно для квадратной и отдельно для кубической парабол

Д Qv = (kF + aSG )x

V2q2(L — Li)— v4q4 2 v■ q2 (L — L3) /П e

e 0,25 ( kF + a SG ) Lq₂ u 2 .

Общий расход топлива можно определить по следующей приближенной формуле (общая длина участка L = i,5 i _i R , длина квадратной параболы).

Для оценки сбережения топлива рассчитаны значения Д Q v и Q 2 для вариантов проезда автомобилем ЗИЛ-130 квадратной и кубической параболы при различных радиусах квадратной параболы и при различных начальных уклонах. Результаты расчета показывают, что сбережение топлива по кубической кривой не менее 5 %. Замена квадратных парабол кубическими при вогнутых вертикальных кривых тоже обеспечивает положительный эффект по расходу топлива, но несколько меньше, чем для выпуклых кривых за счет меньшей длины вогнутых кривых. Самая скромная оценка показывает, что на 100 км дороги при интенсивности потока от 1000 до 5000 авт./сутки, Q_средн. = 20 л/км, относительной длине вертикальных выпуклых кривых i0 % и Д Q_omH = 3÷5 % экономия топлива составляет от 20 до 180 тыс. л. в год.

ВЫВОД

Проектирование профиля по кубической параболе наряду с экономией топлива обеспечивает менее напряженный режим движения, снижение эмоциональной напряженности водителя за счет удлинения пути от i ₁ к i ₂ и в сочетании с общепринятыми круговыми кривыми дает возможность лучшего обертывания проектной естественной поверхности земли, что уменьшает объем земляных работ и облегчает ландшафтное проектирование.