Энтропийная составляющая в уравнении Гиббса-Гельмгольца для характеризации изменения степени усвоения кулинарных блюд

Введение . Феноменологический подход в науке позволяет создавать теории для наблюдаемых явлений (феноменов), например, термодинамика в физике, где описание поведения макроскопических тел в тепловых процессах с помощью небольшого числа макроскопических параметров и некоторых функций от этих параметров оказывается достаточным для решения большого круга задач, представляющих технический интерес.

Основные положения термодинамики справедливы практически для любой системы и использование термодинамических методов (циклов и потенциалов) позволяет описывать даже сложные физические процессы.

Исследование статики тепломассообменных кулинарных процессов является базой для научно-обоснованного анализа правильности применения известных и создания оригинальных способов моделирования, проектирования и конструирования пищевых многокомпонентных смесей.

Цель исследования : определение степени усвоения пищевых компонентов организмом человека на основе термодинамического анализа кривых равновесия ингредиентов, входящих в пищевую систему до и после кулинарной обработки.

Исходя из цели исследования, становится необходимым решение следующего ряда задач: определение для кулинарных продуктов значения энтропийной составляющей при заданной влажности материала до и после переработки компонентов; определение энергии связи влаги с материалом до и после теплового воздействия; степени усвоения пищевой энергии организмом человека методами термодинамического анализа.

Объекты и методы исследования. В качестве объектов исследования являлись овощи (столовая свекла ГОСТ Р 51811-2001 «Свекла столовая свежая, реализуемая в розничной торговой сети», морковь ГОСТ Р 51782-2001 «Морковь столовая свежая, реализуемая в розничной торговой сети» и картофель свежий продовольственный ГОСТ Р 51808-2013 (ЕЭК ООН FFV-52:2010) «Картофель продовольственный. Технические условия») до и после варки на пару.

Активность воды определялась тензотер-мическим (эксикаторным) методом Ван-Бамелена, на экспериментальной установке, которая состоит из эксикатора, содержащего водный раствор серной кислоты, весов аналитических с погрешностью не более 0,1 % (второй класс точности по ГОСТ 24104-88), хро-мель-копелевой термопары ХК(L) ТП-011 с погрешностью не более 0,5 К (характеристики прибора регламентируются ГОСТ Р 8.585-2001), подсоединенной к мультиметру.

Степень усвоения кулинарной продукции организмом Кв_св определяли, получив значение энтропийной составляющей при необходимой по технологии влажности материала до и после обработки (разница энтропийных составляющих).

Исследования проводились в 3–5-кратной повторности. Результаты исследований обрабатывались современными методами расчета статистической достоверности измерений, а также с помощью компьютерных программ и являются достоверными.

Термодинамический анализ на основе обработки изотерм сорбции (десорбции), зависимости между равновесными параметрами (относительной влажностью воздуха или активностью воды и влагосодержанием продукта Aw = f( Up)) определяет не только энергию связи влаги с материалом, но и степень усвоения пищевых компонентов и калорий организмом человека, так как энергия связи влаги с сухим веществом зависит от связи молекул, частиц или фракций между собой, т. е. эти силы взаимодействия между собой и водой взаимосвязаны и в большой степени определяются энергетической энтропийной составляющей, особенно при диспергировании продукта, его механической или тепловой обработке (измельчении, варке и т. п.) [1].

Совпадает вид и характер изотерм сорбции большинства пищевых продуктов. Незначительные расхождения между численными значениями термодинамических коэффициентов массо-переноса и гигроскопических характеристик можно объяснить разными видами тепловой обработки или гидролиза сырья. Поскольку продукты животного и растительного происхождения относятся к сложным биополимерным системам, то применимы некоторые положения физической химии полимерных и белковых веществ.

В зависимости от внутримолекулярного взаимодействия углеводородных цепей, их длины, разветвленности и энергии выделяются характерные особенности сорбции. Количество характерных участков и точек перегиба на изотермах сорбции материалов обусловлено наличием ячеек, закрытых и открытых капилляров, клеточных оболочек и мицелл (поскольку присутствуют растительные компоненты), которые предполагают преобладание набухания – осмотического механизма сорбции.

В случае нахождения диапазона влагосо-держаний, лимитирующего тепломассобменный процесс в гигроскопической области, механизм массопереноса при обезвоживании определяем формой и энергией связи влаги с материалом, а также частиц или фракций между собой [2].

Энергия связи влаги с материалом:

E =

( dAF' — I^е U p )

- R • T • In A w .       (1)

Продифференцируем уравнение Гиббса – Гельмгольца:

A F = A E - T •A S (2) где - a s ; a e (соответственно изменения внутренней энергии (энтальпии) и энтропии, по Up при Р, T = const.

Получим:

dA F

— t5 Up

V p J T, P dAE —

[dUp v    p J T, P

- T •

( dA S ^

I⁶ U p J

Для получения выражения по дифференциальному изменению энтропии связанной воды, частиц или фракций друг с другом, продифференцируем это выражение по Т:

d

(dAF ^

( dAS )

— dT dUn v    p J t , P

( dAS }     | d UD v    p J t , P

d ( RT In A w ) ^

d T

II

—

UP )

\     ^{p J} T , P

Для количественной оценки характера изменений термодинамических составляющих уравнения Гиббса-Гельмгольца используем положения статики процессов взаимодействия с водой и приемы анализа изотерм сорбции для изохорно-изобарно-изотермического процесса, где

a(As ) „ _ - _ T •——- - энтропийная составляющая сво- dUp бодной энергии [4].

Характер изменения t •d(AS) свидетель-d Up ствует о значительной гибкости макромолекул, наличии полупроницаемых мембранных оболочек (клеточных оболочек, стенок мицелл) и ориентационном, структурном (иммобилизацион-ном) и осмотическом механизме их взаимодействия с водой.

Уравнение Гиббса-Гельмгольца базируется на правиле фаз Гиббса, определяющем число степеней свободы системы (число независимых параметров, которые можно выбирать произвольно, и они определяют значения всех остальных параметров): Sсс = k – f + 2, где k – число компонентов, f – число фаз.

При тепловой и механической обработке (диспергировании) системы (пищевых продуктов или смесей), на первый взгляд сохраняется число компонентов, а число подобных фаз, фракций, частиц, контактирующих между собой, возрастает, что по идее уменьшает число степеней свободы системы Sсс, однако при этом уменьшается связь между частицами, энтропия системы растет, следовательно растет и Sсс, а также степень усвоения компонентов диспергированных частиц организмом человека [3].

Этот парадокс можно объяснить тем, что k – это число переносимых компонентов, т. е., к примеру, при тонком измельчении, тепловой обработке (разваривании и т. п.) число компонентов возрастает, а перенос между подобными фазами, т. е. частицами с одинаковыми характеристиками (потенциалами) отсутствует. Иными словами, в аспекте массопереноса число компонентов при обработке материала увеличивается, а число фаз не меняется, что и приводит к росту энтропии и числа степеней свободы системы, и, как следствие, степени усвоения ценных компонентов пищевых продуктов организмом индивидуума.

Особенно отметим, что энтропийная составляющая в уравнении Гиббса-Гельмгольца для определения свободной энергии характеризует, в основном, состояние структурной, иммобили-зационной – внутриклеточной влаги, энтропия которой растет при разрушении ячеек, замкнутых микро- и макрокапилляров, клеток, что и происходит при механической и тепловой обработке пищевых продуктов [4]. При этом растет энтропия и числа степеней свободы системы, и, как следствие, степень усвоения переносимых компонентов пищевых продуктов, пищевых калорий, витаминов и другого организмом индивидуума.

Определив из полученных зависимостей для любого продукта значение энтропийной составляющей при необходимой по технологии влажности материала до и после обработки (разница энтропийных составляющих), можно определить степень усвоения переносимых компонентов пищевых продуктов, пищевых калорий (изменение калорийности), витаминов и другого организмом индивидуума, а также изменение энергетической и пищевой ценности продукта в процессе обработки.

Данная разница энтропийных составляющих позволит определить кинетические коэффициенты внутреннего и внешнего массо- и энергопереноса, а также граничные условия в процессе обработки, необходимые для решения математической модели переноса пищевых компонентов и калорий. Учитывая, что влажность продукта до и после, а также при различной степени обработки может быть варьируемой, необходимо получить кривые равновесия и их математическую интерпретацию для определения диапазонов влияющих факторов и определения коэффициентов и параметров при любой влажности и степени обработки исследуемого материала.

Учитывая, что пищевая энергетическая ценность не равна общей энергии потребляемых продуктов, степень усвоения энергии организмом можно оценить критерием (симплексом) – отношением пищевой калорийности или энтропийной составляющей в уравнении Гиббса-Геймгольца к общей энергии Гиббса, т. е.

Эу           Эу

К усв = о =            ад?

Э общ   RTI nA w + T^j-

Эу

= djF д д- д Up + 1 д Up или j^L

Если в знаменатель данных уравнений подставить разность калорийности или энтропийной составляющей продукта до и после переработки, то получим величину, характеризующую изменения степени усвоения в процессе реализации кулинарной технологии.

Результаты исследования и их обсуждение. По экспериментальным и расчетным данным построены графики изотерм сорбции картофеля, свеклы и моркови до и после тепловой и механической обработки (рис. 1).

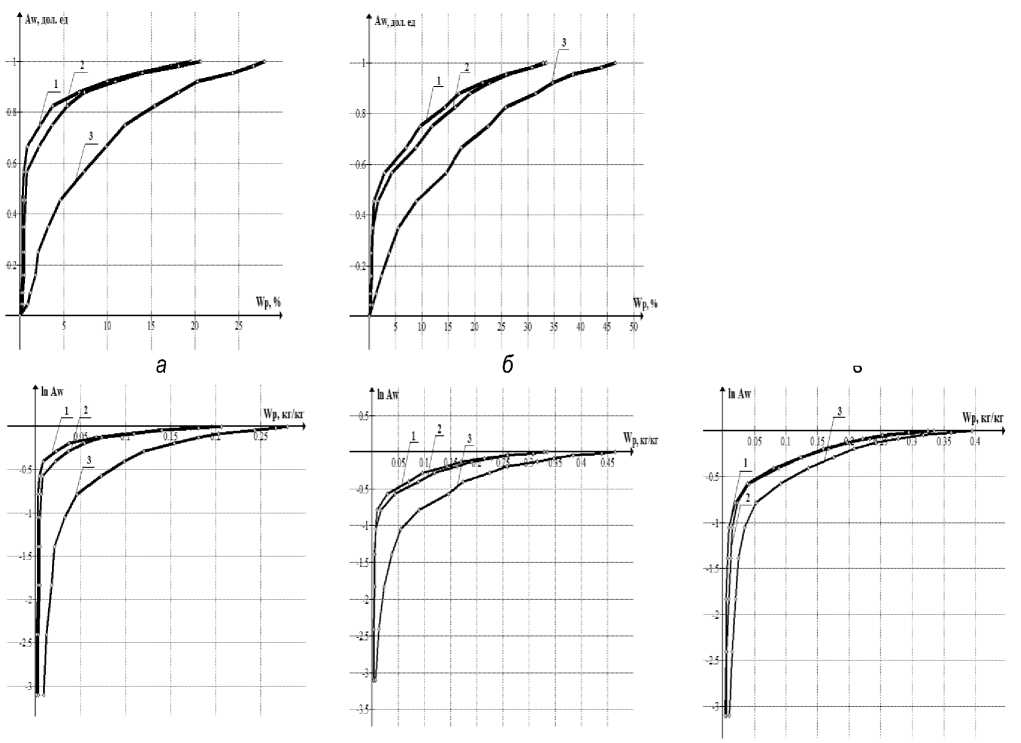
а

б

в

Рис. 1. График изотерм сорбции: а – картофеля; б – свеклы и в – моркови до и после тепловой и механической обработки при температуре 25 °С; 1 – продукт отварной измельченный;

2 – продукт отварной целый; 3 – продукт свежий

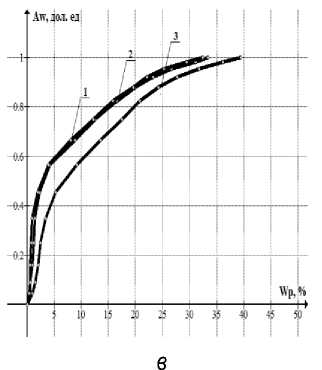
Проведена аппроксимация кривых изотерм сорбции овощей линейными уравнениями по зонам (рис. 2), что позволит получить необходимые данные для выявления закономерностей изменения калорийности продуктов в результа те обработки и степени усвоения ценных компо нентов пищи организмом человека.

к_усв для случая варки картофеля, свеклы и моркови на пару и его дальнейшей протирки (измельчение) равен соответственно 0,25; 0,30; 0,14.

Полученные данные, как и комплекс зависимостей структурно-механических и теплофизических характеристик пищевых продуктов и смесей от влияющих факторов, необходимы для физико-математического моделирования процессов обработки продуктов питания и проникновения энергетически ценных компонентов в материалы и организм индивидуума.

Термодинамический анализ может использоваться для решения вопросов устойчивости отдельных фаз и соединений, а также для установления наиболее общих закономерностей протекания энергетического взаимодействия в пищевых материалах. Выяснение последовательности перераспределения энергии, ее термодинамической вероятности в тех или иных пищевых системах помогает объяснять процессы, происходящие в системе и находить пути совершенствования технологии.

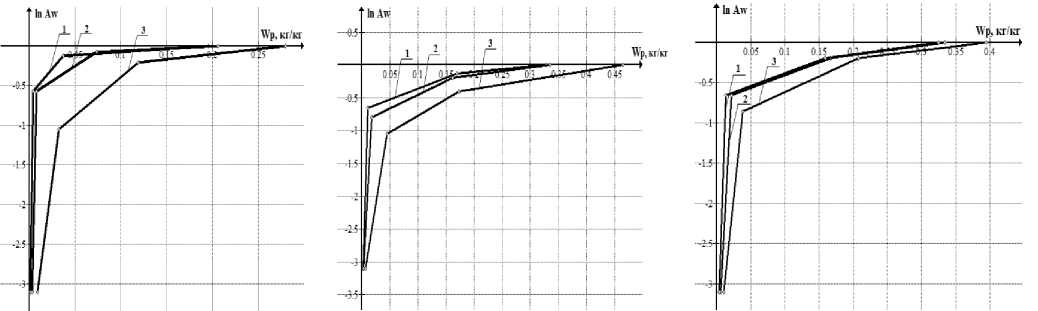
а                                 б                                  в

Рис. 2. Линейно аппроксимированные графики изотерм сорбции: а – картофеля; б – свеклы; в – моркови до и после тепловой и механической обработки при температуре 25 °С;

1 – продукт отварной измельченный; 2 – продукт отварной целый; 3 – продукт сырой

Выводы . Формализованное математическое описание технологии, направленное на создание оригинальных пищевых систем, основанное на теплофизическом и термодинамическом эк-сергетическом подходе (с учетом энтропии системы) позволит достигнуть рациональных решении поставленных задач. Ведь абстрактное понятие энтропии, как и понятие энергия, искусственно введенное, но полезное для термодинамических расчетов, стало часто использоваться не только в границах термодинамики, но и в статистике, информационных технологиях, математике, лингвистике, интеллектуальной области и др.

Термодинамический анализ может использоваться для решения вопросов устойчивости отдельных фаз и соединений, а также для установления наиболее общих закономерностей протекания энергетического взаимодействия в пищевых материалах. Выяснение последова- тельности перераспределения энергии, её термодинамической вероятности в тех или иных пищевых системах помогает объяснять процессы, происходящие в системе, и находить пути совершенствования технологии, опираясь на феноменологические исследования. Первым шагом определения последовательности и термодинамической вероятности перераспределения энергии в пищевых системах и является степень усвоения компонентов организмом человека.