Эргодические свойства стохастических динамических систем с малым шумом

В статье рассматривается влияние малого редкого шума на эргодические свойства стохастических динамических систем. Приводятся примеры, когда точные стохастические динамические системы становятся неточными, эргодические динамические системы становятся неэргодическими. Показывается, что шум обычно усиливает эргодические свойства, т. е. усиливает хаос.

Пусть X — пространство Лебега, т. е. вероятностное пространство со счетным базисом. Его можно рассматривать как отрезок [0, 1) с мерой Лебега. Стохастическая динамическая система — это четверка (X, F, р, Т), где (X, F, р,) — пространство Лебега, аТ — сохраняющее меру преобразование, т. е. это сюръективное отображение Т: X —> X такое, что УЛ Е F Т^-ХА Е F и р(Т~^хА) = р(А).

Время п есть число итераций преобразования Т. Поведение траекторий Т^лх при стремлении п к бесконечности описывается так называемыми эргодическими свойствами. Наиболее важными из них являются: неэргодичность, эргодичность, перемешивание, Х-свойство (точность для эндоморфизмов).

Сохраняющее меру преобразование Т называется эргодическим, если оно имеет только тривиальные инвариантные множества, т. е. равенство Т^-1А = А возможно только при р(А) = 0 или р^А) = 1. Равносильные условия:

• 1)    траектории точки х Е X с вероятностью 1 плотны в X [1];

• 2)    р ( J Т^пА ) = 1 УЛ Е F с р(А) > 0 [2].

\п=0    /

Сохраняющее меру преобразование Т называется перемешивающим, если

ВТ. Шарапов, 2005

Um р(Т-^пА П В) = р(А) • р(В) УЛ, В Е F.

Сохраняющее меру преобразование Т называется автоморфизмом, если оно взаимно однозначно и X^х — также сохраняющее меру преобразование.

Сохраняющее меру преобразование Т называется эндоморфизмом, если оно не взаимно однозначно. Эндоморфизм Т точный, если lim Т^пА = 1 УЛ Е F с и—too

@ р(А) > 0. Точный эндоморфизм является перемешивающим [3].

Будем говорить, что стохастическая динамическая система подвержена местному малому редкому шуму или шуму 1-го рода, если преобразование Т в отдельные моменты заменяется на другое преобразование S, мало отличающееся от Т по метрике d(S,T) = р^х : Sx + Тх\ Можно считать, что в эти моменты действует преобразование Т, а затем — преобразование S такое, что //{ж : Sx / ж} <  е для некоторого £ > 0.

Будем говорить, что стохастическая динамическая система подвержена равномерному малому редкому шуму или шуму 2-го рода, если вместо Т действует S такое, что \Sx — Тх\ < £ VieX.

Покажем, что шум может изменять эргодические свойства динамической системы. Известна лемма Рохлина — Халмоша [4]. Если Т — апериодический автоморфизм пространства Лебега (X, F, р), то V5 > 0 и Vn € N ЗЕ Е F такое, что (п—1    \

U ТгЕ ] >1-5. г=0/

Аналогичное утверждение верно и для эндоморфизмов, если перейти к прообразам V5 > 0 и Vn е N ЗЕ £ F такое, что Е, Т^Е, ..., Т~п+1Е попарно не / п—1\ пересекаются и р I |J T~lE j > 1 — 5. \i=0/

Пусть Тх = 2z(mod 1). Это точный эндоморфизм, так как lim p(TnA) = 1 VA Е Г с р^А) > 0. Возьмем £ > 0. Выберем п такое, что ^ < £. По лемме Рохлина — Халмоша, ЗЕ Е F, р(Е) = такое, что Е, Т~гЕ, ..., Т~иЛ"хЕ попарно не пересекаются и р I U Т~гЕ 1=1 — ^.

\i=0/

Определим S следующим образом: Sx = Тх на Т~ХЕ U Т~2Е U ... U Т~п+ХЕ, (п—1\

U Т~гЕ I —> г=0/

• / п-1X

• —► -^\ I U Т-гЕ I — произвольный автоморфизм, причем S действует на кп-м ша-\г=0/

ге, к = 1, со, а Т — в остальных случаях. В результате все образы множества Е имеют меру ^- и не стремятся к единице. Значит, стохастическая динамическая система не точная.

Пусть Тх = х + ce(mod 1), а — иррациональное. При этом отображении траектория всякой точки х Е X = [0,1) плотна в X, Т — эргодическое. Фиксируем малое £ > 0 и большое натуральное число т. Пусть по — наименьшее число, для которого Т^п°0 = noa(mod 1) находится на расстоянии, меньшем £ от какого-нибудь числа вида ^, 0 <  к < m — 1. Тогда на (по + 1)-м шаге действует равномерный шум: Sx = х + ^ — n₀a(mod 1). Тогда ST^O = ^. Отсюда видим, что опять через п₀ шагов действует S и ST^ST⁴⁰ = ^(mod 1). Очевидно, что траектория точки 0, а значит и каждой точки пространства X имеет пот точек и потому не плотна в X и, следовательно, динамическая система не эргодическая.

Пусть теперь Тх = х + ^(mod 1), m Е N, 0 < к < m — 1. В этом случае траектория каждой точки х Е X содержит m точек, динамическая система не эргодическая. Предположим, что в какие-то редкие моменты поступает малый равномерный шум Sx = х + a (mod 1), где а — случайная величина с |а| < £. Очевидно, что с вероятностью 1 а — иррациональное число. Тогда траектория будет плотной и динамическая система становится эргодической.

2т (mod       0 < т < ^

2т (mod ~) , j < т < 1.

Это эргодическое неточное преобразование, так как lim Тп [О, I) = | (неточ-П—*оо   12/2

ОО\ ность) и lim р, п—+ОО

(J ТпА ) = 1 VA с р(А) > 0. Если действует шум 1-го рода, так 71=0/ что меняются местами два отрезка [а,, ^], г = 1,2 равной меры и общей меры меньше е > 0, то если эти отрезки расположены так, что

[«1,6i] С

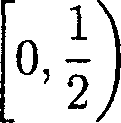
[О2>^2] С

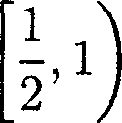
то стохастическая динамическая система становится точной, так как в этом случае мера образа любого множества положительной меры стремится к единице. Если

[oi,Ь1], [«2, 62] С

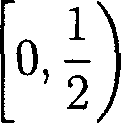
(или

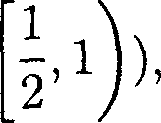
т. е. входят в одну половину одновременно при каждом шуме, то динамическая система остается неточной эргодической.

Пусть Т = < ^^Х ’ 1 3 ^{Т <} 1 • Э^то неэргодическое преобразование.

[              ± S X < £

Однако шум, описанный в предыдущем примере, превращает его либо в точную динамическую систему (при (1)), либо остается неэргодической (при (2)).

С усилением эргодических свойств: неэргодичность —> эргодичность —► перемешивание —> точность усиливаются хаотические свойства динамической системы. Из приведенных примеров видно, что ослабление эргодических свойств удается при редком жестко организованном малом шуме, а усиление эргодических свойств часто получается даже при случайном малом редком шуме. Этим объясняется, что в практических задачах динамические системы обычно принимают любые жесткие эргодические свойства.