Эвентуальная оптимальная стабилизация управляемых неоднородных систем

Решены задачи эвентуальной оптимальной стабилизации для линейных систем и оптимальной стабилизации в смысле В. В. Румянцева.

Рассматривается задача оптимальной стабилизации для линейной системы при постоянно действующих возмущениях, убывающих к нулю по экспоненциальному закону при t ^ да (t — время). При этом считается, что коэффициенты правой части управляемой системы зависят от параметра. Коэффициенты в системе предполагаются аналитическими функциями. Помимо указанной задачи здесь решается задача оптимальной стабилизации в смысле В. В. Румянцева [7] применительно также к управляемой линейной неоднородной системе. Следует отметить, что подобные задачи возникают в теории адаптивного управления (см., например, [1, § 9; 10, гл. 6]).

В данной работе задача оптимальной стабилизации сформулирована для случая, когда коэффициенты системы неточно заданы и кроме того х = 0 не является положением равновесия системы. Поэтому здесь речь идет об оптимальной стабилизации множества М - { х : х = 0 } относительно исходной управляемой системы. Таким образом, здесь рассматривается эвентуальная асимптотическая устойчивость множества М относительно исходной системы. Понятие эвентуальной асимптотической устойчивости было введено в работе [10]. В последующем вопросы эвентуальной (расчетной) устойчивости получили свое существенное развитие в работах С. В. Зубова (см., например, [2, гл. I и II]). Таким образом, в данной работе дается дальнейшее развитие теории стабилизации [1—5; 7 — 9].

Результаты настоящей работы имеют и методический интерес, так как решение задач «подводит» к рассмотрению управляемых параметрически возмущенных систем. Причем параметрические возмущения могут быть самой произвольной природы (см., например, [6]).

Рассмотрим систему х - А (е) х + В (е) м + v (t), (1) где х е Rn, и е RV, А (е) = (а^(е)) и В (е) = = (бд (е)) — соответственно (и х и) и (и х 1)

постоянные матрицы, у е С |J+ ^ J+ j и, кро ме того,

||v (t)|| <РМ ^Р2 ' ' \ t >  ф,         (2)

где (Р1 л Р2) > 0 — вещественные постоянные. Здесь a^j (е) и б,| (е) — аналитические функции переменного е в некоторой области D, принимающие вещественные значения при различных значениях параметра е, здесь dx х = —, г, 1 = 1, и.

dt

Для системы (1) рассмотрим задачу оптимальной стабилизации при условии, что минимизируется функционал

ОТ .

'-I ((

^t 0

. Т

j + ( м^т, м

dt

на решениях системы (1). Верхний индекс г означает транспонирование.

Теорема. Предположим, что при некотором ео е D rangK = |в(е0),А(е0)В(е0), ...,

А " '( е ₀) В ( е₀| = и.

Тогда можно найти р -окрестность точки е = е о, т. е. |е - е о < р , такую, что задача эвентуальной оптимальной стабилизации разрешима в р -окрестности параметра е о . При этом оптимальная функция Ляпунова V⁰(t, х, е - Е о ) и оптимальное управление разлагаются в степенные ряды по е-е о , равномерно сходящиеся в р -окрестности параметра е о .

Доказательство. Пусть ц = £ - £0- Тогда v ..кДк)   ,^(0)

^i/ (б) = Г И ^г/ , ^г/  = ^ij (б0 ) ■ к=0

Ьц ^{( 6 )} = I И ^кЬ^, $ = Ь_й ( s ₀ ^{) ,} к = 0                            (4)

г, / = 1, и.

С учетом соотношений (4) система (1) будет иметь вид где верхний символ s = 0, 1, 2 указывает на порядок формы относительно х е В”, т. е. У(2)(х) — квадратичная форма, y(1)(t, x) — линейная форма с коэффициентами, зависящими от времени t, которые являются в свою очередь непрерывно дифференцируемыми функциями, а y0(t) — скалярная непрерывно дифференцируемая функция. Будем искать решение системы (7) в виде

v

У ( t , х, и ) = Г цМ^{6 )} ( t , х ) + У ^{( 0 )} ( t ) , (8) к = 0

х = Л ^{( 0 )} х + В ^{( 0 )} м + v ( t ) + + fy ( л ^{( к )} х + В ^{( к )} м ).

к = 1

где y<^k4t, х) = У ₍ к ² ₎ ⁾ ( х ) + У^ ( t, х ) , У^ ( х ) —

квадратичная форма;

У ( к ) ( ^ - ^х )

— линейная

Здесь ц играет роль малого параметра. Используя известную теорему Н. Н. Красовского об оптимальной стабилизации [4], по

форма относительно х е R" с указанными выше коэффициентами (позднее будет дана оценка на коэффициенты). Таким образом,

лучим

м ° ( t, х, ц ) = - - 1 grad _ХУ^, х) , f ц ^кВ^ I , (6) 2 ( й )

B^(k) _ вектор-столбец с индексом к . При этом оптимальная функция Ляпунова с учетом функционала (3) находится из системы [1]

У ( ² ’ ( х ) = f f ц ^к у^ ( х ) , У ^{( 1 )} ( х ) = Гг _ц ^ у ₍« х к =°      ^V *                         к =0      ^V

х ^ t , х ) . Подставив (8) в уравнения (7) и приравнивая к нулю коэффициенты при одинаковых степенях параметра ц , получим систему уравнений, из которой найдем y^(k)(t, x) и y⁽⁰⁾(t), к = 0, 1,2 ... . Эта система имеет вид:

I grad_хy ( ^{2 )} ( х ) , f Ц А^М -

I                   к = °          )

^- 1 grady ^ ² ^ ( х ) , f ц ^кВ ^ ^к * ) + (х^т, х) = °,

⁴ 1                           )

( grady^ ( х ) , Л ^{( 0 )} х ) -

- ^ ( grady^ ( х ) , В ^{( 0 )} ) + (х^т , х ) = 0.

I grad^^ ( t, х ) , Г ц ^к А*^х | -

I                    к=0)

• - ¹ | grady ^{( 2 )} ( х ) , £ ц ^ В^ |х

• 2 (                к=0       )(7)

X I grad x У ^{( 1 )} ( t , х ) , Г Ц ^кВ^ "] +

V                   к=0

+ ( grady ^{( 2 )} ( х ) , у ( t ) ) + У ^{( 1 )} ( t , х ) = 0.

( g^rad x^y ( к ² ) ⁾ ( ^х ) ^{, а ( 0 ) х} ) +

+ Г ( grad ^y ₍ к ^{2 )} _{1 )} ( ^х ) , ^{А ( и ) х} ) -

• 1    а+р=к ( а

• - г Iz (grady(UU)(х),В ^ )|х

• 4 а,р>0 V и=0

  
  

ГГ ( g^{rad y} ( p ^{2 )} y ₎ ^{( х ) , В}

(5=0 хv к = 1, 2, 3, ...

= 0,

^{У (} ° * + ( grad х У ^{( 1 )} ( к ^х ) , v ( ^t ) ) ^-

- ¹ 1 grad_xУ^ ( t , х ) , f ц ^кВ ^ ^к * | = °. 4 1                             )

Здесь y(t, x ) = y ^{( 2 )} ( x ) + y ^{( 1 )} ( t , x ) + y ^{( 0 )} (t),

(gradxУ(0)) (t, х) , А(0)х) -- j (grady(f)) (х), в(0) ) х x (grad*^ (t, x), В<°) +

+ ( gradV« ( x ) . , ( tф^Л^ = 0,

( grad_xV₍W ( t , x ) , H ^{( 0 ) x} ) +

+ E (gradV^1-u) (t, x), H(u)x) - a+P-к a

• - 1 S [ S ( gradV® „( x ) .B < " ⁾ ) Ix

• ² a , p> 0 V u= 0                             J

  x

  
  

S ( grad x VW s ( t, x ) , B ^{( s )} ) +

V^ ₌0 \            ч/J

+ ( gradV^ ( x ) , v ( t ) ) +

d y ^{( 1 )}

+ — ^k— ( t,x ) - 0, к - 1, 2, 3, ... d t ’

V ^{( 0 )} + ( grad_xV ^{( 1 )} ( t. x ) . v ( t ) ) -

" о ( ^x ) ^{- -} 1 ( g^{rad y} ( 0 ) ⁾ ( ^x ) > ^{s ( 0 )} )

при котором нулевое решение системы x = H(0)x + B(0)«0 (x)        (14)

будет асимптотически устойчивым. Полная производная по времени t от функции У ⁽²⁾ ( x ) (к = 1, 2, ...) на решениях системы (14) будет иметь вид

^Vm< ^x >U=W < ^x • .

H ^ ⁰ ^ x + B ^ ⁰ ^ « 0 ( x ) ).

Далее с учетом системы (10) (система (10) является системой, из которой собственно и определяются У ^ ^ ) ( x ) (к=1,2,...))и соотношения (15) получим систему рекуррентных соотношений

" ■' ( ^x ’I ( ,4 ) =- ( g^V® ^{( x} •

H^x + B ^ ¹ ^ M 0 ( x ) ),

[                                            to                     I

--1 grad x V^ ( t . x ) . E V ^kB ^{( k )} I - 0.

⁴ V                     к - 0         J

к - 0. 1. 2. ...

Здесь соотношения (9) — (13) есть уравнения относительно У^ ( x ) , У^ ( t , x ) и У (°-* ( t ) , а соотношения (10) — (12) являются уравнениями относительно У^ ( 1 , x ) , к = 1, 2, 3, ... .

Vg^^ = - ( gra^{d V} ( ⁽ k ² ) ⁾ ( x ) ^{, H ( 0 )} x ) -

^- s ( g^radVA^{2 )} i ₎ ( ^x ) ^{, h (} " ^{) x} ) ⁺

"= ⁰                                 (16)

a+p= k a

+ 1 S I E ( gra^dV ₍ ⁽ „ ² -" ) ( x ) ^, B ⁽ " ⁾ )x

⁴ a , p> 0 V "= 0                           J

Уф (x)   и

x

^E ( ^{grad V} ( ^{( 2} -^ ) ^{( x )} , ^{b ( s )} )] . V s- ⁰                          J

Итак, для того чтобы решить задачу оптимальной стабилизации, необходимо найти решение системы (9) — (13), т. е. найти оптимальную функцию Ляпунова У ⁽ ° ⁾ ( t , x ) , а из соотношения (6) — оптимальное управление. Уравнения (9) и (11) (случай к = 0) соответствуют уравнениям (6) — (7) работы [10, с. 75].

Итак, из уравнения (9) находится

• У (⁽ ° ² ₎) ( x ) = x ^r C ⁽ ° > x , затем с учетом системы (5) и управления

Из асимптотической устойчивости системы (14) следует, что система (16) имеет единственное решение для каждого к >  1.

Сходимость ряда У ^{( 2 )} ( x ) = E ^^кУт ( x ) к = °      ^{( )}

доказана в работе [10, § 8]. Итак, V ^{( 2 )} ( x ) существует и представляется в виде ряда по параметру. Найдем теперь   У^ ( t, х ) =

= S иМ ! ( t, х ) . Из уравнения (11) следу- & = °       ^ ^

ет, что l«(x >1 <„)

Тогда

= - ( gradV^ ( x ) , v ( ^t ))■

^V ( o ) ^{( t}’^x ) ^_

ГО

- J ( gradV^ ( ^x ( t , V ) ) ,

V ( т

d т .

Здесь x ( т , ^, t ) ,

( ^{x (} T ^ , ^t )|       - )

есть реше

ние системы (14), нулевое решение которой

асимптотически устойчиво и, кроме того, решения системы (14) удовлетворяют неравен

ству

II х ( т , ^ ,t )|| < « 1 е « ^{2 ( т} ^, т >  t,       (18)

где « 1 и а ₂ — вещественные постоянные числа.

Исходя из неравенств (18), (2) и того факта, что ^adV^ ( ^x )| ⁵ « з ||^х|| при ||х|| <  г , г — любое конечное вещественное число; « 3 >  0 — вещественная постоянная, следует, что абсолютно и равномерно относительно ||^|| <  г сходится интеграл (17). Рассуждая аналогично, получим

||grad x V^ ( t , x )| < a ' /'v « *^^ < « 4° ^ , (19)

Вектор-функция x ( т , ^ , t ) удовлетворяет неравенству (18). Следовательно, с учетом неравенства (2) интегралы (20) абсолютно и равномерно сходятся относительно ^ ( ||^|| < г , г >  0 — любое конечное). Кроме того, имеют место неравенства, включая и (19),

IS^x^ ¹ ) ( ^{t , x} )| < а 4 ^ ^{) е -} “ ' ⁾ ' ^{- t} ° ⁾ < « 4Я (₂₁) к = 1, 2, ... .

( к )         ( 6 )          „

В этих неравенствах « 4 и «у — положительные вещественные числа, t >  ф . Таким образом, все функции y ^{( 1 )} ( t, х ) , к =1,2, ... определяются однозначно. Докажем, что ряд

У ^{( 1 )} ( t , х ) = £ цМ к') ( t , х )        (22)

к =°      ' ⁾

сходится при достаточно малых значениях параметра р на множестве ||х|| <  г при t >  t 0 , г > 0 — любое конечное. Для этого воспользуемся оценками

I^ ( к ¹ ) ( ^t -x )| ^ ^ ( к ) Г,              (23)

||gradV^ ( х)|| < 2Т2Йг,        (24)

- ' и «

положительные веществен

||В ( р)|| < ^ Р ^к^ _{( к )} , к = 0, 1, 2, ... . (25)

ные постоянные, t > t°. Следовательно, для к = 0 функция y^ (t, x) найдена. Далее из системы (12) найдем v/,9 (t, x), к =1,2,.... Из системы (12) для каждого к > 1 можно выделить полную производную от функции

^у ( 4 ) ( ^t > ^х )

по времени t на решениях систе мы. Для каждого к > 1 справедливы соотно шения

Vy ^{( t} ’ ^{x )}1 _{( 14} ) = ^- ( ^{grad V}W ^{( x )} , ^{v ( t}О к = 1, 2, ... .

Отсюда

^ 6 ) ( ^{t , х} ) ⁼ " I ( sradV'^ ( ^х ( ^т >^ ) ) > V ( ^т ) ) ^ ^{т ,} к = 1, 2, ... .                 (20)

Оценки (23) — (25) справедливы, так как:

• а)    имеет место равенство

  ГО

  
  

ГО

^VW ( ^t ’ ^x ) ^{5 -} J ( 8^rad ИЗ ( ^x ( ^t’ ^ ’ ^t ) )

’

t

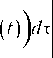
< P'kf, при 11^1 < г, г > 0 — любое конечное и неравенство (18);

• ^б)    Ущ ( х )| <  «( к )^²;

ГО

• в)    по условию теоремы ряд ^ р С В ⁶ ^

Ы0 является сходящимся в некоторой окрестности точки £0, а следовательно, существует ГО сходящийся ряд ^ pkN(k\ такой, что вы-к=0

полняется неравенство (25).

Рассмотрим далее ряд

• У ^{( 1 )} ( ц ) = г Е ц^,       (26)

к =0

который в силу условия (23) является мажорантным для ряда (22), т. е.

• У ^{( 1 )} ( t , д ) = Г ц^¹ ( t, д ).        (27)

Следовательно, для того чтобы доказать равномерную сходимость ряда (27), нужно доказать сходимость ряда (26). С помощью соотношений

Ч ) ^{( 1 ) ( t} , ^х )| =^- ( g^{rad y} ( 0 ) ^{) ( х )} ’ V ^{( t} ) )-

V ^{( 1 )} ( t , х )| = - ( gradV_t ^{( 2 )} ( х ) ,

+ 1 [ ( gra^{d V} ( ⁽ ₀ ² ) ⁾ ( х ) ^, В ^{( 1 )} ) +

V ( ^t ) ) ⁺

+ ( grad V^ ¹ ( х ) , В ^{( 1 )} ) ( grad V^ ¹ ( t , х ) , В ^{( 0 )} )

^ ^^ ^{( t}’ ^ ⁾ ( 14 ) ⁼ "  (^У^ ⁽ * ^{) - V ( t} 0 ⁺

⁺ j ^ Е ( g^fad ^Й ) ( ^х ) - ^ )( g^rad r^y ( 0 ) ( ^{t- х} ) -

B(0))j и неравенств (23) — (25) определим зависимость между Р(о), P(i), . Из первого равенства (28) с учетом неравенств (2) и (24) имеем при t > to, ||х|| < г, 0 < г = const.

Из неравенств (29) и того, что ряд

ГО

V 9 ^k R^ сходится [10, §8, 9], следует схо- 6 = 0

димость ряда (26). Далее, если учесть основные свойства степенных рядов и то, что ряд го

Е Ц^кР ( к \ сходится, получим сходящийся к = 0

го , ( к                Л ряд Е 9 I Е R(k-l)^(l) I- А следовательно, к=0    (/=0 V ряд (26) сходится. Тогда по признаку Вей-ерштрасса о равномерной сходимости степенных рядов ряд (27) будет равномерно сходящимся на множестве ||х| < г, г > 0 — произвольное вещественное число. И, наконец, учитывая (19) и (21), функция V0(t) определяется из соотношения (13).

Таким образом, оптимальная функция Ляпунова V ⁰ ( t, х, р ) в достаточно малой р -окрестности точки S 0 для системы (5) определена, значит, по формуле (6) определяется и оптимальное управление. Теорема доказана.

Рассмотрим теперь случай, когда нулевое решение системы jc = А (s0) х             (30)

асимптотически устойчиво, т. е. для системы (30) существует определенно-положительная квадратичная форма У^ (х)

такая, что

^V$( ^х)|( _{30 |} = " ^х)

где !У(0) (х) является определенно-отрицательной квадратичной формой. В этом случае для системы хс = А (s) х

| V^ ( t, х )| <  2V2^B ( o ) P i r - В ₍ о ) Г,

|v(- 1 ( t , х )| < ^ 2Т2иВ ( 1 ) Р 1 +

+ ¹ « 4 ^О)М о ) Е ^R ( 1 - 1 ) N ( 1 ) | г = ^г ,   ⁽²⁹⁾

• ²           / = 0            )

^V У б ) ( ^{t , х} )| <  ² [ V^^R ( k ) ^p 1 +

+ ^ «40)^0| Е R(i-i)N(i) |г = Rk)r’ в 5-окрестности точки S0(|s - S0 < 5) суще ствует функция Ляпунова в виде ряда

у ^{( 2 )} ( д ) = Е _о ц ^ку (⁽ ; ; ) ( д ) ,        (32)

^где ^(5 ( ^х )

есть квадратичная форма, а

9 = s - S 0 играет роль малого параметра. Пусть минимизируется функционал

+го

J = J ж ( t, х, и ) dt t o

на решениях системы (1). Поставим теперь вопрос: существует ли в (33) такая функция ж (х, u,t), для которой известная функция Ляпунова (32), решающая вопрос об асимптотической устойчивости нулевого решения системы (31), была бы оптимальной функцией Ляпунова У0 (t,х) для системы (1)?

Функцию Ляпунова в этом случае для системы (1) выберем в виде

V (t, х, ц) = ^ рМЗ (х) + h=°

■lyv (t, х) + V°) (t), h=°

k.^

где выражение ^ р^т (х) является функ-h( цией Ляпунова для системы (31); V^' (t, х) — линейные формы относительно с ограниченными непрерывно дифференцируемыми коэффициентами; У0 (t) — скалярная непрерывно дифференцируемая функция.

Составим выражение

(

В [ У, t, х, р ] = I grad_xУ ( t, х, р ) , £ р ⁶ ( Л / ^ х Х + к                     6 = 0    ^х

+ В^и ) + v ( t ) j + W to ( t, х ) + u^Tu . где

W ^{/ 2 X} ( р ,х ) + ( и^т , и ) = ж ( t,х,и ) ,

W ^{/ 2 Х} ( р , х ) = £ р М? ( х )

6=0       v 1

определенно-

положительная функция; W^ ( х ) ратичная форма, k = 0, 1, 2, ... .

квад-

Оптимальное управление определяется из уравнения (по теореме об оптимальной стабилизации [7])

I grad _хУ ( t , х , р ) , f р ⁶ В^ I + _М ° = 0. (35)

к                    6=0

Тогда критерий качества (33) будет иметь вид:

?!

/ = J I - Е P6w(6) (х)+ у I gradxy (6 x, р), to к 6=04

1 I

£ р ⁶В ( б ) I + F ( х ) + \ и^т , и ) pt. (36) 6 = 0 ) J

Здесь Р(х) есть определенно-положительная функция, которая определяется из уравнения Беллмана на оптимальном управлении, а функция У ( t , х , р ) имеет вид (34).

Теорема 2. Если нулевое решение системы (30) асимптотически устойчиво, то функция Ляпунова вида (32) будет оптимальной функцией Ляпунова для системы (1), а оптимальное управление определяется из уравнения (35).

Способ доказательства теоремы во многом схож с доказательством предыдущей теоремы. Отличие заключается в том, что здесь используется теорема об оптимальной стабилизации В. В. Румянцева [7].