Эволюция и разрушение линии роста кристалла в переохлажденном расплаве

Эти фундаментальные задачи служат теоретической основой при разработке современных технологий кристаллизации веществ в неравновесных условиях [7, 8]. При больших переохлаждениях расплава тепловые процессы в твердой фазе обладают отчетливо выраженными локальнонеравновесными свойствами, поэтому применяем модель Максвелла [9], учитывающую релаксацию теплового потока:

q + Y ^ dq/d t ) = - Agrad T .

Уравнение энергии имеет вид с (бТ/ dt) + div q = 0.

Здесь Т – температура; q – вектор удельного теплового потока; с = ρ с _p – объемная теплоемкость; ρ – плотность; t – время; γ – время релаксации теплового потока. Далее рассматриваем двухмерную задачу на плоскости декартовых координат ( x , y ). Моделируем ФГК линией сильного разрыва теплового поля. Применяем известный алгоритм [10] и выводим динамическое условие совместности на этом разрыве как следствие интегрального закона сохранения энергии. Отличительная черта изучаемых решений – учет пространственной неоднородности переохлаждения на фронте кристаллизации. Детальный анализ этого подхода к исследованию свойств линии роста представлен в [11, 12].

Цель настоящей работы – определить закономерности влияния конечного возмущения кривизны на устойчивость/неустойчивость линии роста в окрестности ее вершины.

Уравнение роста. Двухмерная фазовая граница (линия сильного разрыва) x – F ( y , t ) = 0 перемещается со скоростью N справа налево: N = N n , N < 0 (рис. 1). Координатная ось x направлена вдоль оси симметрии в сторону твердой фазы; y – поперечная декартова координата. Внутренняя нормаль n границы образует угол Ө с осью x : cos Ө = 1/ G , G = (1 + (д F/ ду)²) ¹² . Отсчет угла Ө выполняется от n в сторону оси x . Угол Ө 1 = (п/ 2) - Ө характеризует заострение линии роста и отсчитывается от оси x тоже против хода часовой стрелки (см. рис. 1). Возрастание/убывание с течением времени угла θ 1 относится к режимам затупления/заострения линии роста.

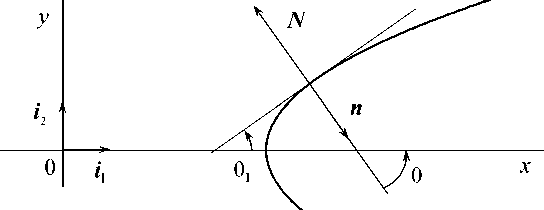
Рис. 1. Геометрические параметры линии роста

Замкнутая система трех граничных условий на фронте кристаллизации имеет следующий вид. Баланс энергии:

q j = N ( c j T j - c * T * ) + NT ( c * - C j ) - Q , Q = LL . N + ү _; d N J ,

где звездочкой отмечены параметры расплава, который находится в однородном отрелаксиро-вавшем тепловом состоянии: q ≡ 0, T ≡ const; индекс j относится к функциям, вычисленным на правой стороне сильного разрыва, в твердой фазе; qj – нормальная к границе составляющая вектора теплового потока; Tj – температура кристалла; Tc – равновесная температура кристаллизации; L – теплота фазового перехода единицы объема вещества. Теплофизические свойства расплава и кристалла считаем постоянными по обе стороны сформировавшегося сильного разрыва.

Кинетическое соотношение

I ^ = vT - T j ) , T e = T c [ 1 - ( UKL ) ] (2) определяет нормальный механизм роста из расплава. Здесь μ – кинетический коэффициент роста; U – поверхностная энергия границы раздела фаз; Т е – температура равновесия между твердой и жидкой фазами; средняя кривизна границы равна K = ( д ² ғ/ду ²)/ G ³ .

Зависимость переохлаждения ФГК от угловой координаты θ постулируем в виде

T_c - T j = ( cosO ) ⁸ B , B , 5 - const, (3) который обусловлен отклонением температуры кристалла T j от равновесного значения T c . Здесь B = T _c - T j ( Ө = 0 ) >  0; положительный параметр S характеризует пространственную неоднородность переохлаждения T c – T j . Существенно, что правая часть выражения (3) неявным образом зависит от кривизны K = дӨ/д s , где s - дуговая координата, которая отсчитывается от вершины вдоль линии роста. Дополнительные сведения, относящиеся к анализу формулы (3), имеются в

[11]. Выражения (1)–(3) составляют замкнутую систему уравнений для трех неизвестных функций N , T j , q j . Уравнение роста, определяющее зависимость F = F ( y , t ), получаем из (2), (3) с учетом формулы N = ( d FI д t ) G ¹< 0 :

д F    д ² F/ д у ²

Ф— =------г д t 1 + (дF/ ду )2

- аВ

Z ч 2 1(1—8)/2

1+ff-1

< ^д у )

.

а = L/ ( UT c ) , Ф = а/ц .

Безразмерные и размерные уравнения записываем в одинаковой форме, взяв следующее соответствие между безразмерными и размерными величинами: x →( x / x b ), y →( y / y b ), T →( T / T b ), μ B →(μ B )/| N b |, B →( B / T b ), φ→φ y b | N b |, α→α y b T b , x b = y b =| N b | t b . Нижним индексом b отмечены масштабы величин, применяемые при обезразмеривании; | N_b | – масштаб модуля скорости ФГК.

Ясно, что ∂F/∂y = tgθ, поэтому (4) можно записать в виде дғ  дө

Ф— =аВ [cos Ө]  .(5)

д t    ду

Модуль скорости перемещения линии роста и ее кривизна выглядят так:

—

N = N_m = ц ( cos Ө )⁸ В — 1cos Ө— , K = cos Ө —.

m ду J          ду

α

Ячеистая периодическая структура. Уравнение (4) при δ = 1 имеет точное решение:

F ( у, t ) = A 1 t + A ₂ ( у ) , A 1 = const <  0 ;

A ⁼ dAT = tg у ' + n n о ) , у' = у ф ( ц В + A 1 ) ;

dy

A 2 ( У ) = [ ^ ( ц B + A 1 ) J 1 ln|cos ( У ' + nn₀ )| 1 ; n ₀ = 0,1,2,...

0 < ( — A 1 ) < ц В ; N ( Ө ) = A ₁cos Ө .

Это решение представляет собой семейство стационарных контуров, расположенных на интервалах вида: n0 = 0, у' е (— л/2,п/2); n0 = 1, у' е (п/2,3п/2) и т. д. Вершины этих контуров (А = 0, А2 = 0) находятся в точках у'=пn0, а сами контуры смыкаются друг с другом при x ^ да (рис. 2). Каждая ячейка такой периодической структуры имеет конечные размеры по отношению к координате y. А именно: период yc структуры равен ус = п/ K (Ө = 0),                                       (7)

где K ( Ө = 0 ) = ф [ ц В + N ( Ө = 0 ) ] есть кривизна вершины отдельной ячейки.

Дальнейшее рассмотрение уравнения роста (5) – это построение и анализ его решений в конечных левой и правой окрестностях значения δ = 1. Будут даны примеры бифуркативных ситуаций, относящихся к переходу через порог δ = 1. Полученные аналитические результаты показывают, что по обе стороны этого порога вершина линии роста имеет клиновидную форму: y = 0, θ > 0, ∂θ/∂ y > 0. Вместе с тем заострение исходной клиновидной вершины ассоциируется с начальной стадией перехода к игольчатой форме дендрита; затупление означает переход к плоскому фронту.

Уравнение Бюргерса. Продифференцировав обе части уравнения (5) по y , получаем дифференциальное следствие уравнения роста:

ф—= cos ² Ө^Ц + а В ( 8 — 1 )( cos Ө )⁸ sin Ө— .                      (8)

д t         д у ²                        д у

Для достаточно малых углов Ө, а именно: при Ө е [0, Өе), где ӨЕ - малая величина первого порядка малости, считаем приближенно cos2 Ө^ 1, sinӨ-Ө. Например, для углов Ө = п/180; п/90; п/60 имеем соответственно 1 — cos2 Ө = 0,3046-10—3; 1,2179• 10—3; 2,7390• 10—3; 1 — (sind/d) = 0,5074 • 10—4; 2,0306x10—4; 4,5685x10—4. Следовательно, в малой окрестности Ө = 0 уравнение (8) имеет вид уравнения Бюргерса дӨ д t

¹ д 2 Ө „„дӨ _R          л

--- + р Ө — , ^р = и B ( 5 ^- 1 ) . ф д у ²     д у

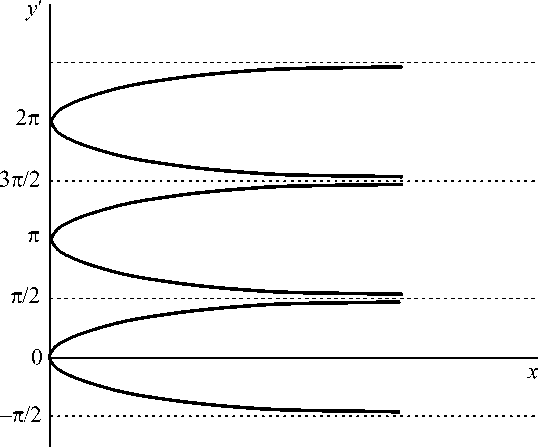
Рис. 2. Ячеистая (δ = 1) периодическая структура фронта кристаллизации

Далее рассматриваем значения 5 е ( 0,2 ] . Интересный в физическом отношении случай 5 = 3 (изолированный дендрит игольчатой формы) был изучен в [11,12] на основе уравнения (4). На рис. 3 показано влияние параметра δ на качественные свойства переохлаждения T_c – T j . Если 5 = 1, то (9) выглядит как обычное уравнение теплопроводности. По обе стороны порогового значения 5 = 1, т. е. при в < 0 и в > 0 конвективный член уравнения Бюргерса имеет разные знаки. Следовательно, если мы имеем решение Ө = Ө( у , t ) при в > 0, то формальная замена Ө ^ (-Ө) дает решение уравнения (9) при в < 0. Вопрос о физическом истолковании этих решений должен быть предметом отдельного анализа. Дело в том, что не для каждого точного решения существует нужное нам физическое содержание. В дальнейшем будем применять следующие варианты записи уравнения (9):

= h+ Ө^, h = 1 (Рф), t' = Рt, Р * 0;(10)

д t     д у²

дӨ д 2Ө „дӨ _ „    -„2

--Ө, у = рФу, t = р Фt, р *0.

д t   д у ²    д у

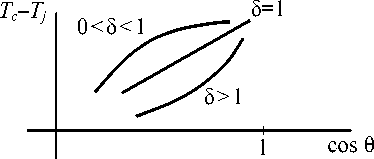
Рис. 3. Качественная зависимость переохлаждения T c –T j от параметра неоднородности δ

Для β < 0 удобно записывать θ=–Φ посредством решения уравнения дФ дt

д2 Ф    дФ „         - т

— ^+Ф , у = ^{- р} ф у , t = ^{р 2} Ф ^t .

д у ²       д у

Согласно (6) имеют физический смысл (Nm > 0, K > 0) решения Ө = Ө(у, t), удовлетворяю- щие неравенствам

0 < Ө <Ө_Е, 0 <  ( дӨ/д у ) <  аВ ( cosӨ )^{s 1}

Уравнение (9) можно рассматривать как следствие интегрального закона сохранения [13]

( ( ө dy + ^в

С     V

Ө 2    1 дӨ к _п

• 1---I dt — 0 ,

• 2   ф д у I

где С – произвольный замкнутый контур, ограничивающий область переменных ( y , t ). На основе

• (13)    выводим динамическое условие совместности на сильном разрыве y = y j ( t ), который пере-

• мещается со скоростью D = dyj/dt:

D {Ө} +

1 дӨ _о ө² — + е— ф д у 2

^ — 0 .

Здесь фигурные скобки – символ скачка функции при переходе через разрыв. В условии (14) допускаются ненулевые скачки { § } / 0, { В } / 0, т. е. { р } / 0, а для упрощения формул естественно принять { ц } — 0. Пример развернутой записи: { Ө } —Ө ⁽²) —Ө , , Ө j — Ө ( y j , t ) ; { в } — в₂ - в 1 и т. Д., где индексы «1» и «2» относятся к состояниям линии роста перед и за скачком y = y j ( t ) сответст-венно. Ясно, что сильный разрыв { ө } / 0 представляет собой излом линии роста. Если { Ө } — 0, то (14) дает непрерывную первую производную { дӨ/д у } — 0 при любом конечном D .

На разрыве (14) должен быть выполнен закон возрастания энтропии { S } >  0, где

T

S — J( c p/ T dT , c P ^}— 0.

Условие {S} — cp ln(T(2)/Tj^)> 0 дает неравенство j > Tj1 > 0, которое с учетом (3) приводит к оценке термодинамически допустимых значений параметров задачи:

0 < В ₂ ( cos Ө^,²) ) ^{5 2} < B 1 ( cos Ө^¹.                                (15)

Другой самостоятельный объект нашего исследования – волна возмущения y = y_m ( t ), т. е. слабый разрыв функции θ( y , t ). Здесь терпит разрыв первого рода первая производная по координате ∂θ/∂ y , т. е. имеем разрыв кривизны линии роста, см. (6). Этот слабый разрыв не является следствием (14), его скорость распространения dy m / dt определяется единственным образом для фиксированного фона θ = θ p ( y ) перед фронтом волны возмущения.

Во всех последующих задачах будем применять такие обозначения: Ө р — Ө p ( у — 0 ) ,

Ө ^ — Ө _р ( у ^ да ) ; у = 0, k_p = d Ө p dy ; у = 0, t = 0, k о = д Ө/ ду .

Волны возмущения и разрушения. Подстановка Хопфа [14] Ө —(2h/u)ди/ду сводит урав- нение (10) к уравнению теплопроводности ди/ дt' — h (д 2 и/ ду 2 ).

Решение и = и (у , t ‘) не зависит от перемены знака параметра в. Этот знак проявляет себя в итоговом выражении Ө( у , t '). Обсудим два примера, основанных на известных элементарных решениях уравнения теплопроводности.

Пусть и = и 1 + и ₂, и_і = a i E i , E i — exp ( hc i² 1 ' — c i- у ) , i = 1, 2; a i , c i - произвольные постоянные.

Тогда

^{Ө —— 2} h ^{( c} 1 E 1 + a 21 ^c 2 E 2 )/⁽ E 1 + a 21 E 2 ) , a 21 ^— a 2 / a .

Примем в > 0 и получим Ө > 0, если a 21 > 0, c i < 0, c ₂< 0. Волна возмущения у_т = mt ‘ , m = const > 0 распространяется по неоднородному фону

^Ө р ⁽ у ^{) —— 2 h ( c} 1 E 1 p ^{+ C} 2 a 21 E 2 p M E 1 p ⁺ a 21 E 2 p ) ,

E ip ^— exP

( h

m

—

C i ¹ у , i =1, 2; у >  0;

I

ө р =ө ( y = о, t ' = о ) , ө ; =ө ( y = о, t '^® ) =ө . .

Здесь Ө; = -2 hc1 = Ө;, если ci < c 2 < 0 либо Ө; = -2 hc 2 = Ө;, если c 2 < ci < 0. В обоих случаях 0 < Өр < ө; = Ө;, а также (dӨpIdy) ^ 0 при y ^ ∞. На вершине, в точке y = 0, имеем в начальный момент времени:

y =0, t '=0, k ₀ = 2 ha ₂₁ ( c 1 - c ₂ ) ² /( 1 + a ₂₁ ) ² ;

y =0, k_p

= k 0 ^{1 -} m ^{( c} 1 ^{+ c} 2 ) >  k

Следовательно, волна возмущения инициируется разрывом кривизны K линии роста. При t ‘ > 0 происходит заострение ( ө_; > Ө р ) исходной клиновидной вершины, т. е. уменьшается угол Ө₁, рис. 1. Кривизна на вершине клина y = +0 с течением времени уменьшается и стремится к нулю.

Решение (17) содержит произвольные постоянные a21, c1, c2, m. Приведем описание последовательности вычислений при c1< c2< 0. Задаем ӨР и Ө; >Өр, находим c1 =Ө;/(-2h); применяем вспомогательный параметр §0 е (0,1) и определяем k0 = 80 ӨР (ө; - ӨР )/(2h), а затем выбираем (независимо от ӨР, Ө;) дробь (kpIk0)>1. Теперь подсчитываем a21 =(ө; -Өр)/(өР 80), c2 = [ө; - (1 + a21 )Өр ]/(2ha21), 2m = [ө; + Өр (1 - 80 )]/[(kp /k0 )-1].

Именно разрыв производной ∂θ/∂ y обеспечивает конечную скорость m β волны возмущения. В предельном случае k p / k 0 = 1 + 0 волна уходит на бесконечность y →∞ с неограниченно большой скоростью.

Теперь рассмотрим случай, когда в (16) u = u1 + u2, u1 = a1 exp(hc21' + c1 y)+ b1, u2 = a2 exp(- yJ®/2h )

ωπ

Y = - y J — + a t + — ; a ₁, b ₁, c ₁, a ₂, ю - const.

Решение уравнения (10) имеет вид:

cos Y ,

^ ⁽ sin Y ^- cos Y )

c i ₂ E +

Ө = 2 h-------- ---.

E + cos Y + b 12 ^exp y-^^

,

E = exp hc ² 1' + c₁y + y. k

r^

' —  , a 21 = a 2 І a i , b

\2h

12 = b 1 / a 2 , c 12 = c 1 / a 21 .

Волна возмущения y_m = mt ', m = 4 2 h о > 0 распространяется по неоднородному фону

ө р

⁽ y ) = ^{2 hc}12 E p^

у

E p ⁺ 4 + b 12 ^exp y

Л

k

1    1 ’ Ep(y ) = exp(yh11),h v2 h j

hc ₁ ²

' 11 =       ^{+ c} 1 ⁺

m

Условия выполнения неравенств Ө _р > 0, d Ө _р I dy > 0, y >  0 указаны ниже. Обсудим два интересных варианта решения (18).

Вариант 1 заключает в себе следующие связи: c 2 = a ₂₁ о/ h , c 2 = 2 a ₂₁ , где c ₁ = c 0 J a/ 2 h >  0, a ₂₁ >  0 . В этом случае в области определения решения y е [ 0, y _m ] , t '> 0 имеем Ө ( y , t ) > 0 , ∂θ/∂ y > 0 при c 0 > 3,

=  (Wa+E^^^, E0 = exp(c2 п/8), co( E0 -1)

где δ 12 > 1 – вспомогательный параметр, определяющий выбор b 12 . Параметры фона такие:

ӨРӨ = [1 + (V^) + ^Г1, Ө; = 2m/c0 , kp -^/WeO/V + Co+U + b^

k ₀

c ₀[ b ₁₂ - (12) - ( b _nA/2)]

Выражение k p через c 0 , b 12 здесь не приводится: его нетрудно воспроизвести. Порядок расчетов соответствует обратной задаче, а именно: находим k 0 и k p , при которых существует априорно заданная скорость m в. Сначала задаем константу c ₀ > 3 и угол Ө р , тем самым фиксируя величину m = c ₀ Ө р /2 . Находим о = m ²/( 2 h ) ; задаем 8₁₂ > 1 и вычисляем b ₁₂, k_p , Ө p /Ө р , k_p / k 0 , а также Ө p и k 0 .

В возмущенной области (и, в частности, на вершине y = 0) экспонента E быстро подавляет колебания. Вершина клина заостряется: Ө ( y = 0, t = о ) < Ө ( y = 0, t ^ р ) , и при этом K ( y = 0, t ^р ) = 0. Своеобразие данного решения в том, что для каждого фиксированного c ₀ дробь k _p / k 0 зависит от Ө p /Ө ^р , а именно: ^ p/ k 0 ' е р Л> 0 . В этом его отличие от решения (17), в котором эти параметры независимы друг от друга и [ d ( m в )/ d ( k_p/k ₀ ) ] < 0 . Отметим еще, что при больших b ₁₂>>1 имеем ( k_p/k ₀ ) = ( с ₀ + 2 )/ ( 2 - 72 ) , и тогда для рассматриваемого режима роста скорость m e - монотонно возрастающая функция аргумента ( k_p/k ₀ ) > 1, характеризующего скачок кривизны за волной возмущения. Этот частный пример показывает, что корреляция (k_p/k 0 ) ^ ( ө p /Ө р ) может влиять существенным образом на свойства скорости волны возмущения.

Вариант 2 решения (18): c ₁ =- m/h , a ₂₁ = -1. Входные параметры: e p , е р , k p > 0. Последующие оценки и формулы расчета такие:

[1 + (1/V2 J1 < (ep/Өр)< 1; m = 2hho , b12 =

1 +   }~

.    2- J Ө'

p - 1

Iр

p

1 -

V

Ө

Ө

^ г

“ p J

k p

, о =-^

1 -

V

Ө

Ө

г

I^z p J

.

Для дальнейшего важно, что при b 12 > 0 за фронтом слабого разрыва ym = mt' получаем дӨ/дy < 0, т. е. кривизна K терпит разрыв первого рода, и еще при этом меняет знак «+» → «–». Таким образом, в начальном (t = 0) состоянии в точке y = 0 имеем предвестник расщепления клиновидной вершины: kp > 0, k0 < 0. В данном случае |k01 = kp [b12 (4 - V2)+1 + 3^2 ]/22 . Волна ym = mt' пред ставляет собой волну разрушения линии роста; ее скорость равна β 2h ω . Величину |k0| можно назвать параметром разрушения. Действительно, если kp = 0, то |k0| = 0, и разрушение отсутствует. Другой предельный случай: если (Өр ^pp ) = 1 - £, где £ > 0 малое число, то |k0|~kpс-1, m~ г-1 ,Jkp . Следовательно, при ε → 0 неограниченно большие значения |k0| и m характеризуют начальное (t = 0) состояние уже сформировавшегося расщепления клиновидной вершины.

Пример расчета. Для переохлажденного расплава чистого никеля имеем следующие значения теплофизических параметров: T_c = 1728 К; L = 2,14 • 10 ⁹ Дж/м³; U = 0,38 Дж/м². Возьмем Д T = 166 К; | N b | = 5,3 м/с; В = 1К; μ = 9,53 м/(К с). Обоснование выбора этих числовых значений и необходимые библиографические ссылки приведены в [12]. Такие же входные данные будем применять в последующих иллюстративных расчетах.

Пусть 8 = 1,5; Ө p /е р = 0,6. В результате получаем ф = 7,1795 4 0 4 с/м²; h = 2,9231 - 10 ^{- 6}м; в = 4,765 м/с; b 12 = 0,0607; о = k _p х 2,2097 м^-1; ( dy _m/ dt ) = m в = ^ к~_р х 17,1261-10 ^{- 3} м/с. Отсюда видно, что если, например, k p ~ 10⁶ м^–1, то ( dy m / dt ) ~ 17 м/с.

Перемена знака β и неавтомодельность. Будем рассматривать процессы роста при β < 0. Известное точное решение [15, с. 15] уравнения (12) дает выражение

-ф = Ө = ( y - a )Д t + b ) в² p t , a <  0, b >  0; a , b — const.

Волна возмущения y m = — mвt , m >  0 распространяется по неоднородному фону Ө р ( y ) = m ( y - ha )Д y + mhb ) , h i = 1/( - в ф ),

Ө p =- a/b , е ; = m , 0 < ( ""p;)< i, k ₀ = V ( bh ) ,

( kp/k о ) = 1 - ( " ?/ " » ) > 0.

Порядок расчетов соответствует обратной задаче: фиксируем m = Ө » , т. е. указываем скорость волны (- m в); задаем Ө ⁰ _р и k_p . Подсчитываем k_p / k₀ и находим к 0 ; теперь определяем b = 1/ ( hk 0 ) и a = -b Ө Р . Отличия от режима роста в > 0, (18), (19) состоят в следующем: 1)

Ө Р =Ө(у = 0, t = 0)> Ө(у = 0, t ^^) = 0 ; при t > 0 угол Ө уменьшается, угол заострения Ө 1 растет, т. е. происходит затупление клиновидной вершины дендрита, K(у = +0, t ^^) = 0; 2) теперь ска чок кривизны подчиняется неравенству 0  <  (кр / ко)  <  1, и знак производной

^d ( ^k P « о ім »!/" » )

< 0 меняется на противоположный.

Проанализируем неавтомодельное решение [15, с.16] уравнения (12):

-Ф = Ө =

- m 1

ІҒ” m 1 1 + a

(

2 th

I

- m l ^{У + Ь} m l t + a _?

- m i У - b

, a , b , m 1 - const.

Волна возмущения ym = -m 1 m2pt, m 1 > 0, m2 = b/a > 0 распространяется по неоднородному фону Өр (y) = Гm2y + m1 h (b - 2 th m2 )]^ha + (ym1 /m2)]> 0, d"p (y)/dy > 0, a > [(b - 2 thm2 )/m2 ]> 0, Ө» = m1 m2 Ө Р/ө; =[(b - 2th m 2)/ b ]< 1,

(ө:-ө0)2   к г  ө»■

.  _ \ р     р/    Рр        Рр1

p = --------- , -- = ------7

2 hm ₂th m ₂   к 0   ^Ө » -Ө Р

0< ( к_р / к ₀) <«, m 2 = 2 m ₂/ sh m ₂ , m 2 е ( 0,1 ) .

Для неавтомодельного решения (22) значение ӨР /Ө»» является пороговым при выборе m2 или, что то же самое, при выборе кр: если

(»0 "Р І' m2/(1 + m2)]< 1 ■ то кр/к0 > 1; если

Г m 2/ ( + m 2 ) ]< ( "Р /" » ) < ¹ .

то 0 < ( к_р / к 0 ) < 1. В обоих случаях д ( к_р/к ₀ )/ ә ( ө Р /Ө» )

< 0. После формального перехода m ₂^х,

m 2 ^ 0 [для конечных значений b и Ө » ] дробь к_р / к ₀ в (23) имеет вид, полученный при анализе автомодельного решения (21). Порядок расчета соответствует обратной задаче: фиксируем m 1 m ₂ = Ө » , т. е. указываем скорость волны (- m 1 m ₂в); задаем Ө Р и m ₂; последовательно находим m 1 , b , a , к_р , к_р / к 0 , к 0 .

Дадим в дополнение к (18), (20) еще один пример волны разрушения. Для β < 0 уравнение (12) имеет точное решение [15, с. 16]:

- ф = Ө = - m 1 - 2 a th [ a ( у - m ₁ t ) + b ] ; a , b , m 1 - const. (24)

Аналог этого решения при β > 0 описывает волну возмущения, имеющую такие же свойства, как в случае (17). Зависимости (24) соответствует волна y_m = - m в t , перед фронтом которой располагается неоднородный фон, имеющий положительную кривизну линии роста:

Ө p ( У ) = m 1 - 2 a th

- a в Ф У I 1 -

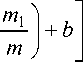
У >  У т

d Ө _p /dy >  0; m ₁> m >  0, a <  0, b >  0; 0 <  th b <  ( ө р / Ө “ ) < 1;

Ө р = m₁ - 2 a th b , ө » = m₁ - 2 a .

Вместе с тем за фронтом волны имеем ∂θ/∂ y < 0, что означает разрушение линии роста, предшествующее расщеплению клиновидной вершины. В начальном ( t = 0) состоянии предвестник разрушения находится в точке y = 0: k p > 0, k 0 < 0. Основные формулы:

thb = (1 - b1 )/(1 + b1), b1 =-в фө»-өр )2/(2| k 01), - 2 a (1 - thb )=ө»-өр,

2 Ф 1 = ^{- в} Ф ^{( ө} р ^{) 2 - ( ө} р ^{) 2} ,

• ^- р Ф ^m = k 0 |⁽ Ф 1 ^- k 0^/[(l k 0І + k_p \&» ^-ө р Л,                          ⁽²⁵⁾

• ¹    (rfi    л»^             I k 0І

^{m 1}= 2^{( ө р +ө р )-}(өда ■

Отметим, что здесь выполнено равенство k p /| k 0 | = ( m 1 / m ) – 1. Решение содержит четыре константы a , b , m ₁, m , которым соответствуют четыре входных параметра ө р , ө » , | k ₀|, к_р , и при этом оказывается, что значения | k ₀| располагаются в конечном интервале

Ф 1 ⁸ ө < | k 0І <Ф 1 ,                                           (26)

5 ө = ( ө » -ө р )/( ө » +ө р ) , 5 ө е ( 0Д ) .

Неравенства (26) получены как следствия условий m 1 > 0, 0 < th b < 1. При фиксированном k p функция m = m (| k ₀|) в (25) немонотонная, имеет максимум при

I k 0 1 = I k 0 1 _m = ^{- k}P ⁺ J^к р ^{+ ф} 1 ^kP .                                   ⁽²⁷⁾

Цепочка неравенств (26) будет выполнена для параметра разрушения (27), если кр > кр, кр = [ф1 5ө/(1 -25ө)]> 0. Отметим еще, что если 0<кр <(ф1/3), то kp <|k0|т; если кр >(Ф1/3), то кр > |к0| ^. Для дальнейшего анализа функции (25) и неравенств (26) учтем, что кр = к о 12 /(ф1 - 2| к о I m) и будем пользоваться аргументами s m, п вместо |к 01 , |к 01: т   4^0 , п»Ы2-Л£ m )(1 -S m )

^m1 = ч^{( ө} р ^{+ ө} р )—т      г,

• 2            S m + 2П(1 S m )

^{( 2 5} ө/ ^£ m ) ⁽²/ ^S m ) , ⁵ ө ^{е ( 0,1 )} , ^S m ^{е ( 0,1 )} ,

I ^к 0І m = ^S m Ф 1/ ^2, І ^к 0І =п| ^к 0І m , ^к р =Ф 1 ^е m /^{[4(1 -S} m ^{) ]} .

Здесь η = 1 соответствует точке максимума (27), а ε m = 1 – 0 характеризует предельное исходное состояние к_р ^®, | к 0І ^ ( ф ₁/2 ) , которое остается неподвижным, m ^ 0. Если 2 5_Ө /s_m >  1 , то

η = 1 не входит в физически содержательную область определения функции (28), т. е. имеем монотонное убывание: dm/дп < 0. Если 0 < (2 5ө /еm )< 1, то функция m = m(n,sm) немонотонная по отношению к аргументу п, она имеет максимум m (п = 1) = (өр + ө» )(1 - е m)/ 2. Отметим еще, что

∂m/∂εm < 0, т. е. ∂m/∂kp < 0. Такое поведение m(η, εm) отличается от режима разрушения β > 0, (18), (20), для которого скорость волны пропорциональна к^ и зависит от өр /ө» . Кроме того, решение (28) не содержит вырожденный случай kp = 0, |k0| = 0. Качественные различия между режимами разрушения при β > 0 и β < 0 дают количественные различия для скорости волны dym/dt. Порядок расчетов: задаем өр, ө»; находим 5Ө, ф1; задаем sm или, что то же самое, кр; находим k0 и границы интервала (29), в котором располагается η; выбор η означает выбор параметра разрушения |k0| и влияет на величину m.

Пример расчета: 5 = 0,5; 0 ^ = 1,8 х 10 - 2 , 0 ” = 3 х 10 - 2 ; 5_Ө = 0,25; ф і = 98,5260 1/м; s m = 0,8; |k o|_m = 39,4104 1/м; k p = 78,8208 1/м; 0,625 < n < 2,5; если П = 1, то dy m / dt = (- ^т в) = 2,2872·10^–2 м/с. Для сравнения изменим только один входной параметр: пусть ε m = 0,1. Тогда |к ₀|_т = 4,9263 1/м; k p = 0,2737 1/м; 5 < n < 20; если n = 6, то dy m / dt = (- m в) = 7,9318'Ю^-2 м/с.

Излом линии роста. Уравнение (11) имеет точное решение [14]:

Ө = 2 b /[ 1 + a exp ( - b ² t - by ) ] ; a , b - const.                          (30)

Физическое истолкование этого решения при β>0 дает такие же результаты, как в случае (17). Примем β < 0 и рассмотрим сильный разрыв (излом) вида (14), который распространяется по однородному фону Ө(1) = const: yj = Dt, D = -p2b2, ві = в2 = в < 0. Решение Ө(2)(у,t), y e [0,yj ], t > 0 дается формулой (30), содержащей константы b2 > 0, a2 e (-1,0). За фронтом излома имеем О’21 2b2/(1 + a2)> 0, кj2) = (әӨ(2)/дғ)j = a 2в2Ф(ө(27 /2, и тогда находим n- »nоГГө^п2 і^І/Lp0 зі

^{D 2}321   -^ / ²_H.¹   > ⁰ ,                   ⁽³¹⁾

_< J 7      J J/ L v ^j     7J

ө⁽ 2 ⁾=ө⁽²⁾ ( y = 0, t ^” | = 2 b ₂.

Соотношения между углами выглядят так: 0 <  Ө ” ²⁾ <  Ө - ²⁾ <  Ө ⁽¹⁾. На этих неравенствах основан порядок расчетов: задаем угол θ ⁽¹⁾ > 0, характеризующий исходный клин перед изломом, а затем выбираем соответствующие этим неравенствам углы Ө - ²⁾ и Ө ” ²⁾; подсчитываем D , см. (31). Теперь остается найти b ₂ = D /(—в г ) и вычислить a ₂ e ( - 1,0), априорно задавая k - ²² с учетом оценки 0 <  2 k ( ²⁾ <  ( Ө ( ²⁾ ) ² ( -fop ) . Отметим еще, что выпуклость излома обращена вверх, рис. 4, а, и за этим сильным разрывом происходит затупление клиновидной вершины. Предельный случай: Ө ⁽¹⁾ = Ө - ²⁾ + 0 ; излом вырождается в клин, удаляясь на бесконечность с неограниченно большой скоростью. Условие (15) возрастания энтропии будет выполнено при подходящем выборе Ө ¹^, если B ₂/ B 1 = [( 5 1 - 1 )/( S₂ - 1 )] < 1, т. е. 0 <  5₂ <  5 1 <  1.

Пример расчета. Пусть В 1 =1 К; В ₂ = 0,9 К; 5 1 = 0,5; 5 2 = 4/9; Ө⁽¹⁾ = 340^-2; O j '¹ = 2 х 10 ^{- 2}; ө ” ^{2 )} = 1 х 10 ^{- 2}. В результате получаем D = 0,1906 м/с.

Для уравнения (11) возьмем точное решение [15, с. 16]:

Ө⁽¹⁾ Е Ө ( y , t ) = - D ' + 2 a th [ a ( y - D't ) + b ] ,                            (32)

• a , b , D ‘ - const,

и на его основе рассмотрим излом, для которого в = в 1 = в 2 > 0, Ө ^{( 2 )} = О¹²¹ = const , дӨ⁽²⁾/д y = 0. Решение (32) определяет состояние линии роста перед сильным разрывом y j = D' t ', D = в D', y >  y j , t >  0 . Основные формулы:

Ө *¹) = - D' + 2 a 1 th b 1 >  0, Ө ” = Ө ⁽¹⁾ [ ( y - y j ) ^ ” ] = - D' + 2 a 1 >  0, к W = ( dO^m/d v ^ = a 1 ( 1 + th b 1 ) ( ө^{( 2 )} - Ө^У h , h = 1 ( Рф ) ,

Ө^{( 2}) -Ө⁽ 1 )         2 k J¹) h - ( ө⁽²⁾ -Ө^

a 1 =         , th b = —7,

2(1- thb)         2 kWh + (ө(2)-Ө(1))

k ( 1 ) h ^j

D ө ( ² ) -ө ⁽¹ )

- 1 ^{( ө <2)} +ө ⁽ , ‘»⁾.

y

а          y

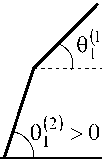
б

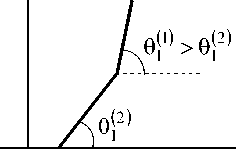
Рис. 4. Схематическое изображение углов заострения слева и справа от излома линии роста. Излом движется слева направо – от вершины на периферию

Входные параметры должны удовлетворять неравенствам:    Ө(2)>Ө*1)> 0, k !">[(’|!|)!-W]/2 h)■

и тогда а 1 > 0, 0 < th b < 1, D' > 0. Если кj¹^

не превышает указанное

пороговое значение, то излом (33) не существует. Условие (15) возрастания энтропии будет выполнено, если В 1 = В 2 , δ 1 = δ 2 . Здесь, в отличие от решения β < 0, (30), (31), излом вогнутый, рис. 4б. С течением времени исходная линия роста трансформируется в клин Ө = Ө⁽²⁾ = Ө ^,) . Предельный случай Ө ⁽²⁾ = Ө ^|1) + 0 аналогичен тому, что наблюдался для (31).

Пример расчета. В 1 = В ₂ =  1 К; 5 1 =  5 2 =  1,5; Ө⁽²⁾ =  3^10 2 ; Ө^П 2 - 10 ²;

D = к Р х 1,3928 - 10 ^{- 3} - 0,1191 м/с; к ^ >  86 1/м.

Теперь рассмотрим излом yj = Dt > 0, для которого ві > 0, в2 < 0. Состояние линии роста пе ред сильным разрывом определяется решением (32), y > yj - всем константам, входящим в эту формулу, присваиваем индекс «1». За разрывом применяем точное решение уравнения (12) вида [15, с. 15]:

Ө(2) = - b 2-- y + b 2t + a 2

y ^e[ 0, Уз ] .

Сюда входят произвольные константы а 2 < 0, b 2 < 0. Стыковка решений (32) и (34) на линии y j = Dt выполняется с помощью условия (14). Основные формулы: D = D ’ в 1 = b 2 в 2 ;

к j ')=

•-¹    =    2a     к и=

^ d y )j h 1 ch ² b 1

;- i      j j

2 , h ₂ a ₂

Һ 1 = 1 ( Р 1 ф ) , h 2 = 1 ( -в ₂ ф ) ,Ө⁽ 1 ⁾=Ө⁽¹⁾ ( y ^® , t = 0 ) = 2 a 1 - D ’, Порядок расчетов основан на цепочке неравенств: 0 < Ө ^|1) < Ө ^

Ө( 2 ) = Ө⁽²⁾ ( y = 0, t ^« ) = - b ₂.

< Ө^ ) < Ө^|,²⁾ . Сначала задаем уг-

лы Ө|P и Ө^, характеризующие начальное состояние правой части излома. Подсчитываем oSM? 1 -(J в 2 - в1в 2 /в 2 J

, определяя тем самым b ₂ и скорость D = b ₂ в₂ . Тогда D { = D /в 1 ,

2 a 1 = D { + Ө^. Задаем Ө ⁽²) и находим а ₂, b 1 :

2/ a 2 = Ө < ²⁾ - Ө^ <  0, 1 - th b = ( Ө^ - ө ' Ч ( 2 a 1 ) .

Здесь выполнено ограничение 0 < th b ₁< 1. Выпуклость излома обращена вниз (рис. 4, б ); с течением времени происходит затупление вершины клина. Условие (15) возрастания энтропии выполняется для всех B ₂<  В_х при подходящем выборе ө J P, Ө ^ . На основе формул (35) получаем

k ⁽¹⁾         R

D =^ j j -     + - ¹, k j = ^Ө -       h 2) .

Излом существует ( D > 0), если 2 k j ¹ h >  [( Ө ®)² - ( Ө ^)² ] .

Приведем два примера. Пусть В 1 = 1 К; В 2 = 0,9 К. Если Ө^ = 0,01; Ө^) = 0,012; 5 1 = 1,5; 5 2 = 0,5, то допускается излом, для которого Ө( 2 ) = 0,0294 ; Ө^ р = 0,03; D = k¹ x 6,9643 - 10 ^{- 3} - 0,0524 м/с; к W >  8 1/м; k J²⁾ = 4,904 - 10 ^{- 2} 1/м. Если Ө ⁽ _;"   0,005; Ө^ = 0,01; 5 1 = 1,01; 5 2 = 0,9, то допускается излом Ө⁽ 2 ⁾ = 0,0205 ; О¹/= 0,024; D = k Px 2,7857 - 10 —3 - 0,0357 м/с; k ^ >  13  1/м;

k *²⁾= 1,8420 - 10 ^{- 4} 1/м.

Опрокидывание линии роста. Продолжим работу с решением (32), выполнив инверсию: теперь, в отличие от излома (35), берем в і < 0, в 2 > 0. Фон перед сильным разрывом y j = Dt > 0 однородный: Ө ⁽¹⁾ = Өр = const >  0, д Ө^ ¹ /д у = 0. Левая часть излома Ө⁽²⁾ = Ө⁽²⁾( у , t ), y е[0, y j ] определяется решением (32): здесь константам a , b , D' присваиваем индекс «2». Основные формулы: 0 < О ¹² < Ө ⁽¹⁾,

Ө ⁽²⁾ ( у = 0, t ) =- D 2 + 2 a ₂ th( b₂ - a ₂ p 2 ^ D 2 1 ) , Ө { ²⁾ = Ө ⁽²⁾ ( у = 0, t = 0 ) =- D 2 + 2 a ₂ th b ₂ >  0 ; а 2 >0, b 2 >0;

к И =

( дӨ^{( 2 )}

2 a ₂

I d y J j h 2 ch ² b 2

, h 2 = 1/ (M, D = D 2 в 2 ,

D Ө ’⁴" Ө ^2,) = p +Ь Ө ) - в( Ө '¹¹)².

Своеобразие ситуации в том, что в конечный момент времени t = t ₀ > 0 имеем Ө ⁽²⁾ ( У = 0, t = 1 ₀ ) = 0, а при t >  t о начинается опрокидывание линии роста, Ө ⁽²⁾ ( y = 0, t >  1 ₀ ) <  0.

Значит, при t = t ₀ появляется предвестник втягивания внутрь носика клиновидной вершины: th ( a 2 1 ₀ ) = Ө ⁽²)/ ( 2 a ₂ - D 2 th b ₂ ) , a 2 = a ₂ в 2 ф D 2 .

Такой физический смысл данного решения обусловлен двумя обстоятельствами:  1)

Ө(1) > Ө(2) > 0, т. е. в начальном состоянии выпуклость излома обращена вверх; 2) в2 > 0, что обеспечивает условие кj2) > 0. Обращаем внимание на то, что опрокидывание происходит в левой части излома, где угол заострения Ө(2) = (п/2)-Ө(2) больше, чем в правой части, (рис. 4, а). Порядок расчетов: задаем Ө(1), Ө j2^ и кР > 0; определяем D из (36); находим D2 = D/в2 ; для вы числения а2 > 0 и th b2 е (0,1) применяем формулы

2 a 2 ² = k j ^{2 )} h , + [( D 2 + Ө <²⁾)²/2], th b 2 = ( D 2 + Ө < ²⁾)/(2 a 2 )

и подсчитываем th( a 2 1 ₀) е (0,1). Чем больше параметр кривизны kр , тем быстрее происходит опрокидывание: д 1 ₀/д( k ( ²^) <  0. Для фиксированных Ө⁽¹⁾, ff j ²', 5 1 , 5 2 всегда существует такое 0 <  В ₂<  В 1 , что (15) выполнено при t е [0, 1 ₀). Отметим, что здесь нет порога при выборе k ( ²⁾ >  0 . Данное решение, содержащее предвестник опрокидывания, можно рассматривать и при β 1 > 0, β 2 > 0, но тогда, согласно (36), условие D > 0 указывает оценку нижней границы положительных значений kр - запись не приводится.

Пример расчета: Ө⁽¹⁾ = 0,03; Ө (²⁾ = 0,02; 5 1 = 0,9; 5 2 = 1,01; В 1 = 1 К; В 2 = 0,9 К; в 1 = —0,953 м/с; в 2 = 8,53720^-2 м/с; kР = 2 - 10 ³ 1/м; D = 2,83028 м/с; а 2 = 16,5142; th b 2 = 0,9997; 1 ₀ = 1,928 - 10 ^{- 6} с.

Заключение. Для ячеистого (β = 0) фронта кристаллизации получена корреляция (7) между периодом структуры и радиусом кривизны вершины отдельной ячейки. Значение β = 0 является пороговым: по обе его стороны наблюдаются различия качественных свойств роста. Волны разрушения различаются характером зависимости скорости волны от кривизны фона: [решение (18), (20); β > 0, ∂ m /∂ k p > 0] ↔ [решение (24)–(29); β < 0, ∂ m /∂ k p < 0]. Другие различия соотносятся с режимами заострения и затупления вершины. Волна возмущения: [решения (17) и (18), (19); β > 0, заострение] ↔ [решение (21); β < 0, затупление]. Устойчивый излом: [решение (30), (31); β 1 = β 2 < 0, затупление вершины за изломом, (см. рис. 4, а )]; [решение (32); β 1 = β 2 > 0, заострение вершины за изломом, (см. рис. 4, б )]; [решение (32), (34); β 1 > 0, β 2 < 0, затупление вершины за изломом]. Таким образом, для устойчивых ситуаций (возмущение, излом) положительно-му/отрицательному значению β соответствует заострение/затупление клиновидной вершины. Неустойчивый излом – режим опрокидывания: [решение (32), (36); β 1 < 0, β 2 > 0, опрокидывание за линией излома]. Этот пример в сравнении с устойчивым изломом показывает, что важную роль играет направление перехода, которое характеризуется знаками β перед и за изломом.