Эволюция открытой космологической модели с излучением

В работе [1] с помощью подхода, позволяющего сводить космологические уравнения Эйнштейна (с тензором энергии-импульса идеальной жидкости и без космологического члена) к виду второго закона Ньютона в евклидовом пространстве, была получена открытая конформноплоская космологическая модель, описывающая эволюцию как вещества (с давлением), так и равновесного излучения. Эта модель соответствует эквивалентному «уравнению движения» для свободного осциллятора. Решение этого уравнения, возведенное в четвертую степень, есть решение гравитационных уравнений для конформно-плоской метрики в форме Фока [2], отвечающей открытой Вселенной.

Особенностью полученной модели является то, что асимптотически (при больших временах) давление определяется давлением равновесного излучения. Другими словами, при больших временах материя «расщепляется» на излучение (фоновое или реликтовое) и некогерентную пыль (вещество с нулевым давлением). Переходя еще к большим временам, получим решение Фридмана для открытой Вселенной [3].

В полученное в [1] решение входят два параметра: A и B в виде дроби A / B . Один из параметров, A , ответственен за присутствие вещества, а другой, B – за излучение.

Кроме того, функция состояния ( в = p / £ с давлением p и плотностью энергии £ ), обобщающая на эволюцию по времени понятие уравнения состояния, на всем интервале изменения времени (от начала до бесконечности) имеет характерный график с пиком вблизи начала возникновения Вселенной. В отсутствие вещества ( A = 0 ) этот пик достигает величины 1 /3, отвечающей ультрарелятивистскому состоянию (равновесное излучение).

Дальнейшее изложение будет касаться исследования поведения функции состояния, отражающего эволюцию Вселенной, и отношения A / B на всем интервале изменения параметра, связанного с физическим временем.

По поводу отношения параметров A / B можно сказать, что с одной стороны, это отношение должно быть очень маленьким, чтобы обеспечить ультрарелятивистскую фазу эволюции Вселенной (после инфляции), а с другой – на асимптотике по времени плотность реликтового излучения должна быть значительно меньше плотности вещества.

1.    Математическое описание модели

Как и в работе [1], в основу исследования кладется конформно-галилеева метрика, записанная аналогично [2]

ds ² = exp (2 а ) B 〃 v dx " dx ^v ,                                 (1.1)

с конформным множителем exp(2 а ), зависящим от переменной S , квадрат которой представляет собой произведение запаздывающего и опережающего времен в трехмерном мире:

S ² = 5 ^v x “ x ^v = t ² - r ² = ( t - r )( t + r ) = uv ; а a = a ( S ) и ^ 冲 = diag (1 ； - 1; - 1; - 1) - метрический тензор Минковского; 从 , v = 0,1,2,3 ; скорость света и гравитационная постоянная Ньютона равны единице, поэтому эйнштейновская гравитационная постоянная здесь равна к = 8 п .

Уравнения Эйнштейна без космологического члена и с источником в виде тензора энергии-импульса (ТЭИ) в приближении идеальной жидкости

(1.2)

запишутся как

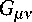
几 州 二 £ ^u 〃 u v 十 p b 〃 v ，

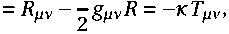
(1.3)

где £ - плотность энергии; p - давление; 4-скорость u _M = exp( a )b 乩 пропорциональна градиенту переменной S как функции координат x 〃 ： b _M = S , 乩 ; u 〃 u 〃 = 1 - условие нормировки 4-скорости; b 〃 v = u 〃 U v - g _Mv есть 3-проектор на 3-пространство, который играет роль метрического тензора для 3-пространства, при этом выполняется условие ортогональности 3-пространства и временноподобной конгруэнции u “ ： b^u “ = 0.

Далее произведем (1+3)-расщепление уравнений гравитационного поля с помощью монад-ного подхода ( [4]– [6]), что позволит записать конкретные уравнения для давления и плотности энергии, спроецированные на временноподобную мировую линию и пространственноподобную поверхность, ортогональную временноподобному направлению.

Вектор 4-скорости u µ будет использован в качестве монады, которая ортогональна 3-площадке с метрическим тензором b 〃 v = u 〃 U v - g ^v в пространстве-времени. После такой операции можно записать систему из двух дифференциальных уравнений: одно определяет плот-

ность энергии, а другое – давление.

В результате (1+3)-расщепления система уравнений (1.3) сводится к системе двух диффе-

ренциальных уравнений в полных производных после перехода к новой функции y ( S ) как

a ( S ) = 2 • ln( y ( S )) :

12 • У[y ，+ S • y ) = K£ • y

;

(1.4)

4 •卜 〃+ S y ，卜^- кр • y ⁵,

(1.5)

где штрих обозначает производную d / dS .

При построении большинства космологических моделей используется уравнение состояния, то есть связь между плотностью энергии и давлением, которая является величиной постоянной. Однако, такой подход, на наш взгляд, является препятствием к построению действительно эволюционных моделей, когда вещество (а соответственно, и уравнение состояния) меняется по мере развития таковых. Поэтому введем здесь явным образом (как это сделано в [1]) функцию состояния

伙 ^{S )}=需

Уравнение (1.5) при переходе к новой переменной х = 1/ S преобразуется к виду

(1.6)

где

d ² y

= F ⁽ x ， y ， Р )， dχ

(1.7)

F ( х ^, y ， Р ) = ^{- к} 工 • Р . ⁴ х ⁴

(1.8)

Если рассматривать χ как новую «временную» переменную, а функцию y как своеобразную «обобщенную координату», то можно интерпретировать (1.7) как уравнение Ньютона для одномерного движения частицы единичной массы под действием «силы» F из (1.8).

Такой подход позволяет исследовать класс космологических решений, для которых «сила» F является потенциальной: F = - dU / dz с потенциалом U . В частности, в [1] взят квадратичный потенциал, соответствующий колебательному движению,

где B – постоянная, имеющая в механической интерпретации смысл коэффициента жесткости пружины.

Из уравнения (1.7), которое принимает вид уравнения «колебаний», сразу получаем точное решение, приведенное как в [1], так и найденное в ( [7], [8]) более сложным путем решения уравнения Риккати:

/—             cos( B X + a )

У = ， (1 + A ²/ B ²) cos( BX + a ) =----------,                      (1.10)

cos α где tg2a = A2/B2 = 1/cos2 a + 1, A = const, B = const.

Соответствущий конформный множитель примет вид exp(2 a) =(1 + A2/B2 )2

cos⁴ ( B X + a ) = ( 1 + A 2 /B² ) ²

COs4 . (X)二           Г， cos α

(1.11)

где 9 三 B / S + a = B x + a .

Детальное исследование асимптотического поведения давления и плотности энергии для приведенного космологического решения показывают (см. [1]), что параметр A связан с массовой материей (веществом), а параметр B – с равновесным излучением. При этом с точностью O(χ5), имеем кр 之 4B2X4；

(1.12)

(1.13)

Kg 12 Ax 3(1 + 6 Ax ) + 12 B2 X4 = KEdust + KErad, где KErad = 3кр 一 плотность энергии ультрарелятивистского состояния материи, а KEdust - плотность энергии некогерентной пыли; A – параметр, входящий во фридмановское решение для открытой модели Вселенной exp(2 a) = y4

= ( 1 - A ) = ( 1 - ^A X ^{) 4},

(1.14)

совпадающего с полученным в [2].

Кроме того, так как постоянная B отвечает за наличие излучения в модели, то устремляя ее к нулю в решении (1.10), получаем в пределе решение Фридмана [1] как и при рассмотрении асимптотики решения (1.10).

2.    Функция состояния модели

Опираясь на результаты работы [1] запишем выражения для давления и плотности энергии в новых обозначениях, перейдя от х = 1/ S к новой переменной z = B / S :

KE =

4 z ⁴

^Kp = 炉

4 z ⁴ cos α

( 1 + A ²/ B ² ) ²cos⁴ 9 ( z )     ^{B 2} 〔 cos 9 ( z )

12 z ³ tg 9 ( z )(1 + z tg 9 ( z ))

^{B 2} ( 1 + A ²/ B ² ) 2 cos⁴ 9 ( z )

4;

12 z ³                       cos α ⁴

=k^{tg 9 ( z} )( 1+ ^{z tg 9 ( z} ) ) U 9z y 丿,

(2.1)

(2.2)

где 9 ( z ) = z + a .

Следовательно, функция состояния принимает вид:

e = E

1    z ctg ϕ ( z )

3 ( 1 + z tg 9 ( z ) )

(2.3)

Приравнивая функцию состояния нулю, в ( z ) = 0, получаем два корня:

π z 1 = 2 — a,

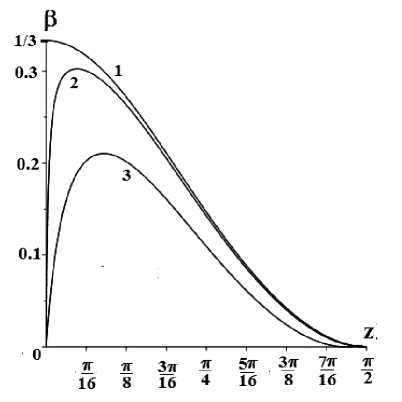
Рис. 1. Поведение функции состояния в ( z ) открытой космологической модели в случае присутствия только излучения (1) и в присутствии излучения и массовой материи (2, 3).

Первый корень z 1 отвечает наиболее близкой к началу Вселенной точке, и в отсутствии мас-π совой материи (A = 0 или tg(а) = 0) он равен z01 =万.Второй корень (z2 = 0 или S = 8) соответствует фридмановской асимптотике, когда присутствует некогентная пыль, а излучение отсутствует.

На графике рисунка 1 кривая (1) описывает поведение функции состояния в отсутствии массовой материи ( A = 0 ). Максимальное значение равно 1/3, что означает выход Вселенной на ультрарелятивистскую стадию состояния материя. В этом состоянии Вселенная после разогрева до ультрарелятивистского состояния пребывает все дальнейшее время .

Однако, как только появляется хотя бы ничтожное количество массовой материи, то сразу видим, что Вселенная не может достичь ультрарелятивистской стадии. В лучшем случае, разогрев Вселенной приведет к состоянию близком к ультрарелятивистской стадии. Это демонстрируют кривые (2), для которой tg( а 1 ) = 0.01, и (3) с tg( а 2 ) = 0.1 . Увеличение доли массовой материи означает еще, что температура с самого начала будет не очень высокой и Вселенная быстрее остынет.

Поэтому, чтобы эволюционирующая Вселенная остывала как можно медленней, необходимо, чтобы начальный разогрев выводил Вселенную как можно ближе к ультрарелятивистской стадии.

3.    Функция состояния и эволюция открытой космологической модели

Произведем инверсию переменной z , определив для дальнейшего переменную x = 1/ z = S / B . Эта операция позволяет нам «переместить» точку z 2 = 0 на бесконечность ( S = 8 ). Тогда функция состояния перепишется в виде

1   ctg 9 ( x )   _ 1    ^ctg( X 十 ^а)

..:-------------------T --- ： ------------ ： -----------.

(3.1)

(3.2)

³ ( ^X + ^tg 隼 ⁽ x )) ³ 卜 + tg( ¹¹ + а))

В этом случае корень уравнения в (x) = 0 есть п - 2 а

При отсутствии массовой материи ( A = 0 ) этот корень равен x ₀ = 2/ п .

Для проведения дальнейших исследований приведем два графика поведения функции состояния рассматриваемого решения: без массовой материи ( A = 0 ), то есть tg( а ) = 0 и при наличии

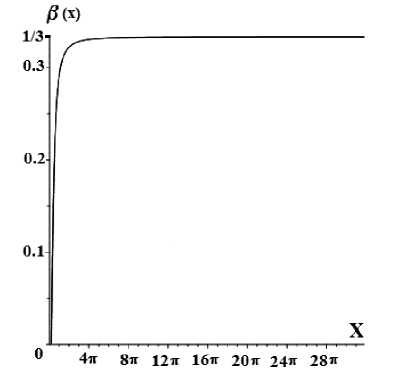
Рис. 2. Поведение функции состояния в ( x ) открытой космологической модели в отсутствие массовой материи, когда А = 0, что эквивалентно а = 0.

массовой материи.

Из графика на рисунке 2 следует, что резкий разогрев Вселенной на начальной стадии до ультра релятивистского состояния материи (это обсуждалось выше и в [9]), отмеченный на графике значением в = 1/3, в отсутствие массовой материи не спадает с течением времени, то есть нет асимптотики, присущей наличию вещества. Таким образом, Вселенная оказывается заполненной только равновесным излучением и может находиться в этом состоянии бесконечно долго.

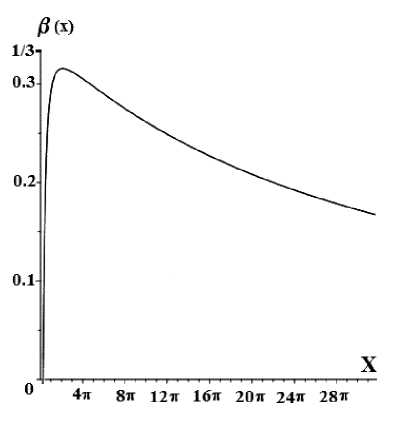
Рис. 3. Поведение функции состояния в ( x ) открытой космологической модели в присутствии массовой материи.

На графике рисунка 3 приведено поведение функции состояния при некотором значении А / B = tg( а ) = 0. Видно, что максимальное значение в не достигает ультрарелятивистской стадии в = 1/3, а оказывается меньше. После пика кривой идет резкое спадание, то есть, чем больше отношение А / B = tg( а ), тем быстрее идет остывание.

Уже эти два графика (Рис. 2–3) указывают существование зависимости между отношением параметров А / B и максимальным возможным значением функции состояния, что позволяет судить о степени разогрева Вселенной на начальной стадии.

Для нахождения такой зависимости необходимо сначала найти функцию x = x ( в ) из соотношения (3.1). Так как каждому значению x отвечает некоторое значение в ( x ), то и обозначим это значение в каждой точке как в = a из (3.1).

Пусть

Y = tg

( r^a

тогда

Отсюда получаем

c 1      1

в =--= a .

产 3 Y ( % + Y )

Y = - 2 % + £ ,9 a ² % ² + 12 a .

(3.3)

(3.4)

(3.5)

Согласно приведенным выше графикам, функция β не имеет минимумов на промежутке (2/ n <  % < 8 ) , а имеется только максимум. Поэтому, чтобы получить однозначную зависимость A / B = tg( a ) от максимального значения в = b , приравняем первую производную от функции состояния нулю и получим уравнение

2 Y ³ + zY ² + (2 - z ²) Y + z = 0,

(3.6)

где теперь точку % , соответствующему максимальному значению функции состояния, обозначим через z , то есть % ma% = z , а значение в = a заменим на b .

Подставим Y из (3.5) в (3.6), заменив a на b , приходим к уравнению

(3 b + 1) ， 3(3 b ² z ² + 4 b ) - 6 bz = 0.                               (3.7)

Решая, находим для положительных значений z :

2     1 + 3b z =--.              •

³ ^ (1 - 3 b ² - 2 b ) b

(3.8)

при условии 3 b ² + 2 b - 1 < 0, то есть b < 1/3.

Найдем tg a из (3.5) при % = z , a = b

c ( z ) - 6 b tg (丄) ^{tg a} = c ( z )tg ( z ) + 6 b

,

(3.9)

где

c ( z ) = ， 3(3 b ² z ² + 4 b ) - 3 bz .

(3.10)

Далее подставим z из (3.8) в (3.9) и получим искомую зависимость tg( a ) = A / B от максимального значения 0 ma% = b функции состояния

tg( a ) =

3 w ( b ) tg( v ( b )) + (3 b - 1) (3 b - 1)tg( v ( b ) - w ( b )

(3.11)

где

w ( b ) = 3 , (1- 2 b - 3 b ²) b ;     v ( b ) = ₂₍ *?] ) .                     (3.12)

Соответствующий график приведен на рисунке 4, где видно, что ультрарелятивистскую стадию Вселенная может достигнуть, строго говоря, при A / B = 0.

На рисунке 5 приведены графики поведения функции состояния в ( % ) для различных значений максимума b этой функции, связанного функционально с отношением параметров A / B , что продемонстрировано на рисунке 4. Кривая (1) на рисунке 5 соответствует b = 1/3 - 0.0001 ; кривая (2) - b = 1/3 - 0.001 ; кривая (3) - b = 0.2 ; кривая (4) - b = 0.05. Видно как уменьшается разогрев Вселенной с увеличением A / B .

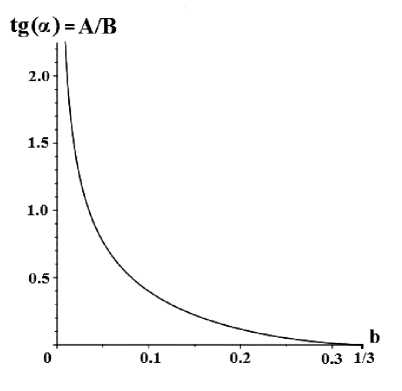
Рис. 4. Поведение отношения параметров A / B в зависимости от максимального значения b функции состояния.

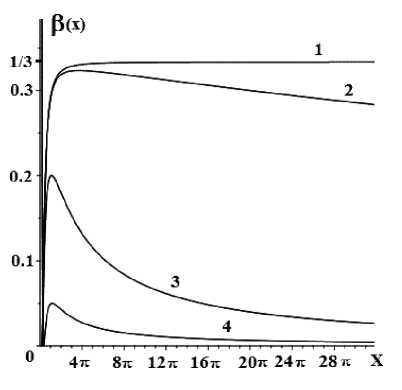
Рис. 5. Пример поведения функции состояния в ( x ) для различных значений максимума в тах = b .

4.    Оценка плотности вещества

Для проведения оценок плотностей излучения и массивной материи возьмем в нулевом приближении за параметр, отвечающий за физическое время, переменную S .

Принято считать, что в настоящую эпоху плотности массивной материи и излучения (реликтового) равны [10]:

Рmat = 2 • 10-31г/см3；     рrad = 4.45 • 10-34г/см3.

C другой стороны, согласно (1.13) эти плотности связаны с параметрами A и B как

12A    6A12

к c рmat 之行 1 + — ； к c Prad =     , где ̹ – гравитационная постоянная Эйнштейна и c – скорость света берутся в размерных единицах.

Тогда можно оценить в данной модели плотность массовой материи через оценочные значения плотности реликтового излучения и возраста Вселенной следующим образом:

P m"' " S O 7 ^Cad ^ tg ⁽ a )，                             ⁽⁴ ・ ³⁾

где S 0 – оценочная величина возраста Вселенной в настоящую эпоху, равная 13.5 млрд. лет 之 1.277 • 10²⁸ см .

Подставляя в (4.3) значение плотности излучения из (4.1) и приведенное выше численное значение возраста Вселенной, находим р ma产 1.324 • 10-31 • tg( а )(г/см3).                             (4.4)

Сравнение со справочной оценкой плотности массивной материи из (4.1) показывает, что порядок величины, стоящей перед tg( α ) в (4.4), совпадает с порядком справочного значения ρ_mat из (4.1).

Чтобы добиться полного совпадения с (4.1) необходимо, чтобы tg( α ) был примерно равен 1.510. В этом случае имеем отношение параметров A / B больше единицы, что и соответствует преобладанию массивной материи над излучением. Однако в нашей модели параметры A и B являются постоянными на всем протяжении временной эволюции модели Вселенной, то есть и вблизи начального момента возникновения Вселенной должно быть это значение A / B . Как видно из графика на рисунке 4 и формулы (3.11), такое значение A / B отвечает в тах 二 b 之 0.018 <<  1/3. Это означает, что Вселенная не будет иметь достаточного разогрева для дальнейшей длительной эволюции. Поэтому, вообще говоря, параметры A и B не должны быть постоянными за все время эволюции Вселенной.

5.    Оценка возраста Вселенной

Из всего выше сказанного следует, что кроме всего прочего параметр а (или tg( а ) = A / B ) отвечает за масштабы (размеры) Вселенной.

Если считать достоверными оценочные значения плотностей массовой материи и излучения, приведенных в (4.1) (см. [10]), то тогда можно получить приближенное выражение, связывающее отношение параметров A , B и размер Вселенной:

J 0  --[/

ρ mat

--tg( а ).

^̹ρ rad

(5.1)

Беря известные значения плотностей из (4.1), получим возраст Вселенной в световых годах

S о 之 13.5 • 10 9 • tg( а ) ( свет. лет ).

(5.2)

В итоге, численное значение, стоящее перед tg( α ), совпадает с современными данными по возрасту Вселенной. Следовательно, tg( а ) - A / B , должен быть равен примерно единице, но это означает равенство параметров A и B и противоречит тому, что настоящая эпоха – это эпоха массивной материи, а не излучения. Здесь снова напрашиваются выводы предыдущего параграфа по поводу отношения A / B .

Заключение

Исследовано ранее найденная открытая космологическая модель, полученная с помощью метода эквивалентных потенциалов. В результате показано, что эволюция и возраст Вселенной сильно зависят от отношения параметров, входящих в модель и определяющих как присутствие излучения, так и присутствие массовой материи. Кроме того, разогрев Вселенной на начальной стадии также зависит от этих параметров. Приведены иллюстративные графики, подтверждающие выше сказанное. Однако исследование показало и противоречивость введения выше указанных параметров как неизменных за все время эволюции Вселенной, так как выявилось, что вклады этих параметров за время от начала Вселенной до современной эпохи меняются на противоположные.