Эволюция размера растворимой аэрозольной частицы во влажном воздухе

Изучение взаимодействия аэрозольных частиц с влагой воздуха имеет большое значение при решении таких прикладных задач, как определение характера распространения загрязнений окружающей среды, оценка фармацевтических эффектов ингаляционного лечения, проектирование систем рудничной вентиляции соледобывающих шахт и других. При растворении веществ во влажном воздухе, в отличие от жидкости, гидратированные молекулы/ионы вещества остаются на поверхности частицы и образуют на ней слой раствора, концентрация которого меняется в процессе растворения. При этом происходит увеличение размера и массы частиц, что в свою очередь влияет на скорость коагуляции частиц и продолжительность их оседания.

Для описания гигроскопических свойств веществ в основном используются изотермы абсорбции, которые отражают зависимость равновесного размера водорастворимой аэрозольной частицы от относительной влажности воздуха [1]. Характерная картина изотермы абсорбции частицы,

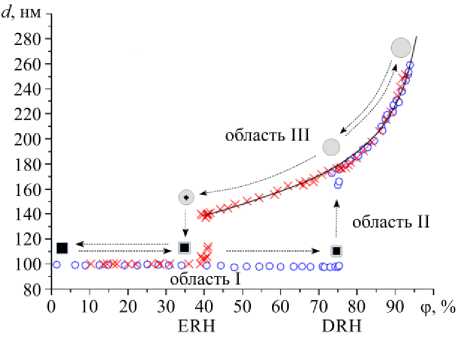
Рис. 1. Экспериментальные данные по изменению эффективного диаметра частицы NaCl при увеличении (○) и уменьшении ( х ) относительной влажности окружающего воздуха [2]; теоретическое описание процесса с помощью уравнения Кёлера (сплошная линия) [3]; кристаллическому состоянию частицы отвечают символы черного цвета, раствору – серого

предварительно высушенной и состоящей из чистого ионного кристалла хлорида натрия с начальным эффективным диаметром 99 нм, представлена на рисунке 1 (рисунок взят из работы [2]). Измерения проводились с помощью анализатора H-TDMA (Hygroscopicity Tandem Differential Mobility Analyzer) при постоянной температуре 298 К в режиме установления равновесного диаметра частицы при различных фиксированных значениях относительной влажности воздуха.

При гигроскопическом росте или уменьшении размера частицы на экспериментальных кривых можно выделить несколько областей (Рис. 1). По мере увеличения относительной влажности воздуха (область I) на поверхности растворимой частицы происходит адсорбция, в процессе которой исходный радиус сухого кристалла практически не изменяется. При достижении относительной влажностью некоторого порогового значения — гигроскопической точки DRH (Deliquescence Relative Humidity) — кристалл начинает покрываться водяной пленкой и частично растворяется в ней; на поверхности образуется насыщенный раствор. Таким образом, в области II радиус капли раствора, включающей твердое растворимое ядро, монотонно увеличивается, при неизменной относительной влажности воздуха до полного растворения. В результате формируется капля, радиус которой может в несколько раз превосходить радиус сухого кристалла. Последующее увеличение относительной влажности окружающей среды приводит к росту равновесного радиуса капли, состоящей из раствора (область III). При снижении относительной влажности воздуха радиус капли начинает уменьшаться в соответствии с участком возрастания (на области III). Однако при относительной влажности растворения DRH внутри капли твердый кристалл не появляется. Значение относительной влажности воздуха обратного фазового перехода ERH (Efflore scence Relative Humidity) ниже, чем DRH. Связано это с тем, что при отсутствии гетерогенных примесей обратный фазовый переход осуществляется в результате гомогенной нуклеации. Для образования нуклеационного зародыша новой фазы необходимо преодоление энергетического барьера. Это происходит при пересыщении раствора относительно твердой фазы в области метастабильного состояния частицы. На практике данный эффект проявляется в виде гистерезиса гигроскопических свойств частицы, то есть в несовпадении кривых гироскопического роста и испарения частиц при относительной влажности воздуха ниже величины DRH.

Объяснение характера представленной выше зависимости полностью согласуется с термодинамической теорией. Закономерность изменения размера частицы в области I с высокой степенью точности определяется из решения задачи нахождения давления насыщенного пара над каплей раствора, включающего твердое растворимое ядро [4]. Положение области II может быть установлено из условия термодинамической устойчивости капли раствора, покрывающей растворимое ядро [5]. При описании области III широко используется уравнение Кёлера [3], для которого предложены различные формы, позволяющие учитывать влияние химического состава и поверхностного натяжения частицы на ее гигроскопические свойства [6–8].

При решении многих прикладных задач наряду с информацией о равновесных состояниях требуется знание времен растворения, испарения и кристаллизации частиц, а также кинетики этих процессов. Первые работы по математическому моделированию гигроскопического роста/уменьшения частиц основывались на уравнении Максвелла для конденсации и испарения пара на/с поверхности сферической капли, неподвижной по отношению к бесконечно протяженной однородной среде:

dm dt

4 п rDjM,

^R g ^T

( Р „ - P * ) •

Здесь: m , r — масса и радиус капли; M — молярная масса воды; R — универсальная газовая постоянная; D — коэффициент диффузии пара; T — температура капли и среды; p и p — давление пара на поверхности и вдали от капли.

Широкое распространение получили модели, построенные на основе модификаций уравнения Максвелла за счет задания различных вариантов взаимосвязи давления пара на поверхности частицы с ее размером, а также благодаря учету тепловых эффектов (разделению температур частицы T и окружающего воздуха T ). Такие модели позволяют отобразить своеобразный характер кинетики испарения мелких частиц и нелинейность процесса растворения, связанную с изменением концентрации раствора в капле, а также принять во внимание изменение температуры частицы, вызываемое конденсацией/испарением молекул воды [9–11]. Однако при описании эволюции размера частицы с использованием таких моделей в большинстве случаев (см., например, в [9]) осуществляется переход от дифференцирования по массе к производной по радиусу (диаметру) частицы:

dr* _ D f M i P „ _ P *

dt   R g P [ T  T *

тем самым предполагается, что плотность частицы р = const . По мнению автора данной статьи, такой переход является некорректным вследствие того, что плотность частицы меняется в процессе растворения.

Кроме того, поскольку в таких моделях не учитывается влияние нерастворенного ядра частицы на концентрацию раствора, они не способны отображать все этапы роста/уменьшения частицы. В ряде работ, например в [11], для воссоздания фазового перехода при критической влажности DRH (область II) используется искусственное разделение уравнений на этапы до и после полного растворения кристаллического вещества частицы.

В настоящее время активно применяются многослойные кинетические модели, такие как в [12, 13] и другие, в которых за счет разделения объема частицы на слои и четкого выделения различных физических и термодинамических процессов на каждом слое, а также задания их взаимного влияния друг на друга удается воспроизвести многофакторную кинетику растворения частиц. Такие модели распространены при описании поведения многокомпонентных аэрозольных частиц, содержащих как растворимые, так и нерастворимые химически активные вещества органической и неорганической природы. На сегодняшний день наиболее полной кинетической моделью является KM-GAP модель [14], в которую заложен принцип многослойности и, помимо транспортных свойств молекул, учитываются химические реакции между компонентами частицы. Данная модель широко распространена при изучении эволюции атмосферных аэрозолей во влажной атмосфере. Обстоятельный обзор текущего состояния термодинамики атмосферных аэрозолей и моделирования их массопереноса можно найти в работе [15].

Целью настоящей работы является:

– построение на основе уравнения Максвелла уточненной модели эволюции частицы в среде водяного пара с включением фазовых переходов растворения и кристаллизации;

– верификация модели на основе известных экспериментальных данных о гигроскопическом изменении размера частиц хлорида натрия;

– оценка изменения плотности частицы в процессе растворения.

2.    Математическая модель эволюции размера

Рассмотрим воздух как смесь неконденсирующегося пассивного газа и конденсирующихся паров воды с относительной влажностью ф = P J P n ( Т „ ) , где p „ — давление пара вдали от частицы, а p „ ( Т „ ) — равновесное давление насыщенного пара при температуре окружающего воздуха. Водорастворимая аэрозольная частица, помещенная в воздушную смесь, может расти или уменьшаться в зависимости от соотношения давления пара над поверхностью частицы p. = p ( r .) и вдали от нее р, .

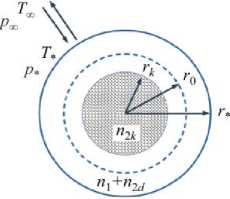
Рис. 2. Модель частицы

Для упрощения расчетов частица считается сферически симметричной с эффективным радиусом r (Рис. 2). Обозначим общее число молекул в частице как n = n + n ₂, при этом n — число молекул воды, а n₂ = n_lk + n_ld = const — число молекул растворяемого вещества, находящихся в кристаллическом ( n_2к ) и растворенном ( n ) состояниях.

Используя приближение аддитивности объемов, то есть, полагая, что общий объем растворенной частицы равен сумме объемов сухой частицы и поглощенной воды [8], установим связь между радиусом частицы и количеством молекул воды и растворенного вещества:

V = 4п r3 3 = ntvt + n2v2,

где v , v — объемы молекул воды и растворяемого вещества.

Начальное состояние частицы задается ее радиусом r₆ и мольной долей воды в частице х₁₀ = n₁₀/n , где n — количество молекул воды в частице в начальный момент времени. Отсюда имеем:

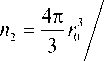
x 10

^ ( 1    ^ 10 )

^V 1 + V 2

^П 10 =

^x 10 ⁿ 2   _.

^{( 1} - ^ 10 )

Как было упомянуто выше, при помещении сухой частицы во влажный воздух сначала происходит процесс адсорбции молекул воды на ее поверхности, поэтому для определения количества растворенных молекул исходного сухого вещества в начальный момент времени n значение n сравнивается с равновесным количеством молекул воды, способных адсорбироваться на поверхности частицы при заданной относительной влажности воздуха A . Зависимость A от относительной влажности воздуха зададим уравнением изотермы полимолекулярной (многослойной) адсорбции БЭТ [16]:

A ^ = A (ф) = A n т;—vTT . ( 1 -ф ) ( 1 + ( c - 1 ) ф )

Здесь: c — отношение константы адсорбционного равновесия в первом слое и константы конденсации, который, согласно работе [17], для адсорбции молекул воды на поверхности хлорида натрия равен 1,5; параметр A — количество молекул воды, необходимых для создания монослоя вокруг сухой частицы, определяемый из соотношения:

A

n

16 | 3 n₂v ₂ Y³ d 2 ( 4 n ^J

где d — диаметр молекулы воды.

В случае выполнения неравенства n0 < Аф  все молекулы растворяемого вещества находятся в кристаллическом состоянии, то есть n 2 d 0 = 0    и    n 2 k 0 = n 2'

Если это условие не выполняется, то количество растворенных молекул вещества определяется соотношением:

n2d0 = n10K (M1 IM2 ) ,     n2k0 = n2 — n2d0'

Здесь: M , M — молярные массы воды и растворяемого вещества; K — растворимость вещества в воде (для хлорида натрия она составляет приблизительно 36 г на 100 г воды при температуре +25°С). При n_wK ( M,/M ₂) >  n ₂ частица считается полностью растворенной, что означает:

n 2 d 0   n 2’      n 2 k 0

Изменение количества молекул воды в частице происходит за счет их потока через ее поверхность. Предполагая поток диффузионным, связанным с разностью давлений газа вдали от частицы и на ее поверхности, уравнение баланса массы опишем уравнением Максвелла, которое с учетом тепловых эффектов и подстановки m = р, vn +р₂ v₂n ₂, где n₂ = const, принимает вид:

dn 1 _ 4- r * D f P n ( T „ ) I _ф dt         k b      I T „

1       J ,

T * P n ( T „ ) J

где D — коэффициент диффузии молекул воды в газе, k — константа Больцмана, T , T — температура пара на поверхности частицы и вдали от нее. Радиус частицы определяется из соотношения (3):

r _*

— ( n 1 v 1 + n 2 v 2 )    .

4 П

Как и в работе [9], при расчете давления насыщенного пара на поверхности частицы учитываются: – его зависимость от температуры в виде модификации уравнения Клапейрона–Клаузиуса:

P * ( T * ) = P n ( T „ ) exp

M Г _± - ! X R g I T   t * ^J

где L — удельная теплота парообразования/конденсации;

– его повышение за счет кривизны поверхности частицы (по формуле Томсона):

P * ( ^T* ) = P n ( ^T * ) exp

2 ^1 у । r * k b T , J ,

где c — поверхностное натяжение воды;

– его снижение благодаря присутствию в частице растворимых соединений, которое характеризуется активностью воды в растворе a :

P * ( ^T * ) = Pn ( ^T * ) aw •

Применение уравнения (14) требует конкретизации зависимости активности воды от концентрации растворенного в ней вещества. В настоящее время из литературы известно несколько вариантов таких соотношений. Для неорганических солей широкое распространение получили уравнения, основанные на аппроксимации результатов экспериментальных измерений для заданного вещества с помощью полиномиальных функций [18–20]. В данной работе используется кубическое уравнение относительно массовой доли растворимого вещества в частице Y , построенное на основе измерений активности воды для частиц хлорида натрия [18]:

a, = 1 - 5,5741 x 10 - 3 Y - 5,8805 x 10 ^{- 5} Y ² - 3,2005 x 10 ^{- 6} Y ³ . (15)

Это соотношение, согласно работе [11], показывает лучшую, по сравнению с другими уравнениями, точность аппроксимации экспериментальных данных для активности воды.

Отличие предлагаемой в данной работе модели от описанных в работах [9–11] заключается в дополнительном учете изменения концентрации раствора за счет растворения кристаллического ядра в виде:

n. - n, )p₉ v

Y = 100 • -— ^{( 2   2 k} )    ² ----,

⁽ n 2 ^- n 2 _k ^)p 2 v 2 + n 1 ^p 1 ^v 1

где pj и p2 — плотности воды и растворяемого вещества соответственно. Таким образом, выражение для активности воды становится функцией двух переменных: a^ (n, n2к).

В результате уравнение для изменения количества молекул воды в частице принимает вид:

dn   ^{4 п} r * D f^Pn ^{( т} „ ^)Гф a_w ^{( n} 1 , n 2 k )     Г LM ^Г 1   1 ^X 2 c у

1 =exp     1+ dt          kb       (T„       T*         L Rg I TO  T* J  r*kbT*.

где радиус частицы определяется из соотношения (11).

Для замыкания уравнения (17) требуется записать соотношения для температуры T и количества кристаллического вещества частицы n . В предположении, что процесс растворения кристаллического вещества является диффузионным и зависит от концентрации раствора на поверхности частицы, уравнение для скорости растворения кристаллического вещества будет иметь вид:

= ⁶ ( « 1 - лА-⁴^^ [ ( C n - C j6( C « - C J + ( C pn - C i ) 0 ( C i - C pn ) ]} ,         (18)

dt                      I              Ml 2                                                                      I где

f 3v2 («2k + Of’ = k [     4n

_{c =} M 2      ( « 2 - « 2 k )

'   ^N a ( « 1 v 1 ⁺ ( « 2 - « 2 k ) v 2 )

Здесь: C_n , C_pn , C_t — массовая концентрация насыщенного, перенасыщенного и текущего растворов на поверхности нерастворенного ядра частицы; N_a — число Авогадро; D_d — коэффициент диффузии растворенных молекул в растворе; 0 ( x ) — функция Хевисайда, которая позволяет «выключать» растворение ядра до тех пор, пока не сформируется адсорбционных слой необходимой емкости ( « = A ), а также «запускать» процесс растворения при C . <  C_n и процесс кристаллизации при C . >  C_pп .

Поскольку конденсация сопровождается выделением тепла, а испарение — его поглощением, то температура частицы T (предполагается, что частица нагрета равномерно) изменяется. В свою очередь, за счет теплопроводности происходит теплообмен частицы с окружающим воздухом, в ходе которого температура частицы стремится уравняться с температурой окружающей среды T , полагающейся постоянной. В результате скорость изменения температуры частицы определяется соотношением:

cm — = 4 nrX(T„ -T) + L dm, p dt           v ' dt

где c_p — удельная теплоемкость частицы, и — коэффициент теплопроводности влажного воздуха, L — удельная теплота парообразования/конденсации. Учитывая, что масса частицы равна m = « р, v + n ₂р₂ v ₂, а количество молекул растворяемого вещества постоянно «₂ = const, уравнение (19) перепишем в виде:

dT * dt

c p ( « 1 Р 1 v 1 ⁺ « 2 Р 2 ^V 2 ) [

dn

4nr.x ( T „^- T * ) + L Р 1 v 1 — .

Поскольку уравнения диффузии применимы к описанию процессов масштаба, существенно большего X — длины свободного пробега молекул воды в воздухе (в нормальных атмосферных условиях X = 10 ^{- 1} мкм), то для частиц радиусом около 1 мкм и менее (при этом число Кнудсена Kn = 10 ^{- 1}) диффузионное приближение нельзя считать достаточно строгим. Поэтому в уравнения конденсационного роста частиц и диффузии тепла вносятся поправки за счет изменения коэффициентов диффузии и теплопроводности [8]:

- 1

""I-1

D * = D_f

—1— +    , D f

1 + 5 c X/ r *    r * a c^ R g T * /(2 п M 1 )

---------------------------/--+--)                                                     '            .

^{1 +5} c ^{X r} *    ^r * ^a t P air C p ,_air ^/ R g T * /( ^{2 n M} air ) _]

В данной работе, как и в статье [9], приняты значения: массовый и температурный коэффициенты аккомодации a_c = 1 и a_t = 0,3 ; 5_C =5^ = 2/3 ; p_air , c_{p aH} — плотность и удельная теплоемкость влажного воздуха.

3.    Модель гигроскопического изменения размера частицы хлорида натрия

Уравнения (17), (18) и (20) относительно переменных « , «_2к и T совместно с начальными условиями (4)-(9) позволяют описать эволюцию размера и температуры частицы при ее растворении и превращении в каплю, увлажнении и испарении капли, а также при ее кристаллизации. Система уравнений решалась последовательно с использованием численного метода Эйлера. Следует отметить, что данный численный метод чувствителен к величине шага по времени, поэтому в расчетах проводилось его дробление до достижения сходящегося решения.

Введенные в модель обозначения и использованные при расчетах значения параметров взяты из статьи [11] и представлены в таблице 1.

Таблица 1. Расчетные данные

Параметр	Обозначение	Размерность	Значение/уравнение
Молярная масса NaCl	M	кг/моль	58,45 х 10 - 3
Плотность NaCl	Р 2	кг/м3	2165
Объем NaCl	v 2	м 3	М /(Рг N ) = 4,487 х 10 - 29
Диаметр молекулы воды	d	м	« 3 х 10 - 10
Молярная масса воды	M 1	кг/моль	18 х 10 - 3
Плотность воды	Р 1	кг/м3	993,36
Объем молекулы воды	v 1	м 3	М 1 /( Р 1 N a ) = 3,012 х 10 - 29
Поверхностное натяжение воды	^ 1	Н/м	73 х 10 " 3
Удельная теплоемкость NaCl	cp	Дж/(К • кг)	в расчете предполагалась равной удельной теплоемкости воды, то есть 4179
Массовая  концентрация  насыщенного  и перенасыщенного раствора NaCl в воде	Cn , C pn	кг/м3	306,914, 460,371
Равновесное давление насыщенного пара при заданной температуре	Р п ( Т )	Па	2,3388 х 103для Т = 293 К; 3,3629 х 103 для Т = 299,15 К; 9,5898 х 103 для Т = 318 К
Коэффициент диффузии пара	D f	м2/с	22 х 10 - 6
Коэффициент диффузии NaClа в растворе	D d	м2/с	3 х 10 - 10
Плотность воздуха при 22°С	P air	кг/м3	1,18
Удельная теплоемкость воздуха при 22°С	c p ,air	Дж/(Юкг)	1005
Коэффициент теплопроводности сухого воздуха	a	Дж/(Юсм)	( 7,3172 х 10 - 5 ) Т с + 4,1147 х 10 - 3
Коэффициент теплопроводности насыщенного пара	v	Дж/(Юсм)	( 1,663 х 10 - 7 ) Т 2 - ( 3,528 х 10 - 5 ) Т с + 1,484 х 10"2
Коэффициент теплопроводности влажного воздуха	И	Дж/(Юсм)	( ха + Xv ( 0,8536 xv - ха ))/( 1 - 0,1464 xv ) , где x v = 0,0185
Удельная теплота парообразования/конденсации	L	Дж/кг	10 3 ( 2500,8 - 2,36 ( Т с - 273,15 ) + + 0,0016 ( Т с - 273,15 ) 2 - 0,00006 ( Т с - 273,15 ) 3 j

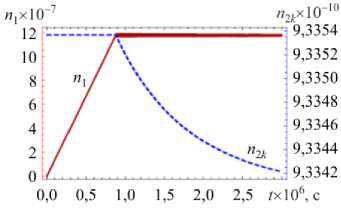
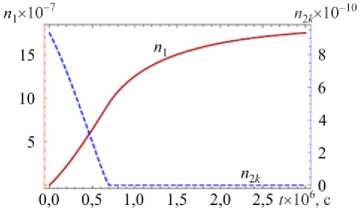
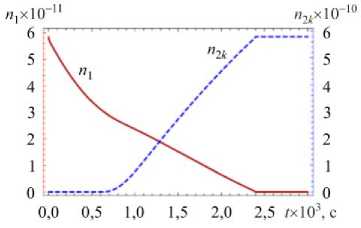
На рисунке 3 показаны вычисленные на основе модели временные зависимости количества в частице молекул воды n и нерастворенных молекул хлорида натрия n при значениях относительной влажности окружающего воздуха ф = 0,35 (ниже точки кристаллизации ERH) и ф = 0,9 (выше точки растворения DRH) при T = 293 К. Исследование проводилось как для частицы, находящейся в начальный момент времени в сухом состоянии ( п₁₀ = 0) и имеющей радиус r₀ = 1 мкм (что соответствует общему количеству растворяемого вещества в частице п = 9,3 х 10 ¹⁰), а также для частицы, которая в начальный момент была полностью растворена ( n ₀ = 0,91 п ), а ее радиус составлял r₀ = 1,69 мкм (что отвечает n₂ = 9,3 х 10 ¹⁰).

Из рисунка 3 а видно, что для частицы, находящейся в исходный момент в сухом состоянии, сначала происходит формирование адсорбционного слоя без растворения ядра. Когда емкость слоя становится критической для данной относительной влажности, частица начинает растворяться, однако вследствие низкой влажности окружающего воздуха приток молекул воды в частицу не осуществляется, и это приводит к приостановлению процесса растворения. При помещении сухой частицы в воздух с высокой относительной влажностью (Рис. 3 в ) на начальном этапе, при t <  1 х 10 ^{- 6} с, также наблюдается адсорбция, за которой следует полное растворение хлорида натрия и постепенное увеличение количества молекул воды в капле вплоть до достижения равновесного состояния.

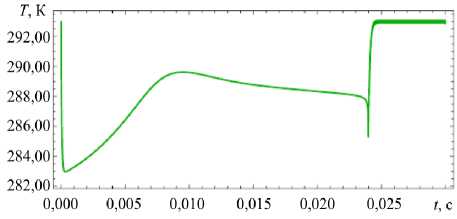
При попадании полностью растворенной частицы в воздух с низкой относительной влажностью (Рис. 3 д ) на первом этапе молекулы воды интенсивно испаряются с поверхности капли, что вызывает повышение концентрации раствора внутри капли. Когда раствор становится перенасыщенным, наряду с испарением частицы начинается ее кристаллизация, которая продолжается до установившегося состояния. Поведение растворенной частицы в воздухе с относительной влажностью выше DRH соответствует процессу конденсации капли (Рис. 3 ж ).

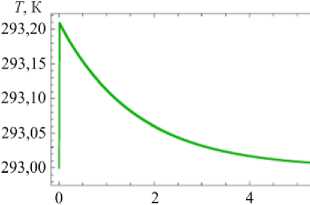
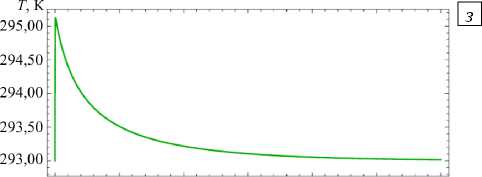
Как следует из рисунка 3б, г, з, с ростом размера (за счет конденсации молекул воды) частица нагревается, при этом максимальное увеличение температуры происходит при условии, когда концентрация раствора соли на поверхности частицы минимальна и, как следствие, конденсация воды наиболее интенсивна. По мере снижения концентрации нагревание частицы за счет конденсации уменьшается и преобладающим становится процесс теплопроводности, способствующий отводу тепла от частицы.

При интенсивном испарении влаги с поверхности частицы ее температура в начальный момент резко падает (Рис. 3 е ). По мере снижения концентрации воды в капле начинает превалировать процесс теплопроводности, приводящий к постепенному нагреву капли. Однако, когда концентрация раствора достигает значения перенасыщения и начинается кристаллизация, температура частицы снова уменьшается, поскольку часть соли из раствора переходит в кристаллическое состояние, вследствие этого концентрация воды на поверхности частицы увеличивается. После завершения кристаллизации за счет теплопроводности температура частицы повышается до температуры окружающего ее воздуха.

Из рисунка 3 следует, что время установления равновесного состояния частицы меняется от микросекунд (Рис. 3 а ) до десятых долей секунд (Рис. 3 в , д , ж ) и зависит от того, насколько ее исходное состояние отличалось от равновесного.

а

295,50

295,00

294,50

294,00

293,50

293,00

в

0,00     0,05     0,10      0,15     0,20    0,25 г, с

д

е

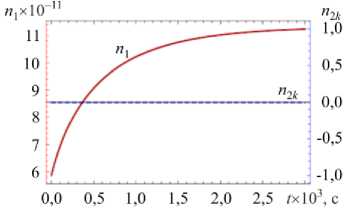
Рис. 3. Временные зависимости количества молекул воды

ж

0,00     0,05     0,10      0,15     0,20    0,25     ?, с n (сплошная линия), нерастворенных молекул хлорида натрия

п_2к (штриховая линия) в частице и температуры частицы для различных значений относительной влажности окружающего воздуха и начальной мольной доли воды в частице: ф = 0,35 , n ₁₀ = 0 ( а , б ); ф = 0,9, n ₁₀ = 0 ( в , г ); ф = 0,35 , n₀ = 0,91 n ( д , е ); ф = 0,9 , n ₀ = 0,91 n ( ж , з )

Чтобы определить корректность используемого в большинстве моделей, основанных на модификации уравнения Максвелла, перехода от уравнения (1) к (2), проводилась оценка изменения плотности частицы в процессе растворения. Расчеты осуществлялись для частицы диаметром 1 мкм, в начальный момент находящейся в сухом состоянии (n0 = 0), а затем помещенной во влажный воздух. Результаты моделирования для двух значений относительной влажности воздуха ϕ=0,8 и ϕ=0, 99 представлены в таблице 2 и на рисунке 4. В таблице приведены следующие значения: плотность в момент полного растворения кристаллического ядра (образования капли) — ρ ; минимальная плотность частицы — ρ , которая достигается в равновесном состоянии; ρ и ρ — соответственно, доли уменьшения плотности относительно начального и растворенного состояний.

Согласно полученным результатам происходит значительное изменение плотности частицы по сравнению с исходным значением ρ , не зависящее от относительной влажности воздуха. Если использовать соотношение (2) только для описания растворения капли (то есть в области справа от вертикальной штриховой линии на рисунке 4), то изменение плотности по отношению к плотности на начальной стадии растворения капли ρ будет варьироваться от 1,4% при относительной влажности воздуха близкой к гигроскопической точке до 11,6% при влажности 0,99.

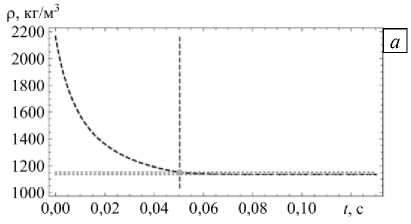
Рис. 4. Изменение плотности частицы радиуса r = 0, 5 мкм в процессе гигроскопического роста ее размера при T = 293 К, n = 0 , ρ=2165 кг/м3 и относительной влажности воздуха ϕ=0,8 (а) и ϕ=0,99 (б); вертикальная штриховая линия разделяет этапы растворения частицы, содержащей кристаллическое ядро, и роста размера капли без ядра

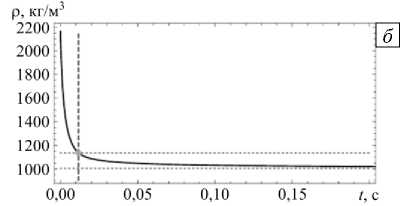
Таблица 2. Результаты моделирования изменения плотности частицы в процессе растворения

ϕ× 100, %	ρ , кг/м3	ρ    , кг/м3 min ,	ρ 0 - ρ min × 100, % ρ 0	ρ i - ρ min × 100, % ρ i
80	1152	1136	47,5	1,4
99	1136	1004	53,6	11,6

4.    Верификация модели

Верификация представленной в работе модели проводилась путем качественного и количественного сравнения ее предсказаний с экспериментальными данными об эволюции размера частиц хлорида натрия в режимах увлажнения и высушивания, а также с результатами измерений размера частиц в равновесном состоянии при увеличении и уменьшении относительной влажности воздуха (с изотермой абсорбции).

Тестирование модели в режиме увлажнения частицы осуществлялось на основе экспериментальных данных из работы [11], где разработана новая система измерения размера при росте капли, в которой предварительно очищенная и высушенная аэрозольная частица улавливается на покровное стекло микроскопа, помещенного в воздушную среду с контролируемой влажностью и температурой. Увеличение размера частицы фиксировалось видеокамерой. На рисунке 5 а показаны полученные описанным методом данные о росте частицы NaCl в воздухе с относительной влажностью ϕ= 0, 98 при T = 299,15 К. Следует отметить, что разработанный метод не позволяет измерять трехмерную структуру сухой частицы, и следовательно, начальный размер кристалла соли не известен. При моделировании начальный радиус частицы корректировался до тех пор, пока среднеквадратичная ошибка отклонения предсказаний модели от экспериментальных данных за 30-секундный испытательный период не сводилась к минимуму. Наилучшее совпадение предсказаний модели с экспериментальными данными получено для 2 r = 3, 85 мкм (см. Рис. 5 б ).

На рисунке 6 представлены результаты линейного регрессионного анализа экспериментальных и модельных значений диаметра как для всего интервала измерения размера частицы, так и только для области растворения кристаллического ядра. Как следует из графиков, наблюдается хорошая корреляция данных в обоих случаях (коэффициенты корреляции r и детерминации R ² близки к 1, уравнение линейной регрессии незначительно отклоняется от y = x ). Среднеквадратичная ошибка (Root Mean Square Error — RMSE), характеризующая отличие друг от друга прогнозируемых и экспериментальных значений, составляет ≈ 0,3 мкм. По сравнению с аналогичными данными,

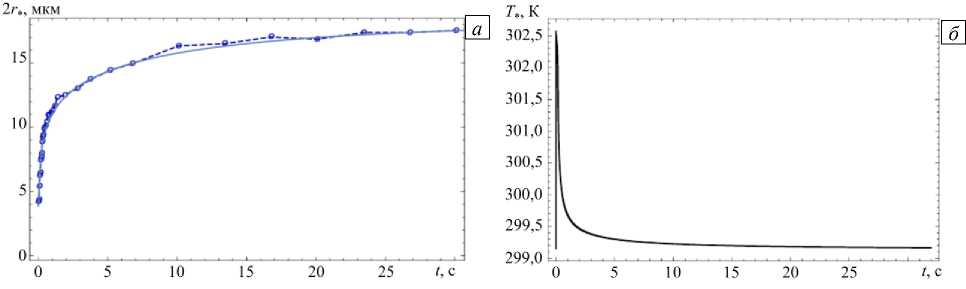
Рис. 5. Изменение во времени диаметра частицы, вычисленного с помощью предлагаемой модели (сплошная линия) и измеренного в эксперименте [11] (точки, соединенные штриховой линией) ( a ); температура частицы, предсказанная моделью, при ф = 0,98 , T = 299,15 К, 2 r ₀ = 3,85 мкм, п_{х 0}= 0 ( б )

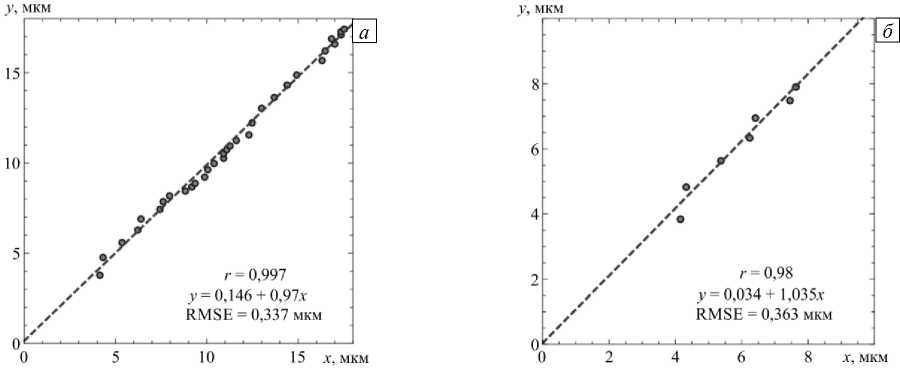
Рис. 6. Корреляция диаметров x, полученных в эксперименте, и диаметров y, предсказанных моделью, для всех моментов измерения (от 0 до 30 с) (a) и до момента растворения кристаллического ядра (б)

приведенными в работе [11], точность предсказания гигроскопического роста размера частицы предлагаемой в данной работе моделью увеличивается. Однако следует учитывать, что авторы статьи [11] использовали для исследования точности данные шести серий экспериментов, в то время как здесь расчет произведен по информации только об одном эксперименте.

Верификация модели в режиме испарения и кристаллизации проводилась на основе экспериментальных и модельных данных, представленных в статье [21]. В этой работе кинетика испарения капель NaCl изучалась с помощью прибора CK-EDB [22], позволяющего поместить сгенерированные и предварительно заряженные аэрозольные капли в центр электродинамического поля, создаваемого между двумя наборами концентрических цилиндрических электродов. Радиус изотропных капель в сухом воздухе определялся с помощью лазера. Однако этот метод не работает на стадии кристаллизации, когда нарушается изотропия частицы и резко меняется картина рассеяния. На рисунке 6 показан характер изменения размера частицы в режиме высушивания, полученный описанным выше методом. Эксперименты проводились при контролируемой температуре воздуха 293 К и 318 К для капель с различной начальной массовой долей соли (MFS — Mass Fraction of Solute). Для перехода к мольной доле воды использовалось соотношение:

% =

n ₁ n

MFS M

1 +

( 100 - MFS ) М_г

- 1

Результаты расчета радиуса частицы в процессах испарения и кристаллизации с помощью предлагаемой модели с параметрами, соответствующими условиям экспериментов, отображены на рисунке 7. Также представлены экспериментальные данные и прогнозы по модели из работы [21]. Из графиков следует, что существует достаточно хорошее совпадение результатов, полученных по модели автора, с экспериментальными данными в области испарения частицы, однако предлагаемая модель неверно предсказывает момент начала кристаллизации (вертикальная штриховая линия) при T = 318 К.

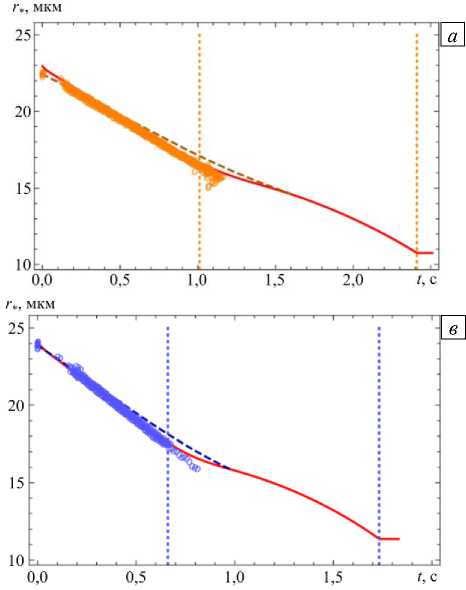
Рис. 7. Изменение радиуса капли NaCl в сухом воздухе ф = 0%

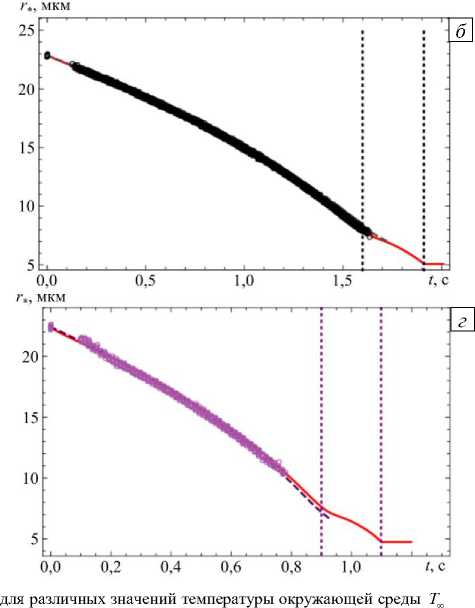
и начальных массовых долей хлорида натрия в капле MFS, полученные: в эксперименте (точки «○»); вычисленные по модели из [21] (штриховая линия) и по предлагаемой модели (сплошная линия): MFS = 20% , Т^ = 293 К, r = 22,95 мкм ( а );

MFS = 2,333%,  Тго = 293 К, r = 22,95 мкм (б);  MFS = 20,2%,  Тго = 318 К r = 24,14 мкм (в);  MFS = 2% , Т = 318 К, r = 22,55 мкм (г); вертикальные линии соответствуют времени начала и конца кристаллизации

Таблица 3. Оценки точности расчета гигроскопического уменьшения размера частицы хлорида натрия

Условия эксперимента	RMSE, мкм	Уравнение регрессии	R 2	r = Л?
Предсказания модели из [21 ]
MFS = 20%, Т = 293 К	0,452	у = 2,85 + 0,868 x	0,997	0,998
MFS = 2,333%, Т„ = 293 К	0,279	у = 0,665 + 0,973 x	0,999	0,999
MFS = 20,2%, Т„ = 318 К	0,509	у = 3,195 + 0,862 x	0,995	0,997
MFS = 2% , Т. = 318 К	0,289	у = 0,327 + 0,995 x	0,997	0,998
Предсказания предлагаемой модели
MFS = 20%, Т = 293 К	0,198	у = 0,088 + 1,004 x	0,996	0,998
MFS = 2,333%, Т„ = 293 К	0,138	у = - 0,238 + 1,009 x	0,999	0,999
MFS = 20,2%, Т„ = 318 К	0,154	у = 0,757 + 0,961 x	0,992	0,996
MFS = 2% , Т„ = 318 К	0,170	у = 0,458 + 0,976 x	0,998	0,999

Количественные оценки погрешности приведены в таблице 3. Для удобства сравнения аналогичные данные получены и по модели из статьи [21]. Как следует из таблицы, при расчете по предлагаемой модели уменьшаются среднеквадратичные отклонения (RMSE) экспериментальных и модельных данных при всех рассмотренных режимах испытаний, а кривая линейной регрессии заметно приближается к прямой у = x .

На рисунке 8 приведены изотермы абсорбции для аэрозольных частиц хлорида натрия, предсказываемые предлагаемой в данной работе моделью (сплошные линии c « ▲ » и « ▼ »), и экспериментальные данные, взятые из работы [23] (« х » и «о»). Сплошная линия c « ▲ » и маркеры «о» соответствуют частице, которая для каждого задаваемого значения ф находится в начальный момент времени в сухом состоянии, что тождественно режиму постепенного увеличения относительной влажности воздуха. Линия с символами « ▼ » и точки-маркеры « х » получены для изначально растворенной частицы, то есть соответствуют режиму уменьшения относительной влажности. Как следует из рисунка, предлагаемая в работе модель описывает наблюдаемый в экспериментах гистерезис гигроскопических свойств частиц хлорида натрия, а также предсказывает влажности фазовых переходов растворения

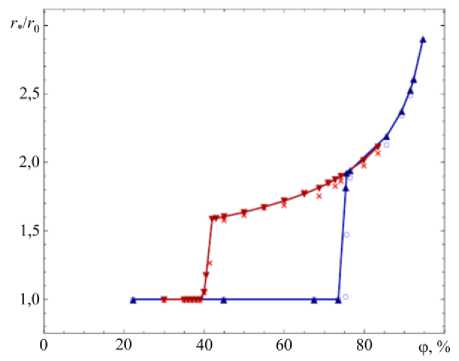
и кристаллизации. Следует отметить, что согласно данной модели в режиме возрастания относительной влажности воздуха (при ф< DRH) частица находится в квазистационарном состоянии, которое проявляется в циклической смене процессов конденсации влаги и ее испарения на поверхности частицы, при этом содержание молекул воды в частице колеблется вокруг среднего значения. Такое поведение связано в основном с тем, что активность воды зависит не только от количества ее молекул в частице, но и от количества растворенного вещества (хлорида натрия). Фазовый переход в режиме испарения напрямую определяется значением концентрации перенасыщения C , при превышении которого вследствие испарения Рис. 8. Изотерма абсорбции для NaCl воды с поверхности частицы начинается кристаллизация.

Количественная оценка погрешности расчетов приведена в таблице 4. Основная причина снижения точности предсказания характера изотермы абсорбции связана с небольшим опережением момента начала перехода к фазе растворения.

Таблица 4. Оценки точности расчета изотермы абсорбции для частицы хлорида натрия

Режим эксперимента	RMSE, мкм	Уравнение регрессии	R 2	r = Цё
Увеличение ф	0,279	у = 0,294 + 0,902 x	0,854	0,924
Снижение ф	0,055	у =- 0,028 + 1,04 x	0,983	0,991

5. Выводы

Предложена и построена математическая модель, позволяющая описывать кинетику взаимодействия водорастворимой однородной и химически нейтральной аэрозольной частицы с влажным воздухом на всех этапах гигроскопического роста/уменьшения ее размера. Благодаря учету зависимости активности воды от концентрации растворенной части частицы и введению дополнительного уравнения для эволюции нерастворенного ядра, в отличие от работы [11], удалось избежать искусственного разделения этапов растворения частицы с нерастворенным ядром и без него.

На основе предложенной модели рассмотрены различные сценарии изменения состояния частицы в зависимости от ее начальной степени растворения и относительной влажности окружающей среды. Показано, что предсказания предложенной модели качественно и количественно согласуются с экспериментальными данными об эволюции размера частиц хлорида натрия в режимах увлажнения и высушивания, а также с результатами измерений размеров частиц в равновесном состоянии при увеличении и уменьшении относительной влажности воздуха.

Проведена оценка изменения плотности частицы, находящейся в начальный момент в сухом состоянии. Установлено, что при гигроскопическом росте частицы в воздухе с высокой относительной влажностью (0,99) изменение плотности превышает 10%, что необходимо принимать во внимание при переходе от уравнения (1) к (2) в моделях, базирующихся на модификации уравнения Максвелла.

Разработанная модель может быть полезной для создания комплексной математической модели коагуляции и оседания частиц пылевых аэрозолей с учетом гигроскопического роста/уменьшения размера аэрозольных частиц.

Исследование выполнено при поддержке РФФИ (проект № 20-45-596020) и в рамках задания Министерства науки и высшего образования Российской Федерации (тема № 121031700169-1).