Эволюционная модель плоского пластического течения материала с учетом сил инерции

1. Математическая модель

Рассмотрим плоскую задачу об установившемся пластическом течении материала вне выпуклого отверстия, границу L которого можно представить в параметрическом виде [1]:

x_L = F ' ( в ) cose + F ( в ) sine,    y_L = F ' ( в ) sine - F ( в ) cose.

Здесь x_L , y_L — декартовы координаты точки, лежащей на кривой L ; F ( в ) — 2п -периодическая опорная функция кривой L ; в е [ 0,2п ) — угол между касательной к кривой L и осью Ox . Радиус кривизны границы L определяется функцией р ( в ) = F "( в ) + F ( в ) ; предполагается, что р ( в ) >0. Единичные векторы, направленные по касательной и по нормали к точкам линии L , имеют вид t = (cosβ, sin β) и n = (sinβ, - cosв) соответственно.

Следуя [1], для описания течения материала воспользуемся криволинейной системой координат (α, β) , индуцированной кривой L с опорной функцией F ( в ) :

x ( а, в ) = F ' ( в ) cosв + ( F ( в ) + а ) sin в , У ( а, в ) = F ' ( в ) sin в - ( F ( в ) + а ) cosв,             (1)

откуда якобиан преобразования D ( x,y )/ D ( а,в ) = р + а>0. Координатные линии H = const > 0 представляют собой эквидистантные кривые с опорной функцией F ( в ) + а, а координатные линии β = const образуют семейство прямых, ортогональных L .

Проекции вектора скорости перемещений на оси криволинейной системы координат обозначим через U и V . Связь между компонентами вектора скорости в декартовых и криволинейных координатах

зададим соотношением ( u , v ) = U n + V t . Тогда компоненты тензора скоростей деформаций в криволинейных координатах (1) запишутся как

= dU

^е аа     д а ’ ^е ав

1 (д V    1 (д U

I ^+1

2 (д а р + а (д р

V

= 1 ( d V р + а (д р

Плоская задача пластичности с учетом сил инерции, обуславливаемых только конвективным переносом, сводится в криволинейных координатах к системе пяти уравнений для напряжений

(°_аа,°_а в ’^о вв ) и поля скоростей (U , V ) пластической среды [2, 3]:

+^ +    '• = Y (и ™ + V  (U - V]],

д а р + а д р р + а      ( д а р + а (д р     JJ

+    ^Ои+20$.=Y (и dV+V (dv+и 11,

д а р + а д р р + а ( д а р + а (д р J J

^£ аа ⁺ £ вв = ⁰,          ° ^вв = ^£ ° ^{П £вв} , ( °™ ^{- д} вв ) ^{2 + 40} ■ = ^{4 k 2} .

σ αβ           ε αβ

Первые два уравнения системы (2) являются уравнениями движения сплошной среды; третье уравнение выражает условие несжимаемости; четвертое — условие совпадения главных осей тензора напряжений и тензора скоростей деформаций; замыкающее, пятое, уравнение выражает условие пластичности. Положительные постоянные у и к есть плотность и предел текучести.

Воспользуемся подстановкой Леви оаа=о — к sin29,    °ав = к cos29,    овв=о + к sin29

и перейдем к безразмерным переменным ( U , V ) = v , ( U ', V ' ), о = 2 к о ' , где v , — характерный масштаб скорости. В результате уравнения (2) принимают вид (штрихи опущены; e = ( 2 к ) ¹ р v ,² — безразмерный параметр):

д о д а

^д 9

cos 29--

д а

sin29 (д 9 ,)   ( д U V (д U

I +1 I = e I U+I

р + а (д р    J ( д а р + а (д р

V

1 д о р + а д р

. _д 9 cos29 ( д 9 .1    ( д V V (д V

- sin 29— +----I — +1 I = e I U — +---I — + U

д а  р + а (д р

д а р + а (д р

,

dU 1 ( d V _TT --+---I — + U д а р + а (д р

= 0,

д V 1 (д U „1 2ctg29 (д V 1 л — +---I--V I---—I — + U 1 = 0. да р + а (др ) р + а (др )

Модель плоского стационарного пластического течения материала хорошо изучена в случае e = 0 , когда в уравнениях равновесия не учитывается эффект инерции. При этом система уравнений (4) распадается на две подсистемы. Из первой подсистемы определяются напряжения, из второй (с использованием найденных напряжений) — поле скоростей. В рассматриваемом случае e * 0, что приводит к необходимости решать полную систему из четырех уравнений. Интересно отметить, что в обоих случая (e = 0 и e * 0 ) система уравнений (4) имеет два семейства вещественных характеристик, задаваемых уравнениями dβ               ctgθ         tgθ

Л- 1,2 ; Л- 1                   , Л 2                .

d а             р + а р + а

Далее будет показано, что при e * 0 каждой кратной характеристике (5) соответствует лишь один собственный вектор и при 9 = п п /2 скорости характеристик становятся бесконечными. В силу этого система уравнений (4) не является гиперболической, что представляет дополнительные трудности при ее исследовании.

• 2.    Аналог характеристической формы уравнений пластического течения

Система уравнений пластического течения (4) представима в виде

AU a + BU = G 1 ,

где U = ( U , V , 9, о ) T — вектор-столбец искомых величин, A u B — матрицы, коэффициенты которых зависят от искомого вектора U , вектор G ₁ — правая часть. Определители матриц A и B равны sin 2θ и ( р + a )^{- 4} sin 29 соответственно. Вырождение матриц и обращение скоростей характеристик в бесконечность происходит при θ=π n 2 ( n — целое число). Умножение векторного уравнения (6) на матрицу A -1 (при 9 * п п /2) приводит систему (4) к эволюционному виду

U + MU e = G                                 (7)

с матрицей M = M '/ ( p + a ) (координата a играет роль времени),

f         0                             1 0 0    1 M' = 1                  -2ctg29 0 0 - eU /sin29     e (V + 2U ctg29)/sin29 -ctg29 -1/sin20 - e (V + U ctg29) e (U + V ctg29 + 2U ctg2 29) -1/sin20 -ctg29 у и правой частью G = G'/(р + a),

'                        -U                       '

V + 2 U ctg29 ctg29 - 2 eU ( V + U ctg29)/sin 29 ^ sin 29 - e ( U ² + V ² ) + ( cos 29 - 2 eU ( V + U ctg29 ) ) ctg29 _у

Невырожденная матрица M имеет кратные вещественные собственные значения λ₁ и λ₂ , задаваемые формулой (5). Каждому собственному значению соответствует лишь один правый собственный вектор-столбец h 1 = ( 0, 0,1,1 ) T и h ₂ = ( 0, 0, - 1,1 ) T . Вычислим правые присоединенные собственные векторы р i , удовлетворяющие уравнениям Mp , = \р , + h _i , и составим матрицу перехода R , в которой первый и третий столбцы — собственные векторы, второй и четвертый — присоединенные собственные векторы:

f ⁰

R = ⁰

- 2 (p + a) sin29/( e (V + U ctg9))

(p + a) sin20/( e (V + U ctg9))

- 2 ( p + a ) cos 2 9/ ( e ( V - U tg9 ))' - ( p + a ) sin 20/ ( e ( V - U tg9 ) )

( 1                     0                      1

Подставим в (7) выражение U = RV и умножим слева на матрицу R ¹. В результате этих преобразований система уравнений (7) принимает вид

V a + JV = K ,

f

1 Где V = ^{R -1} U =2

о + 9               ^

- e ( V + U ctg9 )( U - V ctg9 )/( p + a ) о - 9

- e ( V - U tg9 )( U + V tg9 )/( p + a ) _у

—новый искомый вектор, J = R 1 MR =

X *	1	0	0 1
0	λ 1	0	0
0	0	λ 2	1
ч 0	0	0	^ 2 у

Жорданова форма матрицы M , K = R ¹ ( G - R _a V - MR _e V ) — вектор, конкретное выражение которого здесь не приводится из-за его громоздкости.

Уравнения пластического течения (8) представляют аналог характеристической формы системы (4), но, в отличие от классических гиперболических систем [4], имеют недиагональную матрицу J. Несмотря на это, можно показать, что задача Коши для уравнения (8) с заданными при а = 0 гладкими «начальными» данными, для которых собственные значения (5) ограничены, локально разрешима, то есть ее непрерывное решение существует и единственно при достаточно малых и положительных значениях а . В дальнейшем ограничимся численным моделированием и исследованием только таких непрерывных решений.

• 3.    Разностная схема

Для численного решения задачи Коши, описывающей при а > 0 пластическое течение материала на основе эволюционной системы уравнений (7) с начальными условиями U ( 0, в ) = U ₀ ( в ) , будем использовать следующую разностную схему:

n

j +1/2

U

• n +1

j +1/2

—

U

n

j +1/2

n

V j +1

—

V j ⁿ

^T n

h

j +1/2

= 0,

r j ⁿ

Vj* ⁺¹

—

^Vj ⁿ

+

U^{n +1}

U j +1/2

—

U

• n +1

j —1/2

^T n

h

+ a.

n

^V j +1

—

V n —

2 h

= g 2 ,

n rj+1/2

O'

. n +1

j +1/2

—

O'

n

j +1/2

n

CT

. n +1

1 - j

^T n

—

CT

n

+ a.

^T n

⁺ a 31

U^{n +1}

^C j +3/2

—

U

• n +1

j —1/2

U

• n + 1

j +1/2

—

2 h

+ a.

F ^{n +1}

V j +1

—

V" ⁺¹

h

+ a

O'

n

j +3/2

—

O'

n

j —1/2

2 h

+ a.

' 34

n

^CT j +1

—

h

n

CT i

= g 3 ,

U^{n +1}

^U j —1/2

h

+ a,

iz ^{n +1}

^V j +1

—

F ⁿ +1 j —1

2 h

+ a,

O

. n +1

j +1/2

—

O

h

. n +1

j —1/2

+ a.

CT

n

j +1

—

CT

n

j —1

2 h

= g 4 ,

где r = p + а, а коэффициенты aj и gi будут представлены ниже.

При записи схемы (9) использованы следующие сокращенные обозначения для сеточных функций: n —1

Л = f (а n ,e j ), f j +1/2 = f ( а n ,P j +1/2 ) , P j = jh , P j +1/2 = ( j + V² ) h , а n = £ т _m , где h ^— постоянный шаг m =0

разностной сетки по переменной в е [ 0,2п ] , а т n — переменный шаг по эволюционной переменной а, выбираемый из условия устойчивости Куранта

τ _n = zh

max [ max ( | X , | n , | X 2 | n ) ] , (10)

характерного для гиперболических систем [4]. В формуле (10) величины | Х 1 1 n и | X₂ | n — сеточные значения модулей скоростей характеристик (5); z < 1 — коэффициент запаса устойчивости (в приводимых ниже расчетах принимается z = 0,5). Разностные граничные условия задаются исходя из требования 2п -периодичности функций по переменной P .

Опишем явную реализацию схемы (9). Сначала из ее первого уравнения найдем значения U " j^ , которыми воспользуемся во втором уравнении для вычисления V j ⁺¹. Затем U n ++ 1 _/2 и V j ⁺¹ применим для определения 0 n +1 _/2 из третьего уравнения схемы (9), а затем с помощью U ” j ₂, V j ⁺¹ и 0 n +1 _/2 найдем ст ⁿ n ⁺¹ из ее четвертого уравнения. После этого рассчитаем элементы aik матрицы M ' и компоненты gk вектора G ', входящие в схему (9); значения a ₂₂ и g ₂ во втором уравнении вычислим по известным величинам U n ++Ш , V j и 0 n _{+ 1/2}; значения a ₃ k и g ₃ в третьем уравнении определим через U " ++j ₂ , V j ⁺¹ и 0 n _{+ 1/2}; значения a ₄ k и g ₄ в четвертом уравнении найдем по величинам U n ^ , V j ⁺¹ и 0 n +1 _/2.

Построенная таким образом разностная схема (9) имеет второй порядок аппроксимации по переменной P и первый — по эволюционной переменной а. Схема допускает явную реализацию и в линейном приближении является устойчивой при выполнении условия Куранта (10). Она представляет собой отдаленный аналог схемы «крест» для уравнений газовой динамики [4] и подобна разностной схеме, которая эффективно использована для численного моделирования в рамках уравнений мелкой воды волновых течений жидкости, вызванных полным или частичным разрушением плотины гидросооружения [5], сходом в воду берегового оползня [6], а также поднятием в результате землетрясения прибрежного участка дна, приводящим к возникновению волны цунами [7]. Разностную схему (9) также можно рассматривать как обобщение численных алгоритмов, которые применялись в работах [8, 9] для моделирования пластических течений материалов без учета влияния сил инерции.

• 4.    Результаты численных расчетов

Система уравнений (4) при р = р₀ = const имеет следующее, не зависящее от переменной в решение

U = C 1 /(р₀ + а ) , V = 0, 6 = п/4, o = ln ( р₀ + а ) + eU ² /2 + C 2 ,                  (11)

в котором C ₁ и C ₂ — произвольные постоянные. Решение описывает инерционное пластическое течение материала вне круглого отверстия радиуса ρ₀ . На этом точном решении проведем тестирование предложенного в предыдущем разделе численного алгоритма. Для этого при α=0 зададим численные начальные данные, соответствующие решению (11) с р₀ = 1, C 1 = 0,2 и C ₂ = 0,3, и исследуем сходимость получаемого по схеме (9) разностного решения U _h ( а, в j ) к точному решению U ( а ) при некотором фиксированном а = а * >0. Если а _п < а * <а _{п + 1}, то для построения разностного решения U _h ( а * , в j ) последний, п- й, шаг схемы по эволюционной переменной выбирается по формуле т П = а * - а _п < т _п .

Положим, что при h ^ 0 разностное решение U _h ( а * , в j ) сходится к точному решению U ( а * ) с порядком 5 в норме С , если

A U h = |U h ( а * ,₽ j ) - U ( а *)| = Ch .

Здесь ||f ( P j )|| = maxI^f ( в j ) , l^f ( j — модуль вектора f ( в j ) . C — величина, не зависящая от h . Для приближенного определения порядка сходимости s проведем расчет на двух сетках (с шагами h и h 2 ), после чего применим формулу Рунге

5 = l0g 2 ( A U h /A U h /2 ) .

При а * =5 и h = 2п/100 из соотношений (12) и (13) получим: A U _h =5,685 - 10 ², A U _h /2 =2,914 - 10 ², 5 = 0,964 ® 1. Таким образом, разностное решение сходится к точному решению с первым порядком, что связано с первым порядком аппроксимации по эволюционной переменной α. Приведем ошибку разностного решения в норме С по каждой компоненте вектора искомых величин: A U_h =0,097 - 10^-2, A o _h =5,684 - 10^-2, A U_h /2 =0,050 - 10^-2, A o _{h /2} =2,914 - 10 ^{- 2} . Постоянные компоненты V и 6 решения (11) вычисляются точно ( A V_h = A 6 _h = 0), поэтому ошибка разностного решения связана с погрешностями, возникающими при вычислении компонент U и σ .

Выполним те же расчеты, но в формуле (10) заменим h на h ² , что обеспечивает второй порядок аппроксимации как по переменной α , так и по пременной β . В этом случае точность разностного решения существенно возрастает: A U_h =0,040 - 10^-3, A o _h =2,991 - 10 -3 , A U_{h /2} =0,016 - 10^-3, A o _{h /2} =0,821 - 10 - 3 , и порядок сходимости становится вторым A U _h =2,991 - 10 -3 , A U _{h /2} =0,821 - 10^-3, 5 = 1,865 ® 2.

Следующие численные расчеты иллюстрируют влияние эффекта инерции при пластическом течении материала. Пусть при α=0 на круглом отверстии ( ρ=1) заданы значения скоростей и параметризации напряжений (Рис. 1):

V = - 0,1 sin в, 0 = n/4 - 0,2cosв.

U = и cos в, o = 0,25 + 0,2sinв,

Здесь и — параметр , отвечающий за амплитуду скоростей на отверстии.

Безразмерные напряжения σ_αα , σ_αβ и σ_ββ вычислим по формулам (3) при k =1 2. Для оценки влияния инерционных эффектов проведем численное интегрирование уравнений (7) с условиями (14) на основе схемы (9) при e =0 (классическая модель пластического течения) и различных значениях e >0 (модель, учитывающая влияние инерции). Расчет проведем с шагом h = п/100 до а * =5; параметр и выберем равным 0,35 и 0,5 . Предположим, что отверстие является круглым (кривизна ρ=1).

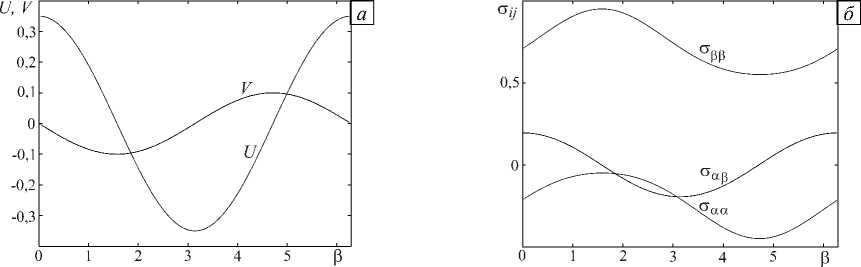
Рис. 1. Поле скоростей ( а ) и напряжений ( б ) при а = 0, х = 0,35

Результаты сравнения в норме С численных решений уравнений (7) при e = 0 и e + 0 приведены в таблице. Значения А о_рр не приводятся, поскольку они совпадают со значениями А о_аа в силу подстановки Леви (3).

Таблица. Максимальное отличие между решениями уравнений (7) при e = 0 и e ^ 0 для различных значений х

e	A U		А V		А о αα		А ОаР
	х = 0,35	х = 0,5	х = 0,35	х = 0,5	х = 0,35	х = 0,5	х = 0,35	х = 0,5
0,5	0,0026	0,0137	0,0106	0,0534	0,0369	0,1111	0,0101	0,0407
1,0	0,0055	0,0335	0,0227	0,1222	0,0761	0,2564	0,0217	0,0902
1,5	0,0090	0,0608	0,0367	0,2103	0,1181	0,4454	0,0351	0,1498
2,0	0,0131	0,0940	0,0521	0,3190	0,1668	0,6897	0,0467	0,2086

Качественный характер решения, полученного при e + 0 и e = 0 , совпадает (см. Рис. 2), но с ростом параметров х и e количественные различия усиливаются. Как видно из таблицы, с увеличением параметра инерции e и/или «начальной» амплитуды скорости х наблюдается пропорциональный рост расхождения решений, полученных по классической ( e = 0) и модифицированной ( e + 0 ) моделям. Таким образом, использование модели пластического течения с учетом эффекта инерции необходимо в случаях достаточно больших значений амплитуд скоростей в окрестности отверстия и значений параметра инерции (материал с высокой плотностью и низким пределом текучести).

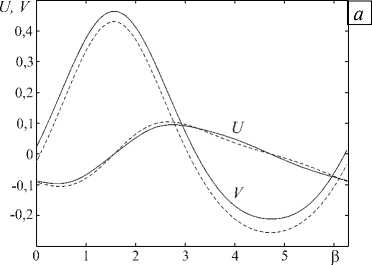
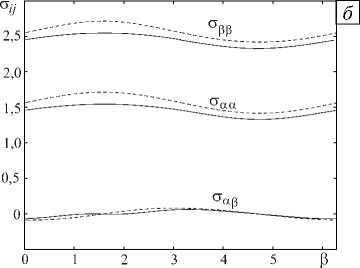
Рис. 2. Поле скоростей ( а ) и напряжений ( б ) в пластическом течении вне круга при а = 5, х = 0,35 ; сплошные линии соответствуют e =2 , пунктирные – e =0

Проведем аналогичный расчет распространения пластического состояния от границы эллипса с полуосями a и b , что соответствует следующему выбору опорной функции: F ( в ) = a²^ sin² в + b ² cos² р. При этом входящий в расчетные формулы (9) радиус кривизны границы L имеет вид : р ( р ) = 2V2 a² b ²/ ( a ² + b ² + ( b ² - a ²) cos ( 2p ) ) .

Выполненные численные эксперименты свидетельствуют, что отклонение формы выпуклого отверстия от круга (при одних и тех же граничных условиях для скоростей и напряжений) может привести как к усилению, так и к ослаблению влияния эффекта инерции. На рисунке 3 показаны результаты расчета, соответствующие пластическому течению вне эллипса с полуосями a = 1,5 и b = 0,5 при заданных граничных условиях (14) с х = 0,35. Как и в предыдущем примере, использовался шаг h = п/100, и расчет проводился до значения α^* =5. Сравнение графиков на рисунках 2 и 3 позволяет сделать вывод, что изменение формы отверстия оказывает заметное влияние на основные параметры пластического течения.

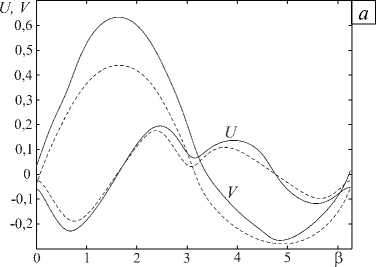
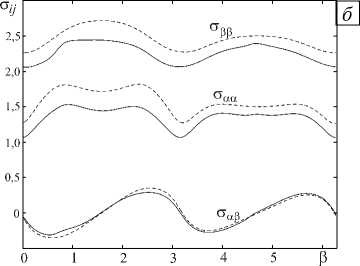
Рис. 3. Поле скоростей ( а ) и напряжений ( б ) при а = 5, и = 0,35 в пластическом течении вне эллипса; сплошные линии соответствуют e =2 , пунктирные – e =0

• 5.    Заключение

Предложена эволюционная нелинейная модель плоского стационарного пластического течения материала вне выпуклого отверстия с учетом эффекта инерции (4). Модель представляет собой систему четырех квазилинейных дифференциальных уравнений первого порядка. Данная система не является гиперболической, поскольку имеет два семейства кратных вещественных характеристик, каждому из которых соответствует один собственный и один присоединенный вектор. Тем не менее, задача Коши для этой системы с гладкими начальными данными, при которых скорости характеристик (5) ограничены, локально однозначно разрешима. В основе численного решения задачи лежит построенная разностная схема (9), допускающая явную реализацию. Для определения порядка сходимости схемы проведено ее тестирование на точном решении (11). Выполнена серия численных расчетов, демонстрирующих влияние эффекта инерции на основные параметры пластического течения вне круглого и эллиптического отверстий. Из этих расчетов следует (Рис. 2, Табл.), что заметные отличия в решениях системы уравнений (7) при e = 0 и e ^ 0 проявляются в случае сравнительно больших скоростей пластического течения, заданных на границе отверстия, и достаточно большого значения коэффициента инерции e , определяемого плотностью и пределом текучести материала.

Работа выполнена в рамках программы фундаментальных исследований СО РАН № III.20.3, при финансовой поддержке Совета по грантам Президента РФ для поддержки ведущих научных школ (грант НШ-246.2012.1) и Президиума РАН (проект № 4.8).