К численному решению задачи Дирихле методом локально-канонического разбиения
Автор: Хубежты Шалва Соломонович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.5, 2003 года.
Бесплатный доступ
Применяются квадратурные формулы повышенной точности, аналогичные методу дискретных особенностей, для решения граничной задачи Дирихле на областях, ограниченных гладкими замкнутыми контурами. Доказывается существование решений приближенных систем, оценивается погрешность вычислительной схемы.
Короткий адрес: https://sciup.org/14318084
IDR: 14318084 | УДК: 519.64
Текст научной статьи К численному решению задачи Дирихле методом локально-канонического разбиения
Применяются квадратурные формулы повышенной точности, аналогичные методу дискретных особенностей, для решения граничной задачи Дирихле на областях, ограниченных гладкими замкнутыми контурами. Доказывается существование решений приближенных систем, оценивается погрешность вычислительной схемы.
Метод граничных интегральных уравнений, как известно (см. [1]), является одним из наиболее эффективных средств численного решения некоторых классов задач математической физики и механики. При этом, как было показано в [2], решение аналогичных задач на. основе аппроксимации сингулярных интегралов может обладать определенными преимуществами перед обычно рассматриваемыми схемами, основанными на. приближенном решении интегральных уравнений Фредгольма. Метод аппроксимации сингулярных интегралов в определенном смысле обладает некоторой возможностью увеличения порядка. точности схемы. Это обстоятельство и аспекты конструирования метода, дискретных особенностей (см. [2, 3, 4]) мы будем пояснять более подробно на. примере задачи Дирихле.
Пусть D - конечная односвязная область в плоскости комплексного переменного 2 = хУД, ограниченная замкнутым контуром Ляпунова. L, уравнение которого относительно дуговой абсциссы s есть t = t^ = х^ + iy^, 0 < s < I, f^ - заданная на. L (действительная) функция. Представление решения соответствующей задачи Дирихле в виде
U(x, у) =Re- f^dt Д G D, 1трД = 0), где рД - искомая действительная функция, приводит к граничному интегральному уравнению (см. [1; §61])
ДКИКеД [ ^-dt = Д^ (t0 G L). тгг у t-t0
L
Решение указанной задачи методом аппроксимации сингулярных интегралов заключается в аппроксимации уравнения (1) непосредственно на. основе замены сингулярного интеграла.
(^)(f0) = - [ ДД dt тег J t - to
L
его некоторым приближенным выражением. Конкретно, в этом качестве мы используем метод локально-канонического разбиения контура. L с использованием далее метода, дискретных особенностей, изложенного в [5]. Указанная схема, строится следующим образом. ”
Считая, что L — замкнутый (ляпуновский) контур на. комплексной плоскости, введем систему точек ДД23Д разбивающих L на. равные части. Зафиксировав произвольно и (1 ^ и ^ 2п) и положив to = тр, рассмотрим
1/ тгг J
L
t - т.
dt = (рДД + —
dt t-Tv
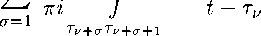
(подразумевается, что возрастание индексов в узлах соответствует положительному направлению на. L), причем под обозначением т8тр (s < р) понимается кратчайшая дуга, с концами т8,тр- т0 = т2п (rJ±2n = ту j = 1, 2,... , 2п). Далее, исходя из (1), подынтегральное выражение на. каждой дуге Ту+аТу+а+1 будем аппроксимировать линейным интерполянтом по узлам Ту+а, Ту+/+1. Что касается интеграла, по дуге Ту_1Ту+1, то в качестве интерполяционных узлов используем Ту_уТу^х обходя тем самым узел tVi который в данном случае будет контрольным аналогично методу дискретных особенностей (см. [5]). В результате получается следующая квадратурная формула, (см. [4]):
1 Г W^ X , / , ДДи-^-рДД (Д-Щщ) - (ДтД
— -----dt и <рД^ + Ду_2 + Pz/O)-- н VPvO + PvVO-------------
Тг J t Ту Ту — I Ту ТуИ Ту
L
2n—3
+ 52 ^T" + РиТачД
(7=1
^(Ty+a+l) - ^zv+tr + l Tv (z/= l,2,...,2n), где _ Ty+1 Ту- l _ Ty+j + l Ty+j j = 1, 2,... , 2n — 2. Pl/0" 2^ ’ P"+]" 2xi ’ Полученная формула. (3) является своеобразной модификацией метода, дискретных особенностей (см. [5])“ так как интеграл рассматривается на. дуге Ту_1Ту+1, а. параметр сингулярности to принимает значение Ту в середине дуги Ту-рГу^. В дальнейшем формулу (3), по определенному соображению, удобнее переписать так — ;----dt и Дту) + ) Ду+а +ру+(т+1)----------------,(4) тг J t - Ту Ту^а^х - Ту гДе Ту I 1 — Ту— 1 4/+? + ! — Tv4i PvTO =Pv-\- PM = ---X—---, PvT3 = --", j = -n, -n + 1,... ,n _ 1 (7- д -1, j д 0). Для сингулярного интеграла, в точке t0 G ТуТу+1, t0 Д т^+i воспользуемся формулой 1 f v№ х „ ^(^+<7+1) - Lny(^-to) • , dt ~ p(to) + / VPvTcr + PidTaTl) ,, Tl J t - to Ту+ст+1 - to L-nv^Vi О) — ^L^^pip'j (tg) — До (to)рДу) + ^i (to)^(^+1) ’ Mto) = ——-^-, ^i(to) = ———, to G tvtvVV, to ^ TvVV. Tv — T^+l Щу | — Tv Тогда, квадратурный процесс можно записать в виде (S^Hto) и p(to) + (QnZ/^)(to), t0 G т„т„+1, to Д т^, 1 < z/ < 2n, где (9п^)Ы = 52 (Pv+. +p„+a+1)?<^±ik^ „ Tv-\-a-\-i " К доопределению (QmzpMto) в точке т^+i (как соответствующего предельного значения) достаточно заметить уДу+Д - Lw(ip] to) _ Д-щ+1) - (Дту) Tv+l - to , Т„+1 - Tv го—тэ+i При этом непосредственным образом убеждаемся, что вообще VQn3^VT3^ Д VQn3^^ (Q2n,2n’)(T2n) = (Q2nO^)(To), Т0 = Т2п. В связи с этим, с целью построения заведомо непрерывной на. всем L аппроксимации (что существенно с точки зрения обоснования схемы), мы в дальнейшем, полагая IQnVHM = IQnjVHM, to G t3tjU (t0 Д 7j+i), j = 1,2,... , 2n, ( (^)(t0) « (5^)(t0), to EL, где (5П<Д(!О) = <Д10ЖММ Доказывается, что оценка, точности приближения (S 0), причем рм принадлежит классу Гёльдера с показателем /z, выражается формулой max|(SV)(t„) - (SM(to)l = О ||Уг|||НМ.(5) где. (^^((^о) — ^(to) + (Qn^)(to) (to G L), Ь11н(„) = max|<^(t) + sup ^^ /1^ (fi ^ ^),(5') ^L У^еь \t\-W которая справедлива, и для г = 0 и г = 1. Перейдем теперь к доказательству ряда, утверждений, относящихся к обоснованию изложенной здесь схемы. Обозначим через Н^Д (0 < /z < 1) пространство функций, удовлетворяющих на L условию Гёльдера с показателем р при соответствующем (5') определении нормы. Покажем что при достаточно болвшом п для (Яп^М^о) = (S'y)(t0) - (S„ при ip Е Н^Д (0 < а < 1) справедлива, оценка. (111 ть \ а_р ) Ит’Нящ) (0 3 < а). Действительно, полагая to Е т^т^-щ (1 < и< 2п), воспользуемся неравенством (7?п<р)(10) < ^So^HM - Е^ДЗорШо^ + \Luv где ^ш^-Д-УДД^»». лг J t -t0 Учитывая Lni/(l;tg) = 1, согласно теореме Племеля — Привалова. ([1; §18]) для первого слагаемого в первой части (7) нетрудно получить оценку Оф-Д |Ия(а) • Ко второму же слагаемому применим оценку (5) при г = 0 (/z = а). В результате получаем тах|(Дп^)(10) = О — |И1ящ) Д > 1)-соЕЬ \ / Далее, пусть НД2 Е L. В силу (8) находим \(,НпДД^ - (Я„<р)(12) = °(ДД|М|Н|Ч Slip q |Щ—#2|>Я/2 Д-М Для НД2 таких, что Н — 12 < h/2 можно при достаточно большом п считать НД2 G т3т]+1 U т]+1т]+2 (1 < / < 2п - 2). Полагая пока, что обе эти точки находятся на. одной дуге разбиения, воспользуемся для Д^ДД - (Вп^)(12) аналогичным (7) неравенством. Тогда, учитывая Фо(Н) ” Фо(^) — Ф1(Н) — ^1(^2) — Н — ^2 Т//+1 - Tv = ОДД^! - 12^, для рассматриваемого выражения нетрудно получить оценку №¥>№) - №у)(12)| = о Д - l2|^bhM. Случай, когда. НД2 находятся на. разных дугах ПП+Ь Tj+iTj+2; очевидным образом сводится к предыдущему. . Возвращаясь к уравнению (1) заметим, что в силу известных утверждений относительно его разрешимости и сингулярных операторов вида. (ЗД(10) (см. [2]), оператор К = I + l/2ReS0 (Я(/Д -Д НД\ 0 < р< 1) непрерывен и непрерывно обратим. В принятом в начале предложении ляпуновости контура. L аналогичное справедливо и в пространстве непрерывных функций. В дальнейшем наряду с уравнением (1), которое будем считать всюду ниже записанным в виде Кр = 1/2/, в пространстве Нф^ будем рассматривать (Яп^)(1о) = рДМ + |Re(Qn^)(to) = ^НМ. Для разрешимости уравнения (9) рассматривать соответствующие однородные уравнения ' ^(io) + l/2Re(Qn^)(io) = 0 (90) и докажем, что начиная с некоторого п они имеют лишь нулевое решение. Для этого воспользуемся утверждениями 1)-2) доказанными в [2]: 1) Пусть {Д} - любая последовательность натуральных номеров с условием jn/n Щ 0 (п Щ оо). Тогда, при любом v (1 < v< 2п) и стоДоД1 таких, что тТ+^ту+^ + х, ти+Хо,ти+Х1 G т^т^, справедливо —^ТД--= ~;J_A хМОДД/Д Д^оо), Т//+Ао О? ■ A 2ти(А0Ai) (Ю) ГДе wjnh = max Дж (Д - ж (7/)|, |у (Д - У Д)|} -^ 0 (п ^ оо). у-пез^^+аИ 2) При достаточно большом п имеем 1Ш1я(,3) = O(lnn)/i^(^„), где tpn — решение уравнения (9о), а Кр^Р-пЗ max l^J^n ^пМ - ^„(тД In - ТЛ9 U = Z7 + А, А к 0). Использование (И) вместе с (8) для <р„ (с заменой а на /3) дает max (Дп(р„)(10) = О КррРт?) рп —> оо). Кроме того, можно написать (М)(Д - №п^ = |Re(R„^)(i0). Отсюда, в силу (12) и замеченного выше об обратимости оператора. К находим, что равномерно относительно t0 G L выполняется <аДД) = О ( ) К^^Ф^ ^^°°Y (13) Теперь, используя (10), (13) можно показать, что при достаточно большом п уравнение (90) не может иметь нетривиальных решений. Для этого, очевидно, исходя из структуры сумм Q„, достаточно доказать, что начиная с некоторого п имеет место /гп/зДп) = 0. В дальнейших рассуждениях считаем указанную в утверждении 1) последовательность {Д} выбранной так, что для заданного р G (0,1) и любого б G (0,1] верно j9 In2 п -Д 0, п"5з9+5 -Д 0 (n Н- оо). (14) Переходя непосредственно к оценке Д^ДД, разделим множество узлов tVit^ = ту^\ на. j - Ц > jn, j - Ц < Д. Используя (13), получаем ДпДД - рпДД\ (\Дп\ max --=-----5--= О — щах ДДтр^ = О —з- Д^ДД Д -Д оо). и-^1>у Д-м \jU x^2n \ jn / , , В оценке соответствующего выражения при \j — v\ ^ jn, очевидно, достаточно ограничится j = и + А (А = 1,2,... 1 < jn< f, ! < j< 2п). Учитывая, что в силу (9о) ^„(т^+а) - <РпДД + -Re [(Qn^+A^nK^+A) - (Qn^nK^)] = 0,(16) разобьем суммы в выражениях ДД^рД ДД и ^ппдх^рДД^ соответственно на. Е^мЕ^иЕ^з-Е^.где 7 V^ Е ( I \ ^Дп+а+Д - РДД ( / . . , ) (^п) — / у kPv+a+l + Рп+Д, Tv^a^-Tv ДДы- Е w-.m»^-^^^., V 7 т^+^+1 - т^+А сгДХ — 1 а Еу^Еущ содержат суммы остальных слагаемых соответственно в ^п^ДДД и ^^+х^ДДплхУ Воспользовавшись в суммах Еу„1’Еу„з представлением (10), убеждаемся (учитывая 1тфДД = 0), что в получающихся в результате слагаемых главные члены оказываются чисто мнимыми, поэтому Ref q ~ УЁ • 1 ) ^Д — ОДод^ДН.прДДК ^|-з ~ ^ ЗпОДу^нД^рДД. \ Jn 4 7 <7=1 К (EJn4,EJn2)(^) применим представление (-(2j„ + l) п А <7=-(n-l) a=2Jn41j / -(2jn + l) п ^Pn+a+1 + Pn+a , Д V-^ Y-^ x------------+ Дп+Х - ТУ) X + У ^tx + ^ + l 1"v \ ( л\ —о1 1 1 У<7= —(n—1) <7—2jn + l ^(Tiz+a+l) - ^(т^+а) ДпЛаЛ\ - Tz/+A)(Tz/+ff+i - тД ’ заметив при этом, что сумма со множителем т^х - т„ в соответствующем представлении может быть оценена, выражением вида. ОД2Х^ max (р„(т„) 1^р^2п Д1/+а+1 + Piv+a') =2?п + 1 ^^^^Т1 si/+a| |si/± На основании этого, воспользовавшись соотношением (13) убеждаемся, что рассматриваемая сумма ^Тр+х - т^ — (2jn + l) п Е + Е а= — (п — 1) a—2jn + l (Piz+o-H + Ру+сг) ^(Ty+a+l) - ^(т^+д) (Ту+ст+1 - T^+AjtT^+^+i - Т„) ^(^n)’ Оставшуюся сумму в выражении Sj„4 —^jn2 ) (^п) представим в виде Аущ^Д + ^jnl^Tl'l — Py+2jn + l Ру-23п [^„(т^+а) - ^ДтД], TvVljn-W — ти ту-2зп— ту Pi/+2jn+2 __^_ у^ Ру+а-Н + Pv^a Ту^23^2 - TV ^^ Т^ + г - Tv Py—2jn — l Ty-2jn — ТУ + Ру—<т+1 + Ру—а Ту—(т+1 Tv \хДТу+Х^ - Pn^Y Очевидно Ajni(y„) = Of/i^A^ ^/г,^ (?„). Относительно Xjn2 заметим, что множитель для Ш^+аЬ^Ы) можно рассматривать как усложненную квадратурную сумму (см. [6]) для интеграла 1 f dt -кг J t-Tv' ln = L\T„_2jnT„+2jn (п^оо). Для соответствующего остаточного члена гп(?п), можно написать |гп(уп) = О(/г2) 52 ™ I,1 12 = ОШ 52 А = °^п^ ^ 0 Ьг ^ оо). (18) CT=23n + ltEn d Tv' a=2j„ + l(T Легко вычисляется, что (см. (10)) 1 = Т-И^ ~ Т-= 1 + In f 1 + = I + ОМ. кг] t-Tv кг Tv^2jnVV-Tv \ 1 - wJnh ] Последнее вместе с (18) дает Ау,12(^п) = [-1 + О(7пХ) + Otwy^JJ^nt^+A) - <£пЫ], гг -Д оо. В результате, с учетом (16) получаем Рп^+х") - РпМ 1 рДТу+х') - VnM \ту+х-ту\3 1 + М \ту+х-ту\3 +^О^п-5з^5НОи;3^п^п3Ы=01 1<А<ь, (19) где б (0 < б< 1) показатель в условии Ляпунова для контура L, еп —> 0 (п —> оо). На основании этого и (14), (15) следует требуемое утверждение НпДД = 0 при достаточно большом п. А это означает, что уп(10) = 0 - тривиальное решение для уравнения (90) начиная с некоторого п> по. Далее рассмотрим тождество ф-фп = ^К;ЧКп-К)К"Д. Из выше доказанного следует, что операторы Кп в пространстве НД) имеют непрерывные обратные. Тогда, на. основании оценки (6), учитывая, что у и у„ решения уравнений (1) и (9) при у) G НН (а > /1), имеет место (In2п \ , ДДД) Ь^зД. (20) Таким образом справедлива. Теорема. Пусть D - конечная односвязная область, ограниченная замкнутым контуром Ляпунова. L, /(f) - заданная функция на. L Действительная), удовлетворяющая условию Гёльдера НД) (0 < a< 1), тогда, вычислительная схема (9) для граничной задачи (1) при п > п0 имеет единственное решение фп и справедлива оценка. (20), где a > /3. Наконец отметим, что можно построить квадратурные формулы по методу локальноканонического разбиения более высокой степени точности. В частности, вместо интерполяции с двумя узлами можно взять три или четыре узла. В этом случае обоснование вычислительной схемы проводится аналогично, но при существовании соответствующих производных оценки будут более высокого порядка.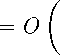
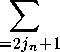
Список литературы К численному решению задачи Дирихле методом локально-канонического разбиения
- Мусхелишвили Н. И. Сингулярные интегральные уравнения.-М.: Наука, 1968.-540 с.
- Саникидзе Д. Г. К численному решению граничных задач методом аппроксимации сингулярных интегралов//Дифференциальные уравнения.-1993.-Т. 29, № 9.-С. 1632-1644.
- Нинидзе К. Р. О локальном каноническом разбиении в схемах численного решения задач плоской теории упругости//Тр. IX Международного симпозиума, Орел.-2000.-С. 329-332.
- Саникидзе Д. Г. О методе дискретных вихрей повышенной точности для числ енного решения одного класса сингулярных интегральных уравнений//Дифференциальные уравнения.-1998.-Т. 39, № 9.-С. 1-7.
- Лифанов И. К. Метод ситнгулярных интегральных уравнений и численный эксперимент.-М.: ТОО "Янус", 1995.-520 с.
- Никольский С. М. Квадратурные формулы.-М.: Наука, 1974.-224 с.


