К идентификации решений уравнения Риккати и других полиномиальных систем дифференциальных уравнений

Дифференциальные уравнения в частных производных очень важны для исследований в различных областях математики, физики, механики, химии, биологии и т. д. [1, 2]. В работах [3, 4] предложена унификация внешнего вида систем УрЧП. В работах [5–8] предложено сведение систем УрЧП к системам УрЧП меньшей размерности, в частности, к системам ОДУ путем их переопределения дополнительными уравнениями связи. Были предложены различные способы переопределения как отдельных систем УрЧП, так и УрЧП общего вида [5, 6, 9]. При редукции некоторых систем УрЧП в частности, унифицированных УрЧП или уравнений Навье–Стокса, на основе метода переопределения, изложенного в работе [10], возникают переопределенные параметрические системы полиномиальных ОДУ. Таким образом, исследование и нахождение решений полиномиальных систем ОДУ важно для получения решений УрЧП в явном виде.

Не всякую переопределенную систему ОДУ можно решить в явном виде методом редукции, в частности, если взять первый интеграл в качестве уравнения связи. Требуется найти такой способ решения систем УрЧП на основе метода переопределения, чтобы он мог работать и в случаях неполного их переопределения, т. е. когда прямой алгоритм нахождения решений не работает. Цель данной работы заключается в том, чтобы предложить способ преобразования полиномиальных систем ОДУ к линейным системам ОДУ. В частности, если коэффициенты в этих уравнениях будут постоянные, то решение находится в явном виде. На примере частного приема нахождения и исследования решения переопределенной системы из двух полиномиальных уравнений строится общий способ такого преобразования. В качестве дополнения исследуется уравнение Риккати. Указываются новые частные случаи, когда можно найти его решение. Также приводятся численные оценки о сложности данного метода при его практической реализации.

Рассмотрим следующую переопределённую систему ОДУ:

dx     ₂

— = axx + bx+c, dt 1        1       1

a₂ x ² + b ₂ x + c ₂ = 0,

где a 1 = a 1 ( t ) , a₂ = a₂ ( t ) ^ 0, b 1 = b 1 ( t ) , b₂ = b₂ ( t ) , c 1 = c 1 ( t ) , c₂ = c 2 ( t ) - дважды непрерывно дифференцируемые функции от t e [ 0, T ] , T >  0 . Пусть к системе (1), (2) поставлена задача Коши

1 ₁ =₀ = ^x 0 , ^x 0 ^eR .

Умножим обе части (1) и (2) на x . Тогда

-^ ( x ² ) = 2 a 1 x ³ + 2b 1 x ² + 2 c 1 x , a ₂ x ³ + b₂ x ² + c ₂ x = 0.

Обозначим

R = x , Q = x ², S = x ³.

Тогда уравнения (1)–(4) можно записать в виде dR

— = a1Q + b R + c, dt a2 Q + b2 R + c2 = 0, dQ = 2 a{S + 2bQ + 2cR, dt        1         1          1

a ₂ S + b ₂ Q + c ₂ R = 0.

Поставим к (6)–(9) задачу Коши

R t = 0 = ^x 0 , Q t = 0 = ^{( x} 0 ) , ^S l t = 0 = ^{( x} 0 ) .

Пусть R , Q , S – решение системы (6)–(9) с задачей Коши (10), определенное на отрезке [ 0, T ] . Обозначим

L = dR - a^ ² + bR + c , L ₂ = a₂R ² + bR + c ₂, M ₂ = Q - R ², M ₃ = S - R ³ .     (11)

1 _dt     1         1       1     2     2         2       2      2                   3

Делая очевидные преобразования, из системы (6)–(9) получим следующую систему уравнений относительно L ₁ , L ₂ , M ₂ , M ₃ :

a2 M2 + L2 = 0, a 2 M3 + b2 M2 + RL2 = 0,

• L 1 = a 1 M ₂,

dM2  dQdR

---—--2 R— — 2 a^^M^ + 2bM2 — dt     dt        dt      1   3      12

Делая очевидные подстановки, из (12)–(15) находим, что aR - b

Lj = ai M2, L2 = a2 ^M2 , M3 = a2

dM 2 dt

b 1 a 2 - b₂ a 1 a ₂

M 2 ,

Таким образом, мы видим, что, если R , Q , S – решение системы (6)–(9) с задачей Коши (10), определенное на отрезке [0, T], то, исходя из обозначений (11), из (16), (17) следует, что L1 = 0 , L2 = 0, M2 = 0 , M3 = 0 на отрезке [0, T]. Следовательно, R является решением (1), (2) с задачей Коши х^=0 = x0, x0 eR . Здесь мы учли известный факт из теории линейных ОДУ, что если коэффициенты непрерывны на некотором отрезке, то решение задачи Коши существует и единственно на этом же отрезке [11]. Уравнение (17) относительно M2 имеет только одно нулевое решение на отрезке [ 0, T ] с нулевыми начальными данными.

Решим теперь систему уравнений (6)–(9). Из (7) и (9) следует, что

Q = AR + B , S = CR + D .                          (18)

где

A = — b 2 . B = — с 2 . C = a ₂          a ₂

) ^{2 -} a 2 ^c 2 ) ⁽ a 2 ^{) 2}

D = b²^ ⁽ a 2 )

Подставим (18) в уравнения (6) и (8). Имеем

dR dt

= ( a 1 А + b 1 ) R + a 1 B + c 1 .

, dR ( dA         о r         L i dB           _T

A— =---+ 2aC + 2bA + 2c R +---+ 2a^D + 2bB dt ( dt      1        1        1)     ( dt       1        1

Из (20), (21) находим решение

R =

— + a AB + c A - 2 ^D - 2bB dt ^{1          1          1          1}

---a A2 — b^A + 2 a^C + 2bA + 2 c dt 1          1           1          1          1

Решение (22) должно удовлетворять (20) или (21), а также R , Q , S из (18) должны быть со- гласованы при t = 0 по формулам (10), т. к. мы решаем (6)-(9) с задачей Коши (10). Тогда по формулам (5) определяется решение исходной системы (1), (2) с задачей Коши x^_ = x0, которая не может быть произвольной для переопределённой системы ОДУ. Фактически решение нелинейной переопределенной системы уравнений (1), (2) мы свели к решению переопределенной системы линейных уравнений (20), (21). Если подобрать a , b , с таким образом, чтобы знаменатель в формуле (22) равен нулю, то R находится из решения задачи Коши для линейного дифференциального уравнения первого порядка, которое может быть найдено в общем виде [11].

Уравнение (1) называется уравнением Риккати. Если известно одно из его частных решений, то находится общее решение этого уравнения в явном виде [12]. Зафиксируем коэффициенты a1 , b1 , с1 в уравнении (1). Если мы затем подберем коэффициенты a2 , b2 , с2 в уравнении (2), чтобы выражение (22) было частным решением (1), то мы найдем общее решение уравнения Риккати. Однако выкладки показывают, что коэффициенты можно подобрать не для произвольных a1 , b1 , с1 . Доказано, что общее уравнение Риккати нельзя получить в виде конечной формулы для любых коэффициентов a1 , b1 , с1 [12]. Однако его можно найти в многих частных случаях, если особым образом выбрать параметры a1 , b1 , с1 . В уравнении (2) вместо квадратного многочлена можно взять многочлен любой другой степени и получить новые случаи, когда можно найти частные решения (1), (2).

На основе приема, использованного в данном примере, предложим следующий метод нахождения решений полиномиальных систем ОДУ. Рассмотрим общий случай системы ОДУ из m > 1 уравнений от m неизвестных вида n1n2

dx = Х2-X 4,...,.)(x) A x 2) l2-( xm) m .(23)

i"1 =012 =0

i '1 = 0 i 2 = 0 l_m = 0

Дополнительными уравнениями связи (24) могут быть, например, первые интегралы системы (23), которые можно получить методом преобразования к каноническим уравнениям Гамильтона, изложенным в [8] (см. Приложение С). Умножим обе части уравнений (24) на выражения (Xj)71 • (x2)72 ■■■ (xm)jm , j1 = 0...N1,... jm = 0...Nm. Получим уравнения вида n1n2

P, ( X,... Xm, t )=EE ... E aiij^.)( Xj)  7 •( X2 ) '2 ’' 2 •••( xm )"' 'm = »•(25)

'1 =0 '2 =0

'1 =0 '2 =0

где    QP =( xl ) q1 •( x2 ) q2 •••( xm ) qm , e = в( q^-qm ) ,    qj = 0...(N1 + n1) ,— qm = 0...( Nm + nm)

Qp(o o) = 1. Учитывая (23), имеем также dQP{ j1,... jm) _ .  /   \j1-1  dx1  .   jj2    /    jjm        /   V1  /   y'2     . I    ym-1  dxm_

-----It-----= j1 •( X1)    •’^•(X2 )  ”’( xm )   + ...+ (X1)  •( X2 )  ••• jm •( xm ) '~cU = m  n1n2

=E E E... E      .'2....'.,) (X1) ■7 • • • (Xl)'j • • • (xm )'m j = l=1 '1 =0 '2 =0

m  n1n2

= E E E ... E jla( '1, '2,...'m ) QP(( '1 + j1),...('' + j, -1)...('m + jm )) ’   j1 = 0...N1 ,. jm = 0... Nm •

'=1 '1 =0 '2 =0

Количество мульти-индексов в = в ( q,..q_m ) (количество неизвестных в уравнениях (26), (27)) равно N S = ( N₁ + n₁ + 1 ) • • • ( N_m + n_m + 1 ) . Количество линейных обыкновенных дифференциальных уравнений (26), (27) равно N H = ( 1 + n )( N ₁ + 1 ) • • • ( N_m + 1 ) . Выберем N_k , k = 1 ... m так,

_  . _                             ,           (N ■1)      (Nm +1).

.

Тогда

чтобы  NH > NS, например, следуя работе [10],  ------ *...*  ------- * N * — n1            nmn

^N H > ( ^{n + 1} ) ^П 1 ••• n m

n

[10]. При m = 10, n = 1, n ₁ =

= n ₁₀ = 2 имеем N H > 2•Ю¹³, N * 10•

Достаточные условия (но не необходимые) для того, чтобы системы (26), (27) и (23), (24) были эквивалентные, могут быть найдены аналогично примеру из части 2.

Таким образом, мы имеем линейную переопределенную систему ОДУ (26), (27), решить которую гораздо легче, чем исходную систему (23), (24) (см. пример из части 2). Причем, если коэффициенты в (23), (24) постоянные, т. е. не зависят от t eR , то решение может быть найдено в явном виде [11]. Значимый пример использования данного метода приведен в работе [13].

Рассмотрим общий случай системы ОДУ из p >  2 уравнений от m неизвестных вида:

n (         dX,dX

' 1 = 0 ' 2 = 0 m = 0 j 1 = 0 j m = 0                        <  dt ^

im dm I  •(X1)’-(Xm j = 0 ,(28)

где    41.'2....'m X j1:j2-j )= ^^Л'г-а; )(Ы^,,)(t ) ■ t еИ •    '1 = ^'^ -   -m = nm ■    '

— j_m = 0... k_m , l = 1... p . К таким системам с помощью метода редукции [7, 8] можно преобразовать уравнения Навье–Стокса [10] или унифицированные уравнения из статей [3, 4], причем они будут с коэффициентами, не зависящими от t e R . Кроме того, систему полиномиальных уравнений (28) можно переопределить с помощью метода, изложенного в статье [10]. Обозначим

—s- = U_s, U ' = L, s = 1... m , L _o = 1.

dt     s dt     s0

Тогда в новых обозначениях

1 1 = 0 1 2 = ⁰   I m = 0 j 1 = 0 j m = 0

H « ( O p ) = 11 ... 11.. 1 a it i 2

ⁱ 1 = ⁰ i 2 = 0   i m = 0 ^j j = ⁰   j m = 0

где         Q e = L s ( U 1 ) q ¹ ■■■ ( U m ) q^m ■ ( X 1 )'

q 1 = 0... ( N + n 1 ),... q m = 0... ( N m + n m ) , тывая обозначения (29), имеем также ^dQ e ( 0, q,... c_m , d 1 ,... d_m ) _

O^                           = 0 ,    (32)

r ₁

■■■( xm ) rm ,        в = e(s, q1.... qm. r1,- rm ) ,        s = 0...m , r = 0...(K1 + k1) ,... rm = 0...( Km + km ) , Oe(0,0...0)= 1 . Учи-

dt

d [ ( U 1 ) ^{C 1} ■■■ ( U m ) c m ■ ( X 1 ) d ¹ ■■■ ( x . ) d m

= c 1 ( U 1 ) c ^{1 — 1 U} ■ ■ ■ ( U m ) c m ( X 1 ) d ¹ ■ ■ ■ ( X m ) ^dm + ... + ( U 1 ) c ¹ ■ ■ ■ c m ( U m ) c m ^{— 1} U- ( X 1 ) d ¹ ■ ■ ■ ( X m ) ^dm + tt

+(U1)c1 ■ ■■(Um)cmd1 ■(X1)d1—1 ■ d^■■(Xm)dm +... + (U1)c1 ■ ■■(Um)cm (X1)d1 ■ ■■dm ■(Xm)dm —dm-- tt

= C 1 L 1 ( U 1 ) c ^{1 — 1} ■ ■ ■ ( U m ) c m ( X 1 ) d ¹ ■ ■ ■ ( X m )^ + ... + ( U 1 ) c ¹ ■ ■ ■ C m ( U m ) c m

— I

4,.( X 1 ) ^{d ,} ... ( X m ) ^dm +

+ ( U 1 ) c ^{1 + 1} ■ ■ ■ ( U m ) c m ■ d 1 ■ ( X 1 ) d ^{1 — 1} ■ ■ ■ ( X m ) + ... + ( U 1 ) c ¹ ■ ■ ■ ( U m ) c m + 1 ( X 1 ) ' 1 ’ ” d m ’ ( X m ) d m — 1

Количество мульти-индексов в = в ( s , q 1 ,... q_m , r 1 ,... r_m ) (количество неизвестных в уравнениях (32), (33)) равно

NS =(m + 1)(N1 + n1 +1)■■■(Nm + nm +1)(K1 + k1 +1)■■■(Km + km + 1) •

Количество линейных обыкновенных дифференциальных уравнений (32), (33) равно

N_H = p ( m + 1 )( N 1 + 1 )^-( N m + 1 )( K 1 + 1 )-( K m + 1 ) +

+ (N1 + n1 )",(Nm + nm )(K1 + k1 + 1)■■■( Km + km + 1) •

Выберем N_s , K_s s = 1... m так, чтобы N_H >  N_S , например, [10]

( N il . ... ^W m l! .Wil . ... „W m ll. N , N . 2 ml [f m + 1 1 p — 1’ .

n1             nm         k1             km                 / L< m 7_

Тогда

NH -

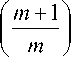
Pn l ••• n m k l ••• k m

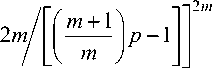
При p = 11, m = 10,

n 1 = ... = n₁₀ = 2, k 1 = ... = k ₁₀ = 2 имеем N_H - 4-10¹¹. N ^ 1,7.

Таким образом, мы имеем линейную переопределенную систему ОДУ (32), (33), решать которую гораздо легче, чем исходную систему (28). Причем если коэффициенты в (28) не зависят от t eR, то решение может быть найдено в явном виде [11]. Чтобы получить еще уравнения, можно продифференцировать (30) по t и использовать обозначения (29). Достаточные условия (но не необходимые) для того, чтобы системы (28) и (32), (33) были эквивалентные, могут быть найдены аналогично примеру из части 2.

Заметим, что помимо уравнений (32), (33) должны выполняться еще Ns (34) уравнений ви- да:

Q e = L s U ) q -(U m ) q m • ( X 1 ) r ¹ ••• ( x_m ) r m ,                         (36)

^s = 0... m .        q 1 = 0... ( N 1 + ⁿ 1 ) ,. q m = 0... ( ^N m ^{+ n} m ) ,        r 1 = 0... ( K 1 ^{+ k} 1 ) ,- r m = ⁰- ( K m ^{+ k} m ) .

Q ^_oo о) = 1. В случае, если общее решение линейной системы ОДУ (32), (33) содержит некоторый произвол [11], например, если число независимых уравнений в (32), (33) меньше числа неизвестных N S , то предположительно его можно определить с помощью дополнительных соотношений (36) обычным методом редукции переопределенных систем ОДУ [7, 8]. Аналогично можно поступить, если общее решение линейной переопределенной системы ОДУ (26), (27) также содержит некоторый произвол.

Заметим, что систему уравнений (28) можно записать в виде dx dx

V         dt dt j n1   n2     nmk1      km                                      i1

I..1 ^m)( ^-j. )I X 1 -I dm l  •( X1 )' •••( Xm J = 0.(37)

i 1 = 0 i 2 = 0   i m = 0 j 1 = 0 j m = 0                        V ^{dt j}      V dt ^j

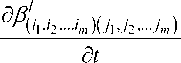
где

alii            ,4= alii  i у       m( t ) . t eR . i = 0... n ,       i_m = 0... n_m . j = 0... k, .

... j_m = 0... k_m . l = 1... p . Систему уравнений (37), (38) можно рассмотреть как систему из p + p ( n 1 + 1)- - ( n_m + 1 )( k 1 + 1 ) — ( k_m + 1 ) уравнений и m + p ( n 1 + 1)- ^ ( n_m + 1 )( k 1 + 1 ) ^-- ( k_m + 1 ) неизвестных ^X 1 , ... ^x m . в < , i₂ ,...,_m )( j , j ,... j_m ) . i 1 = 0.. n j , ... im = 0... n m . ^J 1 = 0... ^k 1 , . J m = 0... ^k m . l = 1- p •

Заметим также, что для системы ОДУ (28) не предполагается изначально, что p - m . В частности, можно взять p <  m . Систему уравнений (37) можно рассмотреть как недоопределенную систему полиномиальных уравнений с постоянными единичными коэффициентами. Как показано выше, эту систему уравнений можно преобразовать к переопределенной линейной системе ОДУ с постоянными коэффициентами вида (32), (33). Допустим, что решение этой линейной системы содержит некоторый произвол [11], например, если число независимых уравнений меньше числа неизвестных. Тогда предположительно его можно определить с помощью дополнительных уравнений (38), а также с помощью уравнений, аналогичных уравнениям (36), обычным методом редукции переопределенных систем ОДУ [7, 8].

В данной статье мы предложили способ преобразования полиномиальных систем ОДУ к линейным системам ОДУ. Но на практике этот способ довольно сложно реализовать. Количество линейных уравнений, которые необходимо решить, быстро растет с увеличением количества уравнений в исходной системе полиномиальных уравнений. Численные оценки дают цифру в более чем миллиард уравнений. Однако наш результат может быть интересен с теоретической

Зайцев М.Л., К идентификации решений уравнения Риккати и других Аккерман В.Б. полиномиальных систем дифференциальных уравнений точки зрения. Как было указано выше, уравнения Навье–Стокса [10] и унифицированные уравнения из статей [3, 4] с помощью метода редукции преобразовываются к переопределенным системам полиномиальных ОДУ с постоянными коэффициентами. Решение таких нелинейных систем с помощью нашего метода может быть представлено в виде суммы очень большого, но конечного количества нарастающих и затухающих колебаний во времени с разными частотами, которые теоретически можно вычислить. Амплитуды этих колебаний зависят от начальных данных нелинейно. Однако представить даже это решение в явном виде крайне затруднительно, и тем более его посчитать даже на ЭВМ. Возможно, из-за этой особенности до сих пор возникают сложности при моделировании уравнений Навье–Стокса. Известно, что численное решение уравнений Навье–Стокса начиная с некоторого момента времени становится нестабильным и переходит в очень сложное беспорядочное колебательное движение, которое невозможно отследить. Предположительно в этот момент начинают играть роль все колебания, сумма которых составляет общее решение, которое мы предлагаем в данной статье. Аналогичное можно утверждать и в отношении унифицированных систем УрЧП, полученных авторами ранее в работах [3, 4].

Рассмотрим общие уравнения в виде [3, 4]

dUi

---— =---—, i = 1...m, ц = 1...m, v = 1...p , i > ^,                      (А.2) дx„ дX: LL l дSv         i• i

(А.3)

Uv = —- , v = 1...p, i = 1...m. дxi где x = ( x1,... xm )g Mm. Пусть

Ak,(j1,... Jp)     }(tA k^   lUs\ks ---mU™^ jV

L^ =—- , J = 1...p , l = 1...m, h = 0...m , L0 = 1.(А.5)

^{д x} h

Умножим       обе       части       уравнений       (А.4)       на       выражения a1           alam

H Q„ У V     _A ^{k ,( J} '¹”" ^Jp )   ( _x) Q , ,              ,= 0 (А 7)

^{a (} ^ )    1 A m - - 1    ( k * ¹’- k' s ,... k p У  ^в ( i , J , _h , ( k J + a j ) ,... ( k s + a s ) ,.... ( k ^ + a p ) , ( J + b 1 ) ,... ( J p + b p ) )       ’        '^

1 lm

Qp — L,(U1) 1 -(Us) s -(um) p •(S1)r -(Sp)rp , (А.8) в — в(i, j,h,qb-qP,ri,...Гр), j — 1...p, i — 1...m, h — 0...m, l — 1...m, s — 1...p, qS — 0...(nS + rs), ri = 0...(K1 + w1),... rp — O...(Kp + wp), Qe(i,j,0,..0) = 1. Учитывая обозначения (А.3), (А.5) и (А.8), имеем также

^{5 Q} e ( 1,1,0, c ¹,... c m , d 1 ^d x ,

~   - x [ ( u 1 ) c ¹"' ( u S ) c s   'Um ) c m ' ⁽ S 1 ) d '"( ^s p )

d p

= cU ( u 1 ) c ^{1 - 1} ■" ( u s ) c s “( U" m ) c m ■ ( S ' ) d "'( S p ) d p + ...

... + ( u 1 ) c ¹ ■ ■■ ( U ) ^cs ■■ p u u m ) c^{p - 1} d u p ■ ( S 1 ) ^d1 ■ ■■ ( S p ) ^dp +

1V1  {т^  mU"1^ d(^}d1-1 dS1

+ ( U1 ) •••( Us )  -\ Up )   -d1 (S1)    dX^’ ”(Sp )

... + ( u 1 ) c ¹ ■ ■■ ( u s ) c ^S - ■■ ( u p ) c m ■ ( S 1 ) r ¹ ■ ■■ d 1 ( S p ) ^{dp - 1} d ^{S p} = d x^

-11111 т?1 V 1 hcs\s mPn\p ^Ad1

= c1L, ( U1 )    •••( Us )  •"( Up )   ■( S1) •"( Sp )

... + ( U 1 ) ¹ ■■■ ( U ) ^s ■■■ c m ( u p ) ^p    L ,   ■ ( S 1 ) ^d1 ■■■ ( S p ) ^p +

+ ( U 1 ) c ¹ ■■■ ( u s ) c ■■■ ( u p ) c m ■ d 1 ( S 1 ) d ^{1 - 1} u , ■■■ ( S p ) ^dp + ...

1V1   lri!\^ iiAp Isld     d p

... ⁺ \ ^U 1 ) ••• ( ^U s )   ••• ( ^U p )    ■ ( ^S 1 ) ••• ^d 1 ( ^S p )

cQ                 +...+cnQ+

(А.9)

Уравнения (А.2), (А.3) в обозначениях (А.8) можно записать в виде

Q e ( i , v ,Ж....0Д...0 ) ^— Q e ( Д , v , i ,0,....0,0,...0 ) , i ^{— 1}... ^p , Д ^{— 1}... ^p , i >  Д , ^{v — 1}... p ,           ⁽А.1⁰⁾

^d Q e ( 1,1,0,0,...,0,... r_v — 1,...0 )

Qi        ,          4—-----¹------------------ , v — 1... p , i — 1... P .             (А.11)

в ( 1,1,0,0,... q V — 1,....0,0,...0 )                    d x.

Количество мульти-индексов в — в ( i , j , h , q ¹,... q P , r ₁,... r_p ) (количество неизвестных в уравнениях (А.7), (А.9) - (А.11)) равно

N_S — ( P ² p + 1 )( N ¹ + r ¹ + 1 )-( N m + r m + 1 ) ( K ₁ + w ₁ + 1 )-( K_p + w_p + 1 ) .            (А.12)

Количество линейных дифференциальных уравнений в частных производных (А.7), (А.9) -(А.11) равно

N H — Z ( m ² p + 1 )( N 1 + 1 ) ’ ” ( N m + 1 ) ( K ₁ + 1 ) ■ ■ ■ ( K_p + 1 ) +

+ m(N ¹ + r ¹У ■■ ( N p + rmYK + w_Y + 1) ••• (K_m + w_m + 1) + m ⁽ m ^{+ 1 ) p} .        (А.13)

11     pp  1  1      m  m

Выберем l — 1... m , s — 1... p , N^l_s , K ₁,. K_p так, чтобы N H >  N_S , например, [10]

ОМ. .им .( k u) . .M)_,v ~ ... ~~^ ... ^~ N , ^r 1 ^{1              r} p^{m          w} 1              ^w p

(А.14)

(А.15)

(А.16)

p(m +1)( m2p - m +1) n ^r^—■-----4.

(Zm2 p - m2 p + Z + m -1)

Тогда

N H >  r ¹ - r p W ••• w_p [ Z ₍ m ² p + 1 ) N ^{( m + 1 ) p} + m ( N + 1) ⁽ m ^{+ 1 )} p ] + m ⁽ m ' 1 ) p .

При Z = p = 2, m = 2, w 1 = ... = w p = 1, r ¹ = ... = r m = 1 имеем N H >  1,05 • 10⁵, N « 4.

Таким образом, мы имеем линейную переопределенную систему УрЧП (А.7), (А.9)–(А.11), решать и исследовать которую гораздо легче, чем исходную систему (А.1)–(А.3). Причем, если коэффициенты в (А.4) не зависят от x = ( x 1 ,... x_m )g R m , например, уравнения Навье-Стокса, то решение некоторых поставленных для них задач может быть найдено в явном виде [1, 2, 11]. Чтобы получить еще уравнения, можно продифференцировать (А.4) по x i , i = 1... m и использовать обозначения (А.3) и (А.5).

Учитывая соотношение (А.2), можно, исходя из определения (A.2), (A.5), (А.8), выписать еще уравнения:

r_p = 0... ( K_p + w_p ) . Их количество равно

1 m ( m - 1 ) p ( N ¹ + r ¹ + 1 )-( N m + r pm + 1 ) ( K 1 + w 1 + 1 ) — ( K_p + w_p + 1 ) .       (А.18)

Система линейных УрЧП (А.7), (А.9)–(А.11), (А.17) содержит все решения исходной системы УрЧП (А.1)–(А.3). Кроме того, мы имеем еще NS нелинейных соотношений, следующих из определения неизвестных Qp (А.8). Их можно использовать в том случае, если решения системы уравнений (А.7), (А.9)–(А.11), (А.17) будут содержать некоторый произвол. Например, применить метод редукции переопределенных систем УрЧП.

Фактически здесь мы предложили способ переопределения системы УрЧП (А.1)–(А.3), если выполняется (А.4). Продифференцируем (А.1) по xm . Имеем, dUd

(А.19)

(A.20)

У АУ —s + У Bk —L + Сk = 0, l,s                           i, l, s     dxm    i где k = 1...Z, l = 1...m, s = 1...p, i = 1...p и

Ak   '"'/k   Bk ^Hk Ck ‘H l,s   dU!s , i     5Si  ’

Систему уравнений (А.2), (А.3), (А.19) от неизвестных функций U_s ^l , S_i , A_l ^k _{, s} , B_i ^k , С ^k можно преобразовать к недоопределённой системе УрЧП вида (А.1) – (А.4), которую все равно указанным выше способом можно переопределить. Кроме того, мы имеем также дополнительные в общем случае нелинейные уравнения (А.20). Данный способ переопределения можно комбинировать со способом переопределения, изложенным в статье [10].

^ - B “ u

(B.5)

(B.6)

d t     д в

Подставим (В.3) в (В.1). Тогда

H ( u, p + B t ) = 0.

Таким образом, формально мы имеем переопределенную систему (В.5), (В.6) из 2 n дифференциальных уравнений и n неизвестных u = ( u ₁, u ₂... u n ) . Согласно гипотезе об универсализации решения задачи Коши для переопределенных систем дифференциальных уравнений, изложенной в работе [4], решение системы (В.5), (В.6) может быть представлено в виде:

u = G t , P,B,u|

1 1 = 0

d u

d u

’ d t t = o ’ d ₽

д ²u t = o ’ ^d t ^д в

, t=0

,

(B.7)

Пусть нам известны значения функций (В.4), при некотором в = в0 =( $, в2 —в) и t = 0. Пусть при в = в0 =( в0, в0 —Pm) и t = 0 выполняется dH du

* 0.

(B.8)

(B.9)

(B.10)

--+ — = 0, —    = -l— I — du dt   dt       dt t=0 в=в0 v du J dt dH du  dH „du        fdH Vd

+   = 0, du dв   dв      dв t=0,в=в0    l^ J5

Таким образом, по формуле (B.7) в явном виде может быть определено значение функций u = u ( в₀ + B t ) . Параметры B = ( B ₁, B ₂... B_m ) и переменную t можно варьировать. Мы видим, что если известно частное решение уравнений (В.1) при a = в 0 , то будет известно в явном виде решение (В.2) в некоторой окрестности точки β⁰значений параметра α .

Рассмотрим общий случай переопределенной системы из (m + p) алгебраических уравнений от m переменных n1n2     nm

i i = 0 i 2 = 0 i m = ⁰

где at .  . ^eR - параметры, l = 1... ( m + p ) . Соответствующая система (В.5), (В.6), построенная

для уравнений (В.11), будет иметь вид (А.1) – (А.4). С помощью введения дополнительных функций можно даже «сделать» коэффициенты в (А.4) постоянными целыми числами (см. (37), (38)). Тогда предположительно , решив эту систему в явном виде один раз, можно получить формулу для решения системы (В.11) в общем виде.

Если в уравнениях (В.11) al .  . x = at .   . x ( t ) , t eR , то, продифференцировав по t урав-

нения (В.11), получим систему уравнений вида (28). Для системы уравнений (28) мы привели гипотезу о нахождении её решений в явном виде (см. (37), (38)). Достаточно только знать решения системы уравнений (В.11) при t = 0.

Аналогичную теорию можно применить для следующей системы уравнений:

Е А .к ^j , .^j ) ₍ t )( x 1 ), ,₍ x 2 ,   ... ( X p ) ■ , ( _{U 1} ) j ,„ u u  ) ^jp ( S 1 ) k ... ( S p ) k p = 0,   (B.12)

• k i ,... k p ,             ⁽ 1 .... p )

• i ₁,... i_p , j ₁,... j_p

Sl = sh(xl), l = 1...p, t eR . Для этого достаточно заметить, что 22    22

• ( du )         id J dxi 1 L - d x       dxi i Л /   \2 \i dxi I ,   .„

I — l - I = cos²⁽ X i ) I — l - I = ( 1 ^- sin²( Xi ) ) l — l - I = ( 1 ^- ( U i ) l | — l - I , ^l = 1... p ,     (B.13)

• V dt J             V dt J ^{v            7} V dt J \         'V dt )

22    22

| — | = ch²( x ) | d ^ | = (1 + sh²( x )) | dx- | = (i + ( S )² | d ^ | , l = 1... p .     (B.14)

V dt J          l V dt J X       ' l'/V dt J (   ( l) \ dt J

Система уравнений (B.12)-(B.14) от неизвестных x l , u l , S l , l = 1... p . имеет вид системы уравнений (28).

Рассмотрим систему ОДУ следующего вида:

d x

— = F (x,g (t, a) ,a),(C.1)

Рассмотрим автономную систему ОДУ вида dx = F (x,g (t, a) ,a),(C.3)

а т

= 1(C.4)

dT с задачей Коши xlT=0 = x0 (a) , tT=0 = 0 •

Рассмотрим функцию

n

H ( x, t , p, p_t , a ) = ^ F i ( x,g ( t , a ) , a ) P i + p_t

(C.6)

i = 1

,             .

d r   d p  d rd

d p_ д H    dp-- _dH_

,                    •(C.8)

dr    dx     dTд где поставим задачу Коши

Pj\r=0 = 1, p. T—о = 0 • j =!-".(C.9)

Как известно, система (С.7), (С.8) является гамильтоновой. Функция (С.6) является ее пер вым интегралом. Следовательно, с учетом начальных данных (С.5) и (С.9) имеем nn

X ^F i ( ^x,g ( t ,a ) ,a ) P i + Pt = X ^F i ( ^x о ( a ) ,g ( ^0,a ) ,a ) .                (С.10)

i = 1                                            i = 1

Из уравнения (С.4) с учетом начальных данных (С.5) следует t = т. Следовательно, сделав обратную замену переменных, уравнения (С.7) преобразовываются к виду (С.1) с задачей Коши (С.2), а уравнения (С.8) записываются в виде dp_ дH dp--_дИ_

• •                 •                                       (C.1¹)

dt     dx   dt     д t где поставим задачу Коши

P j[ — о = ¹ • P t l t — о = ⁰ • ^j = ^ n .

(C.12)

В итоге мы имеем систему уравнений (С.1), (С.11) с задачей Коши (С.2) и (С.12), для которой выполняется дополнительное соотношение (C.10).

^{d x} m

д^  d S,

д x 1 д X i    д x m _ 1

m

,

(С.13)

i = 1... m _ 1, v = 1... n , k = 1... n .

(С.13), то оно является решением параметрической системы ОДУ вида (С.1)

^{д Y}v _ mm W = Fv ^{д x} m

. S S  J S^

д X 1     д x,    д x m _1

m

,

(С.14)

i = 1... m — 1, v = 1...n, k = 1...n, где (x1,...xm_1) - параметры, дSv/дxi, i = 1...m -1, v = 1...n - фиксированные функции.     Сле довательно, для системы (С.14) можно применить изложенную выше теорию: дополнить дополнительными неизвестными и построить дополнительное соотношение вида (С.10). В сущности, мы получаем переопределение системы УрЧП (С.13) с учетом начальных данных. Если система УрЧП (С.13) имеет вид (А.1)–(А.4), то переопределенная система будет такого же вида.

Фактически, данный прием является частным случаем следующего подхода. Введем следующую неизвестную функцию:

W = C f V V V   ^{д S} 1   ^{д S} k    ^дS n   у _Y 1                    1

I             a x    ^{д x} i   ^{д x} m _ 1          J

Продифференцируем (С.15) по x_m и подставим выражения для производных от неизвестных

S v = S v ( x ) , v = 1... n по x m из (С.13). В результате получим некоторое уравнение вида

W X     , dSi  dSk   S S    S

(С.16)

Q S1 ,■■■ Sk ••• Sn ,      ,                          •            , x x1 ,••• xi dxm-1     I             dX1    dXi   dxm-1  dxi

Если рассмотреть систему УрЧП (С.13), (С.16), то она, очевидно, имеет дополнительное со- отношение в виде интеграла

\               dSx   8Sk    dSnI

(С.17)

W ^- G ^S 1 ^,••• S k ••• S n ,—^L,... — •••  ---- ,^x 1 ^,••• x_m 1 = Const .

I              8x1    8xi   8xm -1

• 1.    Тихонов, А.Н. Уравнения математической физики / А.Н. Тихонов, А.А. Самарский. – M.: Наука, 1966. – 724 с.

• 2.    Курант Р. Уравнения с частными производными / Р. Курант. – 1964. – 830 с.

• 3.    Зайцев, М.Л. Преобразование систем уравнений в частных производных к системам квазилинейных и линейных дифференциальных уравнений. Их редукция и унификация / М.Л. Зайцев, В.Б. Аккерман // Математическая физика и компьютерное моделирование. – 2018. –Т. 21, № 1. – С. 18–33.

• 4.    Zaytsev, M.L. Unification of Solution of the Cauchy Problem for Overdetermined Systems of Differential Equations. Version 3 / M.L. Zaytsev, V.B. Akkerman // Research Gate. March. – 2019.

• 5.    Аккерман, В. Б. Снижение размерности в уравнениях гидродинамики / В.Б. Аккерман, М.Л. Зайцев // Журнал вычислительной математики и математической физики. – 2011. – Т. 51, № 8. – С. 1518–1530.

• 6.    Зайцев, М.Л. Гипотеза об упрощении переопределенных систем дифференциальных уравнений и ее применение к уравнениям гидродинамики / М.Л. Зайцев, В.Б. Аккерман // Вестник ВГУ. Серия: Физика. Математика. – 2015. – № 2. – С. 5–27.

• 7.    Зайцев, М.Л. Еще один способ нахождения частных решений уравнений математической физики / М.Л. Зайцев, В.Б. Аккерман // Вестник ВолГУ. Серия 1, Математика. Физика. – 2016. – № 6 (37). – С. 119–127.

• 8.    Зайцев, М.Л. Редукция переопределенных систем дифференциальных уравнений математической физики / М.Л. Зайцев, В.Б. Аккерман // Математическая физика и компьютерное моделирование. – 2017. –Т. 20, № 4. – С. 43–67.

• 9.    Зайцев, М.Л. Задача обтекания и сокращение размерности в уравнениях Навье–Стокса / М.Л. Зайцев, В.Б. Аккерман. // Труды МФТИ. – 2015. – Т. 7, № 3. – С. 18–30.

• 10.    Zaytsev, M.L. Алгоритм нахождения решений переопределенных систем дифференциальных уравнений в явном виде / M.L. Zaytsev, V.B. Akkerman // Research Gate. July. - 2020.

• 11.    Федорюк, М.В. Обыкновенные дифференциальные уравнения / М.В. Федорюк. – СПб.: Лань, 2003. – 447 с.

• 12.    Егоров, А.И. Уравнения Риккати / А.И. Егоров. – М.: Физматлит, 2001. – 318 с.

• 13.    Зайцев, М.Л. Преобразование уравнения Риккати и других полиномиальных ОДУ к системам линейных ОДУ в явном виде / М.Л. Зайцев, В.Б. Аккерман // Вестник ТГУ. Математика и механика. – 2021. – № 72. – С. 5–14.