К методике определения сопротивления материалов импульсному нагружению
Автор: Купершляк-Юзефович Георгий Марианович, Шкербин Юрий Владимирович, Исаева Наталия Юрьевна
Рубрика: Контроль и испытания
Статья в выпуске: 33 (166), 2009 года.
Бесплатный доступ
Приведена оригинальная методика синхронного измерения продольной силы и деформации в контрольном сечении стержня-образца при распространении упругопластической волны. По экспериментальным зависимостям напряжение-деформация-время алюминиевых сплавов и аустенитной стали выявлены два последовательных вида деформирования: упругопластическое при постоянной скорости нагружения и динамическая ползучесть при уменьшении скорости нагружения и разгрузке.
Напряжение, деформация, скорость, импульсное нагружение
Короткий адрес: https://sciup.org/147151478
IDR: 147151478 | УДК: 531.78.2
Текст научной статьи К методике определения сопротивления материалов импульсному нагружению
Технологии изготовления деталей машиностроительных конструкций в основном основаны на пластическом деформировании материалов. Анализ условий работы материалов в конструкциях и при изготовлении деталей показывает на необходимость учета реономных (зависящих от времени) свойств материалов. Особенно это нужно учитывать при высокоскоростных нагружениях конструкций и технологиях штамповки и сварки взрывом, ковки и штамповки на автоматах.
Одной из основных задач экспериментальной механики деформируемого твердого тела является разработка методик для определения параметров, характеризующих пластическое деформирование материала. Обычно эти параметры определяют по экспериментальной зависимости напряжение-продольная деформация при испытаниях образцов в виде цилиндрических стержней при линейном напряженном состоянии растяжения или сжатия.
При импульсном нагружении (удар, взрыв), длительность фронта которого характеризуется микросекундами, необходимо учитывать, что напряженно-деформированное состояние стержня-образца создается упругопластическими волнами. В этом случае нужно определить зоны образца, где создается линейное напряженное состояние с равномерным распределением напряжений по поперечному сечению. На фронте волны практически невозможно создать однородное состояние по продольной координате и возникает задача синхронного определения напряжения и деформации в контрольном сечении образца.
Для определения зависимости напряжение-время, синхронной с деформацией, в ЮжноУральском государственном университете разработана оригинальная методика [1].
В отличие от принятых в мировой практике методик, рассмотренных в обзорных работах [2, 3] и известных нам по публикациям в периодической печати, по этой методике впервые удалось определить напряжения в контрольном сечении образца без предположений о виде уравнения состояния исследуемого материала и условий распространения волн в системе нагружения образца.
На схеме нагружения образца и установки датчиков (рис. 1) передающий стержень Т установлен на центрирующих резиновых втулках в стволе вертикальной пневмоустановки. Упругий прижим, не влияющий на распространение волны, обеспечивает контакт образца М со стержнем Т.
Импульс силы F(t). нагружающий систему, создастся ударом бойка, скорость которого обеспечивает упругое соударение. На расстоянии от точки удара более двух диаметров в стержне распространяется волна линейного напряженного состояния [4]. В работе [5] показано, что при этом напряжения равномерно распределены по поперечному сечению стержня. Упругая волна, распространяющаяся в стержне Т, при переходе границы Т-М создает в образце М упругопластическую волну. В работе [1] показано, что даже при притертых плоских контактных торцах стержней Т и М одинаковых диаметров D линейное напряженное состояние в образце формируется на расстоянии хо=О, 6D.
На основании уравнения движения элемента образца длиной dx
9F(x,t) 9v(x,t)
—-—- dx = рл (x) —-—- dx,(1)
ЭхSt сила в контрольном сечении
F(-W>p ^^is^dx,(2)
О/ где p и S(x) - плотность и площадь поперечного сечения недеформированного стержня, v(x,t) -массовая скорость, Со = д/^/р —скорость распространения упругого фронта волны, Е - модуль упругости.
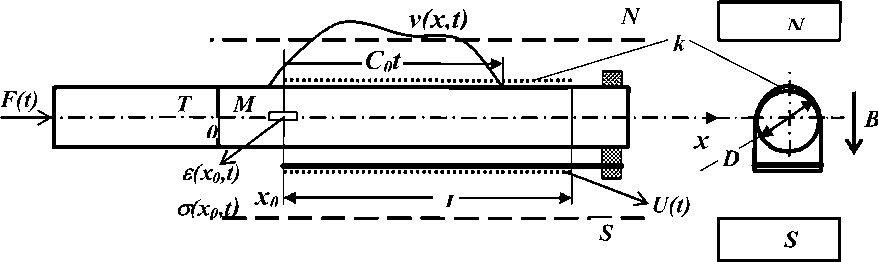
Рис. 1. Схемы нагружения образца М через стержень Т импульсом силы F(t) и установки датчиков для синхронного определения напряжения о(х0Д) и деформации £(х0Д) в контрольном сечении х0
Если при изготовлении образца площадь поперечного сечения в пределах его длины выдерживается с ошибкой не более 0,5 %, то можно принять S(x)=const.
По правилу дифференцирования интеграла по параметру (времени) имеем d Bv(x,t) . d^xp^)
— v(x, t) dx = ------- dx - v(C0Z, /)-------.(3)
dt Д Stdt
Учитывая, что v(Co4^=O, получим d
F(x0, t) = pS — f v(x, t)dx.
d,cl,
Для определения функции времени, представленной интегралом
J(xQ,t)- jv(x,0^9(5)
О/ разработан индукционный датчик [6], показанный на рис. 1.
Начиная от контрольного сечения х0, на образец намотана «виток к витку» однослойная катушка тонкого медного изолированного провода. Витки катушки к охватывают стержень и консольную планку, закрепленную на свободном конце образца. Часть каждого витка, примыкающая к образцу, приклеена к нему и движется со скоростью v(x,t) в поле постоянного магнита N-S. Участок, примыкающий к планке, неподвижен, а соединительные участки при движении не пересекают магнитный поток. Поэтому активная длина витка, в которой наводится ЭДС индукции, равна диаметру D образца. Длина магнита, в 1,5 раза большая длины катушки, и ширина, в 4 раза большая диаметра образца, обеспечивают неравномерность магнитного поля в пределах катушки датчика не более 1 %. Для сохранения однородности магнитного поля передающий стержень и образец изготовлены из немагнитных материалов. Сигнал ЭДС индукционного датчика
х0
J v(x,t)dx,
где В - магнитная индукция, и и L - количество витков и длина катушки датчика. На основании (4) и (6) сила в контрольном сечении
0 DBn dt условные напряжения
F(x0,t)
^о,0 = —~—•
Деформацию в контрольном сечении e(x0,t) определяют тензорезистором, база которого согласована с длиной фронта волны. Применение серийных фольговых тензорезисторов с базой 3 мм обеспечивает измерение деформаций до 5 %. В работе [7] показано, что для стержней из алюминия и стали (С0~5 мм/мкс) при длительности фронта импульса силы не менее 4 мкс, динамическая ошибка такого тензорезистора при определении максимального значения деформации в точке стержня, совпадающей с центром тензорезистора, не превышает 2 %. При определении немаксимального значения деформации на фронте и спаде импульса ошибка значительно меньше.
Если поперечным тензорезистором измерить поперечную деформацию, то можно определить фактическую площадь S(x^,t) и действительные напряжения
°/zOW) =
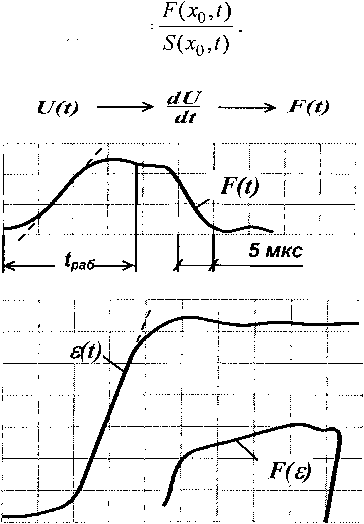
Рис. 2. Осциллограммы деформации e(t) и силы F(t) в контрольном сечении образца
На рис. 2 показаны типичные осциллограммы силы и деформации, полученные по данной методике и зарегистрированные на двух двухлучевых запоминающих аналоговых осциллографах С8-17.
Для получения сигнала F(t) сигнал индукционного датчика U(t) обрабатывали в дифференцирующем блоке dU/dt.
Один луч осциллографа регистрировал зависимость деформация-время s(x0,t). Второй луч в режиме X-Y одновременно регистрировал зависимость силадеформация F(e). Второй осциллограф регистрировал зависимость сила-время F (хоД), которую калибровали при упругом нагружении образца по сигналу F (x0,t)= e(xo,t)ES. Время регистрации силы ограничено длиной катушки датчика 1раб^Ь/С^.
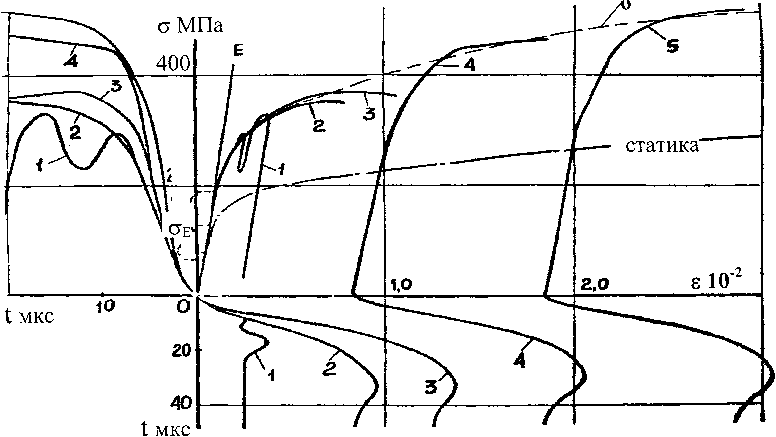
На рис. 3 приведены зависимости напряжение-деформация-время для алюминия АМц при сжатии стержней длиной 200 мм и диаметром 11,6 мм импульсами напряжений а(х0Д). Передающий стержень, таких же размеров как образец изготовлен из алюминия Д16Т с пределом пропорциональности 290 МПа. Для этих опытов tpa6=20 мкс. Там же показана статическая диаграмма сжатия образцов того же диаметра, высотой 20 мм.
Характерные закономерности процессов нагружения и деформирования проследим по рис. 3.
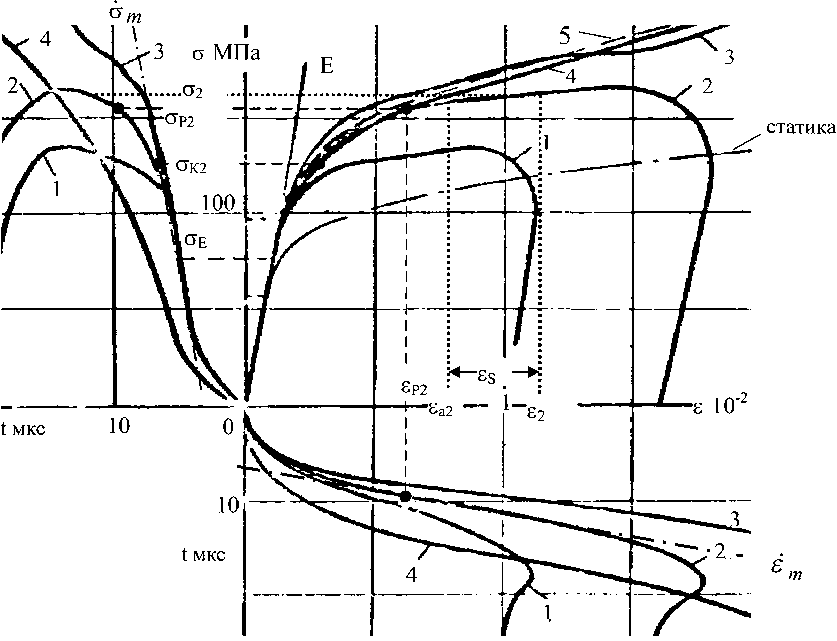
Рис. 3. Напряжение-деформация-время для алюминия АМц при режимах нагружения 1-4.
Зависимость 5 - среднее значение для семи образцов, испытанных по режиму 4
Зависимости напряжение-деформация определяли при четырех режимах нагружения j=l—4„ представленных осциллограммами напряжение-время. Соответствующие деформации представлены осциллограммами деформация-время. Штриховой линией 5 показана зависимость напряжение-деформация, осредненная по результатам испытаний 7 образцов в режиме нагружения 4.
Начальный режим нагружения характеризуется практически постоянной максимальной скоростью нагружения от , которая формируется при напряжениях, меньших предела пропорциональности с(1)<суе, и сохраняется при напряжениях, существенно превышающих предел пропорциональности. При испытаниях алюминия АМц реализовано дт = 3,3-107МПа/с . В этом режиме материал проходит два этапа деформирования, при которых увеличивается скорость деформации 8(7) > 0.
Первый этап - упругое деформирование г-о/Е, (10) ограниченное пределом пропорциональности сгЕ и характеризуемое модулем упругости Е.
В экспериментальной механике деформируемого твердого тела установлено, что для металлов и многих конструкционных материалов модуль упругости, определенный по результатам ультразвуковых измерений, практически совпадает со статическим значением. Наши измерения соответствуют этому результату.
Второй этап - пластическое деформирование, характеризующееся единой для всех режимов нагружения j=1-3 нелинейной зависимостью напряжение-деформация при действии напряжений °Е - °^Е - ^^j)- °Kj ■
Плавное уменьшение скорости нагружения относительно максимальной до значения
Gpj <д<дт
в интервале напряжений
cKj. < ^(tKj
В табл. 1 приведены скорости нагружения, реализованные при испытаниях алюминия АМц. В этих условиях для АМц dPj. > 0,4dw. Результаты аналогичного анализа: для алюминия АМгб dpj >0,156^ , для стали Х18Н1 ОТ QPj >0,36^ .
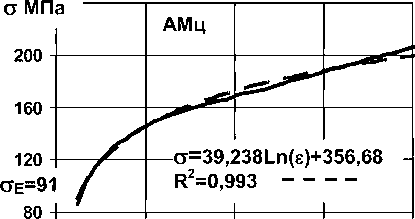
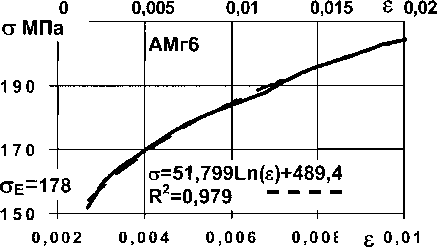
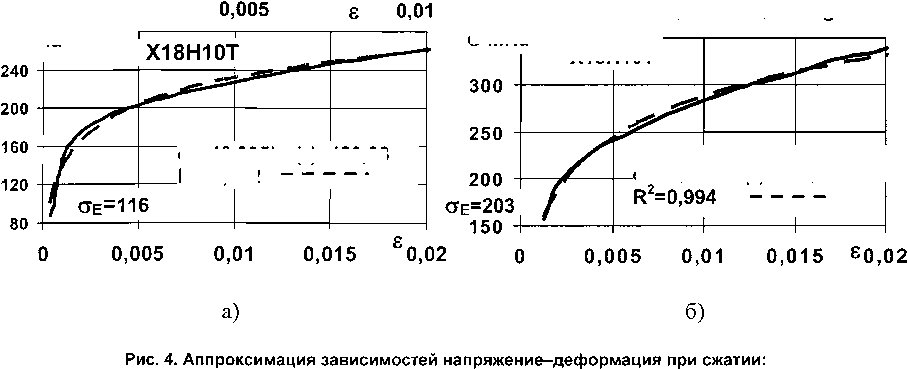
Пластические зависимости напряжение-деформация исследованных материалов при статическом (6^ < 1 МПа/с) сжатии (рис. 4, а) можно аппроксимировать уравнением а = ас h(s) + Ьс
(И)
1 2 > <тЕс - статический предел
, ^ ЕС где ас и Ьс - статические параметры материала, гЕС = —
Е пропорциональности.
Аналогичные зависимости получены при статическом растяжении нескольких марок конструкционных сталей.
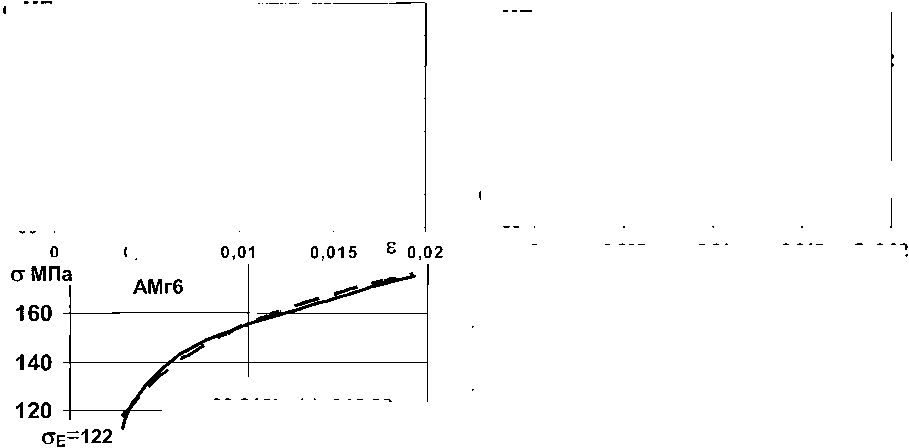
Qc=30,316Ln(8)+316,08
R2 =0.994
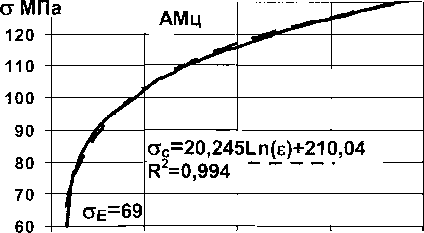
0,005
а МПа
Х18Н10Т
100 40
q МПа
o.=40,895Ln(8)+420,03 R-0,982
а - статика; б - скорость нагружения (3-9) 107 МПа/с
0=92,838Ln(e)+84O529
При импульсном нагружении (рис. 4, б) пластическую зависимость напряжение-деформация можно аппроксимировать аналогичным уравнением а = б/1п(8) + 6,
где а и Ъ - параметры материала при скорости нагружения др .
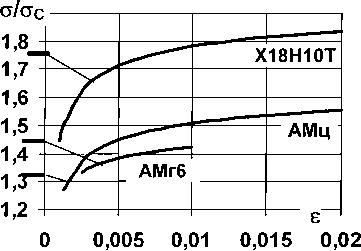
При пластическом деформировании в диапазоне напряжений аЕ < o(tE вующего конкретному режиму нагружения j=l—4. На основании (12) зависимость деформация-время еу(О = ехр v a > скорость деформации ёу(0 = о ДО (ajW-bA ——exp —--- a a соответст- В соответствии с условием аппроксимации aE < a < oPj максимальная скорость деформации Для алюминия АМц максимальные скорости деформации приведены в табл. 1. Деформация предела пропорциональности ее и параметры а и Ъ зависят от максимальной скорости нагружения су^ . Поэтому при пластическом деформировании зависимость напряже ние-деформация может быть описана уравнением /Д^еЛ,„) = 0- Напряжение aP. ограничивающее этап пластического деформирования, по физическому смыслу можно назвать пределом пластичности. На основании (11)и(12)с учетом (10) пределы пропорциональности при статическом и импульсном нагружениях определяем из уравнений: ^бс^сН^ес1 EVbc, (17) ge = aAn(cE /Е)л-Ь . (18) Таблица 1 Скорости нагружения и деформирования алюминия АМц Режим Нагружение Скорость нагружения, 106 МПа/с ^7Л03 1/с 6р 1 a 33 о > оР1 = O^j 4,5 U 2 О <0^-2 33 аХ2 - ст - °Р2 14 СУ > <3р2 3,6 1,9 3 а-°кз 33 aКЗ - a - °РЗ 8 су л сурз <8 2,8 4 о<сК4 20 °К4 ~ СТ - °Р4 8 СУ > СУ рд <8 1,9 Третий этап - деформирование при уменьшении скорости нагружения 0 < d(t) < др, происходит при напряжениях, больших предела пластичности, но не превышающих максимальное для заданного режима нагружения, cPj- < o(tPj Sy где tPj - время достижения напряжения GPj , увеличивается с постоянной максимальной скоростью 8^ (15), зависящей от режима нагружения. Для АМц в режиме 2 максимальная скорость деформации sw2 = 1,9 • 1031/с , т.е. сопротивление деформированию меньше, чем при пластическом деформировании. Как показано на рис. 3 (режим 2) общая деформация £2. вызванная напряжением <т2>(Ур2, равна сумме деформации 8а2, определяемой по уравнению (13), и дополнительной деформации 8S, зависящей от скорости нагружения 0 < а(/) < Gp . На основании (19) дополнительная деформация Ssj (0 = е7 (0 - еф = epj + smj (t - tPj) - exp где 8^- - exp '^2^? Для рассматриваемого примера j=2 и £S =^> Скорость дополнительной деформации При нагружении постоянным максимальным напряжением Gj (t>tM) = GMj = const a/Z > tMj) = 0 и дополнительная деформация является деформацией ползучести ^у (^м) = £pj + ^mj ^ -tpj)-6ХР ^м-Ь скорость которой равна гт] . Однако при этом вместо воздействия на материал повышенной температуры реализовано действие динамических напряжений, превышающих статические при заданной деформации. Поэтому дополнительную деформацию £S, можно назвать деформацией динамической ползучести. В работе [8] показана ползучесть стали при комнатной температуре при действии постоянных статических напряжений различного уровня. На основании (19) и (12) с учетом (15), (16) деформирование в режиме динамической ползучести может быть представлено уравнением Л(^Е^т^,?) = 0, где Gp При нагружении алюминия АМц по режиму 3 (рис. 3) на 8-й микросекунде произошло локальное резкое уменьшение скорости нагружения, которое отразилось локальной ползучестью. При увеличении скорости нагружения материал возвращается на пластическую зависимость напряжение-деформация. Четвертый этап деформирования - разгрузка. При разгрузке (а<сгм и G(t)< 0) деформация продолжает увеличиваться до максимального значения, но с уменьшающейся скоростью. При дальнейшем уменьшении напряжений происходит линейное уменьшение деформаций. Аналогичное явление ползучести при разгрузке было установлено в работе [9] при низких скоростях нагружения титанового сплава ВТ1-1. Полученные результаты испытаний образцов аустенитной стали Х18Н10Т. При режимах нагружения 2 и 3 выявили те же закономерности (рис. 5) пластического деформирования (динамической ползучести и разгрузки), что и при испытании образцов алюминия АМц, показанных на рис. 3. После нагружения по режиму 3 и разгрузки тот же образец был дважды испытан в режимах нагружения 4 и 5. При нагружении по режиму 4 увеличение напряжений до уровня сг3тах, с которого была проведена разгрузка режима 3, сопровождается упругим деформированием по уравнению (10). Но в этом случае предел пропорциональности сг£4«сг3тах. Дальнейшие пластическое деформирование, динамическая ползучесть и разгрузка происходят по законам первичного нагружения. Эти же явления имеют место и при нагружении по режиму 5 образца, испытанного в режимах 3 и 4. Ос-редненные результаты испытаний девяти образцов по этой программе, показанные пунктирной линией на рис. 5, соответствуют уравнению (12). При повторных нагружениях увеличиваются значения предела пропорциональности сг^ и предела пластичности о>, но сохраняются параметры уравнения (12). При о>оР проявляется ползучесть материала, как и при первом нагружении. Такая реакция металлов на повторное статическое нагружение известна как наклеп. При нагружении по режиму 1 в начале пластического деформирования была проведена частичная разгрузка с напряжения 1,8сге до напряжения 1,4о£ затем догрузка до 2,1 суе и полная разгрузка. Догрузка после частичной разгрузки продолжает процесс пластического деформирования. Следовательно, реакция материала на микросекундные изменения режима нагружения в виде наклепа такая же, как и при повторных нагружениях с интервалом в десятки минут. Рис. 5. Напряжение-деформация-время для стали Х18Н10Т при режимах нагружения 1-5. Линия 6 - среднее значение результатов испытаний 9 образцов Импульсные испытания стержневых образцов проводят в заданном режиме нагружения a(t), характерного для работы материала в конструкциях и при технологическом переделе. Деформация является реакцией материала на режим нагружения. Поэтому поведение материала обусловлено параметрами импульса напряжений: амплитудой, длительностью фронта, вершины и спада, скоростями нагружения и разгрузки. Параметры статического и импульсного нагружений испытанных материалов, осредненные по результатам испытаний 5-9 образцов, приведены в табл. 2. Наибольшее сопротивление материала импульсному деформированию - импульсное упрочнение реализуется на фронте импульса при максимальной скорости нагружения ат . На основании (12) и (11) импульсное упрочнение можно оценить отношением импульсного и статического напряжений, при которых реализуется одинаковая деформация 8>8Е, а aln(s) + Z? ос ас 1п(е) + Ьс На графиках импульсного упрочнения исследованных материалов (рис. 6) на оси ординат отмечены отношения импульсного и статического пределов пропорциональности Qe/gec (табл. 2). Рис. 6. Импульсное упрочнение а/стс для реализации деформации ^>8е Таблица 2 Параметры статического и импульсного нагружений испытанных материалов Материал АМц АМгб Х18Н10Т Е, 105МПа 0,724 0,723 1,94 Со? м/с 5100 5170 4950 р, 103кг/м3 2,78 2,68 7,92 Нагружение Статика Импульс Статика Импульс Статика Импульс 8 10'2* 2 1 2 а, МПа 20,245 39,238 30,316 51,799 40,895 92,838 Ь, МПа 210,04 356,68 316,08 489,4 420,03 840,29 R2 0,994 0,995 0,994 0,979 0,982 0,994 Не» МПа 69 91 122 178 116 203 ^Е^ЕС 1,32 1,46 1,75 £е, IO"2 0,095 0,13 0,17 0,25 0,06 0,1 dm, 106МПа/с 33 39 88 ^p/^m 0,24 0,16 0,3 8W, 1О31/С. 1,8 1,0 0,8 Диапазон логарифмической аппроксимации 8^ - 8max при 6т - ср Упрочнение алюминия АМц и стали Х18Н10Т интенсивно увеличивается до деформации 1%, затем при е>1,5% практически стабилизируется на уровне 1,55 и 1,85 соответственно. У алюминия АМгб импульсное упрочнение стабилизируется на уровне 1,42 при 6=1 %. Увеличение предела пропорциональности (ое/о£С>1) и импульсное упрочнение необходимо учитывать при разработке технологий обработки соответствующих материалов и при проектировании конструкций, работающих при волновом нагружении. Выводы 1. Применение разработанной методики синхронного определения напряжений и деформаций в контрольном сечении стержня-образца при распространении упругопластической волны обеспечивает детальное исследование процесса деформирования. 2. Экспериментально показано, что процесс деформирования зависит от напряжения и скорости нагружения. 3. Выявлены два последовательных вида деформирования: упругопластическое при постоянной максимальной скорости нагружения и динамическая ползучесть при уменьшении скорости нагружения и разгрузке. 4. Но применение методики ограничено возможностью испытаний только неферромагнитных материалов, которые не вносят искажения в равномерное магнитное поле индукционного датчика силы.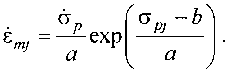
Список литературы К методике определения сопротивления материалов импульсному нагружению
- Купершляк-Юзефович Г.М. Методика измерения напряжений при импульсном нагружении стержня/Г.М. Купершляк-Юзефович, Ю.В. Шкербин//Проблемы прочности. -1981. -№ 1. -С. 41-45.
- Николас Т. Поведение материалов при высоких скоростях деформации/Т. Николас//Динамика удара: пер. с англ. -М.: Мир, 1985. -С. 198-256.
- Wang Li-Li. Influences of Stress Wave Propagation upon Studying Dynamic Response of Materials at High Strain Rates//Journal of Beijing Institute of Technology. -2004. -Vol. 13. -№ 3.
- Александров Е.В. Прикладная теория и расчеты ударных систем/Е.В. Александров, В.В. Соколинский. -М.: Наука, 1969. -200 с.
- Гольдсмит В. Удар и контактные явления при средних скоростях/В. Гольдсмит//Физика быстропротекающих процессов: сб. науч. тр. -М.: Мир, 1971. -Т. 2. -С. 153-201.
- A.c. 666447 (СССР). Датчик мгновенных значений механических напряжений в образце/Г.М. Купершляк-Юзефович, Ю.В. Шкербин. -Приоритет 19.04.1977; опубл. Б.И., 1979, № 21.
- Купершляк-Юзефович Г.М. Оценивание погрешностей измерения динамических деформаций тензорезисторами/Г.М. Купершляк-Юзефович//Датчики и системы. -2003. -№ 9. -С 8-11.
- Жуков A.M. Некоторые особенности поведения металлов при упругопластическом деформировании/A.M. Жуков//Вопросы теории пластичности: сб. науч. тр. -М.: Издательство АН СССР, 1961. -С. 30-57.
- Викторов В.В. Математическое и экспериментальное моделирование влияния временных и скоростных эффектов на механическое поведение материалов/В.В. Викторов, В.Н. Кукуджанов//Труды IX конференции по прочности и пластичности. -М.: Издательство РАН, 1996. -Т. 2. -С. 45-51.


